основы. 1. Общественное здоровье и здравоохранение как наука и предмет преподавания. Основные направления общественного здоровья и здравоохранения. Методы исследования и основные задачи
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
Приближенный метод оценки колеблемости вариационного ряда - определение лимита и амплитуды, однако не учитывают значений вариант внутри ряда. Основной общепринятой мерой колеблемости количественного приз- нака в пределах вариационного ряда является среднее квадратическое отклонение (σ - сигма). Чем больше среднее квадратическое отклонение, тем степень колеблемости данного ряда выше. Методикарасчетасреднегоквадратическогоотклонениявключаетследующиеэтапы: Находят среднюю арифметическую величину (Μ). Определяют отклонения отдельных вариант от средней арифметической (d=V-M). В медицинской статистике отклонения от средней обозначаются как d (deviate). Сумма всех отклонений равняется нулю. Возводят каждое отклонение в квадрат d2. Перемножают квадраты отклонений на соответствующие частоты d2*p. Находят сумму произведений ( d2*p) Вычисляют среднее квадратическое отклонение по формуле:  σ σ σ σ при n больше 30, или при n меньше либо равно 30, где n - число всех вариант.  Значениесреднегоквадратичногоотклонения: Значениесреднегоквадратичногоотклонения:Среднее квадратическое отклонение характеризует разброс вариант относительно средней величины (т.е. колеблемость вариационного ряда). Чем больше сигма, тем степень разнообразия данного ряда выше. Среднее квадратичное отклонение используется для сравнительной оценки степени соответствия средней арифметической величины тому вариационному ряду, для которого она вычислена. Вариации массовых явлений подчиняются закону нормального распределения. Кривая, отображающая это распределение, имеет вид плавной колоколообразной симметричной кривой (кривая Гаусса). Согласно теории вероятности в явлениях, подчиняющихся закону нормального распределения, между значениями средней арифметической и среднего квадратического отклонения существует строгая математическая зависимость. Теоретическое распределение вариант в однородном вариационном ряду подчиняется правилу трех сигм. Если в системе прямоугольных координат на оси абсцисс отложить значения количественного признака (варианты), а на оси ординат - частоты встречаемости вариант в вариационном ряду, то по сторонам от средней арифметической равномерно располагаются варианты с большими и меньшими значениями. Установлено, что при нормальном распределении признака: 68,3% значений вариант находится в пределах М1 95,5% значений вариант находится в пределах М2 99,7% значений вариант находится в пределах М3 Среднее квадратическое отлонение позволяет установить значения нормы для клинико-биологических показателей. В медицине интервал М1 обычно принимается за пределы нормы для изучаемого явления. Отклонение оцениваемой величины от средней арифметической больше, чем на 1 указывает на отклонение изучаемого параметра от нормы. В медицине правило трех сигм применяется в педиатрии для индивидуальной оценки уровня физического развития детей (метод сигмальных отклонений), для разработки стандартов детской одежды Среднее квадратическое отклонение необходимо для характеристики степени разнообразия изучаемого признака и вычисления ошибки средней арифметической величины. Величина среднего квадратического отклонения обычно используется для сравнения колеблемости однотипных рядов. Если сравниваются два ряда с разными признаками (рост и масса тела, средняя длительность лечения в стационаре и больничная летальность и т.д.), то непосредственное сопоставление размеров сигм невозможно, т.к. среднеквадратическое отклонение - именованная величина, выраженная в абсолютных числах. В этих случаях применяют коэффициент вариации (Cv), представляющий собой относительную величину: процентное отноше- ние среднего квадратического отклонения к средней арифметической. Коэффициент вариации вычисляется по формуле: С 100 v М Чем выше коэффициент вариации, тем большая изменчивость данного ряда. Считают, что коэффициент вариации свыше 30 % свидетельствует о качественной неоднородности совокупности. 30.Коэффициент вариации. Методика расчета, анализ. Вариация — различие значений какого-либо признака у разных единиц совокупности за один и тот же промежуток времени. Причиной возникновения вариации являются различные условия существования разных единиц совокупности. Вариация — необходимое условие существования и развития массовых явлений.Определение вариации необходимо при организации выборочного наблюдения, статистическом моделировании и планировании экспертных опросов. По степени вариации можно судить об однородности совокупности, устойчивости значений признака, типичности средней, о взаимосвязи между какими-либо признаками. Коэффициент вариации (Cv) определяет изменчивость вариационного ряда в процентах и дает возможность судить о качественной однородности изучаемой совокупности. Коэффициент вариации является относительной мерой разнообразия, так как исчисляется как процентное отношение среднеквадратического отклонения (σ) к средней арифметической величине (M). Формула коэффициента вариации выглядит следующим образом: Cv= Для ориентировочной оценки степени разнообразия признака пользуются следующими градациями коэффициента вариации. Если коэффициент составляет более 20 %, то отмечают сильное разнообразие; при 20-10 % - среднее, и если коэффициент менее 10 %, то считают, что разнообразие слабое. Коэффициент вариации применяют при сравнении степени разнообразия признаков, имеющих различия в величине признаков или неодинаковую их размерность. 31.Методы оценки достоверности результатов статистических исследований. В практической и научно-практической работе врачи обобщают результаты, полученные, как правило, на выборочных совокупностях. Для более широкого распространения и применения полученных при изучении репрезентативной выборочной совокупности данных и выводов надо уметь по части явления судить о явлении и его закономерностях в целом. Учитывая, как правило, что врачи проводят исследования на выборочных совокупностях, теория статистики позволяет с помощью математического аппарата (формул) переносить данные с выборочного исследования на генеральную совокупность. При этом врач должен уметь не только пользоваться математическими формулами, но и делать выводы, соответствующие каждому способу оценки достоверности полученных данных. С этой целью врач должен знать способы оценки достоверности. В статистических исследованиях применяются 2 вида наблюдений - сплошное и выборочное. Самые надежные результаты можно получить при применении сплошного метода, т.е. при изучении генеральной совокупности. Между тем изучение генеральной совокупности связано со значительной трудоемкостью. Поэтому в медико-биологических исследованиях, как правило, проводятся выборочные наблюдения. С тем, чтобы полученные при изучении выборочной совокупности данные можно было перенести на генеральную совокупность, необходимо провести оценку достоверности результатов статистического исследования. Выборочная совокупность может недостаточно полно представлять генеральную совокупность, поэтому выборочным наблюдениям всегда сопутствуют ошибки репрезентативности. По размерам средней ошибки ( m ) можно судить, насколько найденная выборочная средняя величина отличается от средней генеральной совокупности. Малая ошибка указывает на близость этих показателей, большая ошибка такой уверенности не дает. На величину средней ошибки средней арифметической влияют следующие два обстоятельства: однородность собранного материала чем меньше разбросанность вариант вокруг своей средней, тем меньше ошибка репрезентативности. число наблюдений средняя ошибка будет тем меньше, чем больше число наблюдений. Средняя ошибка средней арифметической вычисляется по формуле: Средняя ошибка для относительных величин вычисляется по формуле: Р - величина показателя в расчете на 100, 1000, 10 000 и т.д. q - разность между основанием, на которое рассчитывается показатель, и его конкретным числовым значением (100 - Р, 1000 - Р, 10 000 - Р и т.д.). При n < 30 в знаменателе n - 1. Пример 8. Средний рост восьмилетних мальчиков составил - 125,5 см, среднее квадратическое отклонение =±3,4 см , n=73 mм= ± =±0,4 см Пример 9. +Численность детей в возрасте до года по данным детской поликлиники составила 450 ,из них ни разу не болели 100 детей. Необходимо определить "Индекс здоровья" (процент ни разу не болевших детей) и вычислить ошибку для данного показателя. Индекс здоровья 32.Оценка достоверности разности средних и относительных величин. Методика расчета. При оценке достоверности средних или относительных величин руководствуются следующим правилом:средняя арифметическая или относительная величина при числе наблюдений в выборочной совокупности 30 и более должны превышать свою ошибку не менее чем в 2 раза. В рассматриваемых примерах средняя арифметическая, характеризующая рост восьмилетних мальчиков и показатель „индекс здоровья” превышают свои ошибки соответственно: Высказанное положение вытекает из теории «вероятности», под которой понимается числовая мера объективной возможности появления случайного события. Вероятность - число, которое находится между 0 и 1, или между 0% и 100%. Математиками определено, что той или иной вероятности, выраженной в процентах, соответствует определенное значение критерия t Стьюдента. Так, например, вероятности равной Р = 68,3% соответствует t= 1,0, вероятности равной Р = 95,5 % соответствует t = 2,0 вероятности равной Р = 99,7 % соответствует t = 3,0 . В медико-биологических исследованиях событие является статистически достоверным, если вероятность его появления соответствует значению критерия t Стьюдента, равное 2. Средняя ошибка позволяет не только оценить достоверность относительного показателя или средней величины, но и найти доверительные границы средней величины или относительного показателя в генеральной совокупности М ген.= М выб. ± t Р ген. = Р выб . ± t Как уже было сказано, величина средней ошибки указывает, насколько средняя величина и относительный показатель выборочной совокупности отличаются от соответствующих величин в генеральной совокупности. Величина t*m является тем доверительным интервалом по отношению к средней или относительной величине, в котором с определенной степенью вероятности можно ожидать нахождение средней или относительной величины в генеральной совокупности. Пример 10. М выб .= 125,5 см; m = ± 0,4 см. При 95% вероятности t =2, при 99,7 % - t = 3 . М ген.= 125,5 см ± 2 М ген.= 125,5 см ± 3 Таким образом, с вероятностью 95% можно ожидать, что средняя будет находиться в пределах от 124,7 до 126,3 см и с вероятностью 99,7% - в пределах от 124,3 до 126,7 см. +Понятно, что действительное значение средней можно получить только при обследовании всех 8-летних мальчиков, но как это очевидно из полученных данных, подобное исследование нецелесообразно, т.к. средняя арифметическая статистически достоверна (Р > 99,7%), а доверительный интервал для средней в генеральной совокупности является весьма незначительным -t 33.Коэффициент Стъюдента. Методика расчета. Практическое значение для оценки результатов исследования. Метод Стьюдента применим для сравнения выборок, отдельные наблюдения в которых распределены нормально. Для оценки различий двух сравниваемых выборок методом Стьюдента необходимо предварительно определить некоторые статистические параметры этих выборок. Поэтому метод называют параметрическим. Критерий Стьюдента (t) может использоваться для оценки достоверности различия двух средних величин как в независимых (несвязанных), так и в зависимых (связанных) группах. С целью проверки высказанных гипотез применяются различные статистические приемы, среди которых наиболее простым является следующий: 34.Измерение связи между явлениями и признаками. Корреляция: ее виды, методика расчета. Различают две формы (вида) связи:1)функциональная связь–имеет строгую зависимость явлений, чем больше радиус, тем больше длина окружности (2ПR) и эта зависимость проявляется в каждом конкретном случае: изменение одного признака(явления) вызывает обязательно строго определенные изменения другого признака (явления), часто установлена их взаимосвязь математически; 2)корреляционная связь–не имеет строгой зависимости и не проявляется в каждом конкретном случае, а только при массовомсопоставлении изучаемых явлений. Такой вид связи характерен для социально-гигиенических процессов, клинической медицины и биологии. Например, вес человека зависит в основном от его роста, но влияют также на вес и другие факторы: питание, затраты сил на работу, состояние здоровья. Поэтому у лиц одинакового роста, обычно вес варьируется в определенных пределах.В свою очередь корреляционная связь может быть:–прямолинейной, когда отмечается относительно равномерное изменение средних значений одного признака при равных изменениях другого (соответствие между изменениями систолического и диастолического давления);–криволинейной, когда при равномерном изменении одного признака могут наблюдаться возрастающие или убывающие значения другого признака.Кроме того, связьмежду признаками различается по направлению. Так, когда изменение одного явления ведет к изменению другого явления в том же направлении, (рост экономической обеспеченности ведет к улучшению питания населения) отмечается прямая (положительная) связьи наоборот, когда явления изменяются в разных направлениях (снижение заболеваемости полиомиелитом при увеличении числа привитых) говорят об обратной (отрицательной) связи.Закономерность корреляционной связи пробивается через случайность при массовых наблюдениях. И изучается она статистическими методами –вычислением коэффициентов корреляции 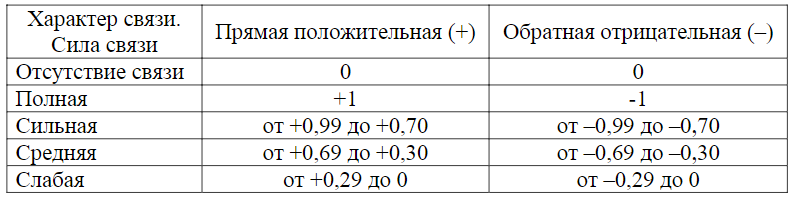 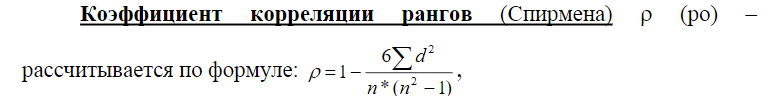 где 6 –постоянный коэффициент,n –число коррелируемых пар,d –разность рангов (между порядковыми номерами рядов), Σ –знак суммы.Условиями использования коэффициента ранговой корреляцииявляются:1)небольшое число коррелируемых пар;2)нет необходимости в точных результатах;3)признаки имеют не только количественные, но и атрибутивные значения (описательные).Методика вычисления коэффициента ранговой корреляции:I этап –присвоение рангов (порядковых номеров) по каждому ряду числовых значений признака. При наличии нескольких одинаковых значений изучаемого признака, ранги присваиваются одни и те же и соответствуют они средней их порядковых номеров. II этап –вычисление разности между рангами в каждой паре коррелируемых признаков. III этап –рассчитывается квадрат разности рангов и определяется их сумма. IV этап –рассчитывают коэффициент ранговой корреляции. Пример:Измерение корреляции между смертностью от рака молочной железы и от рака шейки матки методом рангов (на 100000 женщинв 5 районах) 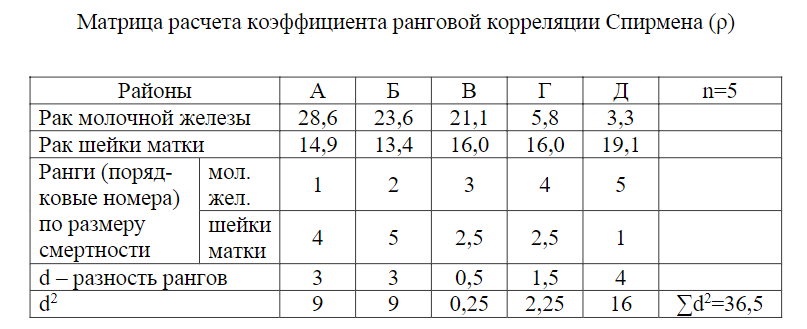 При присвоении рангов (в примере от большей смертности к меньшей) при одинаковых величинах явления в ряду, ранги берутся в среднем из суммы их очередных порядковых номеров. Так 19,1 –1 ранг, 16,0 –2-ой, следующий тоже 16,0 –3-ий, так как значения одинаковые, берем: (2+3)/2=5/2=2,5 и каждому одинаковому уровню присваиваются одинаковые ранги равные среднему значению. В нашем примере –2,5.По выше приведенной формуле вычисляем коэффициент рангов: 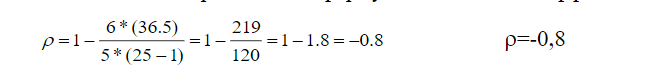 Для определения достоверности коэффициента корреляции рангов вычисляется его ошибка по формуле:  35.Расчет коэффициента корреляции по методу квадратов (Пирсона). Практическое применение. 36. Расчет коэффициента корреляции по методу ранговой корреляции (Спирмена). Практическое значение. |
