Курсовая. 1 Описание системы терморегулирования
 Скачать 1.99 Mb.
|
|
2.4 Расчет параметров цепи, задающей напряжение Напряжение  задает цепь  . Для того, чтобы регулировать в пределах от 0 до 10 В, необходимо разбить резистор  на постоянный  и переменный  . Тогда .Принимая ток  мА, по закону Ома определяем кОм, кОм, кОм.Из ряда стандартных сопротивлений Е24 выбираем  кОм;  кОм;  кОм [3].2.5 Расчёт параметров сравнивающего усилителя У2 Операционный усилитель У2 сравнивает  с  . Коэффициент усиления , .Из ряда стандартных сопротивлений Е24 выбираем  кОм [3]. Следовательно, кОм.Из ряда стандартных сопротивлений Е24 выбираем  кОм [3].2.6 Расчет параметров сумматора У3 Сумматор У3 служит для суммирования сигналов, которые поступают с интегрального и пропорционального каналов.  .Коэффициент усиления  , поэтому из ряда стандартных сопротивлений Е24 выбираем  кОм [3].3 Математическая модель системы терморегулирования 3.1 Функциональная схема При построении математической модели исследуемой системы используется структурный метод. В соответствии с этим методом исходная принципиальная схема заменяется упрощённой функциональной схемой, представленной на рисунке 2. 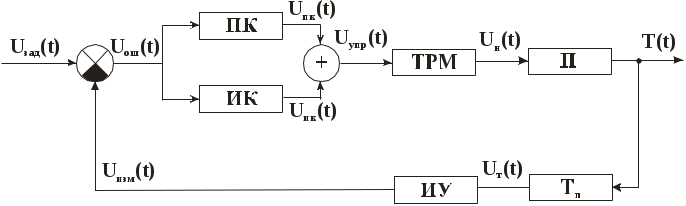 Рисунок 2 - Функциональная схема системы терморегулированиягде ПК – пропорциональный канал, ИК – интегральный канал, ТРМ – тиристорный регулятор мощности, П – электрическая печь, ИУ – измерительный усилитель, Тп – термопара,  – напряжение заданное, – напряжение ошибки, – напряжение на пропорциональном канале, – напряжение на интегральном канале, – управляющее воздействие на ТРМ, – управляющее воздействие на печь, – сигнал термопары, – напряжение измерительного устройства.3.2 Описание функциональных элементов передаточными функциями 3.2.1 Электрическая печь Для нагревательного объекта, в качестве которого выступает электрическая печь, исходным является уравнение теплового баланса  ,где  - теплоемкость объекта, - теплоотдача объекта, - температура, - подводимая к объекту тепловая энергия [1].Поделив обе части на , получим ,или, переходя к операторной форме записи, запишем следующее уравнение  ,где  - постоянная времени объекта, - коэффициент передачи. Следовательно, передаточная функция электрической печи  ,и поэтому нагревательный объект можно представить инерционным типовым звеном. Рассчитаем параметры  и  . .Из исходных данных таблице 1 известно, что изменение напряжения питания электрической печи  В ведет к изменению температуры печи на  . Следовательно, значение коэффициента передачи печи  .Так как печь описывается типовым инерционным звеном, то уровня 95% от установившегося значения переходный процесс достигает за время  , т.е. , ,где  - время разогрева печи до номинальной температуры.Из исходных данных таблице 1  ч. Подставив числовые значение получим с.Подставив найденные параметры и , передаточная функция электрической печи .3.2.2 Тиристорный регулятор мощности Так как тиристорный регулятор мощности является быстродействующей электрической схемой, то не стоит учитывать его динамические свойства, т.е.  . (1)Из исходных данных таблице 1  В, входной сигнал  В. Следовательно, .Запишем уравнение (1) в операторной форме  .Тогда, передаточная функция тиристорного регулятора мощности  , .Т.е. тиристорный регулятор мощности можно представить усилительным типовым звеном. 3.2.3 Термопара Термопара служит для измерения температуры и преобразует изменение температуры в термоЭДС. Конструктивно термопара выполняется в виде достаточно массивного стержня, при помещении которого в зону измерения требуется определенное время для его прогрева до температуры окружающей среды. Следовательно, результат измерения будет получен не мгновенно, а с некоторой задержкой [1]. Нагрев тела термопары опишем уравнением теплового баланса  , (2)где  - теплоемкость тела термопары, - теплоотдача тела термопары, - измеряемая температура, - температура тела термопары.Преобразование температуры в термоЭДС опишем приближенной зависимостью  ,где  - термоЭДС.Из полученного уравнения выразим  .Тогда уравнение 2 примет вид  ,или, переходя к операторной форме записи,  ,где  - постоянная времени термопары, - коэффициент преобразования термопары.Следовательно, передаточная функция для термопары  ,т.е. термопару можно представить инерционным типовым звеном. - показатель тепловой инерционности. Из исходных данных таблицы 2 для термопары ТХК 9312  с. Для нахождения  воспользуемся градуировочной характеристикой термопары  ХК(L) [2]. Рабочая температура  (исходные данные таблица 1), тогда , , мВ [2], мВ [2], .Тогда, передаточная функция для термопары  .3.2.4 Измерительный электронный усилитель У1 Измерительный электронный усилитель У1 служит для усиления сигнала получаемого от термопары и является быстродействующим устройством, поэтому его инерционные свойства практически не сказываются на динамике системы. Рабочий участок характеристики преобразования У1 является линейным, тогда уравнение для У1 будет иметь следующий вид  .Возьмем  В, из исходных данных таблицы 1  , тогда,  мВ [2]. .Передаточная функция электронного усилителя У1 примет вид  , .Т.е. измерительный электронный усилитель У1 можно представить усилительным типовым звеном. 3.2.5 Пропорциональный – интегральный регулятор 3.2.5.1 Интегральный канал регулятора Схема интегрального канала представлена на рисунке 3. Усилитель У5 считаем идеальным, т.е. 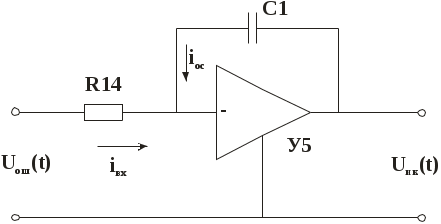 . Рисунок 3 – Схема интегрального канала регулятора Используя законы Кирхгофа и Ома, находим   , (3) , ,где  - входной ток, - ток обратной связи.Дифференцируя данное уравнение по  , получаем , .Подставляем найденные и в уравнение 3 , , , ,где  - коэффициент передачи.Запишем полученное уравнение в операторной форме записи  .Тогда, передаточная функция интегрального канала регулятора  .Т.е. интегральный канал регулятора можно представить интегрирующим типовым звеном. |