Курсовая. 1 Описание системы терморегулирования
 Скачать 1.99 Mb.
|
|
4.3 Передаточная функция системы терморегулирования с настроенным регулятором Передаточная функция разомкнутой системы  .Тогда передаточная функция замкнутой системы примет вид  .Характеристический полином замкнутой системы  .5 Исследование устойчивости системы терморегулирования 5.1 Оценка устойчивости при помощи алгебраического критерия устойчивости Гурвица При исследовании устойчивости системы с использованием алгебраического критерия устойчивости Гурвица рассматривается характеристический полином замкнутой системы. По Гурвицу для устойчивой системы должны соблюдаться два условия: коэффициенты характеристического полинома должны быть положительными; должны быть положительными определители, составленные из этих коэффициентов [1]. Характеристический полином замкнутой системы .1)  ,  , , .2)Для системы третьего порядка  Оба условия критерия выполняются, следовательно, данная система устойчива. 5.2 Построение области устойчивости системы методом D-разбиения Область устойчивости строится в плоскости двух задаваемых параметров системы  и  . Для выполнения исследования необходимо найти характеристический комплекс системы. Запишем характеристический полином замкнутой системы  , .Так как  и  , то  .Тогда, подставив числовые значения,  , .Преобразуем последнее выражение в характеристический комплекс, для этого вместо 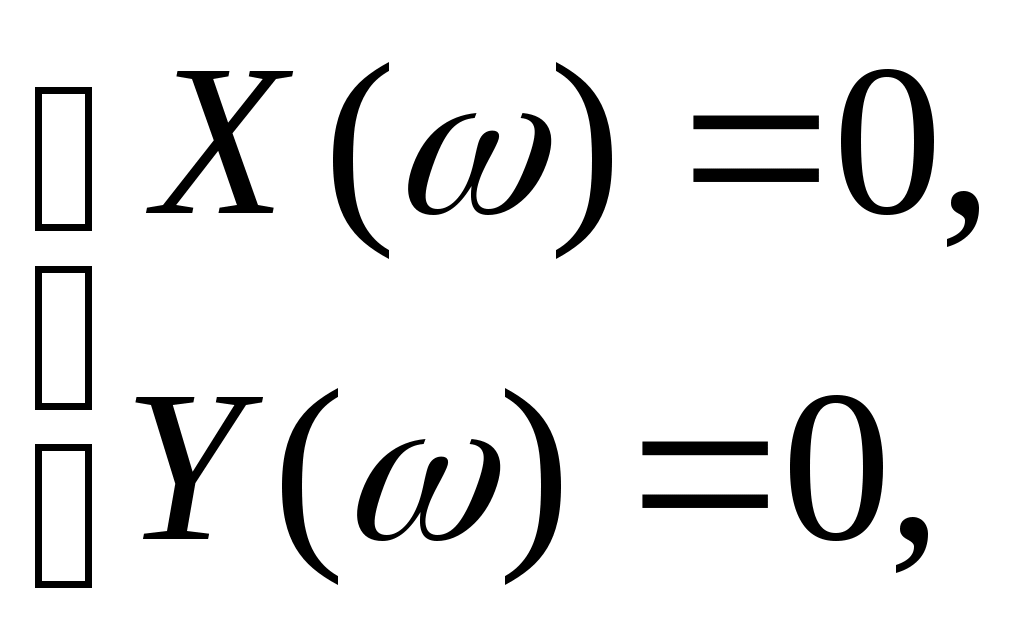 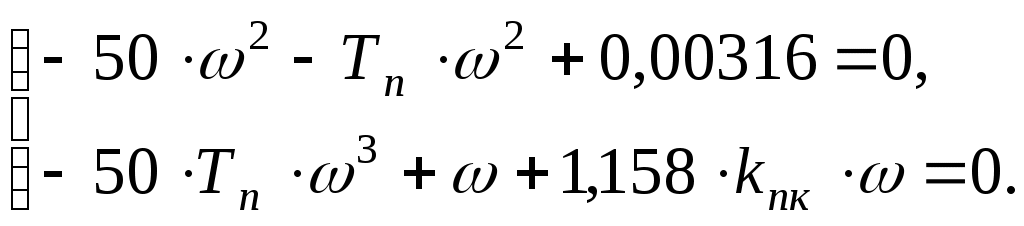подставим   Найдем параметрические уравнения границы устойчивости  Выразим 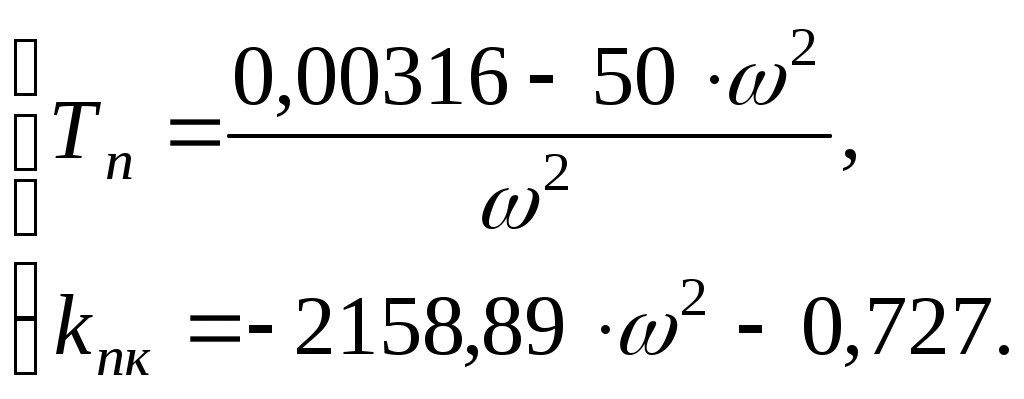и : Выражения в полученной системе являются параметрическими уравнениями границы устойчивости. Исследуем ход кривой, выявив ее особые точки. Характерными точками прямой являются точки разрыва и точки пересечения ее осей координат [1]. Найдем точки разрыва:  ,  .Найдем точки пересечения осей координат:  , т.е.  при  кривая пересекает ось , кривая не пересекает ось .Задаем ряд значений частоты  в пределах  . Так как частота входит в параметрические выражения границы области устойчивости в четной степени, то достаточно рассмотреть только область положительных частот  . Зависимости  и  отображены в таблице 6.Таблица 6
Определяем дополнительные границы области устойчивости приравниванием к нулю первого коэффициента характеристического многочлена и его свободного члена [1]:  Определяем расположение области устойчивости относительно границ с использованием правила штриховки. Для этого составляем определитель вида [1] 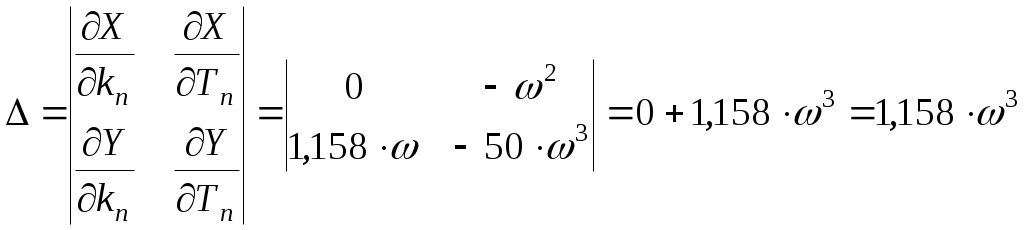 .Исследуем знак определителя. Если  , то  двигаясь в направлении  , область штрихуется справа, а если  , то  двигаясь в направлении , область штрихуется слева.График области устойчивости системы представлен на рисунке 9. Проверяем настроенную систему терморегулирования с помощью контрольной точки A(  ). Точка A(16,7; 6144) попадает в построенную область устойчивости.6 Анализ качества системы 6.1 Анализ качества системы по логарифмическим частотным характеристикам Оцениваем ЛЧХ системы по рисунку 8.  Чтобы система обладала достаточным качеством, запас устойчивости по фазе должен быть не менее  , а запас по амплитуде должен быть не менее  .Запас устойчивости по фазе  .Запас устойчивости по амплитуде  .Длительность переходного процесса  , .6.2 Анализ качества переходного процесса Для составления уравнения переходного процесса необходимо воспользоваться передаточной функцией замкнутой системы  .Следовательно, 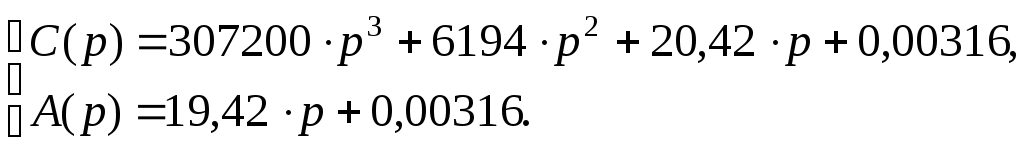  ,или, подставив значения,  (5)Структурная схема замкнутой системы представлена на рисунке 10.  Рисунок 10 – Структурная схема замкнутой системы Для того, чтобы построить график переходного процесса, необходимо решить дифференциальное уравнение численным методом (методом Рунге-Кутты). Для этого разбиваем передаточную функцию на две составляющие как показано на рисунке 11. 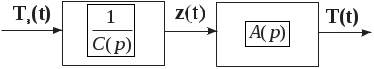 Рисунок 11 – Преобразованная структурная схема замкнутой системы Получаем новую систему уравнений 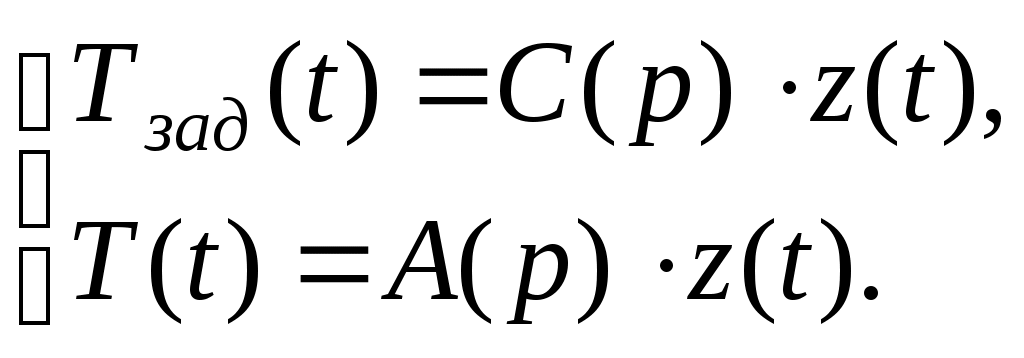 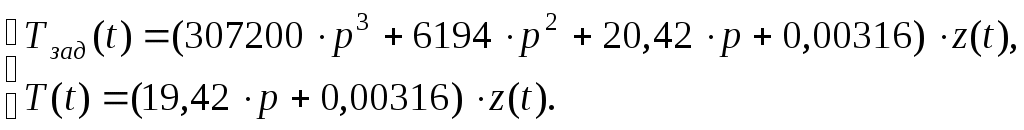 Записываем уравнение 5 в нормальной форме Коши 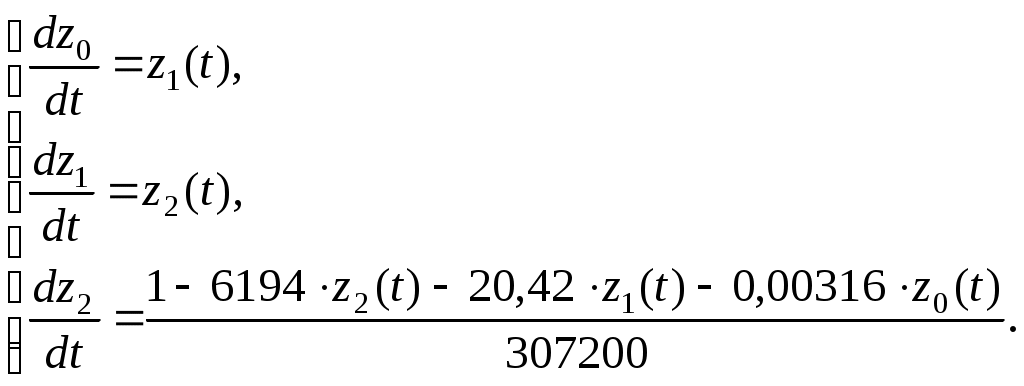 .Итоговое решение находим по формуле  .Для решения дифференциального уравнения и построения графика переходного процесса воспользуемся программой MathCAD 2000 Professional. Задаем: начальные условия равны нулю, максимальное время переходного процесса 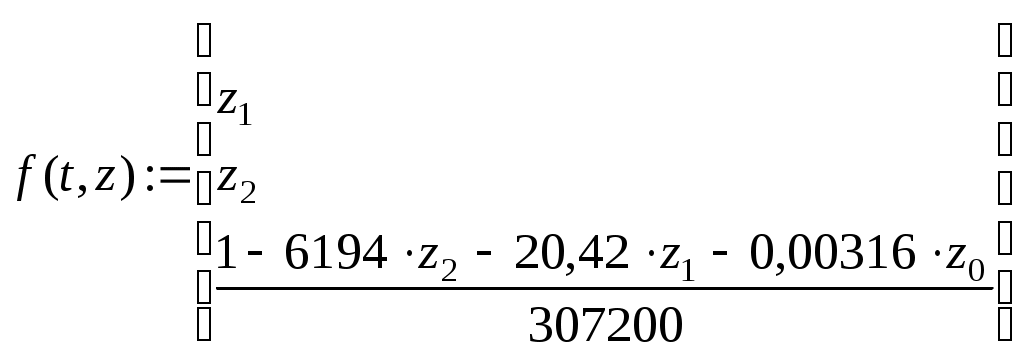 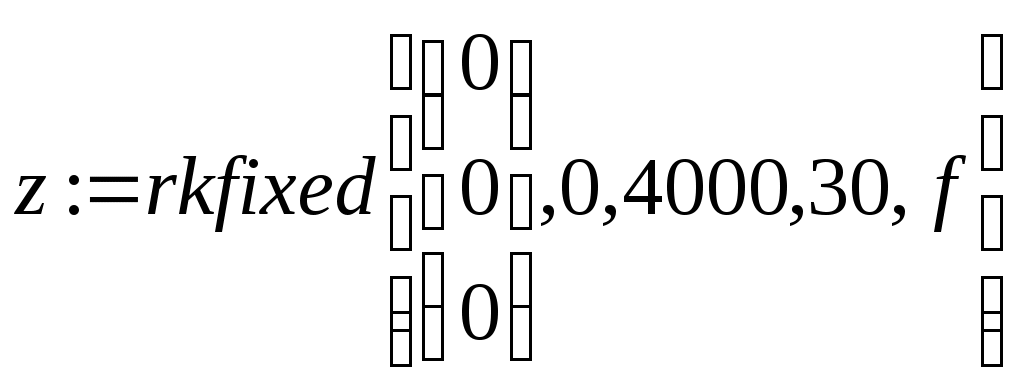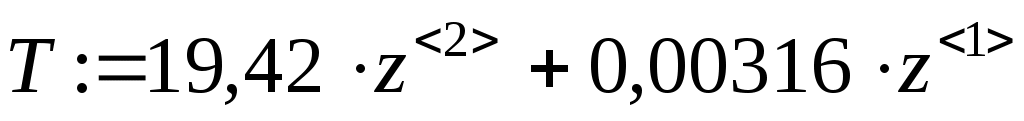с, количество точек  . , , .Значения функций  и  представлены в таблицах 7 и 8 соответственно.Таблица 7
Таблица 8
График переходного процесса представлен на рисунке 12. 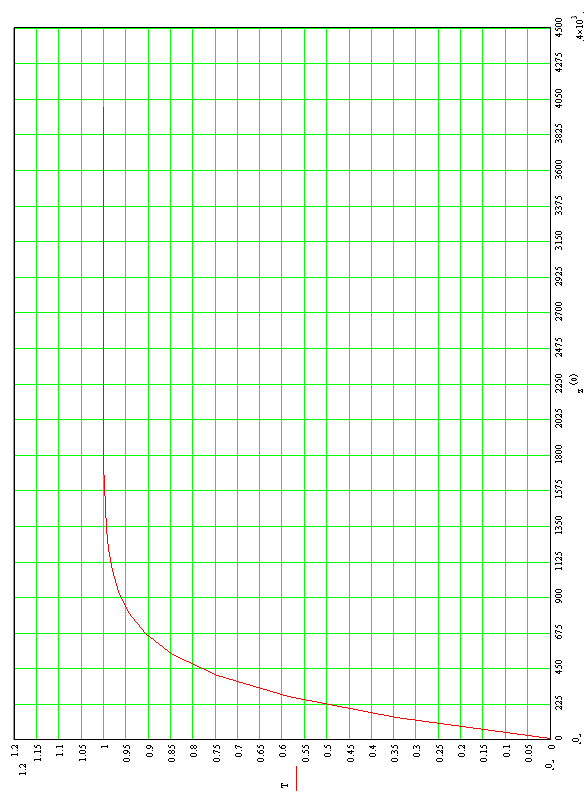  По графику можно увидеть, что система имеет плавный апериодический процесс, отсутствует перерегулирование. Длительность переходного процесса  с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
