3)1.определитель не изменится если его строки заменить его же столбцы
2.при перестановки любых 2х строк и столбцов соответственно определитель меняет знак на противоположный сохраняя абсолютное значение
3. если определитель содержит строку или столбец целых состоящих из 0 то такой определитель равен 0
4. если определитель содержит 2 одинаковые строки и 2 одинаковых столбца та такой опред =0
5. общий множитель элементов строки и столбца можно выность за знак определителя
6. если определитель содержит две пропорциональные строки или два пропорц столбца то такой опред=0
7. если к элементам строки или столбца опред прибавить элементы другой строки или столбца соответ умножить на одно и тоже число опред не изменится
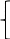4) Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
a11⋅x1+a12⋅x2+…+a1n⋅xn=b1
a21⋅x1+a22⋅x2+…+a2n⋅xn=b2
……………………………………..
am1⋅x1+am2⋅x2+…+amn⋅xn=bm
Упорядоченный набор значений
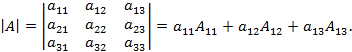
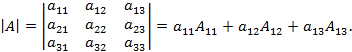Расширенной матрицей системы A=(A∣B)
называется матрица, полученная из матрицы системы A
, дописыванием справа после вертикальной черты столбца свободных членов.основная матрица теорема кранекера карпелли Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы.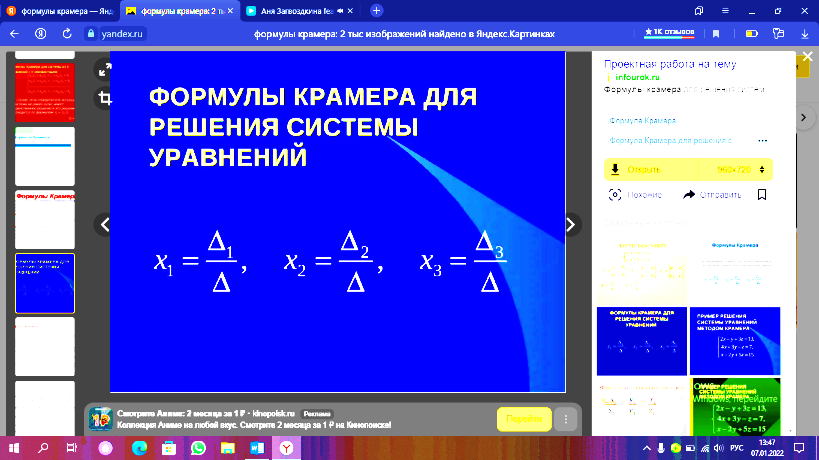
5) Ме́тод Га́усса —Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы6) формулы крамера
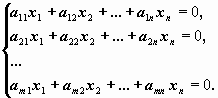7) Однородной системой линейных уравненийназывается система, правая часть которой равна нулю:
Матричный вид однородной системы:
Ax=0.
Однородная система в с е г д а с о в м е с т н а, поскольку любая однородная линейная система имеет по крайней мере одно решение:
x1=0 , x2=0 , ..., xn=0.Если
однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется
тривиально совместной. Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называется
нетривиально совместной.Доказано, что при
m=n для нетривиальной совместности системы
необходимо и достаточно, чтобы
определитель матрицы системы был равен нулю.
Справедливо следующее утверждение.
Для того, чтобы однородная система была нетривиально совместна, необходимо и достаточно, чтобы ранг
r матрицы системы был меньше числа неизвестных
n.
8) Определение: Матрицей называется таблица чисел (выражений), имеющая m строк и n столбцов: Если m ≠ n, то матрицу называют прямоугольной. Если m = n, то матрицу называют квадратной, порядка n. Элементы, из которых составлена матрица, называются элементами матрицы Некоторые частные случаи матриц 1. m*1 называют матрицей –столбцом m 2) 1 × n называют матрицей -строкой длины n . 3) Нулевой матрицей
Единичной
матрицей называется диагональная матрица, у которой все элементы главной диагонали равны единице. Единичную матрицу обычно обозначают латинской буквой E:
Опр. Матрица, все элементы которой равны нулю, называется нулевой и обозначается латинской буквой O.
Опр. Квадратная матрица, все элементы которой расположенные по одну сторону от главной диагонали, равны нулю, называется треугольной. Верхняя треуголҗна и ниңняя теруголҗная
Опр. Матрица называется ступенчатой, если для любой ее строки выполнено следующее условие: под первым слева ненулевым элементом строки и предшествующими ему нулевыми элементами этой строки все элементы матрицы равны нулю.
Действия над матрицами
1. Суммой (разностью) двух матриц
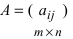
и
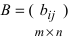
одинаковой структуры называется матрица той же размерности
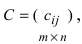
элементы которой вычисляются по формуле:
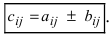2. При умножении вещественного числа k на матрицу 
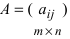все элементы матрицы умножаются на это число.3. Произведением матриц 
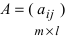и 
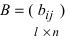называется матрица 
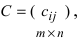элементы которой вычисляются по формуле: 
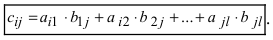Определение: Обратной матрицей к исходной квадратной матрице
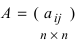
называется матрица
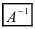
той же структуры, произведение которой с матрицей
А коммутативно и равно единичной матрице, то есть
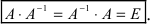
Рассмотрим
схему построения обратной матрицы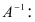 
находят детерминант матрицы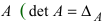 
- определитель матрицы А , если 
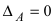, то обратной матрицы не существует);
вычисляют алгебраические дополнения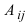 
всех элементов определителя 
;
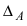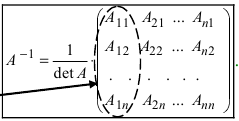
записывают выражение для обратной матрицы
Замечание: Обращаем
внимание на то, что
матрица алгебраических дополнений записана в транспонированном виде.9) Вектор – это
направленный отрезок прямой, т. е. отрезок, имеющий определенную длину и определенное направление. Нулевой вектор длина =0, единичный вектор длин=1
Векторы a и b называются коллинеарными ( a
II b ), если они лежат на одной прямой или на параллельных прямых. Если коллинеарные векторы направлены в одну сторону, то они называются сонаправленными (a↑↑b).
Если коллинеарные векторы направлены в разные стороны, то они называются противоположно направленными ( a ↑↓b).
Векторы a и b называются равными ( a =b ), если они коллинеарны, одинаково направлены и их длины равны.
Три вектора a, b и c называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Сложение векторов (треугольное и параллелограммное сложение)
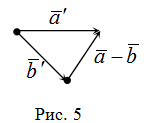
Разностью 
двух векторов 
и 
называется сумма вектора и вектора 
, который является противоположным вектору : 
3. Умножение вектора на число
10) Базис на плоскости и в пространствеОпределение: Базисом на плоскости и пространстве называется максимальная линейно независимая на плоскости или в пространстве система векторов (добавление к системе еще одного вектора делает ее линейно зависимой).
Таким образом, базисом на плоскости являются любые два неколлинеарных вектора, взятых в определенном порядке, а базисом в пространстве - любые три некомпланарных вектора, взятых в определенном порядке.
Пусть - базис в пространстве, тогда по Т.3 любой вектор пространства разлагаются единственным образом по базисным векторам
Коэффициенты разложения называются координатами вектора в базисе
: ={α
1,
α2, α
3}.
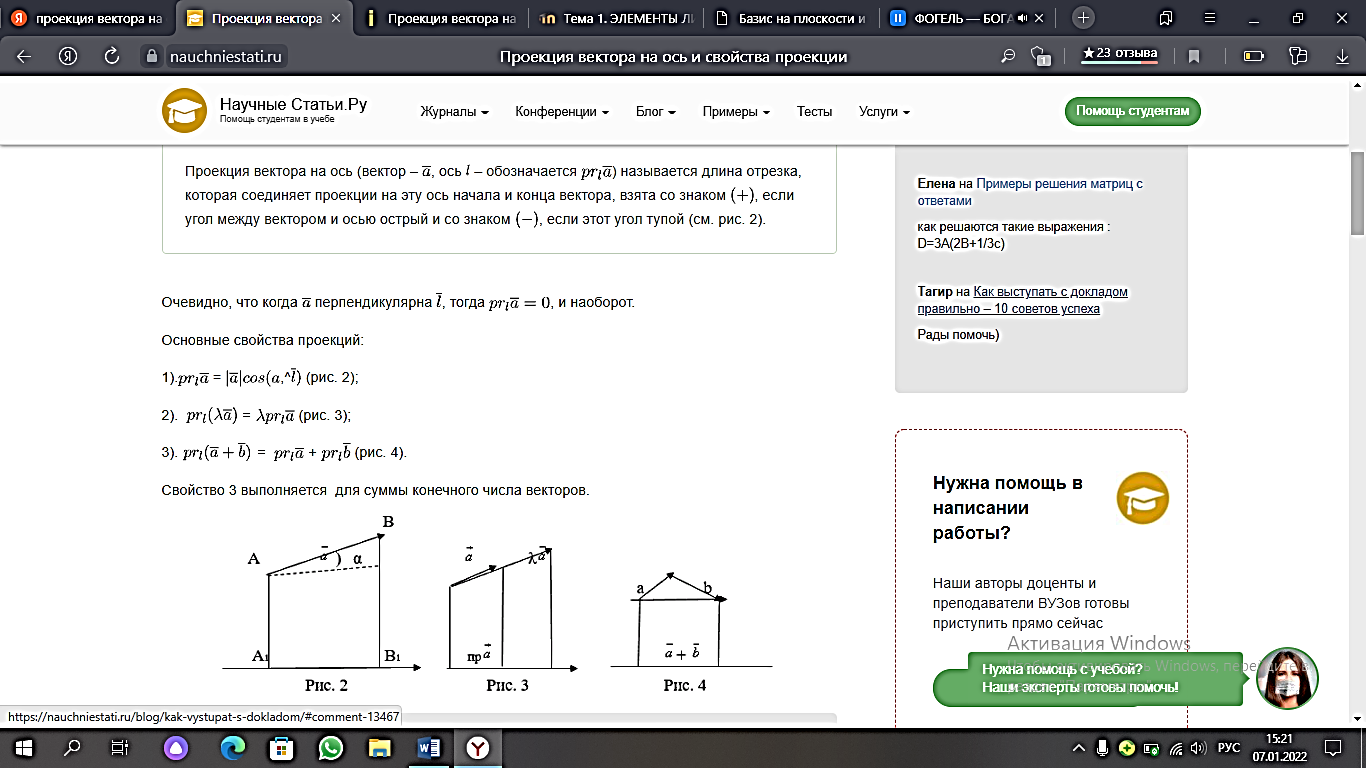11) 12)-
13-15)
Скачать 1.17 Mb.
называется определитель, составленный из элементов, оставшихся после вычеркивания 
стоки и 
столбца, на пересечении которых находится этот элемент. Минор элемента 
порядка имеет порядок 
. Будем его обозначать через 
.
, тогда 
.
, т.е 
, где 
–номер строки и 
-столбца, на пересечении которых находится данный элемент.
, тогда
=k(x-
),
(m1;n1;p1) и 
(m2;n2;p2). По определению скалярного произведения:
