Информатика. 1. Основные понятия и задачи информатики Вопрос Понятие, структура и задачи информатики
 Скачать 6.05 Mb. Скачать 6.05 Mb.
|
|
Тема 2. Математические основы информатики Вопрос 1. Системы счисления. Система счисления — это способ представления чисел с помощью символов (цифр), имеющих определенные количественные значения. В зависимости от способа изображения чисел выделяется два типа систем счисления: 1. Позиционные системы счисления, в которых количественное значение каждой цифры зависит от ее места (позиции) в числе, например, арабская система счисления. 2. Непозиционные системы счисления, в которых цифры не меняют своего количественного значения при смене позиции в числе, например, римская система счисления. В Римской системе счисления значение цифры не зависит от ее положения в записи числа. Например, число ХХХ. Здесь цифра Х в любом месте означает число десять (а вся запись – число 10+10+10=30). Непозиционные системы счисления неудобны для вычислений, поэтому в вычислительной технике используются только позиционные системы счисления. Основание позиционной системы счисления (P) — это количество различных цифр, используемых для изображения чисел в системе счисления. При этом сами значения цифр лежат в пределах от 0 до P – 1. В повседневной жизни мы имеем дело с десятичной системой счисления, где Р = 10 и используются арабские цифры от 0 до 9. А в то же время в электронных вычислительных машинах (или компьютерах) для записи данных и информации используется двоичная система счисления. Понятно, что в этом случае Р = 2 и используются только 2 символа: 0 и 1. Оба этих символа носят название двоичных единиц. В позиционной системе счисления любое число представляется суммой произведений коэффициентов на основание системы счисления Р в степени, соответствующей местоположению цифры в числе. Здесь коэффициенты и есть те цифры, из которых состоит число. Для простоты понимания вопроса ограничимся пока представлением лишь целых чисел. При этом первой справа цифре числа соответствует позиция «0», второй – «1» и т.д. В общем случае любое число A, состоящее из m знаков в целой части, в позиционной системе счисления с основанием P будет записано в следующем виде: A = am–1P m–1 + … + a1P1 + a0P 0, где нижние индексы 0…m – 1 определяют позицию (местоположение) цифры в записи числа. Например, десятичное число 469 можно представить в виде суммы: 469 = 4 · 102 + 6 · 101 + 9 · 100 Слева от знака равенства число записано в сокращенной записи, а справа – в виде суммы степеней десятки с соответствующими коэффициентами (полная запись числа). Как видим, последовательность цифр в краткой записи числа (слева от знака «=») состоит из коэффициентов при степенях основания системы счисления: 4, 6. 9. Чтобы представить то же число в двоичной системе счисления, сначала запишем его в виде суммы чисел, каждое из которых равно некоторой степени двойки: 469 = 256 + 128 + 64 + 16 + 4 +1 Как известно, 256 = 28, 128 = 27, 64 = 26, 32 = 25, 16 = 24, 8 = 23, 4 = 22, 2 = 21, 1 = 20. Значит, 469 = 1 · 28 + 1 · 27 + 1 · 26 + 0 · 25 + 1 · 24 + 0 · 23 + 1 · 22 + 0 · 21 + 1 · 20. Если теперь выпишем последовательность коэффициентов перед степенями двойки, получим двоичный код десятичного числа 469: 1 1 1 0 1 0 1 0 1 Приведём примеры записи десятичных чисел в двоичной системе.
Рассматривая двоичный код десятичных чисел, можно заметить, что у чётных чисел двоичный код оканчивается на 0, а у нечётных – на 1. Кроме рассмотренных систем счисления в информатике иногда используются и другие: восьмеричная(используются цифры 0, 1, ..., 7); шестнадцатеричная(для первых целых чисел от нуля до девяти используются цифры 0, 1, ..., 9, а для следующих чисел – от десяти до пятнадцати – в качестве цифр используются символы A, B, C, D, E, F). Приведём примеры записи чисел в этих системах. Восьмеричное число: 357(8) = 3 · 82 + 5 · 81 + 7 · 80 = 192 + 40 + 7 = 239 (10). Шестнадцатеричное число++ 3BE(16) = 3 · 162 + 11 · 161 + 14 · 160 = 768 + 176 + 14 = 958(10). Анализируя изложенный материал, можно сделать вывод: чтобы перевести число из одной системы счисления в другую, его следует представить в виде суммы произведений некоторых коэффициентов (выраженных в символах новой системы) на степени основания этой системы, а затем выписать значения этих коэффициентов в виде последовательности. Это и будет код числа в новой системе. Вопрос 2. Количественные характеристики информации. Кроме качественных характеристик информации, рассмотренных выше, информация обладает и количественными характеристиками. Их изучает специальная наука – теория информации. Важнейшим результатом теории информации является вывод о том, что в определенных, весьма широких условиях, можно, пренебрегая качественными особенностями информации, выразить ее количество числом, а следовательно, сравнивать количество информации, содержащейся в различных группах данных. Количеством информации называют числовую характеристику информации, отражающую ту степень неопределенности, которая исчезает после получения информации. Рассмотрим пример. Находясь осенним утром дома, мы предположили, что могут быть осадки, а могут и не быть, а если будут, то в виде снега или в виде дождя, то есть «то ли будет, то ли нет, то ли дождик, то ли снег». Затем, выглянув в окно, увидели пасмурное небо и с большой вероятностью предположили, в ближайшие часы осадки будут. То есть, после получения информации, у нас снизилось количество вариантов выбора. Далее, взглянув на наружный термометр, мы увидели, что температура отрицательная, значит, осадки следует ожидать в виде снега. Таким образом, получив последние данные о температуре, мы получили полную информацию о предстоящей погоде и исключили все варианты выбора, кроме одного. Приведенный пример показывает, что понятия «информация», «неопределенность», «возможность выбора» тесно связаны. Получаемая информация уменьшает число возможных вариантов выбора (т.е. неопределенность), а полная информация не оставляет вариантов вообще. Условно все подходы к определению количества информации можно разделить на пять видов: 1) энтропийный; 2) алгоритмический; 3) комбинаторный; 4) семантический; 5) прагматический. Первые три вида дают количественное определение сложности описываемого объекта или явления. Четвертый – описывает содержательность и новизну передаваемого сообщения для получателя (пользователя) сообщения. Наконец, пятый вид обращает внимание на полезность полученного сообщения для пользователя. Измерение информации: содержательный подход. Для человекаинформация тесно связана с его знаниями. Рассмотрим вопрос с этой точки зрения. Получение новой информации приводит к расширению знаний. Если некоторое сообщение приводит к уменьшению неопределенности нашего знания, то можно говорить, что такое сообщение содержит информацию. Отсюда следует вывод, что сообщение информативно (т.е. содержит ненулевую информацию), если оно пополняет знания человека. Например, прогноз погоды на завтра — информативное сообщение, а сообщение о вчерашней погоде неинформативно, так как нам это уже известно. Нетрудно понять, что информативность одного и того же сообщения может быть разной для разных людей. Например: «2 x 2=4» информативно для первоклассника, изучающего таблицу умножения, и неинформативно для старшеклассника. Но для того чтобы сообщение было информативно, оно должно быть еще понятно. Быть понятным – значит быть логически связанным с предыдущими знаниями человека. Определение «значение определенного интеграла равно разности значений первообразной подынтегральной функции на верхнем и на нижнем пределах», скорее всего, не пополнит знания и старшеклассника, так как оно ему непонятно. Для того чтобы понять данное определение, нужно закончить изучение элементарной математики и знать начала высшей. Получение всяких знаний должно идти от простого к сложному. И тогда каждое новое сообщение будет в то же время понятным, а значит, будет нести информацию для человека. Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными. Очевидно, что различать лишь две ситуации: «нет информации» — «есть информация» для измерения информации недостаточно. Нужна единица измерения, тогда мы сможем определять, в каком сообщении информации больше, а в каком – меньше. Единица измерения информации была определена в науке, которая называется теорией информации. Эта единица носит название «бит». Ее определение звучит так: «Сообщение, уменьшающее неопределенность знаний в два раза, несет 1 бит информации». Неопределенность знаний о некотором событии — это количество возможных результатов события. Рассмотрим классический пример – подбрасывание монеты. До эксперимента мы имеем неопределённость: либо выпадет «орел», либо «решка». То есть неопределённость – два возможных исхода. После подбрасывания монеты, неопределённость уменьшается вдвое и вообще исчезает – монета упала конкретной стороной. То есть, сообщение о том, что выпал, например, «орел» несёт информацию, количество которой равно 1 биту. Другой пример. После выполнения контрольной работы у студента имеется неопределенность, он не знает, какую оценку получил: «2», «3», «4» или «5». То есть количество возможных исходов равно 4. После объявления преподавателем результатов, он получает одно из четырех информационных сообщений: «2», «3», «4» или «5». Информационное сообщение об оценке за контрольную работу приводит к уменьшению неопределенности знания в четыре раза, так как получено одно из четырех возможных сообщений. То есть количество информации в сообщении равно 2 битам. Если обозначить возможное количество событий, или, другими словами, неопределенность знаний N, а буквой I количество информации в сообщении о том, что произошло одно из N событий, то можно записать формулу: 2I = N Итак, количество информации, содержащееся в сообщении о том, что произошло одно из N равновероятных событий, определяется из решения показательного уравнения: 2I = N. Таким образом, при двух равновероятных исходах эксперимента N = 2, I = 1 (бит), а при N = 4, I = 2 (бита). Измерение информации: алфавитный подход. Алфавитный подход – это способ измерения информации, который не связывает количество информации с содержанием сообщения. При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы. Применение алфавитного подхода удобно прежде всего при использовании технических средств работы с информацией. В этом случае теряют смысл такие понятия, как «новые — старые», «понятные — непонятные» сведения. Алфавитный подход является объективным способом измерения информации в отличие от субъективного содержательного подхода. Все множество используемых в языке символов будем традиционно называть алфавитом. Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, т.е. пропуск между словами. Полное количество символов алфавита принято называть мощностью алфавита. Будем обозначать эту величину буквой N. Например, мощность алфавита из заглавных русских букв, цифр и дополнительных символов (( ) . , ! ? « « : - ; (пробел)) – равна 54. Рассмотрим вопрос: сколько информации несет один символ в русском языке? Для простоты предположим, что каждый символ в тексте с одинаковой вероятностью может быть любым символом алфавита. Тогда, согласно известной нам формуле 2I =N, каждый такой символ несет I бит информации, которое можно определить из решения уравнения: 2I = 54. Получаем: I = 5.755 бит. Вот сколько информации несет один символ в русском тексте. А теперь для того, чтобы найти количество информации во всем тексте, нужно посчитать число символов в нем и умножить на I. Посчитаем, например, количество информации на одной странице книги. Пусть страница содержит 50 строк. В каждой строке – 60 символов. Значит, на странице умещается 50 x 60=3000 знаков. Тогда объем информации будет равен: 5,755бит х 3000 = 17265 бит. Сформулируем полученный вывод. При алфавитном подходе к измерению информации количество информации зависит не от содержания, а от размера текста и мощности алфавита. А что если алфавит состоит только из двух символов 0 и 1? В этом случае: N = 2; 2I = N = 2; I = 1. Значит, при использовании двоичной системы (алфавит состоит из двух знаков: 0 и 1) каждый двоичный знак несет 1 бит информации. Интересно отметить, что сама единица измерения информации «бит» получила свое название от английского сочетания «binary digit» – «двоичная цифра». Удобнее всего измерять информацию, когда размер алфавита N равен целой степени двойки. Например, если N = 16, то каждый символ несет 4 бита информации, потому что 24 = 16. А если N = 32, то один символ «весит» 5 бит. Ограничения на максимальный размер алфавита теоретически не существует. Однако есть алфавит, который можно назвать достаточным. Это алфавит мощностью 256 символов. В алфавит такого размера можно поместить все практически необходимые символы: латинские и русские буквы, цифры, знаки арифметических операций, всевозможные скобки, знаки препинания. Поскольку 256 = 28, то один символ этого алфавита «весит» 8 бит. Причем 8 бит информации – это настолько характерная величина, что ей даже присвоили свое название – байт. 1 байт = 8 бит Сегодня очень многие люди для подготовки писем, документов, статей, книг и пр. используют компьютерные текстовые редакторы. Компьютерные редакторы, в основном, работают с алфавитом размером 256 символов. В этом случае легко подсчитать объем информации в тексте. Если 1 символ алфавита несет 1 байт информации, то надо просто сосчитать количество символов; полученное число даст информационный объем текста в байтах. Пример. Пусть текст небольшой книжки, набранный с помощью компьютера, содержит 150 страниц, на каждой странице – 40 строк, в каждой строке — 60 символов. Значит, страница содержит 40 x 60 = 2400 байт информации. Объем всей информации в книге: 2400 х 150 = 360 000 байт. Вопрос 3. Представление информации в ЭВМ. Компьютер может обрабатывать числовую, текстовую, графическую, звуковую и видеоинформацию. Вся информация в ЭВМ представлена в виде двоичных кодов. Как известно (из предыдущего раздела), 1 бит – это наименьшая единица информации для обозначения одного двоичного разряда, способного принимать значение 0 или 1. Биты нумеруются справа налево, начиная с нулевого разряда. С помощью набора битов можно представить любой символ (число, букву или знак). Однако отражать данные в такой форме не совсем удобно, и биты группируются в пакеты по 8 бит. Поэтому обычно информация представляется байтами. Комбинируя возможные комбинации из 8 бит (байт), можно получить 256 (28) различных кодов. Для кодирования символов в ЭВМ используют кодовые таблицы. На сегодняшний день стандартом де-факто является таблица ASCII (American Standard Code for Information Interchange — американский стандартный код для обмена информацией), в котором каждый символ закодирован десятичным числом (от 0 до 255): коды 0…31 — для специальных (управляющих) клавиш; коды 32…127 — для цифр, латинских букв и стандартных знаков; коды 128…255 — для букв национальных алфавитов и специальных знаков. Кодировка согласно таблице ASCII (код принят в 1963 г.) используется в операционных системах семейства Windows, и ее часто называют кодировкой CP-1251 (Code Page — кодовая страница). Также существуют кодировки CP-866 (для DOS) и КОИ-81 (для Unix). В настоящее время широко распространилась альтернативная кодовая таблица (в стандарте Unicode), позволяющая представить большее количество символов. В ней на каждый символ отводится 2 байта, поэтому можно закодировать 65 536 (216) различных символов. Графическая информация (в отличие от текстовой) представляется на экране в виде растрового изображения, которое формируется из определенного количества строк, содержащих определенное количество точек (пикселей), имеющих свой цвет, заданный специальным кодом. В процессе кодирования изображения производится его пространственная дискретизация — построение изображения из большого количества отдельных цветных точек. Иначе кодируется звуковая информация. Любая звуковая волна имеет непрерывно меняющиеся частоту и амплитуду. При увеличении амплитуды сигнала усиливается громкость звука, а при увеличении его частоты повышается тональность. Для обработки в ЭВМ звуковая (аналоговая) информация кодируется в виде последовательности цифровых импульсов в процессе дискретизации звука. Дискретизация — это преобразование непрерывных звуков (или изображений) в набор дискретных значений в закодированной форме. Для представления числовой информации используется двоичная система счисления. В ЭВМ применяются две формы представления чисел: 1) в естественной форме (с фиксированной запятой) все числа изображаются в виде последовательности цифр с постоянным положением запятой, отделяющей целую часть от дробной, например, 12 345,6789. Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел и поэтому не всегда применима при вычислениях; 2) в вещественной форме (с плавающей запятой) каждое число изображается в виде двух групп цифр: мантиссы (абсолютная величина которой должна быть меньше 1) и порядка (целое число). Например, числу 2 000 000 в естественной форме соответствует число 0,2Е7 в вещественной форме, где 0,2 — мантисса числа, а 7 — порядок числа (степень, в которую надо возвести основание системы счисления (в нашем примере – 10) для получения исходного числа – 0,2 · 107 = 2 000 000). Эта форма представления имеет огромный диапазон отображения чисел и является основой в современных ЭВМ. В персональном компьютере могут обрабатываться поля постоянной и переменной длины. Размеры полей постоянной длины: полуслово — 1 байт; слово — 2 байта; двойное слово — 4 байта; расширенное слово — 8 байт. Числа с фиксированной запятой чаще всего имеют формат полуслова или слова, числа с плавающей запятой — формат двойного или расширенного слова. Поля переменной длины могут иметь любой целый размер от 1 до 256 байт. Для измерения «емкости» памяти используются биты и байты. В современных ЭВМ используются производные единицы измерения информации: 1 килобайт (КБайт — КБ) = 210 байт = 1024 байта; 1 мегабайт (МБайт — МБ) = 220 байт = 1024 KБ = 1 048 576 байт; 1 гигабайт (ГБайт — ГБ) = 230 байт = 1024 МБ; 1 терабайт (ТБайт — ТБ) = 240 байт = 1024 ГБ; 1 петабайт (ПБайт — ПБ) = 250 байт = 1024 ТБ; 1 экзабайт (ЭБайт — ЭБ) = 260 байт = 1024 ПБ; 1 зеттабайт (ЗБайт — ЗБ) = 270 байт = 1024 ЭБ; 1 йоттабайт (ЙБайт — ЙБ) = 280 байт = 1024 ЗБ. В физике термин «кило» означает 1000, а в информатике — 1024, так как это число более естественно для вычислительных машин, которые в основе своей арифметики используют число 2 (как человек применяет 10). Поэтому числа 10, 100, 1000 и т.д. удобны для человека, а числа 2, 4, 8, 16, …, 1024 (210) и т.д. «удобны» для ЭВМ. Например, одна страница стандартного машинописного текста формата А4 содержит примерно 3 KБ информации, а цветная фотография размером 10 см х 15 см – около 8 МБ (в несжатом виде). Вопрос 4. Элементы алгебры логики. В цифровой технике для передачи информации используются сигналы (кодовые слова), которые поступают на вход каждого узла ЭВМ, а на выходе при этом образуются новые сигналы (кодовые слова), представляющие собой результат обработки входных слов. Поэтому можно говорить, что выходное слово есть функция, для которой входной сигнал является аргументом. Такие функции называются функциями алгебры логики. Как и в классической математике, для задания функций алгебры логики обычно используется два способа: 1) аналитический, когда функция записывается формулой; этот способ позволяет определять значения функций для отдельных комбинаций аргументов; 2) табличный, когда строится таблица истинности, содержащая всевозможные сочетания значений аргументов и соответствующие им значения функций. Поскольку цифровые вычислительные машины оперируют только информацией, представленной в виде набора двоичных цифр «0» и «1», то действия, выполняемые над ней, отличаются от общепринятых. Основы алгебры логики, разработанные в XIX веке английским математиком Джорджем Булем, базируются на использовании только двух переменных: a и b. Алгебра логики (Булева алгебра) основана на трех операциях: 1. Конъюнкция (логическое умножение) — операция «И», определяемая четырьмя правилами: 0 и 0 = 0; 0 и 1 = 0; 1 и 0 = 0; 1 и 1 = 1. 3. Дизъюнкция (логическое сложение) — операция «ИЛИ», определяемая четырьмя правилами: 0 или 0 = 0; 0 или 1 = 1; 1 или 0 = 1; 1 или 1 = 1. 4. Инверсия (логическое отрицание) — операция «НЕ», когда значение переменной изменяется на обратное (противоположное), то есть определяемая двумя правилами: не 0 = 1; не 1 = 0. Логические преобразования осуществляются в компьютере с помощью специальных логических устройств (элементов). Так как существует три основных логических операции, то выделяют три базовых логических элемента: «И», «ИЛИ», «НЕ» (рис. 1).  Рис. 1. Обозначения базовых логических элементов Кроме того, существуют различные нестандартные элементы, представляющие собой комбинации базовых элементов, например, элемент Шеффера, элемент Пирса (рис. 2). 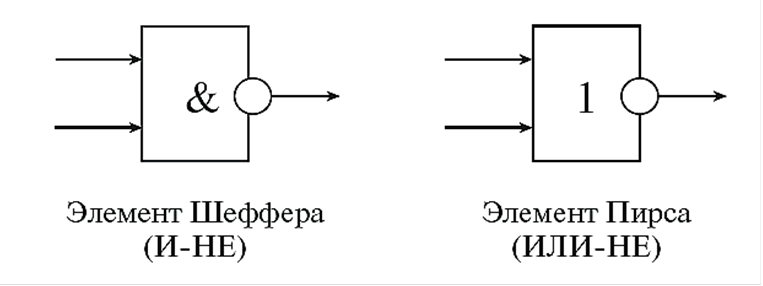 Рис. 2. Обозначения нестандартных логических элементов Принцип работы каждого логического элемента поясняется аналитически (формулой) или таблицей истинности, указывающей значение функции при заданных значениях переменных. В современных ЭВМ все логические элементы реализуются в виде специальных микросхем, которые выполняют определенные функции. Практические задания: 1. Расставьте термины напротив их определений. Термины: система счисления, алфавит системы счисления, мощность алфавита, основание системы счисления.
2. Заполните пустые клетки таблицы последовательными числами в системах счисления с основанием 2, 8, 16.
3. Переведите следующие числа из двоичной системы счисления в десятичную: а) 100101; б) 110011; в) 110011; г) 100010; д) 111000. 4. Какое количество информации содержит сообщение о выпадении грани с числом 3 на шестигранном игральном кубике? 5. Заполните таблицу вычисленными значениями логических операций при А = 1 и В = 0.
|
