1. озз. Определение, разделы дисциплины, задачи, структура. Роль дисциплины в системе мед образования, практической деятельности врачаспециалиста и организаций здравоохранения
 Скачать 2.59 Mb.
|
|
14. Вариационный ряд. Виды вариационных рядов. Величины, характеризующие вариационный ряд (мода, медиана, средняя арифметическая). Методика расчета. Оценка достоверности различий средних величин. Вариационный ряд — это статистический ряд, показывающий распределение изучаемого явления по величине какого-либо количественного признака. Например, больных по возрасту, по срокам лечения, новорожденных по весу и т.п. Варианта — отдельные значения признака, по которому проводится группировка (обозначается V). Частота— число, показывающее, как часто встречается та или иная варианта (обозначается P). Сумма всех частот показывает общее числонаблюдений и обозначается n. Разность между наибольшей и наименьшей вариантой вариационного ряда называется размахом или амплитудой. Различают вариационные ряды: 1. Прерывные (дискретные) и непрерывные. Ряд считается непрерывным, если группировочный признак может выражаться дробными величинами (вес, рост т.п.), прерывным, если группировочный признак выражается только целым числом (дни нетрудоспособности, число ударов пульса и т.п.). 2.Простые и взвешенные. Простой вариационный ряд представляет собой ряд, в котором количественное значение варьирующего признака встречается один раз. Во взвешенном вариационном ряду количественные значения варьирующего признака повторяются с определённой частотой. 3. Сгруппированные (интервальные) и несгруппированые. Сгруппированный ряд имеет варианты, объединённые в группы, объединяющие их по величине в пределах определённого интервала. В несгруппированном ряду каждой отдельной варианте соответствует определённая частота. 4. Четные и нечетные. В чётных вариационных рядах сумма частот или общее число наблюдений выражено чётным числом, в нечётных ― нечётным. 5. Симметричные и асимметричные. В симметричном вариационном ряду все виды средних величин совпадают или очень близки (мода, медиана, среднее арифметическое). В зависимости от характера изучаемых явлений, от конкретных задач и целей статистического исследования, а также от содержания исходного материала, в санитарной статистике применяются следующие виды средних величин: структурные средние (мода, медиана); средняя арифметическая; средняя гармоническая; средняя геометрическая; средняя прогрессивная. Мода (Мо) — величина варьирующего признака, которая более часто встречается в изучаемой совокупности т.е. варианта, соответствующая наибольшей частоте. Находят ее непосредственно по структуре вариационного ряда, не прибегая к каким-либо вычислениям. Она обычно является величиной очень близкой к средней арифметической и весьма удобна в практической деятельности. Медиана (Ме)— делящая вариационный ряд (ранжированный, т.е. значения вариант располагаются в порядке возрастания или убывания) на две равные половины. Медиана вычисляется при помощи так называемого нечетного ряда, который получают путем последовательного суммирования частот. Если сумма частот соответствует четному числу, тогда за медиану условно принимают среднюю арифметическую из двух средних значений. Мода и медиана применяются в случае незамкнутой совокупности, т.е. когда наибольшая или наименьшая варианты не имеют точной количественной характеристики (например, до 15 лет, 50 и старше и т.п.). В этом случае среднюю арифметическую (параметрические характеристики) рассчитать нельзя. Средняя арифметическая — самая распространенная величина. Средняя арифметическая обозначается чаще через М. Различают среднюю арифметическую простую и взвешенную. Средняя арифметическая простаявычисляется: ― в тех случаях, когда совокупность представлена простым перечнем знаний признака у каждой единицы; ― если число повторений каждой варианты нет возможности определить; ― если числа повторений каждой варианты близки между собой. Средняя арифметическая простая исчисляется по формуле:  ,где V — индивидуальные значения признака; n — число индивидуальных значений;  — знак суммирования.Таким образом, простая средняя представляет собой отношение суммы вариант к числу наблюдений. Пример: определить среднюю длительность пребывания на койке 10 больных пневмонией: 16 дней — 1 больной; 17–1; 18–1; 19–1; 20–1; 21–1; 22–1; 23–1; 26–1; 31–1.  койко-дня.Средняя арифметическая взвешеннаяисчисляется в тех случаях, когда индивидуальные значения признака повторяются. Ее можно вычислять двояким способом: 1. Непосредственным (среднеарифметическим или прямым способом) по формуле:  ,где P — частота (число случаев) наблюдений каждой варианты. Таким образом, средняя арифметическая взвешенная представляет собой отношение суммы произведений вариант на частоты к числу наблюдений. 2. С помощью вычисления отклонений от условной средней (по способу моментов). Основой для вычисления взвешенной средней арифметической является: ― сгруппированный материал по вариантам количественного признака; ― все варианты должны располагаться в порядке возрастания или убывания величины признака (ранжированный ряд). Для вычисления по способу моментов обязательным условием является одинаковый размер всех интервалов. По способу моментов средняя арифметическая вычисляется по формуле: 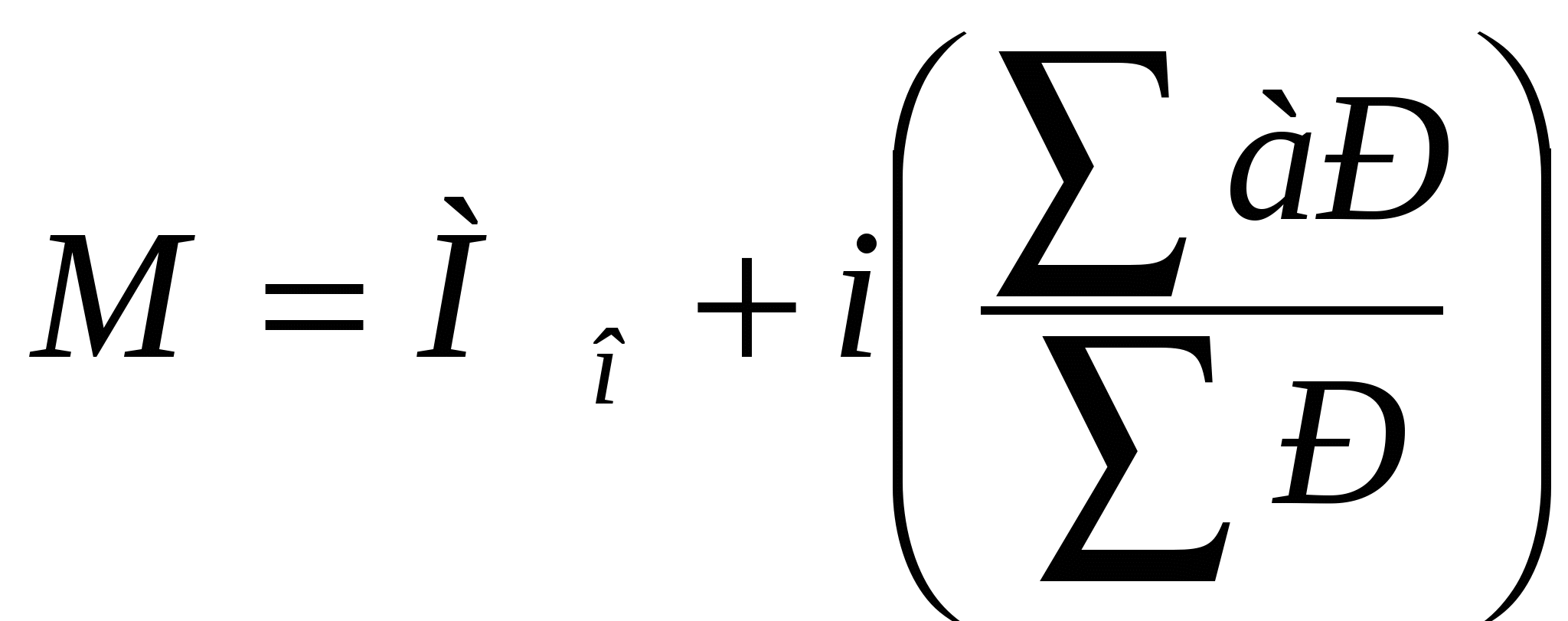 ,где Мо — условная средняя, за которую чаще принимают величину признака, соответствующую наибольшей частоте, т.е. которая чаще повторяется (Мода). i — величина интервала. a — условное отклонение от условий средней, представляющее собой последовательный ряд чисел (1, 2 и т.д.) со знаком + для вариант больших условной средней и со знаком–(–1, –2 и т.д.) для вариант, которые ниже условной средней. Условное же отклонение от варианты, принятой за условную среднюю равно 0. P — частоты.  — общее число наблюдений или n.Пример: определить средний рост мальчиков 8 лет непосредственным способом (таблица1). Т а б л и ц а 1
n = 100 12234 Центральная варианта ― середина интервала ― определяется как полу сумма начальных значений двух соседних групп:  ;  и т.д.Произведение VP получают путем умножения центральных вариант на частоты  ;  и т.д. Затем полученные произведения складывают и получают  , которую делят на число наблюдений (100) и получают среднюю арифметическую взвешенную. см.Эту же задачу решим по способу моментов, для чего составляется следующая таблица 2: Т а б л и ц а 2
n=100  В качестве Мо принимаем 122, т.к. из 100 наблюдений у 33 человек рост был 122см. Находим условные отклонения (a) от условной средней в соответствии с вышесказанным. Затем получаем произведение условных отклонений на частоты (aP) и суммируем полученные величины (  ). В итоге получится 17. Наконец, данные подставляем в формулу: При изучении варьирующего признака нельзя ограничиваться только вычислением средних величин. Необходимо вычислять и показатели, характеризующие степень разнообразия изучаемых признаков. Величина того или иного количественного признака неодинакова у всех единиц статистической совокупности. Характеристикой вариационного ряда является среднее квадратичное отклонение ( 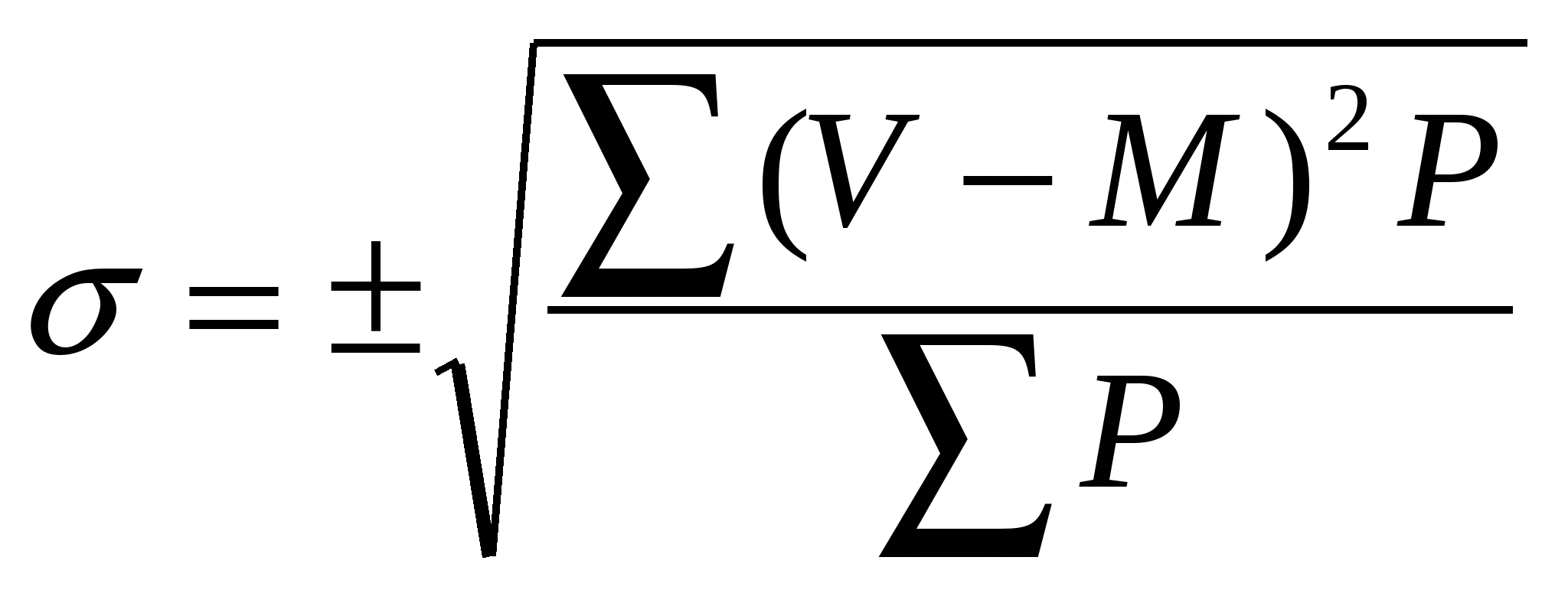 ), которое показывает разброс (рассеивание) изучаемых признаков относительно средней арифметической, т.е. характеризует колеблемость вариационного ряда. Оно может определяться непосредственным способом по формуле: Среднее квадратичное отклонение равняется квадратному корню из суммы произведений квадратов отклонений каждой варианты от средней арифметической (V–M)2 на свои частоты деленной на сумму частот (  ).Пример вычисления: определить среднее число больничных листов, выдаваемых в поликлинике за день (таблица 3). Т а б л и ц а 3
n=20 120 23  ;  В знаменателе при числе наблюдений менее 30 необходимо от отнимать единицу.Если ряд сгруппирован с равными интервалами, тогда можно определить среднее квадратичное отклонение по способу моментов: 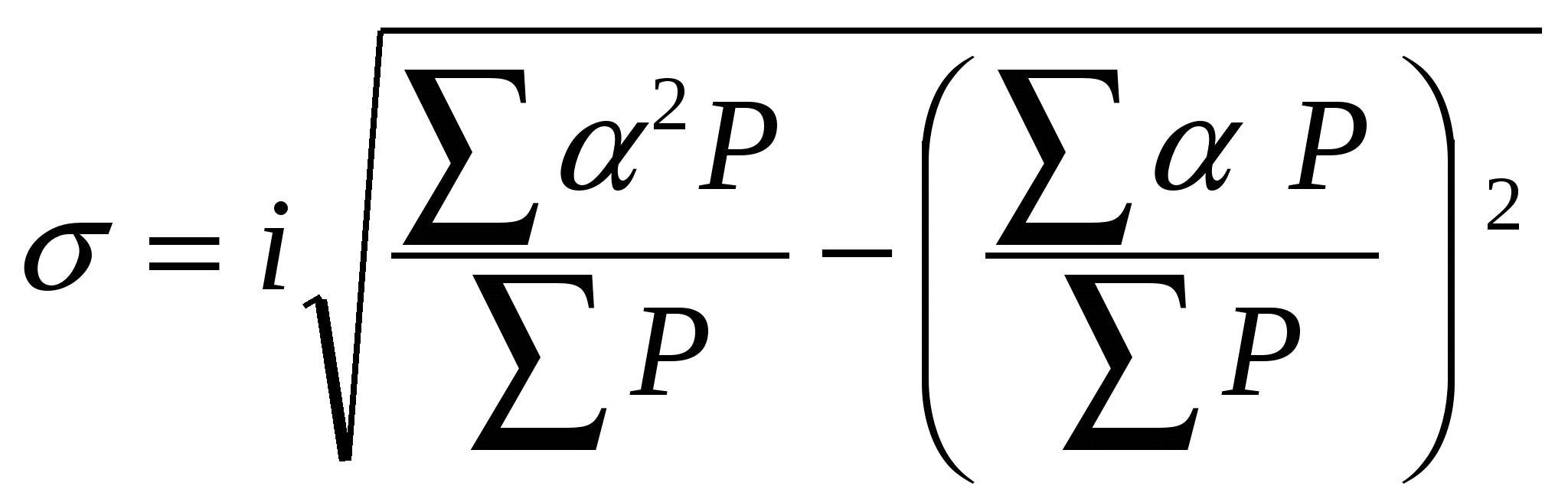 ,где i — величина интервала;  — условное отклонение от условной средней;P — частоты вариант соответствующих интервалов; — общее число наблюдений.Пример вычисления: Определить среднюю длительность пребывания больных на терапевтической койке (по способу моментов) (таблица 4): Т а б л и ц а 4
400 86 318  ; .Бельгийский статистик А. Кетле обнаружил, что вариации массовых явлений подчиняются закону распределения ошибок, открытому почти одновременно К. Гауссом и П. Лапласом. Кривая, отображающая это распределение, имеет вид колокола. По нормальному закону распределения колеблемость индивидуальных значений признака находится в пределах  , что охватывает 99,73% всех единиц совокупности.Подсчитано, что если к средней арифметической прибавить и отнять 2  , то в пределах полученных величин находится 95,45% всех членов вариационного ряда и, наконец, если к средней арифметической прибавить и отнять 1, то в пределах полученных величин будут находиться 68,27% всех членов данного вариационного ряда. В медицине с величиной  1 связано понятие нормы. Отклонение от средней арифметической больше, чем на 1, но меньше, чем на 2 является субнормальным, а отклонение больше, чем на 2 ненормальным (выше или ниже нормы).В санитарной статистике правило трех сигм применяется при изучении физического развития, оценке деятельности учреждений здравоохранения, оценке здоровья населения. Это же правило широко применяется в народном хозяйстве при определении стандартов. Таким образом, среднее квадратичное отклонение служит для: ― измерения дисперсии вариационного ряда; ― характеристики степени разнообразия признаков, которые определяются коэффициентом вариации:  Если коэффициент вариации более 20% — сильное разнообразие, от 20 до 10% — среднее, менее 10% — слабое разнообразие признаков. Коэффициент вариации в известной мере является критерием надежности средней арифметической. |
