1. озз. Определение, разделы дисциплины, задачи, структура. Роль дисциплины в системе мед образования, практической деятельности врачаспециалиста и организаций здравоохранения
 Скачать 2.59 Mb. Скачать 2.59 Mb.
|
|
Косвенный метод стандартизации показателей применяется в двух случаях: при отсутствии данных о составе явления (больных, умерших и т.д.), т.е. числителя интенсивного показателя; при наличии малых чисел изучаемого явления. Суть метода заключается в том, что за стандарт принимают специальные интенсивные коэффициенты (например, летальность больных в каком-либо отделении многопрофильной больницы) и рассчитывают так называемые ожидаемые числа заболеваний для сравниваемых групп больных с учетом их фактической численности. Вычисление стандартизованных коэффициентов косвенным способом можно разбить на три этапа: I этап ― выбор стандарта. Для стандарта чаще используются данные извне (опубликованные в литературе, отчетные данные) при условии, что эти коэффициенты близки по уровням к предполагаемой летальности, заболеваемости, смертности, инвалидности изучаемого населения. Реже используются собственные данные в сумме по сравниваемым группам или по одной группе с наибольшим количеством наблюдений; II этап ― вычисление «ожидаемых» чисел на основе стандарта и фактического состава сравниваемых групп населения; III этап ― вычисление стандартизованных коэффициентов по формуле: Стандартизованный коэффициент = Общий показатель стандарта х х Фактическое число изучаемого явления. Ожидаемое число изучаемого явления Косвенный метод стандартизации имеет очень большое значение для анализа деятельности лечебно-профилактических учреждений. При наличии стандарта летальности, частоты осложнений по каждой нозологической форме можно рассчитать «ожидаемые» числа и показатели с учетом разнообразного состава больных в отделениях. Обратный метод стандартизации в деятельности врача появился относительно недавно [Керридж, 1958]. Этот метод используется реже, чем прямой и косвенный. Обратный метод стандартизации используется при отсутствии данных о составе среды, т.е. знаменателя для расчета интенсивных показателей. Результаты этого метода тем точнее, чем более дробные возрастные интервалы применяются при стандартизации. Расчет стандартизованных показателей обратным методом проводится в 3 этапа: I этап ― выбор стандарта (повозрастные коэффициенты заболеваемости или смертности населения). За стандарт чаще принимаются внешние данные: уровни заболеваемости или смертности за предыдущие годы либо коэффициенты заболеваемости или смертности по другим районам, но не по собственным, а по иным источникам. За стандарт принимаются и собственные данные, если можно рассчитать специальные коэффициенты; II этап ― расчет ожидаемой численности населения в каждой изучаемой группе в соответствии с принятыми за стандарт показателями заболеваемости (смертности) населения и фактическим числом заболевших (умерших) в отдельных возрастных группах населения; III этап ― вычисление стандартизованных показателей поформуле: Стандартизованный коэффициент = Ожидаемая численность населения х Фактическая численность населения х Общий интенсивный коэффициент стандарта. У обратного метода много общего с косвенным, только «ожидаемые» числа рассчитываются не для изучаемых явлений, а для численности населения. Таким образом, применение любого из трех методов стандартизации в оценке здоровья населения дает врачу возможность показать зависимость различных показателей здоровья населения от тех или иных факторов риска, объективно оценить проводимую профилактическую работу, выявить наиболее значимые приоритетные факторы, определяющие уровень заболеваемости, смертности, инвалидности, рождаемости и другие показатели здоровья в определенной больнице, поликлинике, на конкретном предприятии, в районе, области и т.д. В заключение необходимо еще раз подчеркнуть, что выбор конкретного метода стандартизации зависит от того, насколько полный статистический материал имеется в наличии. Пря мой метод дает более надежные результаты, но в случае невозможности его применения следует использовать косвенный или обратный методы стандартизации: они достаточно точны для практического применения. Стандартизация позволяет нам сделать правильный вывод о том, действительно ли имеется разница общих интенсивных коэффициентов в сравниваемых коллективах или эти различия зависят только от не одинаковой структуры коллективов. Важно помнить, что величина стандартизованных коэффициентов зависит от выбора стандарта, поэтому сравнение стандартизованных показателей (разных больных, поликлиник, районов, областей, стран и т.д.) можно проводить, если они вычислены с применением одного и того же стандарта. С учетом этого большое значение имеет создание единых стандартов и формирование базы стандартов с целью их широкого использования при анализе различных показателей здоровья. Кроме того, стандартизованные коэффициенты, как величины условные, пригодны прежде всего для сравнения между собой с целью элиминирования (исключения) различных факторов, определяющих уровень здоровья населения. Для знания реальных размеров явления (смертность, летальность, заболеваемость населения т.д.) необходимо применять обычные интенсивные (общие и специальные) коэффициенты. Метод корреляции Все явления в природе и обществе находятся во взаимной связи. Выяснение наличия связей между изучаемыми явлениями ― одна из важных задач статистики. Многие медико-биологические и медико-социальные исследования требуют установления вида связи (зависимости) между случайными величинами. Сама постановка большого круга задач в медицинских исследовательских работах предполагает построение и реализацию алгоритмов «фактор ― отклик», «доза ― эффект». Зачастую нужно установить наличие эффекта при имеющейся дозе и оценить количественно полученный эффект в зависимости от дозы. Решение этой задачи напрямую связано с вопросом прогнозирования определенного эффекта и дальнейшего изучения механизма возникновения именно такого отклика. Как известно, случайные величины X и Y могут быть либо независимыми, либо зависимыми. Зависимость случайных величин подразделяется на функциональную и статистическую (корреляционную). Функциональная зависимость ― такой вид зависимости, когда каждому значению одного признака соответствует точное значение другого. В математике функциональную зависимость переменной X от переменной Y называют зависимостью вида X= f(Y), где каждому допустимому значению Y ставится в соответствие по определенному правилу единственно возможное значение X. Например: взаимосвязь площади круга (S) и длины окружности (L). Известно, что площадь круга и длина окружности связаны вполне определенным отношением S = rL, где r – радиус круга. Умножив длину окружности на половину ее радиуса, можно точно определить площадь крута. Такую зависимость можно считать полной (исчерпывающей). Она полностью объясняет изменение одного признака изменением другого. Этот вид связи характерен для объектов, являющихся сферой приложения точных наук. В медико-биологических исследованиях сталкиваться с функциональной связью приходится крайне редко, поскольку объекты этих исследований имеют большую индивидуальную вариабельность (изменчивость). С другой стороны, характеристики биологических объектов зависят, как правило, от комплекса большого числа сложных взаимосвязей и не могут быть сведены к отношению двух или трех факторов. Во многих медицинских исследованиях требуется выявить зависимость какой-либо величины, характеризующей результативный признак, от нескольких факториальных признаков. Дело в том, что на формирование значений случайных величин X и Y оказывают влияние различные факторы. Обе величины ― и X, и Y ― являются случайными, но так как имеются общие факторы, оказывающие влияние на них, то X и Y обязательно будут взаимосвязаны. И связь эта уже не будет функциональной, поскольку в медицине и биологии часто бывают факторы, влияющие лишь на одну из случайных величин и разрушающие прямую (функциональную) зависимость между значениями X и Y. Связь носит вероятностный, случайный характер, в численном выражении меняясь от испытания к испытанию, но эта связь определенно присутствует и называется корреляционной. Корреляционной является зависимость массы тела от роста, поскольку на нее влияют и многие другие факторы (питание, здоровье, наследственность и т.д.). Каждому значению роста (X) соответствует множество значений массы (Y), причем, несмотря на общую тенденцию, справедливую для средних: большему значению роста соответствует и большее значение массы, ― в отдельных наблюдениях субъект с большим ростом может иметь и меньшую массу. Корреляционной будет зависимость заболеваемости от воздействия внешних факторов, например запыленности, уровня радиации, солнечной активности и т.д. Имеется корреляционная зависимость между дозой ионизирующего излучения и числом мутаций, между пигментом волос человека и цветом глаз, между показателями уровня жизни населения и смертностью, между числом пропущенных студентами лекций и оценкой на экзамене. Именно корреляционная зависимость наиболее часто встречается в природе в силу взаимовлияния и тесного переплетения огромного множества самых разных факторов, определяющих значение изучаемых показателей. Корреляционная зависимость ― это зависимость, когда при изменении одной величины изменяется среднее значение другой. Строго говоря, термин «зависимость» при статистической обработке материалов медико-биологических исследований должен использоваться весьма осторожно. Это связано с природой статистического анализа, который сам по себе не может вскрыть истинных причинно-следственных отношений между факторами, нередко опосредованными третьими факторами, причем эти третьи факторы могут лежать вообще вне поля зрения исследователя. С помощью статистических критериев можно дать только формальную оценку взаимосвязей. Попытки механически перенести данные статистических расчетов в объективную реальность могут привести к ошибочным выводам. Например, утверждение: «Чем громче утром кричат воробьи, тем выше встает солнце», несмотря на явную несуразность, с точки зрения формальной статистики вполне правомерно. Таким образом, термин «зависимость» в статистическом анализе подразумевает только оценку соответствующих статистических критериев. Корреляционные связи называют также статистическими (например, зависимость уровня заболеваемости от возраста населения). Эти связи непостоянны, они колеблются от нуля до единицы. Ноль означает отсутствие зависимости между признаками, а единица ― полную, или функциональную, связь, когда имеется зависимость только от одного признака. Мерой измерения статистической зависимости служат раз личные коэффициенты корреляции. Выбор метода для определения взаимосвязей обусловлен видом самих признаков и способами их группировки. Для количественных данных применяют линейную регрессию и коэффициент линейной корреляции Пирсона. Для качественных признаков применяются таблицы сопряженности и рассчитываемые на их основе коэффициенты сопряженности (С и Ф), Чупрова (К). Для при знаков, сформированных в порядковой (ранговой, балльной) шкале, можно применять ранговые коэффициенты корреляции Спирмена или Кендэла. Любую существующую зависимость по направлению связи можно подразделить на прямую и обратную. Прямая зависимость ― это зависимость, при которой увеличение или уменьшение значения одного признака ведет, соответственно, к увеличению или уменьшению второго. Например: при увеличении температуры возрастает давление газа (при его неизменном объеме), при уменьшении температуры снижается и давление. Обратная зависимость имеется тогда, когда при увеличении одного признака второй уменьшается, и наоборот: при уменьшении одного второй увеличивается. Обратная зависимость, или обратная связь, является основой нормального регулирования почти всех процессов жизнедеятельности любого организма. Оценка силы корреляционной связи проводится в соответствии со шкалой тесноты. Если размеры коэффициента корреляции от ±0,9(9) до ±0,7, то связь сильная, коэффициенты корреляции от ±0,31 до ±0,69 отражают связь средней силы, а коэффициенты от ±0,3 до нуля характеризуют слабую связь. Известное представление о наличии или отсутствии корреляционной связи между изучаемыми явлениями или признаками (например, между массой тела и ростом) можно получить графически, не прибегая к специальным расчетам. Для этого достаточно на чертеже в системе прямоугольных координат отложить, например, на оси абсцисс величины роста, а на оси ординат ― массы тела и нанести ряд точек, каждая из которых соответствует индивидуальной величине веса при данном росте обследуемого. Если полученные точки располагаются кучно по наклонной прямой к осям ординат в виде овала (эллипса) или по кривой линии, то это свидетельствует о зависимости между явлениями. Если же точки расположены беспорядочно или на прямой, параллельной абсциссе либо ординате, то это говорит об отсутствии зависимости. По форме корреляционные связи подразделяются на прямолинейные, когда наблюдается пропорциональное изменение одного признака в зависимости от изменения другого (графически эти связи изображаются в виде прямой линии или близкой к ней), и криволинейные, когда одна величина признака изменяется непропорционально изменению другой (на графике эти связи имеют вид параболы, эллипса или иной кривой линии). Таким образом, корреляционные связи различаются по характеру (прямые и обратные), по форме (прямолинейные и криволинейные), по силе (сильная, средняя, слабая). И, наконец, корреляционные связи могут иметь разную достоверность. Существуют статистически значимые связи с высокой вероятностью достоверного прогноза минимум на 95 %, максимум ― на 99 % и выше. И могут быть статистически незначимые корреляционные связи, когда вероятность достоверного прогноза ниже 95 %. В основу исчисления коэффициента корреляции берется оценка совпадений колебаний значений взаимосвязанных признаков. Если объективно существующие колебания (вариации) этих значений совпадают, то можно говорить о наличии корреляции. Если колебания не совпадают, корреляции нет. Коэффициент линейной корреляции Пирсона При наличии прямолинейной связи между взаимосвязанными количественными признаками, особенно при большом числе наблюдений, рациональнее прибегать к параметрическим методам оценки, которые требуют вычисления определенных параметров: средней величины (М), среднего квадратического отклонения, средней ошибки (т). При этом вычисление связи проводится по формуле 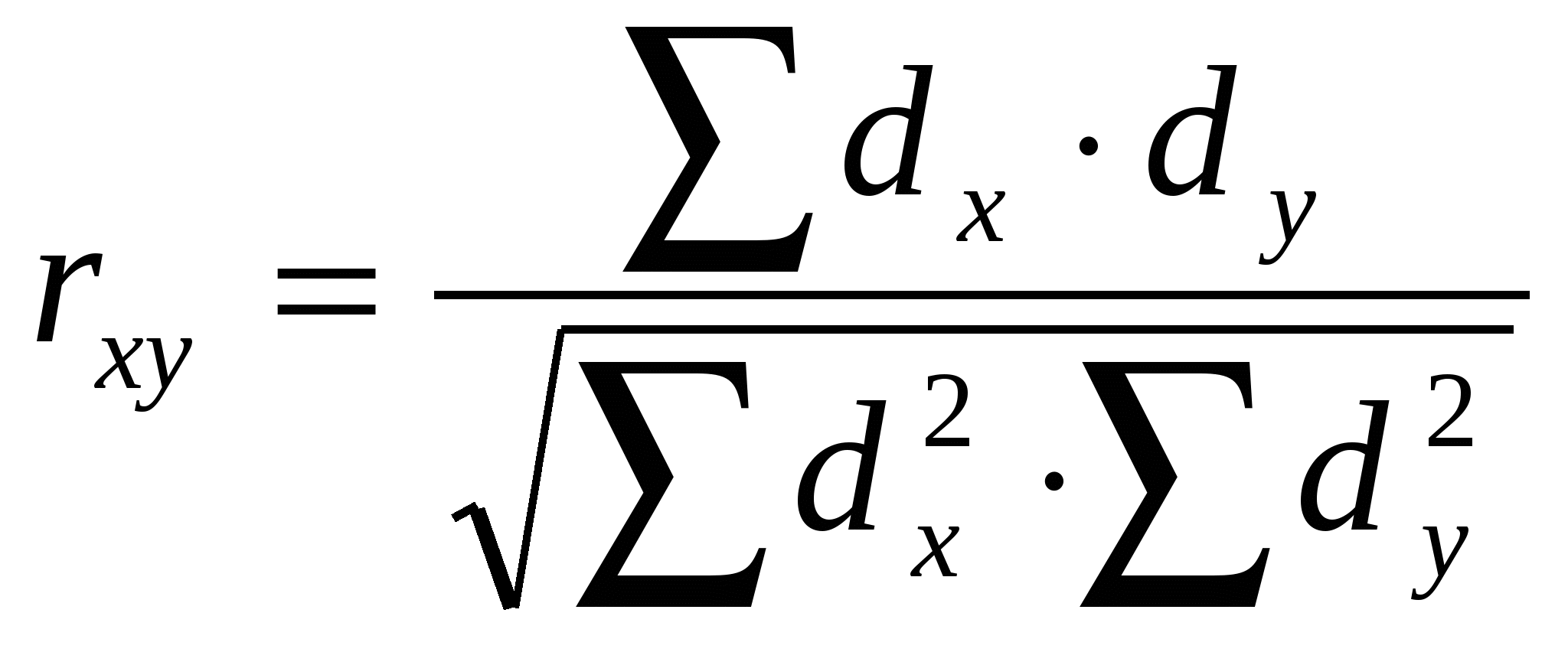 , ,где rху – коэффициент линейной корреляции между двумя признаками X и Y; d ― отклонение от средних арифметических данных ряда X и ряда Y. Алгоритм расчета коэффициента линейной корреляции состоит из трех основных этапов: I этап ― определение средних арифметических Мх Му для ряда X и ряда Y; II этап ― расчет отклонений чисел X и Y от средней арифметической этих рядов; III этап ― определение квадратов отклонений dх2и dy2 и произведения dхdy,, затем производится расчет сумм этих значений: dх2и dy2 и dxdy и вычисление по формуле Пирсона. Коэффициент линейной корреляции Пирсона наиболее быстро определяется по приведенной выше формуле на небольшом числе наблюдений, которые представлены в виде простых вариационных рядов, где частоты, как известно, равны единице. Это прямой путь вычисления коэффициента корреляции на основе использования средних величин и отклонений от них. Однако когда имеется большое число наблюдений и данные сгруппированы с определенным интервалом, т.е. представлены в виде взвешенных сгруппированных вариационных рядов, вычисление rху производится непрямым путем (способом) на основе метода Бравэ. Для вычисления к оэффициента корреляции при этих условиях необходимо строить корреляционную решетку (таблицу сопряженности). Такие условия на практике чаще всего встречаются при изучении и оценке физического развития отдельных групп населения. Результаты исследования в таблице сопряженности могут быть представлены как в разном, так и в одинаковом числе групп для подлежащего и сказуемого таблицы. Поскольку полученные коэффициенты корреляции определяются зачастую на материалах выборочной совокупности, всегда необходимо убеждаться в их надежности. Репрезентативность (представительность) коэффициента может определяться по специальным таблицам или через его ошибку где т – средняя ошибка коэффициента корреляции; rху ― коэффициент корреляции; n ― число коррелируемых пар. Достоверным выборочный коэффициент корреляции считают только тогда, когда его величина превышает свою среднюю ошибку в 3 раза и более. Оценку значимости проводят и по критерию (Стьюдента). Его величину определяют по формуле: 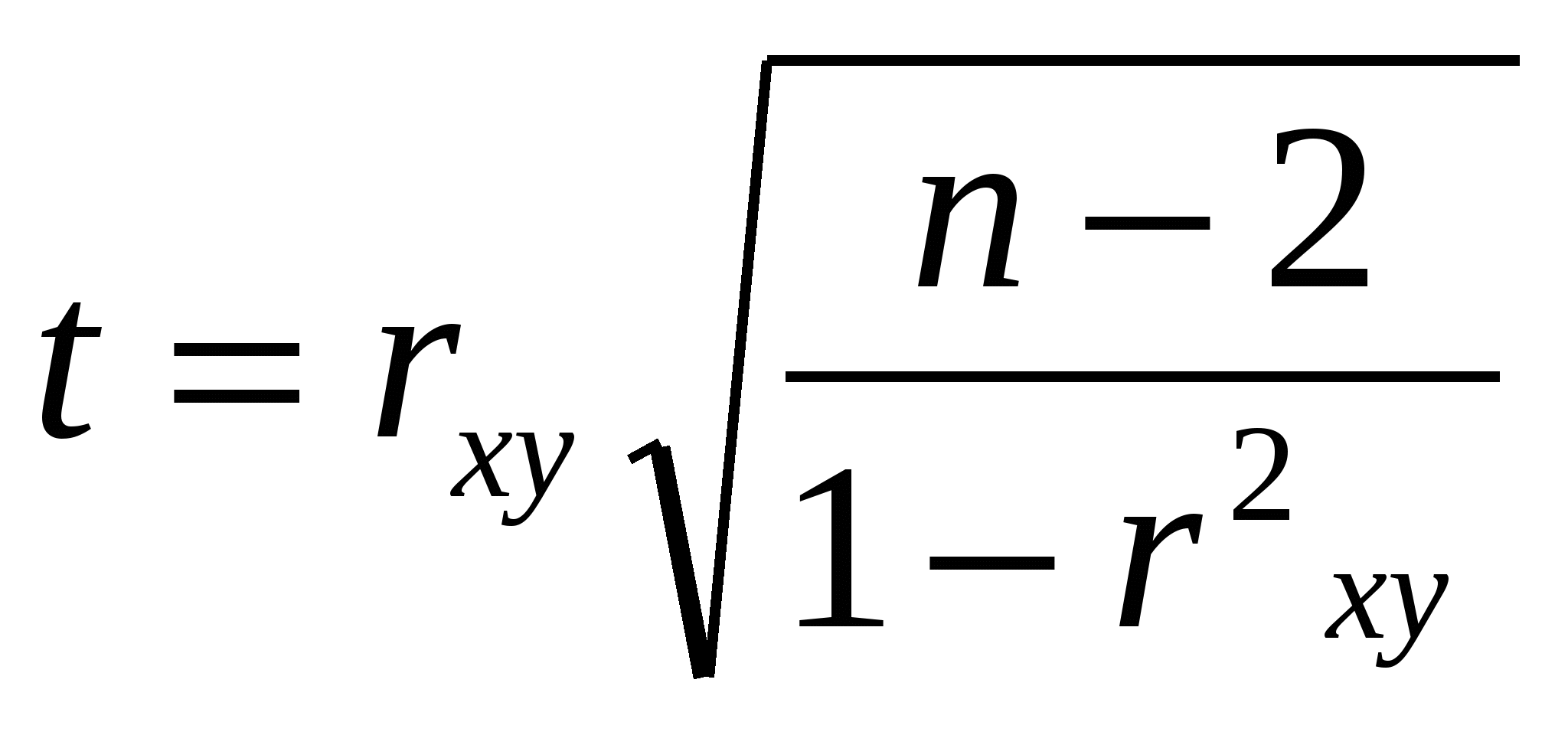 . . |
