1. озз. Определение, разделы дисциплины, задачи, структура. Роль дисциплины в системе мед образования, практической деятельности врачаспециалиста и организаций здравоохранения
 Скачать 2.59 Mb.
|
|
11. Экстенсивные коэффициенты и коэффициенты наглядности, методика расчета, область применения. Экстенсивный показатель (показатель распределения, состава явления, удельного веса) — показатель структуры явления. К таковым, например, относятся: показатель структуры причин смертности, показатель структуры причин младенческой смертности, показатель структуры заболеваемости, показатели распределения населения по полу, образованию, месту жительства, возрастной состав населения, удельный вес детей в структуре населения и т.д. Методика расчета: э.п. = (часть явления / целое явление)  основание.Основание — чаще всего 100, экстенсивный показатель выражается в %. Например: в 2006 году число всех заболеваний детей в детском саду составило 102 случая, в том числе 50 случаев энтеритов и 52 случая дизентерии. Если принять все случаи за 100 %, заболеваемость энтеритом составит — 50/102 100% = 49%, а заболеваемость дизентерией — 52/102 100% = 51%.Показатель наглядности — показатель, который используется для того, чтобы охарактеризовать изменения явления в динамике. Методика расчета: первоначально исходный или конечный (либо любой другой) уровень принимают за 1 или 100, а затем путем составления пропорций для каждого уровня находят, во сколько раз или на сколько процентов произошло уменьшение либо увеличение. 12. Общие положения о параметрических и непараметрических методах оценки достоверности результатов, их значение и практическое применение. ОЦЕНКА ДОСТОВЕРНОСТИ РЕЗУЛЬТАТОВ СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ Задачей статистического исследования является выявление закономерностей, лежащих в природе исследуемых явлений. Показатели и средние величины должны служить отображением действительности, для чего необходимо определять степень их достоверности. Правильное отображение выборочной совокупностью генеральной совокупности называется репрезентативностью. Мерой точности и достоверности выборочных статистических величин являются средние ошибки представительности (репрезентативности), которые зависят от численности выборки и степени разнообразия выборочной совокупности по исследуемому признаку. Поэтому для определения степени достоверности результатов статистического исследования необходимо для каждой относительной и средней величины вычислить соответствующую среднюю ошибку. Средняя ошибка показателя mp вычисляется по формуле:  При числе наблюдений менее 30  , гдеP — величина показателя в процентах, промилле и т.д. q — дополнение этого показателя до 100, если он в процентах, до 1000, если %0 и т.д. (т.е. q = 100–P, 1000–P и т.д.) Например, известно, что в районе в течение года заболело дизентерией 224 человека. Численность населения ― 33000. Показатель заболеваемости дизентерией на  Средняя ошибка этого показателя  Для решения вопроса о степени достоверности показателя определяют доверительный коэффициент (t), который равен отношению показателя к его средней ошибке, т.е.  В нашем примере  Чем выше t, тем больше степень достоверности. При t=1, вероятность достоверности показателя равна 68,3%, при t=2 ― 95,5%, при t=3 ― 99,7%. В медико-статистических исследованиях обычно используют доверительную вероятность (надежность), равную 95,5%–99,0%, а в наиболее ответственных случаях – 99,7%. Таким образом в нашем примере показатель заболеваемости достоверен. При числе наблюдений менее 30, значение критерия определяется по таблице Стьюдента. Если полученная величина будет выше или равна табличной ― показатель достоверен. Если ниже ― не достоверен. При необходимости сравнения двух однородных показателей достоверность их различий определяется по формуле:  (от большего числа отнимают меньшее),где P1–P2 ― разность двух сравниваемых показателей,  ― средняя ошибка разности двух показателей.Например, в районе Б в течении года заболело дизентерией 270 человек. Население района ― 45000. Отсюда заболеваемость дизентерией:    т.е. показатель заболеваемости достоверен.Как видно, заболеваемость в районе Б ниже, чем в районе А. Определяем по формуле достоверность разницы двух показателей:  При наличии большого числа наблюдений (более 30) разность показателей является статистически достоверной, если t = 2 или больше. Таким образом, в нашем примере заболеваемость в районе А достоверно выше, т.к. доверительный коэффициент (t) больше 2. Зная величину средней ошибки показателя, можно определить доверительные границы этого показателя в зависимости от влияния причин случайного характера. Доверительные границы определяются по формуле:  , гдеP ― показатель; m ― его средняя ошибка; t ― доверительный коэффициент выбирается в зависимости от требуемой величины надежности: t=1 соответствует надежности результата в 68,3% случаев, t=2 – 95,5%, t=2,6 – 99%, t=3 – 99,7%, t=3,3 – 99,9Величина  называется предельной ошибкой.Например, в районе Б показатель заболеваемости дизентерией с точностью до 99,7  т.е. от 49,1 до 70,9 .Также, как и для относительных величин необходимо для средней арифметической определять ее среднюю ошибку. Средняя ошибка средней арифметической mx ― определяется по формуле:  или  (при числе наблюдений менее 30), где ― среднее квадратичное отклонение;n ― число наблюдений. Определение средней ошибки средней арифметической необходимо: 1. Для оценки достоверности средней арифметической, которая определяется по формуле:  2. Для определения достоверности разности двух средних арифметических, которая определяется по формуле:  В обоих случаях оценка производится так же, как и при определении достоверности показателей, т.е. при числе наблюдений более 30 результаты достоверны, если величина доверительного коэффициента (t) равна или больше 2. 3. Для определения доверительных границ средней арифметической, т.е. в каких пределах может колебаться средняя арифметическая в зависимости от случайных факторов. Например, обследовано 15 рабочих в цехе с высокой температурой окружающего воздуха на частоту пульса. Результаты:
15 1220 382,2 Определить среднюю частоту пульса и ее достоверность. Вначале по формуле определяем среднюю арифметическую  уд. в мин.По формуле определяем среднее квадратичное отклонение 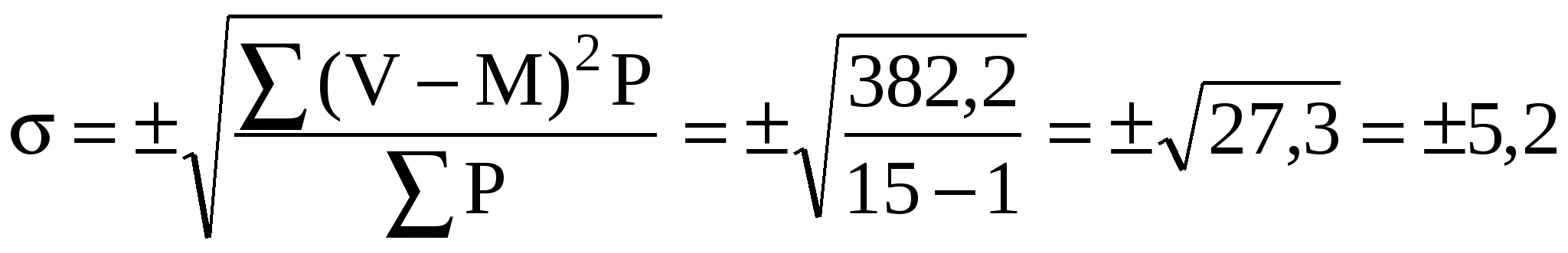 Затем по формуле вычисляем среднюю ошибку средней арифметической  Для оценки степени достоверности средней арифметической полученные данные подставляем в формулу  Величина достоверна. Допустим известно, что в цехе с нормальной температурой окружающего воздуха (18―200) при обследовании 25 рабочих установлена средняя частота пульса 72,4 уд. в мин. Среднее квадратичное отклонение ― 4,8 уд. в мин, средняя ошибка 0,96. Требуется определить достоверность разности в частоте пульса у рабочих обоих цехов. Для этого данные подставляем в формулу  Разница в частоте ударов пульса у рабочих сравниваемых цехов статистически достоверна. Наконец, определяем доверительные границы частоты пульса у рабочих в цехе с высокой температурой окружающего воздуха со степенью вероятности 99,7 %.  т.е. от 77,1 до 85,5 уд. в мин.ИЗМЕРЕНИЕ СВЯЗИ МЕЖДУ ЯВЛЕНИЯМИ Все явления в природе и обществе находятся во взаимной связи. По характеру зависимости явлений различают: функциональную (полную); корреляционную (неполную) связи. Функциональная связь означает строгую зависимость явлений, когда любому значению одного из них всегда соответствует определенное одно и тоже значение другого. Функциональная связь обычно выражается формулами: (Объем тела  ;  и т.д.)При корреляционной же связи одной и той же величине одного признака соответствуют разные величины другого. Например: между ростом и весом имеется корреляционная связь, между заболеваемостью злокачественными новообразованиямии возрастом и т.д. По направлению различают прямые и обратные корреляционные связи. При прямой ― увеличение одного из признаков ведет к увеличению другого; при обратном же ― с увеличением одного признака второй уменьшается. По силе связь может быть сильной, средней и слабой. На основе статистического анализа можно установить наличие связи, ее направление и измерить ее силу. Одним из способов измерения связи между явлениями является вычисление коэффициента корреляции, который обозначается rху. Он может быть вычислен различными способами. Наиболее точным является метод квадратов (Пирсона), при котором коэффициент корреляции определяется по формул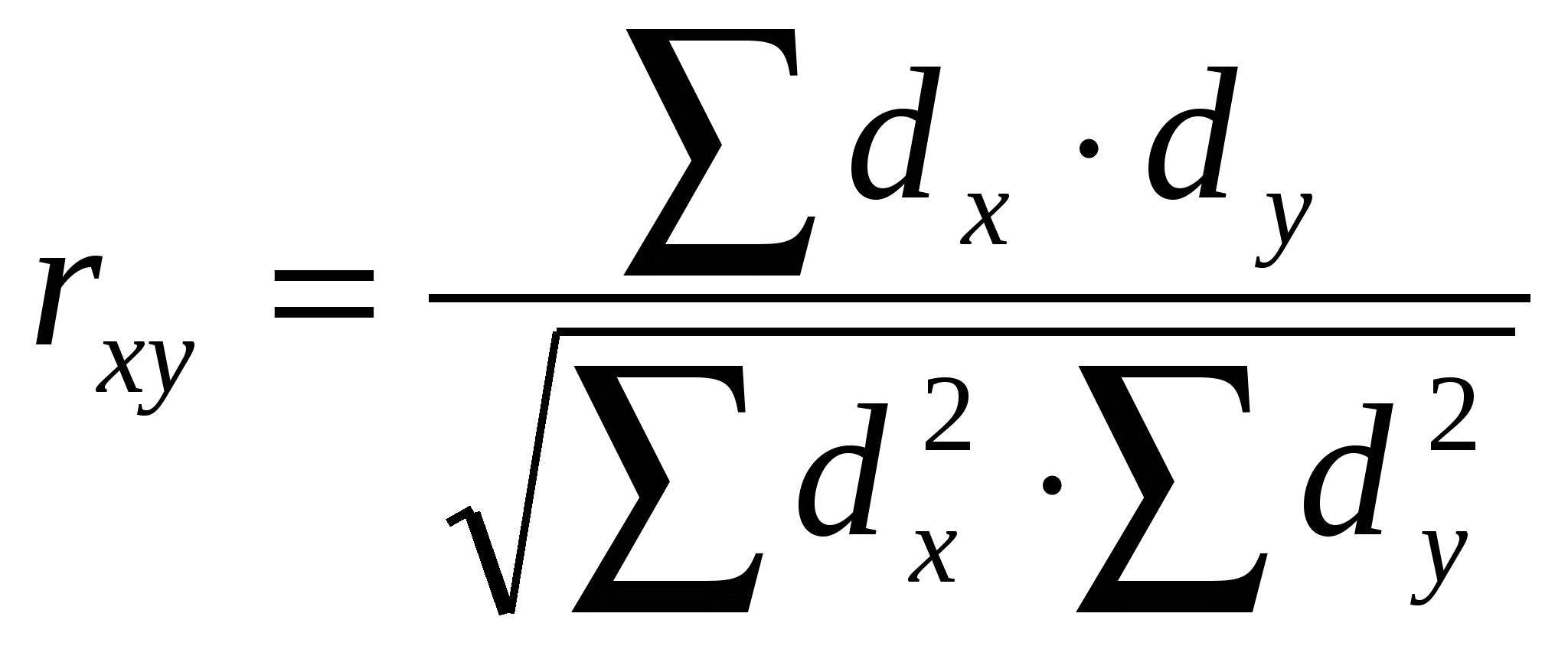е:  , гдеrху ― коэффициент корреляции между статистическим рядом X и Y. dх ― отклонение каждого из чисел статистического ряда X от своей средней арифметической. dу ― отклонение каждого из чисел статистического ряда Y от своей средней арифметической. В зависимости от силы связи и ее направления коэффициент корреляции может находиться в пределах от 0 до 1 (-1). Коэффициент корреляции, равный 0, говорит о полном отсутствии связи. Чем ближе уровень коэффициента корреляции к 1 или (-1), тем соответственно больше, теснее измеряемая им прямая или обратная связь. При коэффициенте корреляции равном 1 или (-1) связь полная, функциональная. Схема оценки силы корреляционной связи по коэффициенту корреляции
Для вычисления коэффициента корреляции по методу квадратов составляется таблица из 7 колонок. Разберем процесс вычисления на примере: ОПРЕДЕЛИТЬ СИЛУ И ХАРАКТЕР СВЯЗИ МЕЖДУ СОДЕРЖАНИЕМ ЙОДА В ВОДЕ И ПОРАЖЕННОСТЬЮ ЗОБОМ:
1. Определяем среднее содержание йода в воде (в мг/л).  мг/л2.Определяем среднюю пораженность зобом в %.  3. Определяем отклонение каждого Vx от Мx, т.е. dx. 201–138=63; 178–138=40 и т.д. 4. Аналогично определяем отклонение каждого Vу от Mу, т.е. dу. 0,2–3,8=-3,6; 0,6–38=-3,2 и т.д. 5. Определяем произведения отклонений. Полученное произведение суммируем и получаем.  6. dх возводим в квадрат и результаты суммируем, получаем.  7. Аналогично возводим в квадрат dу, результаты суммируем, получим  8. Наконец, все полученные суммы подставляем в формулу:  Для решения вопроса о достоверности коэффициента корреляции определяют его среднюю ошибку по формуле:  (Если число наблюдений менее 30, тогда в знаменателе n–1). В нашем примере  Величина коэффициента корреляции считается достоверной, если не менее чем в 3 раза превышает свою среднюю ошибку. В нашем примере  Таким образом, коэффициент корреляции не достоверен, что вызывает необходимость увеличения числа наблюдений. Коэффициент корреляции можно определить несколько менее точным, но намного более легким способом ― методом рангов (Спирмена). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||