1. озз. Определение, разделы дисциплины, задачи, структура. Роль дисциплины в системе мед образования, практической деятельности врачаспециалиста и организаций здравоохранения
 Скачать 2.59 Mb. Скачать 2.59 Mb.
|
|
15 1220 382,2 Определить среднюю частоту пульса и ее достоверность. Вначале по формуле определяем среднюю арифметическую По формуле определяем среднее квадратичное отклонение 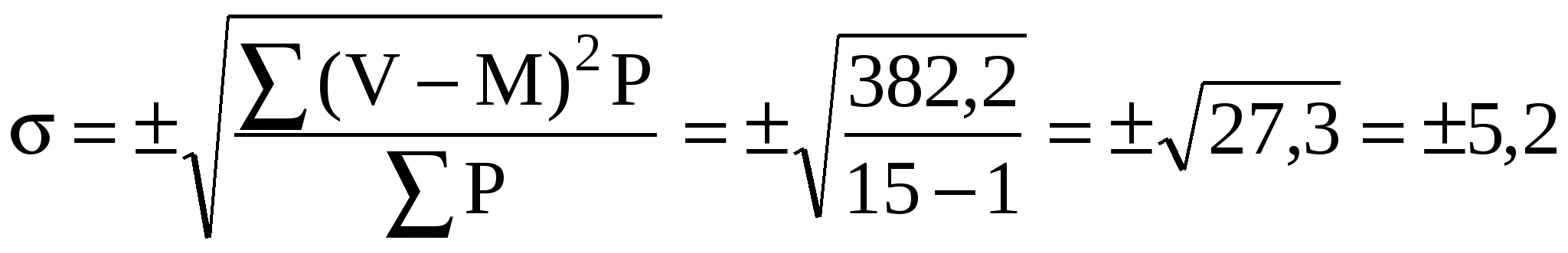 Затем по формуле вычисляем среднюю ошибку средней арифметической Для оценки степени достоверности средней арифметической полученные данные подставляем в формулу Величина достоверна. Допустим известно, что в цехе с нормальной температурой окружающего воздуха (18―200) при обследовании 25 рабочих установлена средняя частота пульса 72,4 уд. в мин. Среднее квадратичное отклонение ― 4,8 уд. в мин, средняя ошибка 0,96. Требуется определить достоверность разности в частоте пульса у рабочих обоих цехов. Для этого данные подставляем в формулу Разница в частоте ударов пульса у рабочих сравниваемых цехов статистически достоверна. Наконец, определяем доверительные границы частоты пульса у рабочих в цехе с высокой температурой окружающего воздуха со степенью вероятности 99,7 %. ИЗМЕРЕНИЕ СВЯЗИ МЕЖДУ ЯВЛЕНИЯМИ Все явления в природе и обществе находятся во взаимной связи. По характеру зависимости явлений различают: функциональную (полную); корреляционную (неполную) связи. Функциональная связь означает строгую зависимость явлений, когда любому значению одного из них всегда соответствует определенное одно и тоже значение другого. Функциональная связь обычно выражается формулами: (Объем тела При корреляционной же связи одной и той же величине одного признака соответствуют разные величины другого. Например: между ростом и весом имеется корреляционная связь, между заболеваемостью злокачественными новообразованиямии возрастом и т.д. По направлению различают прямые и обратные корреляционные связи. При прямой ― увеличение одного из признаков ведет к увеличению другого; при обратном же ― с увеличением одного признака второй уменьшается. По силе связь может быть сильной, средней и слабой. На основе статистического анализа можно установить наличие связи, ее направление и измерить ее силу. Одним из способов измерения связи между явлениями является вычисление коэффициента корреляции, который обозначается rху. Он может быть вычислен различными способами. Наиболее точным является метод квадратов (Пирсона), при котором коэффициент корреляции определяется по формуле: 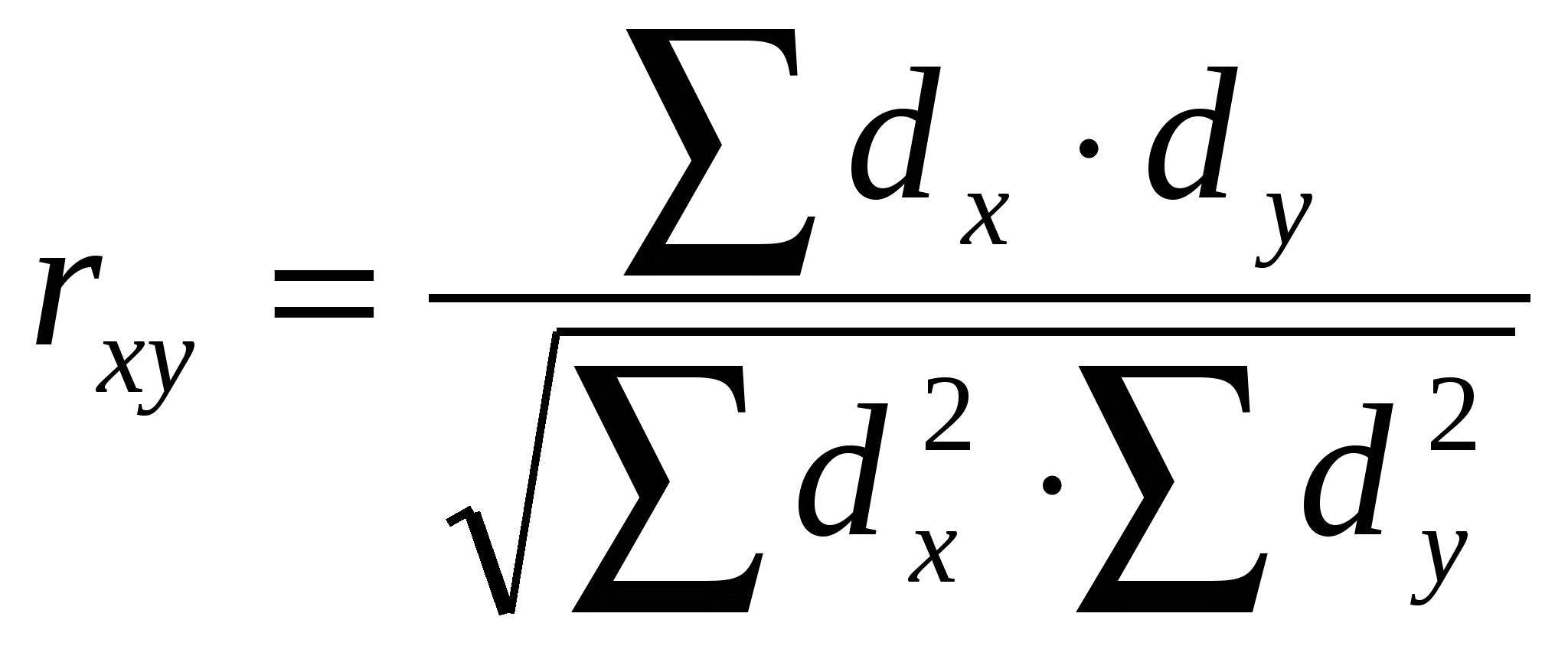 , где , гдеrху ― коэффициент корреляции между статистическим рядом X и Y. dх ― отклонение каждого из чисел статистического ряда X от своей средней арифметической. dу ― отклонение каждого из чисел статистического ряда Y от своей средней арифметической. В зависимости от силы связи и ее направления коэффициент корреляции может находиться в пределах от 0 до 1 (-1). Коэффициент корреляции, равный 0, говорит о полном отсутствии связи. Чем ближе уровень коэффициента корреляции к 1 или (-1), тем соответственно больше, теснее измеряемая им прямая или обратная связь. При коэффициенте корреляции равном 1 или (-1) связь полная, функциональная. Схема оценки силы корреляционной связи по коэффициенту корреляции
Для вычисления коэффициента корреляции по методу квадратов составляется таблица из 7 колонок. Разберем процесс вычисления на примере: ОПРЕДЕЛИТЬ СИЛУ И ХАРАКТЕР СВЯЗИ МЕЖДУ СОДЕРЖАНИЕМ ЙОДА В ВОДЕ И ПОРАЖЕННОСТЬЮ ЗОБОМ:
1. Определяем среднее содержание йода в воде (в мг/л). 2.Определяем среднюю пораженность зобом в %. 3. Определяем отклонение каждого Vx от Мx, т.е. dx. 201–138=63; 178–138=40 и т.д. 4. Аналогично определяем отклонение каждого Vу от Mу, т.е. dу. 0,2–3,8=-3,6; 0,6–38=-3,2 и т.д. 5. Определяем произведения отклонений. Полученное произведение суммируем и получаем. 6. dх возводим в квадрат и результаты суммируем, получаем. 7. Аналогично возводим в квадрат dу, результаты суммируем, получим 8. Наконец, все полученные суммы подставляем в формулу: Для решения вопроса о достоверности коэффициента корреляции определяют его среднюю ошибку по формуле: (Если число наблюдений менее 30, тогда в знаменателе n–1). В нашем примере Величина коэффициента корреляции считается достоверной, если не менее чем в 3 раза превышает свою среднюю ошибку. В нашем примере Таким образом, коэффициент корреляции не достоверен, что вызывает необходимость увеличения числа наблюдений. Коэффициент корреляции можно определить несколько менее точным, но намного более легким способом ― методом рангов (Спирмена). СТАНДАРТИЗОВАННЫЕ ПОКАЗАТЕЛИ При анализе материалов о здоровье населения, деятельности лечебно- профилактических организаций, качестве оказания медицинской помощи, эффективности лечебных и оздоровительных мероприятий применяется сравнение общих интенсивных показателей или средних величин. Но это сравнение дает истинный результат лишь в тех случаях, если показатели вычислены в отношении качественно однородной совокупности (по возрасту, полу, профессии и т.д.), поскольку на величину общих интенсивных показателей влияет не только разная санитарная обстановка или качество лечебно-профилактической работы, но и различие в возрастном, половом, профессиональном, социальном составе сравниваемых групп населения. Наибольшее влияние на уровень многих показателей оказывает возрастной состав населения. Так, известно, что наиболее высокие показатели заболеваемости и смертности отмечаются у детей и стариков. Ниже у лиц молодого и среднего возраста. Следовательно, там, где в составе населения больше детей и стариков, уровень заболеваемости и смертности бывает выше, даже если санитарные условия и медицинская помощь лучше. Подтверждением сказанному может быть следующий пример: ЛЕТАЛЬНОСТЬ ОТ ОЧАГОВОЙ ПНЕВМОНИИ В ДВУХ ДЕТСКИХ БОЛЬНИЦАХ
Как видно из таблицы, в больнице № 1 общий показатель летальности выше, чем в больнице № 2, несмотря на то, что повозрастные показатели ниже. Объясняется это тем, что состав больных по возрасту в сравниваемых больницах различен: в больнице № 1 детей в возрасте до 3 лет лечилось 60%, а в больнице № 2 только 20%, а дети младшего возраста имеют более высокие показатели летальности. Поэтому на основании общих показателей летальности можно делать выводы при сравнении двух больниц лишь при условии однородного состава отделений, примерно одинакового состава больных и т.д. В тех же случаях, когда приходится сравнивать интенсивные показатели в двух совокупностях, состав которых не одинаков, правильные выводы могут быть получены только на основании специально вычисляемых показателей. Статистический метод, позволяющий исключить (элиминировать) влияние неоднородного состава сравниваемых групп на общие показатели, называется методом стандартизации. В результате использования этого метода получаются стандартизованные показатели, т.е. условные, которые могли бы быть при условии однородного состава. Показатели эти применяются только в целях сравнения. При изменении стандарта меняется и величина стандартизованных показателей, поэтому при анализе важны не их абсолютные величины, а степень различия стандартизованных показателей между собой. В зависимости от наличия исходных данных можно пользоваться одним из трех методов стандартизации: прямым, косвенным или обратным. Прямой метод стандартизации― наиболее распространенный. Стандартизованные показатели вычисляются прямым методом, когда известны: ― состав совокупности (населения, работающих, больных). ― состав изучаемого явления по этим же группам. Стандартизация проводится в следующей последовательности: 1. Вычисление групповых показателей. 2. Выбор и вычисление стандарта. В качестве стандарта можно взять: ― состав одной из сравниваемых групп; ― средний состав или состав обеих групп, взятых вместе; ― состав третьего объекта, известного по предыдущим исследованиям или по другим материалам. Желательно состав третьего объекта брать тот, в состав которого входят сравниваемые группы. Например, при сравнении заболеваемости или смертности в двух районах за стандарт целесообразно взять возрастной состав населения области, республики. 3. Вычисление «ожидаемых» чисел изучаемого явления в сравниваемых совокупностях по стандарту. 4. Определение стандартизованных показателей и выводы. Сущность прямого метода состоит в том, что условно принимают какой-либо состав населения или больных за стандарт и считают его одинаковым в сравниваемых совокупностях. Затем, учитывая действительные размеры явления по групповым показателям, вычисляют стандартизованные коэффициенты. Прямой метод стандартизации состоит из следующих этапов: I этап – вычисление интенсивных показателей. В нашем примере – вычисление частоты случаев нетрудоспособности в целом по цехам и в каждой возрастной группе: Рассчитываем общий интенсивный показатель для цеха № 1: 1000 работающих – 1345 случаев 100 работающих - х I этап прямого метода стандартизации
В возрасте до 19 лет (для цеха № 1) – частный интенсивный показатель: 120 работающих – 80 случаев 100 работающих - х II этап прямого способа стандартизации – выбор стандарта. За стандарт обычно берут распределение по устраняемому фактору одной из сред, либо их сумму, либо подсумму. Однако, стандарт можно выбрать любой, по нашему смотрению. В нашем примере за стандарт можно взять распределение работающих в цехе № 1, либо в цехе № 2, либо средний возрастной состав по цехам № 1 и № 2, либо любое другое распределение работающих по возрасту. Пусть за стандарт мы возьмем сумму работающих в обоих цехах, т.е. в возрасте до 19 лет: 120 + 200 = 320 работающих, в 20-39 лет – 380 + 500 = 880 работающих и т.д. III этап – наиболее ответственный – вычисление ожидаемых чисел. Необходимо вычислить, какова была бы величина сравниваемого явления, если бы частные интенсивные показатели остались прежними, а распределение среды было бы таким, как по стандарту. В нашем примере вычисляем, сколько было бы случаев нетрудоспособности в цехе № 1 и № 2. если бы повозрастные показатели работающих в каждой возрастной группе было бы таким, как по стандарту и одинаковым (что очень важно) в цехе № 1 и № 2. Найдем сколько случаев нетрудоспособности было бы у работающих в возрасте до 19 лет в цехе № 1: на 100 работающих – 66,7 случаев на 320 работающих - х случаев 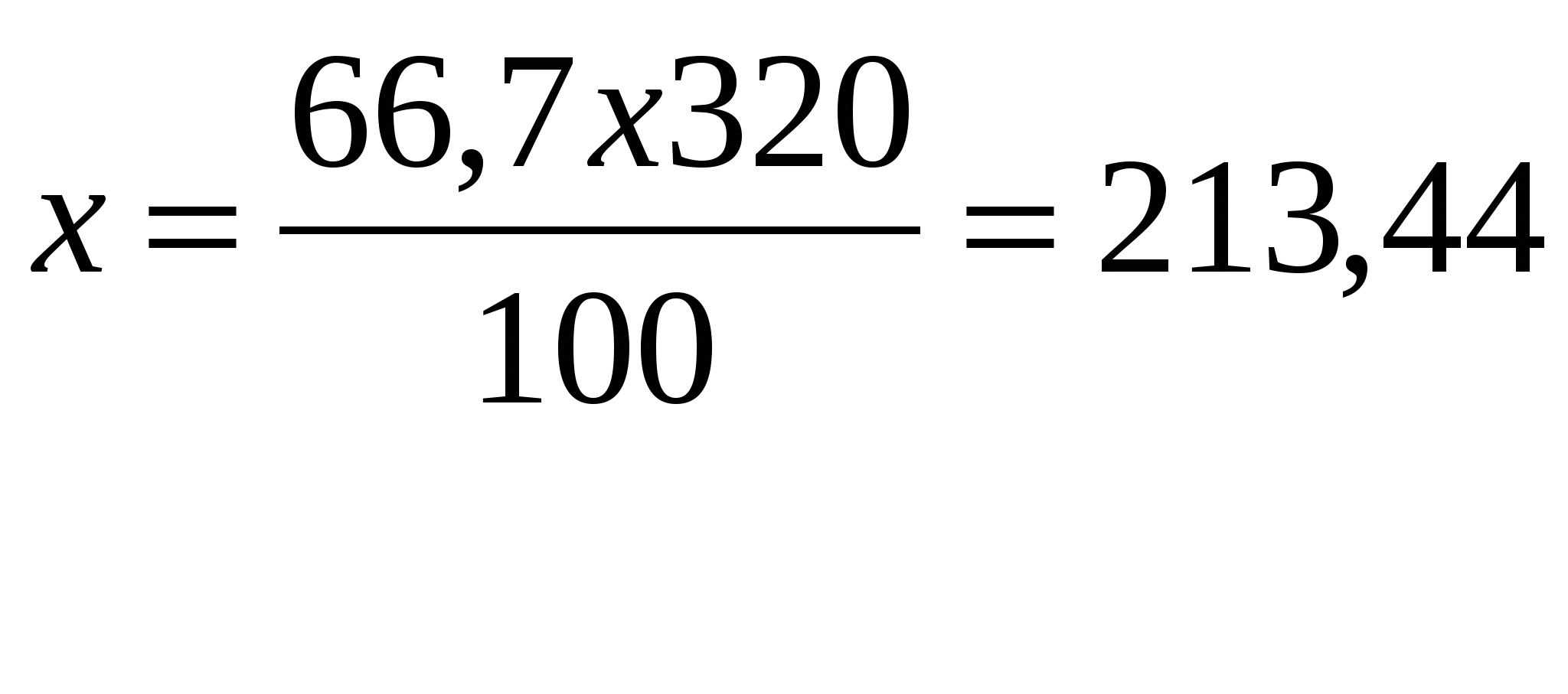 В том же цехе № 1 в возрасте 20-39 лет число случаев нетрудоспособности составило бы: на 100 работающих – 105,3 случая на 880 работающих - х IV этап – вычисление стандартизованных показателей и их сравнение. Стандартизованные показатели рассчитываются, как и обычные интенсивные показатели, на величину стандарта. В нашем примере рассчитываем частоту случаев нетрудоспособности на 100 рабочих. В цехе № 1 на 1800 работающих было бы всего 2178,1 случаев нетрудоспособности, следовательно, на 100 работающих – х. В цехе № 2: Выводы: если бы возрастной состав работающих в цехах был одинаковым, то частота случаев заболеваемости в цехе № 2 была бы выше, чем в цехе № 1. Более высокий интенсивный показатель частоты случаев нетрудоспособности в цехе № 1 (134,5) обусловлен тем, что в нем среди работающих лиц старше 40 лет составляют 50%, а в цехе № 2 – только 12,5%. Стандартизованные показатели могут быть использованы только для сравнения, их величина является условной, зависящей от выбора условий (стандарта), она не дает представления об истинном размере того или иного явления. Поэтому указывать величину стандартизованного показателя не следует. На основании сравнения стандартизованных показателей можно судить, где выше или ниже величина явления при условии устранения влияния на него неоднородного состава сравниваемых совокупностей или (проще), как соотносились бы интенсивные показатели при устранении влияния на них определенного фактора. Косвенный метод применяется при отсутствии данных о распределении изучаемого явления или очень малых числах при этом распределении. Для проведения стандартизации по этому методу нужны следующие данные: —распределение совокупности по составу (населения по возрасту рабочих, по стажу работы и т.д.). —общая численность изучаемого явления (число заболевших, умерших и т.п.) —погрупповые интенсивные показатели, которые можно принять за стандарт (по области, республике и др). Обратный методприменяется при отсутствии сведений о составе сравниваемых совокупностей. Для проведения стандартизации этим методом требуются данные: —состав изучаемого в обоих совокупностях явления (больных, умерших и т.п.). —общая численность сравниваемых совокупностей (населения, рабочих т.п.). —погрупповые интенсивные показатели, которые можно взять за стандарт (по области, республике и др). Последовательность вычисления косвенного и обратного методов: —выбор стандарта. —вычисление «ожидаемых» численностей обоих совокупностей (населения, больных). —вычисление стандартизованных показателей. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
