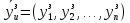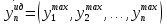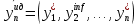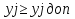Модуль 3. 1. Память эвм, ее характеристики. Структура памяти. Постоянные запоминающие устройства (программируемые маской, перепрограммируемые eprom, eeprom). Оперативные запоминающие устройства статического и динамического типов. Стек. Виртуальная память

• Название: 1. Память эвм, ее характеристики. Структура памяти. Постоянные запоминающие устройства (программируемые маской, перепрограммируемые eprom, eeprom). Оперативные запоминающие устройства статического и динамического типов. Стек. Виртуальная память
• Анкор: Модуль 3.docx
• Дата: 20.03.2019
• Размер: 2.32 Mb.
• Имя файла: Модуль 3.docx
• Тип: Документы; #26201
• страница: 10 из 12

Определение области компромиссов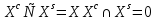

Xc – область компромиссов

Xs – область согласия

В область согласия входят решения, для любого из которых можно найти решение из области компромиссов, превосходящее его по всем критериям. Для решений составляющих область компромиссов характерно то, что хотя-бы по одному критерию одно решение превосходит другое.

Идея алгоритма: выбирается х1 из Х, выбирается другой х2 из Х и производится сравнение х1 и х2. Результаты:

х1>x2 по всем критериям, тогда х2 отправляем в область согласия, исключаем из Х и выбираем х3

х1<х2 по всем критериям, тогда x1 отправляем в область согласия, исключаем из Х и выбираем х3

если по разным критериям различные результаты, то берём х3 из Х

Алгоритм прост и основан на переборе и сравнении.

Нормализация критериев

Под нормализацией понимается процедура искусственного приведения критериев к единой мере и масштабу измерения.

А) безразмерные

Б)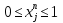

Идеальный критерий :

1. 
   
   
2. 
   максимальный на заданном множестве решений
   
3. 
   супремум и инфимум
   

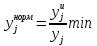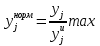Для нормализованного критерия, чем больше, тем лучше.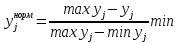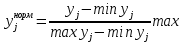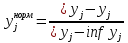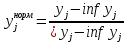





2 принцип выделения главного критерия

1. 
   для всех критериев задаются их допустимые значения. Из множества компромисов выбирается такой, для которого все
   
2. 
   для выбранного главного критерия определяется решение yопт, которое принадлежит y’
   

Принципы оптимальности многовекторных задач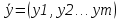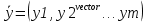

Нужно использовать свои принципы оптимальности на каждом уровне и в конечном счёте вектор в основной задаче необходимо заменить числом.

Скаляризация – переход от вектор задачи к скалярной.

Характеристики приоритета критериев и методы его учёта

Характеристики приоритета:

1. 
   Ряд приоритета – упорядоченное множество индексов локальных критериев Y=(1,2,3…m). Y1>y2>y3… если критерии равноценны, то они выделяются.
   
2. 
   Вектор приоритета – вектор, компонентами которого служит бинарное отношение приоритета, который определяет степень превосходства двух соседних критериев. λ=( λ1, λ2… λm). Все от 1 до бесконечности. Первый лучше второго в значение раз.
   
3. 
   Весовой вектор v=(v1,v2,,,,vm), 0<=vj<=1. Сумма равна 1. Λi=vi/vi+1. Vk=П λi/СУММ Пk λi
   

Методы учёта приоритета критериев

Принцип жесткого приоритета. Критерии расположены в ряд приоритета. При выборе решения не разрешается повышать уровень менее важных критериев, если это приводит к понижению уровня более важных критериев.

Принцип последовательной уступки. Имеется ряд приоритетов критериев. По наиболее важному критерию назначается уступка по наиболее важному критерию назначается уступка Δy1 и выбирается решение из [y1,y1-Δy1]. Выбирается решение y2 и выбирается вторая уступка Δy2 и выбирается…. И так далее до получения действенного решения.

Методы учёта гибкого приоритета. v1*y1;v2*y2;v3*y3. Переходим к нормализованной таблице, но с учётом весов.