1. Понятие о статистике 3
 Скачать 4.08 Mb.
|
|
7. Подбор уравнения регрессии45 представляет собой математическое описание изменения взаимно коррелируемых величин по эмпирическим (фактическим) данным. Уравнение регрессии должно определить, каким будет среднее значение результативного признака у при том или ином значении факторного признака х, если остальные факторы, влияющие на у и не связанные с х, не учитывать, т.е. абстрагироваться от них. Другими словами, уравнение регрессии можно рассматривать как вероятностную гипотетическую функциональную связь величины результативного признака у со значениями факторного признака х. Уравнение регрессии можно также назвать теоретической линией регрессии. Рассчитанные по уравнению регрессии значения результативного признака называются теоретическими.Они обычно обозначаются  или  (читается: «игрек, выравненный по х») и рассматриваются как функция от х, т.е.  = f(x).Найти в каждом конкретном случае тип функции, с помощью которой можно наиболее адекватно отразить ту или иную зависимость между признаками х и у, — одна из основных задач регрессионного анализа. Выбор теоретической линии регрессии часто обусловлен формой эмпирической линии регрессии; теоретическая линия как бы сглаживает изломы эмпирической линии регрессии. Кроме того, необходимо учитывать природу изучаемых показателей и специфику их взаимосвязей. Для аналитической связи между х и у могут использоваться виды уравнений, приведенные в таблице 30 (при условии замены t на x). Обычно зависимость, выражаемую уравнением прямой, называют линейной (или прямолинейной), а все остальные — криволинейными зависимостями. Выбрав тип функции (таблица 30), по эмпирическим данным определяют параметры уравнения. При этом отыскиваемые параметры должны быть такими, при которых рассчитанные по уравнению теоретические значения результативного признака были бы максимально близки к эмпирическим данным.Существует несколько методов нахождения параметров уравнения регрессии. Наиболее часто используется метод наименьших квадратов (МНК). Его суть заключается в следующем требовании: искомые теоретические значения результативного признака должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических значений, т.е. .Поставив данное условие, легко определить, при каких значениях a0, a1 и т.д. для каждой аналитической кривой эта сумма квадратов отклонений будет минимальной. Данный метод уже использовался нами в теме 6 «Статистическое изучение динамики ВЭД», поэтому, воспользуемся формулой (100) для нахождения параметров теоретической линии регрессии, заменив параметр t на x: 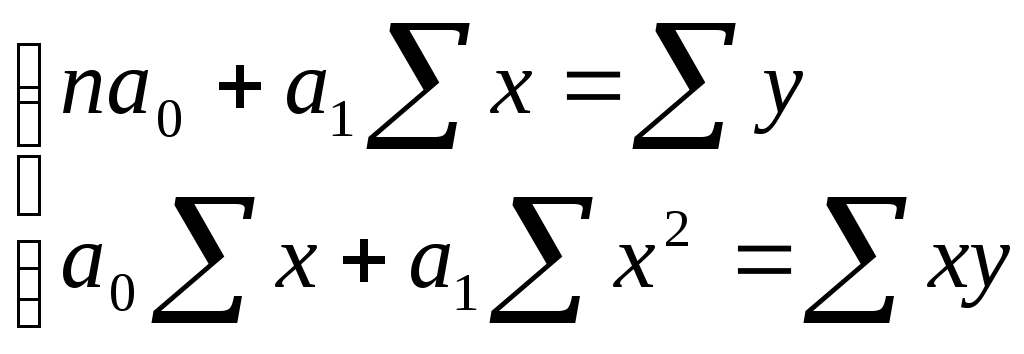 (133)Выразив из первого уравнения системы (133) a0, получим46:  . (134)Подставив (134) во второе уравнение системы (133), затем разделив обе его части на n, получим:  . (135)Применяя 3 раза формулу средней арифметической, получим:  . (136)Раскрыв скобки и перенеся члены без a1 в правую часть уравнения, выразимa1:  . (137)Параметр a1 в уравнении линейной регрессии называется коэффициентом регрессии, который показывает на сколько изменяется значение результативного признака y при изменении факторного признака x на единицу. Исходные данные и расчеты для нашего примера представим в таблице 45. Таблица 45. Вспомогательные расчеты для нахождения уравнения регрессии
По формуле (137):  = 5,407.По формуле (134): a0 = 238,674 – 5,407*36,602 = 40,767. Отсюда получаем уравнение регрессии: 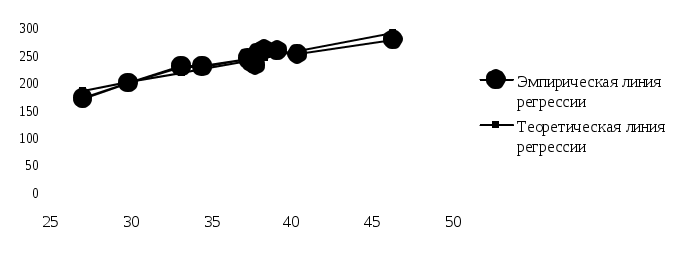 =40,767+5,407x, подставляя в которое вместо x эмпирические значения факторного признака (2-й столбец таблицы 45), получаем выравненные по прямой линии теоретические значения результативного признака (6-й столбец таблицы 45)47. Для иллюстрации различий между эмпирическими и теоретическими линиями регрессии построим график (рисунок Error: Reference source not found). Рис. 22. График эмпирической и теоретической линий регрессии Из рисунка 22 видно, что небольшие различия между эмпирической и теоретической линиями регрессии существуют, поэтому необходимо оценить существенность коэффициента регрессии и уравнения связи, для чего определяют среднюю ошибку параметров уравнения регрессии и сравнивают их с этой ошибкой. Расчет ошибок параметров уравнения регрессии основан на использовании остаточной дисперсии, характеризующей расхождение (отклонение) между эмпирическими и теоретическими значениями результативного признака. Для линейного уравнения регрессии (  ) средние ошибки параметров a1 и a2 определяются по формулам (138) и (139) соответственно: , (138)  , (139)  . (140)Значимость параметров проверяется путем сопоставления его значения со средней ошибкой. Обозначим это соотношение как t:  , (141)При большом числе наблюдений (n>30) параметр ai считается значимым, если  >3.Если выборка малая (n<30), то значимость параметра ai проверяется путем сравнения с табличным значения t-критерия Стьюдента при числе степеней свободы ν=n-2 и заданном уровне значимости α (Приложение 2). Если рассчитанное по формуле (141) значение больше табличного, то параметр считается значимым. В нашем примере по формуле (140):  = 9,669.Находим среднюю ошибку параметра a0 по формуле (138):  = 3,06.Теперь находим среднюю ошибку параметра a1 по формуле (139):  =0,639.Теперь по формуле (141) для параметра a0:  =13,3.И по той же формуле для параметра a1:  =8,46.Так как выборка малая, то задавшись стандартной значимостью α=0,05 находим в 10-й строке Приложения 2 табличное значение tα=2,23, которое значительно меньше полученных значений 13,3 и 8,46, что свидетельствует о значимости обоих параметров уравнения регрессии. Наряду с проверкой значимости отдельных параметров осуществляется проверка значимости уравнения регрессии в целом или, что то же самое, проверка адекватности модели с помощью критерия Фишера по Приложению 4. Данный метод уже использовался нами для проверки адекватности уравнения тренда в предыдущей теме, поэтому воспользовавшись формулой (102) в нашем примере получим48:  Сравнивая расчетное значение критерия Фишера Fр = 71,56 с табличным Fт = 4,96, определяемое по Приложению 4 при числе степеней свободы ν1 = k– 1 = 2 –1 = 1 и ν2 = n– k= 12 – 2 = 10 (т.е. 1-й столбец и 10-я строка) и стандартном уровне значимости α=0,05, можно сделать вывод, что уравнение регрессии значимо. 8. Коэффициент эластичности показывает, на сколько процентов изменяется в среднем результативный признак y при изменении факторного признака x на 1%. Он рассчитывается на основе уравнения регрессии:  , (142)где  – первая производная уравнения регрессии y по x.Коэффициент эластичности – величина переменная, т.е. изменяется с изменением значений фактора x. Так, для линейной зависимости  : . (143)Применительно к рассмотренному уравнению регрессии, выражающему зависимость величины таможенных платежей в федеральный бюджет от величины стоимостного внешнеторгового оборота ( = 40,767 + 5,407x), коэффициент эластичности по формуле (143):  . Подставляя в данное выражение разные значения x, получаем и разные значения Э. Так, например, при x = 40 коэффициент эластичности  = 0,84, а при x = 50 соответственно  = 0,87 и т.д. Это значит, что при увеличении внешнеторгового товарооборота x с 40 до 40,4 млрд.долл. (т.е. на 1%), величина таможенных платежей возрастет в среднем на 0,84% прежнего уровня; при увеличении x с 50 до 50,5 млрд.долл. (т.е. на 1%) y возрастет на 0,87% и т.д. 9. Теоретическое корреляционное отношение как универсальный показатель тесноты связи. Измерить тесноту связи между коррелируемыми величинами – значит определить, насколько вариация результативного признака обусловлена вариацией факторного (факторных) признака. Ранее были рассмотрены показатели, с помощью которых можно выявить наличие корреляционной связи между двумя признаками x и y и измерить тесноту этой связи. Наряду с ними существует универсальный показатель – корреляционное отношение (или коэффициент корреляции по Пирсону), применимое ко всем случаям корреляционной зависимости независимо от формы этой связи. Следует различать эмпирическое и теоретическое корреляционное отношение. Эмпирическое корреляционное отношение рассчитывается на основе правила сложения дисперсий как корень квадратный из отношения межгрупповой дисперсии к общей дисперсии, т.е.  . (144)Теоретическое корреляционное отношение  определяется на основе выравненных (теоретических) значений результативного признака  , рассчитанных по уравнению регрессии. представляет собой относительную величину, получаемую в результате сравнения среднего квадратического отклонения в ряду теоретических значений результативного признака со средним квадратическим отклонением в ряду эмпирических значений. Если обозначить дисперсию эмпирического ряда игреков через  , а теоретического ряда –  , то каждая из них выразится формулами ,  .Сравнивая вторую дисперсию с первой, получим теоретический коэффициент детерминации: 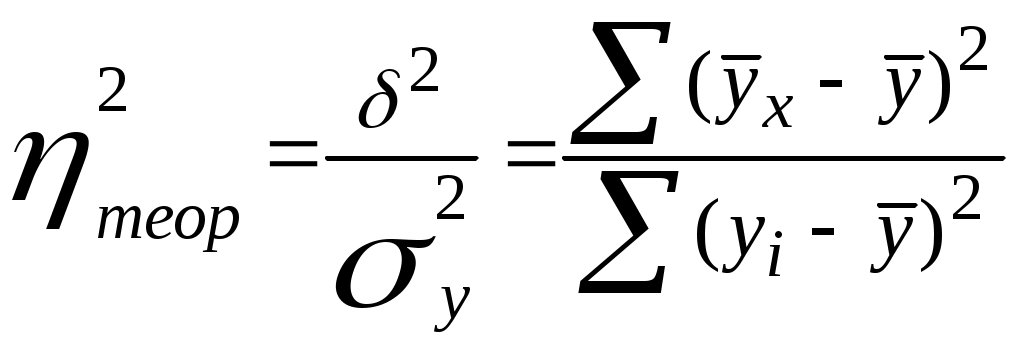 , (145)который показывает, какую долю в общей дисперсии результативного признака занимает дисперсия, выражающая влияние вариации фактора x на вариацию y. Извлекая корень квадратный из коэффициента детерминации, получаем теоретическое корреляционное отношение 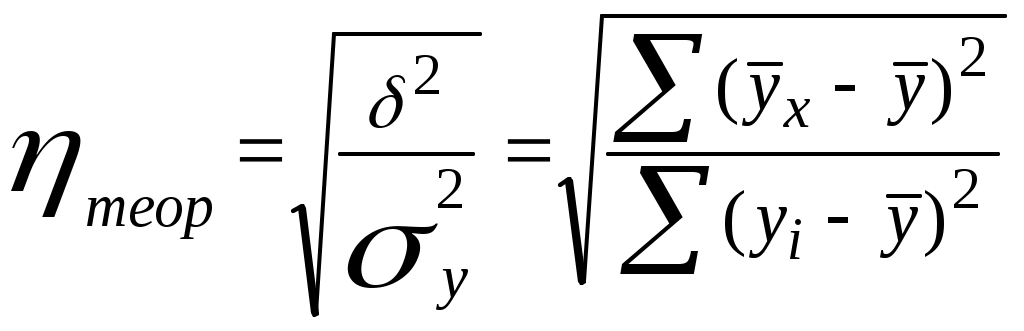 . (146)Оно может находиться в пределах от 0 до 1, чем ближе его значение к 1, тем теснее связь между вариацией y и x. Для оценки тесноты связи обычно применяется шкала Чэддока (таблица 43). Корреляционное отношение применимо как для парной, так и для множественной корреляции независимо от формы связи. В этом смысле его можно назвать универсальным показателем тесноты связи. При линейной зависимости  .Покажем расчет  на условном примере. Исходные данные и расчет дополнительных показателей приведен в таблице 46.Таблица 46. Исходные данные и вспомогательные расчеты для нахождения теоретического корреляционного отношения 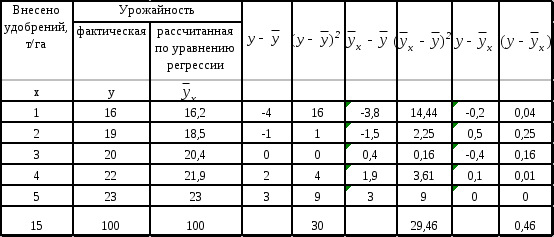 В данном примере общая средняя урожайность:  (ц/га).Общая дисперсия:  =30/5=6, факторная дисперсия: =29,46/5=5,892.Отсюда теоретическое корреляционное отношение: 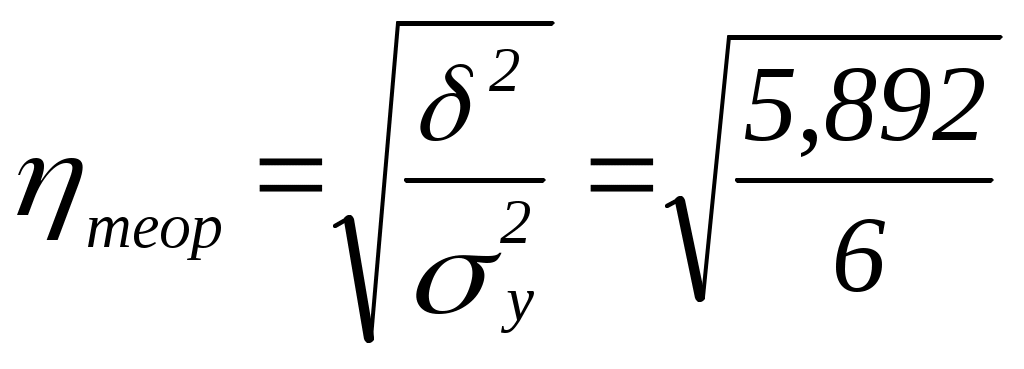 =0,99. Данное значение характеризует очень тесную зависимость изменения урожайности от изменения количества внесенных удобрений. В нашем примере незначительные расхождения (30 29,46+0,46 – это правило сложения дисперсий) объясняются округлением значений параметров уравнения регрессии и самих . |
