1. Понятие о статистике 3
 Скачать 4.08 Mb. Скачать 4.08 Mb.
|
7. Статистическое изучение взаимосвязей7.1. Понятие корреляционной зависимостиОдин из наиболее общих законов объективного мира – закон всеобщей связи и зависимости между явлениями. Естественно, что, исследуя явления в самых различных областях, статистика неизбежно сталкивается с зависимостями как между количественными, так и между качественными показателями, признаками. Ее задача – обнаружить (выявить) такие зависимости и дать им количественную характеристику. Среди взаимосвязанных признаков (показателей) одни могут рассматриваться как определенные факторы, влияющие на изменение других (факторные), а вторые (результативные) – как следствие, результат влияния первых. Существует 2 вида связи между отдельными признаками: функциональная и стохастическая (статистическая), частным случаем которой является корреляционная. Связь между двумя переменными x и y называется функциональной, если определенному значению переменной x строго соответствует одно или несколько значений другой переменной y, и с изменением значения x значение y меняется строго определенно. Такие связи обычно встречаются в точных науках. Например, известно, что площадь квадрата равна квадрату его стороны (S = a2). Это соотношение характерно для каждого единичного случая (квадрата), это так называемая жестко детерминированная связь. Такие связи можно встретить и в области экономических явлений. Например, при простой сдельной оплате труда связь между оплатой труда y и количеством изготовленных изделий xпри фиксированной расценке за одну деталь, например 5 руб., легко выразить формулой Существуют и иного рода связи, где взаимно действуют многие факторы, комбинация которых приводит к вариации значений результативного признака (показателя) при одинаковом значении факторного признака. Например, при изучении зависимости величины таможенных платежей, поступающих в федеральный бюджет, от количества товаров, перемещаемых через таможенную границу государства, (или от стоимостного товарооборота) последние будут рассматриваться как факторный признак, а величина таможенных платежей – как результативный. Между ними нет жестко детерминированной связи, т.е. при одном и том же количестве перемещенных через таможенную границу товаров (или стоимости товарооборота) величина таможенных платежей, перечисленных разными таможнями будет различной, так как кроме количества товаров, перемещаемых через таможенную границу государства, (или стоимость товарооборота) на величину таможенных платежей влияет много других факторов (различная номенклатура товаров, для которых применяются различные таможенные пошлины, сборы и льготы; различные таможенные режимы перемещения товаров через таможенную границу и др.), комбинация которых вызывает вариацию величины таможенных платежей. Там, где взаимодействует множество факторов, в том числе и случайных, выявить зависимости, рассматривая единичный случай, невозможно. Такие связи можно обнаружить только при массовом наблюдении как статистические закономерности39. Выявленная таким образом связь именуется стохастической40. Корреляционная связь41 – понятие более узкое, чем стохастическая связь, это ее частный случай. Именно корреляционные связи являются предметом изучения статистики. Корреляционная связь – это связь, проявляющаяся при большом числе наблюдений в виде определенной зависимости между средним значением результативного признака и признаками-факторами. Другими словами, корреляционную связь условно можно рассматривать как своего рода функциональную связь средней величины одного признака (результативного) со значением другого (или других). При этом, если рассматривается связь средней величины результативного показателя y с одним признаком-фактором x, корреляция называется парной, а если факторных признаков 2 и более (x1, x2, …, xm) – множественной42. По характеру изменений x и y в парной корреляции различают прямую и обратную связь. При прямой связи значения обоих признаков изменяются в одном направлении, т.е. с увеличением (уменьшением) значений x увеличиваются (уменьшаются) и значения y. При обратной связи значения факторного и результативного признаков изменяются в разных направлениях. Изучение корреляционных связей сводится в основном к решению следующих задач: выявление наличия (отсутствия) корреляционной связи между изучаемыми признаками; измерение тесноты связи между двумя (и более) признаками с помощью специальных коэффициентов (эта часть исследования именуется корреляционным анализом); определение уравнения регрессии – математической модели, в которой среднее значение результативного признака у рассматривается как функция одной или нескольких переменных – факторных признаков (эта часть исследования именуется регрессионным анализом). Общий термин «корреляционно-регрессионный анализ» подразумевает всестороннее исследование корреляционных связей (т.е. решение всех трех задач). Корреляционно-регрессионный анализ находит широкое применение в статистике. Рассмотрим его практическое применение на примере данных таможенной статистики внешней торговли России в 2006 году – таблица 39. Таблица 39. Величина внешнеторгового оборота и таможенных платежей
В качестве факторного признака x примем стоимостной внешнеторговый товарооборот в млрд. долл. США, а в качестве результативного признака y – величину таможенных платежей в федеральный бюджет в млрд. руб.
Для выявления наличия и характера корреляционной связи между двумя признаками в статистике используется ряд методов. 1. Рассмотрение параллельных данных(значений x и y в каждой из n единиц). Единицы наблюдения необходимо расположить по возрастанию значений факторного признака х (как в таблице справа) и затем сравнить с ним (визуально) поведение результативного признака у. В нашей задаче в 6 случаях по мере увеличения значений x увеличиваются и значения y, а в 5 случаях этого не происходит, поэтому затруднительно говорить о прямой связи между х и у. 2. Графический метод – это графическое изображение корреляционной зависимости. Для этого, имея n взаимосвязанных пар значений x и y и пользуясь прямоугольной системой координат, каждую такую пару изображают в виде точки на плоскости с координатами x и y. Совокупность полученных точек представляет собой корреляционное поле (рис. 20), а соединяя последовательно нанесенные точки отрезками, получают ломаную линию, именуемую эмпирической линией регрессии (рис. 21). 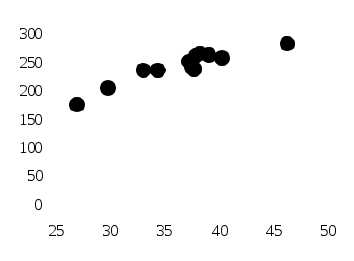 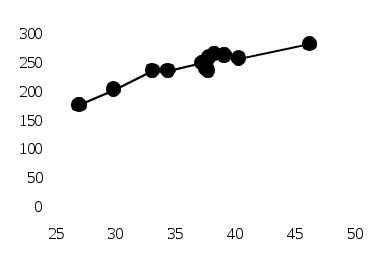 Рис. 20. Корреляционное поле Рис. 21. Эмпирическая линия регрессии Рис. 20. Корреляционное поле Рис. 21. Эмпирическая линия регрессииВизуально анализируя график, можно предположить характер зависимости между признаками x и y. В нашей задаче эмпирическая линия регрессии (рис.21) похожа на восходящую прямую, что позволяет выдвинуть гипотезу о наличии прямой зависимости между величиной стоимостного внешнеторгового товарооборота и величиной таможенных платежей в федеральный бюджет. 3. Метод аналитических группировокиспользуется при большом числе наблюдений для выявления корреляционной связи между двумя количественными признаками. Чтобы выявить наличие корреляционной связи между двумя признаками, проводится группировка единиц совокупности по факторному признаку х и для каждой выделенной группы рассчитывается среднее значение результативного признака Таблица 40. Условные пример аналитической группировки
В последнем столбце табл. 40 приведены средние величины, рассчитанные на основе индивидуальных данных об издержках отдельных предприятий каждой группы. Данные таблицы 40 свидетельствуют, что чем крупнее товарооборот, тем меньше издержки обращения. Таким образом, с помощью простой аналитической группировки можно выявить наличие зависимости между рассматриваемыми показателями: объемом товарооборота как показателем размера предприятий и средним уровнем издержек обращения. 4. Метод корреляционных таблиц предполагает комбинационное распределение единиц совокупности по двум количественным признакам. Такая таблица строится по типу «шахматной», т.е. в подлежащем (строках) таблицы выделяются группы по факторному признаку х, а в сказуемом (столбцах) – по результативному у (или наоборот), а в клетках таблицы на пересечении х и у показано число случаев совпадения каждого значения х с соответствующим значением у. Общий вид такой таблицы показан на условном распределении 40 единиц по признакам х и у, где х – стаж работы, у – производительность труда (число изделий, вырабатываемых в час одним рабочим) – таблица 41. Среднее значение по группам определяется по средней арифметической взвешенной по серединам группировочных интервалов. Таблица 41. Условные корреляционной таблицы
Как видно из таблицы 41, по мере увеличения значений х итоговые групповые средние На основе аналитических группировок и корреляционных таблиц можно не только выявить наличие зависимости между двумя коррелируемыми показателями, но и измерить тесноту этой связи, в частности, с помощью эмпирического корреляционного отношения.
k– число групп по результативному признаку у; Рассчитаем это отношение для нашего примера (таблица 41): Полученное значение 5. Коэффициент корреляции знаков (Фехнера) – простейший показатель тесноты связи, основанный на сравнении поведения отклонений индивидуальных значений каждого признака (x и y) от своей средней величины. При этом во внимание принимаются не величины отклонений ( Очевидно, что если знаки всех отклонений по каждому признаку совпадут, то КФ=1, что характеризует наличие прямой связи. Если все знаки не совпадут, то КФ=–1(обратная связь). Если же С=Н, то КФ=0. Итак, как и любой показатель тесноты связи, коэффициент Фехнера может принимать значения от 0 до Средние значения факторного и результативного признаков определяем по формуле средней арифметической простой (10): В двух последних столбцах таблицы 42 приведены знаки отклонений каждого х и у от своей средней величины. Число совпадений знаков – 10, а несовпадений – 2, тогда определяем коэффициент корреляции знаков (Фехнера) по формуле (121): КФ= Таблица 42. Вспомогательная таблица для расчета коэффициента Фехнера
Обычно такое значение показателя тесноты связи характеризует заметную прямую зависимость между x и y, однако, следует иметь в виду, что поскольку КФ зависит только от знаков и не учитывает величину самих отклонений х и у от их средних величин, то он практически характеризует не столько тесноту связи, сколько ее наличие и направление. 6. Линейный коэффициент корреляции – самый популярный измеритель тесноты линейной связи между двумя количественными признаками x и y. Он основан на предположении, что при полной независимости43 признаков x и у отклонения значений факторного признака от средней ( В отличие от КФ в линейном коэффициенте корреляции учитываются не только знаки отклонений от средних величин, но и значения самих отклонений, выраженные для сопоставимости в единицах среднего квадратического отклонения t: Линейный коэффициент корреляции r представляет собой среднюю величину из произведений нормированных отклонений для x и у: 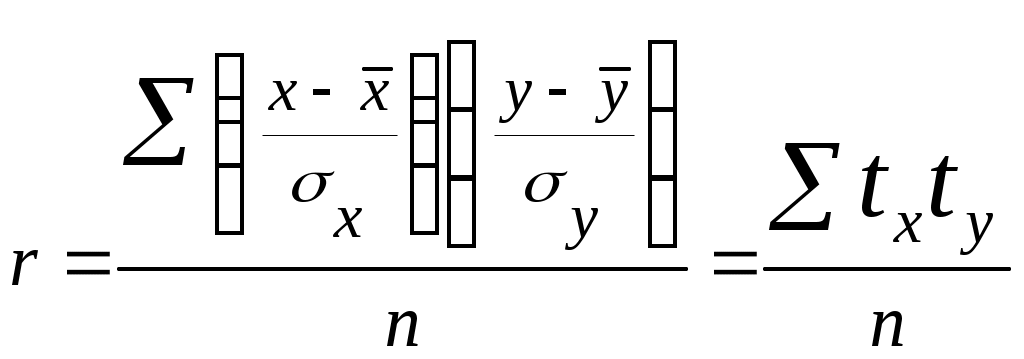 , (122) или , (122) или Числитель формулы (123), деленный на n, представляющий собой среднее произведение отклонений значений двух признаков от их средних значений, называется коэффициентом ковариации – это мера совместной вариации факторного x и результативного y признаков: Недостатком коэффициента ковариации является то, что он не нормирован, в отличие от линейного коэффициента корреляции. Очевидно, что линейный коэффициент корреляции представляет собой частное от деления ковариации между х и у на произведение их средних квадратических отклонений: Путем несложных математических преобразований44 можно получить и другие модификации формулы линейного коэффициента корреляции, например: 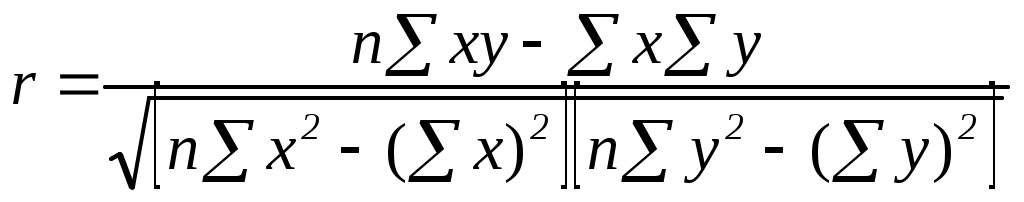 , (128) , (128) 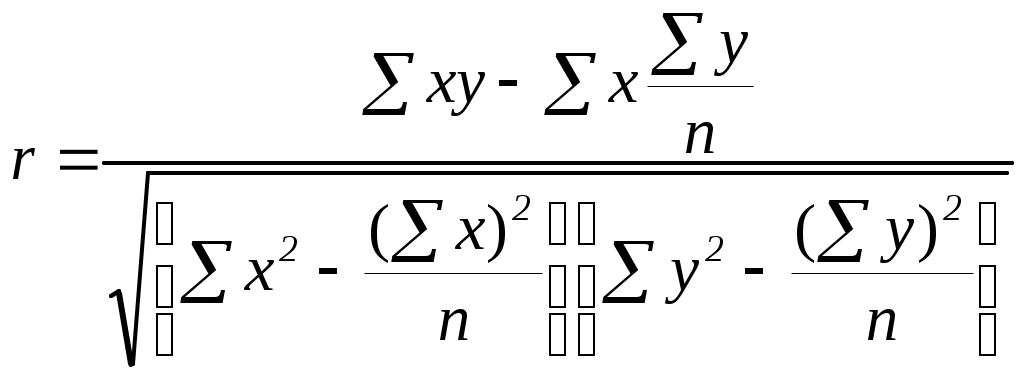 . (129) . (129)Линейный коэффициент корреляции может принимать значения от –1 до +1, причем знак определяется в ходе решения. Например, если Таблица 43. Шкала Чэддока
Таким образом, коэффициент корреляции при линейной зависимости служит как мерой тесноты связи, так и показателем, характеризующим степень приближения корреляционной зависимости между х и у к линейной. Поэтому близость значения r к 0 в одних случаях может означать отсутствие связи между х и у, а в других свидетельствовать о том, что зависимость не линейная. В нашей задаче для расчета rпостроим вспомогательную таблицу 44. Таблица 44. Вспомогательные расчеты линейного коэффициента корреляции
В нашей задаче: Тогда линейный коэффициент корреляции по формуле (122): r = 11,241/12 = 0,937. Аналогичный результат получаем по формуле (123): r = 1485,066/(12*4,784*27,618) = 0,937 Или по формуле (126): r = (106317,681/12 – 36,602*238,674) / (4,784*27,618) = 0,937, Найденное значение свидетельствует о том, что связь между величиной стоимостного внешнеторгового товарооборота и величиной таможенных платежей в федеральный бюджет очень близка к функциональной (сильная по шкале Чэддока). Проверка коэффициента корреляции на значимость (существенность). Интерпретируя значение коэффициента корреляции, следует иметь в виду, что он рассчитан для ограниченного числа наблюдений и подвержен случайным колебаниям, как и сами значения x и y, на основе которых он рассчитан. Другими словами, как любой выборочный показатель, он содержит случайную ошибку и не всегда однозначно отражает действительно реальную связь между изучаемыми показателями. Для того, чтобы оценить существенность (значимость) самого r и, соответственно, реальность измеряемой связи между х и у, необходимо рассчитать среднюю квадратическую ошибку коэффициента корреляции σr. Оценка существенности (значимости) r основана на сопоставлении значения r с его средней квадратической ошибкой: Существуют некоторые особенности расчета σr в зависимости от числа наблюдений (объема выборки) – n. Если число наблюдений достаточно велико (n>30), то σr рассчитывается по формуле (130): Обычно, если Если число наблюдений небольшое (n<30), то σr рассчитывается по формуле (131): а значимость r проверяется на основе t-критерия Стьюдента, для чего определяется расчетное значение критерия по формуле (132) и сопоставляется c tТАБЛ. Табличное значение tТАБЛ находится по таблице распределения t-критерия Стьюдента (см. Приложение 2) при уровне значимости α=1-β и числе степеней свободы ν=n–2. Если tРАСЧ> tТАБЛ ,то r считается значимым, а связь между х и у – реальной. В противном случае (tРАСЧ< tТАБЛ) считается, что связь между х и у отсутствует, и значение r, отличное от нуля, получено случайно. В нашей задаче число наблюдений небольшое, значит, оценивать существенность (значимость) линейного коэффициента корреляции будем по формулам (131) и (132): Из приложения 2 видно, что при числе степеней свободы ν = 12 – 2 = 10 (в 10-й строке) и вероятности β = 95% (уровень значимости α =1 – β = 0,05) tтабл=2,2281, а при вероятности 99% (α=0,01) tтабл=3,169, значит, tРАСЧ > tТАБЛ, что дает возможность считать линейный коэффициент корреляции r= 0,937 значимым. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

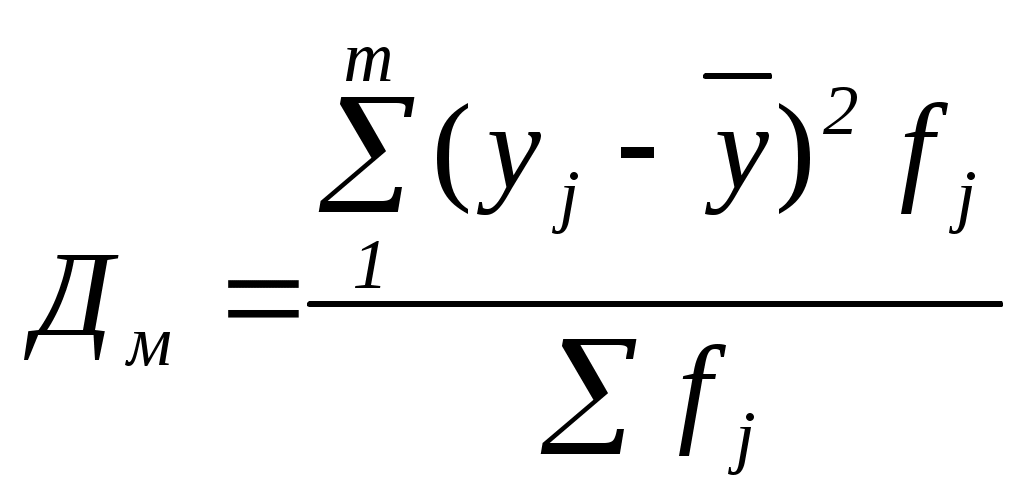 ,
,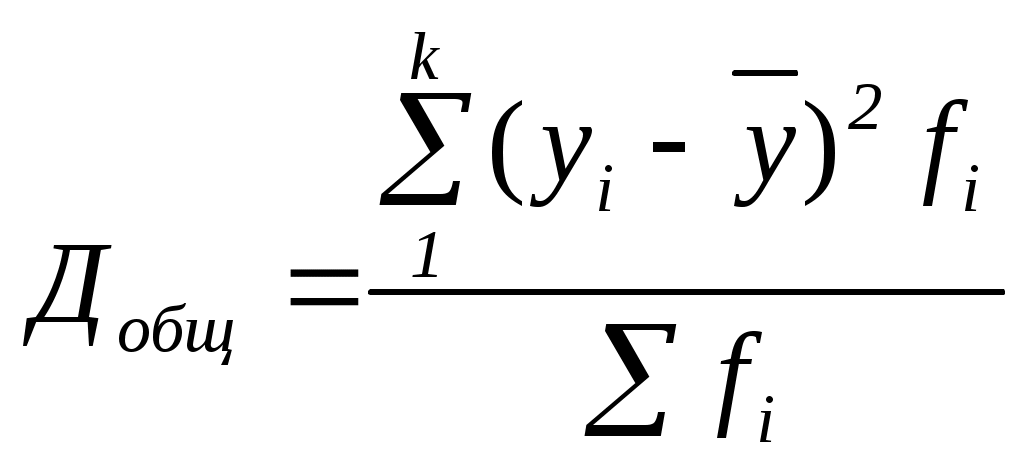 .
.