ответы на вопросы правовая статистика. 1. Предмет статистической науки. Теоритическая и методологическая основы статистики
 Скачать 351.59 Kb. Скачать 351.59 Kb.
|
|
В зависимости от содержания и познавательного значения наиболее часто выделяют следующие виды относительных величин: динамики, планового (нормативного) задания, выполнения планового (нормативного) задания, структуры, координации, интенсивности, сравнения и уровня экономического (социального) развития. Относительными величинами динамикиназываются статистические величины, характеризующие степень развития изучаемого явления во времени. Эти относительные величины называются также темпами роста. Относительные величины планового (нормативного) задания рассчитываются как отношение уровня показателя, запланированного (нормативного) на предстоящий (планируемый) период, к его уровню, достигнутому за предшествующий или базисный период. Относительные величины выполнения планового (нормативного) задания представляют собой отношение фактически достигнутого в отчетном периоде уровня показателя к запланированному (нормативному) заданию. Относительные величины динамики, планового (нормативного) задания и выполнения планового (нормативного) задания связаны между собой следующим соотношением: относительная величина динамики равна произведению относительных величин планового (нормативного) задания и выполнению планового (нормативного) задания. Если плановое задание предусматривает снижение уровня показателя, то результат сравнения фактического уровня с плановым заданием, т.е. относительная величина выполнения планового задания, меньше 1, или 100%, будет свидетельствовать о перевыполнении планового задания, а больше 1, или 100% - о недовыполнении планового задания. Относительные величины структуры 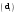 представляют собой соотношения размеров отдельных частей изучаемой совокупности (mi) и всей совокупности в целом представляют собой соотношения размеров отдельных частей изучаемой совокупности (mi) и всей совокупности в целом 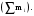
Относительные величины структуры характеризуют состав совокупности и показывают какую долю (или удельный вес) во всей совокупности составляют отдельные ее части. Изменение во времени (динамика) относительной величины структуры (удельного веса), а также части и целого, на основании которых рассчитан удельный вес, т.е. относительные величины второго порядка, связаны между собой следующим соотношением: относительная величина динамики, исчисленная для удельного веса, равна отношению относительной величины динамики части к относительной величине динамики целого. Относительные величины координациипредставляют собой соотношение отдельных частей целого между собой. При расчете относительных величин координации одну из составных частей целого принимают за базу, а затем находят отношение к ней всех остальных частей. Относительные величины интенсивностипредставляют собой показатели, характеризующие степень распространения или развития того или иного явления в определенной среде. Они рассчитываются путем сопоставления абсолютных величин, относящихся к различным совокупностям, но находящимся между собой в определенной связи. Характерным примером здесь являются демографические коэффициенты рождаемости, смертности, брачности, естественного прироста и др. Относительные величины сравнения представляют собой соотношения одноименных статистических величин, относящихся к разным объектам или разным территориям. Рассчитываются они, как правило, за один и тот же период времени, или на отдельный момент времени. Относительные величины уровня экономического (социального) развитияпредставляют собой статистические показатели, характеризующие размеры производства или потребления различных видов продукции, доходов и других показателей на душу населения. Например, производство электроэнергии на душу населения, потребление сахара на душу населения, денежные доходы на душу населения и др. 13. Виды средних степенных величин и методы их расчета. Средняя величина есть обобщенная количественная характеристика единиц совокупности по вариации определенного признака. Она рассчитывается на единицу этой совокупности. В статистике используются различные виды средних величин: агрегатная, арифметическая, гармоническая, геометрическая, средний квадрат и др. Выбор средней зависит как от поставленной задачи, которую правильно может разрешить только определенная средняя, так и от характера и содержания исходного материала, имеющегося в конкретном случае. При расчете средних величин необходимо исходить из экономического содержания статистических показателей. В основе такого подхода лежит исходное соотношение средней, а именно:
Так, например, средняя урожайность представляет собой соотношение сбора урожая со всей площади (валовой сбор) и размера посевной площади (выраженной в гектарах). Реализуя исходное выражение расчета средней, используются различные формулы расчета средних величин. Средняя арифметическая. Применяются формулы средней арифметической простой и взвешенной. Если исходные данные усредняемого признака представлены в не сгруппированном виде (как индивидуальные значения первичного признака у отдельных единиц совокупности), то в этом случае средняя рассчитывается по формуле средней арифметической простой:
где 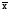 – среднее значение признака; х – индивидуальные значения признака у каждой единицы совокупности; – среднее значение признака; х – индивидуальные значения признака у каждой единицы совокупности; 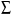 – знак суммирования; n – число единиц совокупности. – знак суммирования; n – число единиц совокупности.Если исходные данные представлены в сгруппированном виде, т.е. в виде рядов распределения (дискретных или интервальных), то средняя величина в таких случаях рассчитывается по формуле средней арифметической взвешенной:
где х – варианты значений осредняемого признака; f – частоты (веса) для каждого из вариантов признака, показывающие их повторяемость. Вычисление средней арифметической по вариационным интервальным рядам. В подобных рядах необходимо предварительно по каждой группе от интервальных значений признака перейти к их дискретным выражениям путем определения полусумм нижней и верхней границ интервалов ряда распределения. 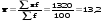 мин. мин.Структурные средние. К их числу относятся мода, медиана и соответствующие квартильные характеристики. Мода (М0) – величина признака (варианта), которая встречается в ряду распределения с наибольшей частотой (весом). В дискретных рядах распределения значение моды определяется визуально, то есть по наибольшей частоте. Если же варианты ряда распределения заданы в виде интервалов, равных по величине, то сначала находится модальный интервал, т.е. интервал, обладающий наибольшей частотой, а затем – приближенное значение модальной величины признака по формуле:
где xmo – нижняя граница модального интервала; imo – величина модального интервала; fmo-1 – частота интервала, предшествующего модальному; fmo – частота модального интервала; fmo+1 – частота интервала, следующего за модальным. Медиана (Ме) – величина признака у единицы совокупности, находящейся в середине ранжированного (упорядоченного) ряда. Если варианты в ряду распределения представлены в виде равных интервалов, то первоначально находят медианный интервал, который содержит единицу, находящуюся в середине ранжированного ряда. Для определения этого интервала сумму частот 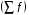 делят пополам и на основе последовательного накопления (суммирования) частот интервалов, начиная с первого, находят интервал, где расположена медианная единица. Приближенное значение медианы в медианном интервале исчисляют по формуле: делят пополам и на основе последовательного накопления (суммирования) частот интервалов, начиная с первого, находят интервал, где расположена медианная единица. Приближенное значение медианы в медианном интервале исчисляют по формуле:
где хme – нижняя граница медианного интервала; ime – величина медианного интервала; 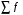 – сумма частот ряда; Sme-1 – накопленный итог численностей до медианного интервала; fme – численность медианного интервала. – сумма частот ряда; Sme-1 – накопленный итог численностей до медианного интервала; fme – численность медианного интервала.Вычислим значение медианной величины признака на основе данных табл.: 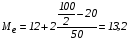 мин. мин.Следовательно, 50% изделий произведены с затратами времени 13,2 мин и меньше на одну деталь, а 50% – больше, чем 13,2 мин. 14. Ряды динамики, их виды и правила построения. Развитие общественных явлений во времени называется динамикой. Динамические ряды –это ряды статистических показателей, характеризующих развитие общественных явлений во времени Структура: Уровень ряда-Y Фактор времени -t Значение рядов динамики состоит в том, что они дают возможность выявить закономерности развития явлений, облегчают их анализа. Каждый ряд состоит из 2-х граф: в одной указываются периоды или даты времени, во второй – числовая характеристика изучаемого явления в эти периоды, называемая уровнем ряда. Уровни ряда могут выражаться абсолютными, средними и относительными величинами. Временные ряды, состоящие из абсолютных величин, могут быть двух видов: интервальные и моментные. В интервальном ряду приводятся данные, характеризующие состояние явления за определенный отрезок времени. Особенностью интервальных рядов динамики является то, что данные этих рядов можно суммировать и получать новые численные значения, относящиеся к более длительным периодам времени. Моментный ряд динамики состоит из показателей, характеризующих состояние явления на определенные моменты времени. Уровни моментных рядов складывать нельзя, так как слагающие явления единицы последовательно повторяются в различных уровнях ряда, поэтому их сумма не имеет смысла. К суммированию показателей интервального ряда часто прибегают для построения рядов динамики с нарастающими итогами. Если ряд динамики состоит из относительных или средних величин, то суммировать их нельзя, но разность их имеет реальный смысл. Для правильного построения рядов динамики необходимо соблюдать ряд требований: 1) Все показатели ряда динамики должны быть достоверными, точными, научно обоснованными. 2) Все показатели ряда должны быть сопоставимы. Основным условием сопоставимости статистических показателей является одинаковая методология их определения. 3) Показатели ряда динамики должны быть сопоставимы по территории, к которой они относятся. 4) Показатели ряда динамики должны быть сопоставимы во времени, т.е. они должны быть исчислены за одни и те же периоды времени или же на одну и ту же дату. 5) Все показатели ряда должны быть приведены в одних и тех же единицах измерения. При изучении рядов динамики статистика решает ряд задач: 1) измеряет абсолютную и относительную скорость роста либо снижения уровня за отдельные промежутки времени; 2) дает обобщающие характеристики уровня и скорости его изменения за тот или иной период; 3) выявляет и численно характеризует основные тенденции развития явления на отдельных этапах; 4) дает сравнительную числовую характеристику развития данного явления в разных регионах или на разных этапах; 5) выявляет факторы, обуславливающие изменение изучаемого явления во времени; 6) делает прогнозы развития явления в будущем. Для сравнения между собой отдельных уровней ряда динамики рассчитываются следующие показатели: абсолютные приросты, темпы роста (коэффициенты роста), темпы прироста и абсолютное значение одного процента прироста. Расчет этих показателей основан на сравнении между собой уровней ряда динамики. При этом уровень, с которым производится сравнение, может быть базисным или цепным. Абсолютный прирост показывает, насколько в абсолютном выражении уровень отчетного периода больше или меньше уровня базисного периода. Абсолютный прирост рассчитывается как с постоянной, так и переменной базой сравнения. Абсолютный прирост за единицу времени измеряет абсолютную скорость роста или снижения уровня. 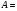 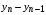 (переменная база сравнения); (переменная база сравнения);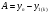 (постоянная база сравнения); (постоянная база сравнения);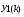 – уровень ряда, принятого за базу сравнения. – уровень ряда, принятого за базу сравнения.Коэффициент роста показывает, во сколько раз уровень отчетного периода больше или меньше уровня базисного и рассчитывается как с переменной, так и с постоянной базой сравнения. С переменной базой сравнения 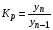 , с постоянной базой сравнения , с постоянной базой сравнения 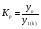 . Коэффициент роста может быть больше единицы, меньше единицы, равен единице. Коэффициенты роста, выраженные в процентах, носят название темпов роста. . Коэффициент роста может быть больше единицы, меньше единицы, равен единице. Коэффициенты роста, выраженные в процентах, носят название темпов роста.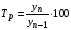 , ,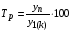 . .Ели коэффициенты роста, рассчитанные с переменной базой сравнения, характеризуют изменение явления от периода к периоду, то коэффициенты роста с постоянной базой – непрерывную линию развития. Темп прироста показывает, на сколько процентов уровень отчетного периода больше или меньше уровня базисного. При переменной базе сравнения: 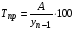 или или 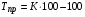 или или 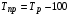 . .При постоянной базе сравнения: 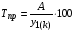 или или 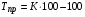 . .Между показателями динамики, вычисленными с постоянной и переменной базой, существует определенная связь. Так, сумма абсолютных приростов с переменной базой 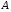 дает общий прирост за исследуемый период: дает общий прирост за исследуемый период: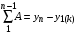 , ,где n – число уровней динамики ряда. При сопоставлении динамики развития двух явлений можно использовать показатель, предоставляющий собой отношение темпов роста за одинаковые отрезки времени по двум динамическим рядам. Этот показатель называют коэффициентом опережения. 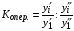  , ,где 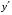 , , 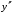 – соответствующие уровни сравниваемых динамических рядов. С помощью этого коэффициента могут сравниваться динамические ряды одинакового содержания, но относящиеся к разным территориям или к различным организациям или ряды разного содержания, характеризующие один и тот же объект. – соответствующие уровни сравниваемых динамических рядов. С помощью этого коэффициента могут сравниваться динамические ряды одинакового содержания, но относящиеся к разным территориям или к различным организациям или ряды разного содержания, характеризующие один и тот же объект.Для получения обобщающей характеристики интенсивности развития явления за длительный период исчисляют средние показатели динамики. Средний уровень ряда динамики исчисляется различно в зависимости от вида ряда. Для интервального ряда он рассчитывается по формуле средней арифметической простой: 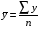 , ,где п – число уровней ряда. Для моментного ряда с равными интервалами по формуле средней хронологической простой: 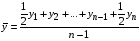 . .Для моментного ряда с неравными интервалами по формуле средней хронологической взвешенной: 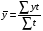 , ,где t – промежутки времени. Все остальные средние показатели для интервальных и моментных рядов динамики исчисляются одинаково. Средний абсолютный прирост ( 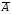 ) определяется по формуле средней арифметической из абсолютных приростов, исчисленных с переменной базой: ) определяется по формуле средней арифметической из абсолютных приростов, исчисленных с переменной базой: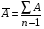 или или 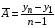 , ,где 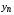 , , 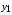 – конечный и начальный уровни динамического ряда. – конечный и начальный уровни динамического ряда.Средний коэффициент роста определяется по формуле средней геометрической из коэффициента роста за отдельные периоды: 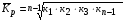 или или 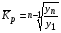 , ,где n – число уровней ряда. Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах: 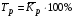 . .Средний темп прироста определяется, исходя из темпа роста: 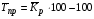 или или 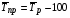 . .Выравнивание ряда по прямой предусматривает решение следующего уравнения: 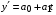 , где t – время (порядковый номер интервала или момент времени). , где t – время (порядковый номер интервала или момент времени).15. Аналитические показатели динамического ряда и способы их расчета Процессы и явления общественной жизни постоянно изменяются. Эти изменения изучаются в статистике с помощью построения рядов динамики, расчета системы аналитических и средних показателей, выявления основной тенденции (тренда) или сезонности развития общественных явлений. Рядами динамики называются ряды расположенных в хронологическом порядке показателей, характеризующих изменение размеров общественных явлений во времени. Ряд динамики состоит из двух основных элементов: во-первых, моментов или периодов времени (t), к которым относятся анализируемые данные; во-вторых, соответствующих им статистических показателей, которые называются уровнями динамического ряда (y). При изучении динамики общественных явлений рассчитывают следующую систему аналитических показателей: абсолютные приросты, темпы роста, темпы прироста и абсолютное значение (содержание) одного процента прироста либо снижения. Расчет этих показателей основан на абсолютном или относительном сравнении уровней динамического ряда. При этом, если каждый уровень сравнивается с его предыдущим уровнем, получают цепные показатели, а если каждый уровень сравнивается с начальным или каким-либо другим, принятым за постоянную базу сравнения (например, уровень, с которого начинается какой-либо новый этап развития явления), то получают базисные показатели динамики. Абсолютный прирост – это разность двух уровней ряда динамики. Он показывает, на сколько абсолютных единиц данный уровень больше или меньше уровня, взятого для сравнения, и выражается в тех же единицах измерения, что и уровни анализируемого ряда. Цепной абсолютный прирост( 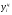 ) исчисляется как разность между сравниваемым уровнем ( ) исчисляется как разность между сравниваемым уровнем (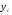 ) и предшествующим ему уровнем ( ) и предшествующим ему уровнем (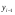 ): ):
Базисный абсолютный прирост ( 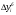 ) исчисляется как разность между сравниваемым уровнем и уровнем, принятым за постоянную базу сравнения (y0): ) исчисляется как разность между сравниваемым уровнем и уровнем, принятым за постоянную базу сравнения (y0):
Абсолютный прирост может иметь положительный или отрицательный знак, в последнем случае это не прирост, а снижение. Сумма цепных абсолютных приростов за определенный период времени равна базисному абсолютному приросту за весь этот период. А разность между анализируемым и предыдущим базисными абсолютными приростами дает соответствующий цепной абсолютный прирост. Темп роста – это отношение двух уровней ряда динамики. Он выражается в коэффициентах или в процентах. В первом случае он показывает, во сколько раз данный уровень больше или меньше уровня, взятого для сравнения, во втором – сколько процентов данный уровень составляет по отношению к другому уровню, взятому для сравнения. Цепной темп роста ( 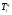 ) исчисляется как отношение между сравниваемым уровнем и предшествующим ему уровнем: ) исчисляется как отношение между сравниваемым уровнем и предшествующим ему уровнем:
Базисный темп роста ( 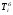 ) исчисляется как отношение между сравниваемым уровнем и уровнем, принятым за постоянную базу сравнения: ) исчисляется как отношение между сравниваемым уровнем и уровнем, принятым за постоянную базу сравнения:
Если темп роста меньше единицы, то имеет место не рост, а снижение (падение) анализируемого уровня. Последовательное произведение цепных темпов роста за определенный период времени, выраженных в коэффициентах, дает базисный темп роста за этот же период. А отношение анализируемого базисного темпа роста к предыдущему дает соответствующий цепной темп роста. Темп прироста – это отношение абсолютного прироста к уровню, принятому за базу сравнения. Он обычно выражается в процентах и показывает, на сколько процентов уровень данного периода больше (или меньше) базисного. Цепной темп прироста ( 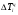 ) равен: ) равен:
Базисный темп прироста ( 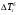 ) равен: ) равен:
Темп прироста вычисляется и как разность между темпом роста, выраженным в процентах, и 100%:
Темп прироста может иметь как положительный, так и отрицательный знак. Следовательно, количественно абсолютное значение одного процента равно одной сотой части уровня, предшествующего анализируемому, и выражается в тех же единицах, что и соответствующие уровни. При анализе и сопоставлении рядов динамики, характеризующих социально-экономические явления, рассчитывают коэффициенты опережения. Они представляют собой отношение темпов роста или прироста за одинаковые отрезки времени по двум динамическим рядам:
где Т'р, Т''р, Т'рп, Т''пр – соответственно темпы роста и темпы прироста сравниваемых динамических рядов. Уровни и аналитические показатели динамики изменяются во времени. Поэтому для обобщающей характеристики всего ряда динамики в целом используются средние величины: средний уровень, средний абсолютный прирост, средний темп роста и прироста. Средний уровень ряда динамики характеризует типичную величину абсолютных уровней. Он называется также средней хронологической, или временной средней и рассчитывается для разных рядов динамики по-разному. В интервальных рядах с равными отрезками времени применяется средняя арифметическая простая:
где n – число уровней ряда. В интервальных рядах с неравными отрезками времени используетсясредняя арифметическая взвешенная: В моментных рядах с равными промежутками между датами средний уровень рассчитывается по формуле:
где n -число дат, (n-1) - число равных промежутков времени. В моментных рядах с неравными промежутками между датами средний уровень рассчитывается двумя способами в зависимости от характера исходных данных. Если известны данные на начало изучаемого периода, а также изменения уровней ряда, то средний уровень рассчитывается по средней арифметической взвешенной:
где ti - продолжительность i-го отрезка времени. Если имеются данные на начало и конец периода, а также значения уровней динамического ряда на отдельные моменты времени внутри изучаемого периода, то средний уровень ряда рассчитывается по следующей формуле:
где 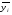 – промежуточная средняя, равная – промежуточная средняя, равная 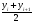 , ,ti - продолжительность промежутка времени между соответствующими датами. Средний абсолютный прирост (или средняя абсолютная скорость роста) показывает, на сколько единиц в среднем увеличивался или уменьшался уровень динамического ряда за соответствующий период времени (за месяц, за квартал и т.д.) Он рассчитывается по средней арифметической простой из цепных абсолютных приростов за последовательные и равные по продолжительности периоды:
где n – число цепных абсолютных приростов. Средний темп роста рассчитывается по средней геометрической из цепных темпов роста, выраженных в коэффициентах: а) с равными отрезками времени
где n – число цепных темпов роста; б) с неравными отрезками времени:
где ti - продолжительность соответствующих отрезков времени. Средний темп прироста показывает, на сколько процентов в среднем за единицу времени увеличивался или уменьшался уровень ряда динамики. Он рассчитывается как разность между средним темпом роста ( 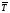 ) и 100%, если ) и 100%, если 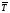 выражен в процентах, а если выражен в процентах, а если 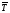 выражен в коэффициентах, то выражен в коэффициентах, то 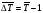 . .16. Средние показатели динамического ряда и способы их расчета. Уровни и аналитические показатели динамики изменяются во времени. Поэтому для обобщающей характеристики всего ряда динамики в целом используются средние величины: средний уровень, средний абсолютный прирост, средний темп роста и прироста. Средний уровень ряда динамики характеризует типичную величину абсолютных уровней. Он называется также средней хронологической, или временной средней и рассчитывается для разных рядов динамики по-разному. В интервальных рядах с равными отрезками времени применяется средняя арифметическая простая:
где n – число уровней ряда. В интервальных рядах с неравными отрезками времени используется средняя арифметическая взвешенная: В моментных рядах с равными промежутками между датами средний уровень рассчитывается по формуле:
где n -число дат, (n-1) - число равных промежутков времени. В моментных рядах с неравными промежутками между датами средний уровень рассчитывается двумя способами в зависимости от характера исходных данных. Если известны данные на начало изучаемого периода, а также изменения уровней ряда, то средний уровень рассчитывается по средней арифметической взвешенной:
где ti - продолжительность i-го отрезка времени. Задача. В январе в списочном составе работников предприятия произошли следующие изменения, чел.: состояло по списку на 1.01. 540 выбыло с 8.01 5 зачислено с 14.01 4 зачислено с 25.01 3 Необходимо определить среднедневную численность работников предприятия за январь. Решение. Для определения среднедневной численности работников рассчитаем продолжительность (t) каждого календарного периода с постоянной численностью работающих и общее число человеко-дней:
Таким образом, среднесписочная численность работников в январе составит: 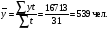 Если имеются данные на начало и конец периода, а также значения уровней динамического ряда на отдельные моменты времени внутри изучаемого периода, то средний уровень ряда рассчитывается по следующей формуле:
где 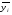 – промежуточная средняя, равная – промежуточная средняя, равная 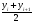 , ,ti - продолжительность промежутка времени между соответствующими датами. Средний абсолютный прирост (или средняя абсолютная скорость роста) показывает, на сколько единиц в среднем увеличивался или уменьшался уровень динамического ряда за соответствующий период времени (за месяц, за квартал и т.д.) Он рассчитывается по средней арифметической простой из цепных абсолютных приростов за последовательные и равные по продолжительности периоды:
где n – число цепных абсолютных приростов. Средний темп роста рассчитывается по средней геометрической из цепных темпов роста, выраженных в коэффициентах: а) с равными отрезками времени
где n – число цепных темпов роста; б) с неравными отрезками времени:
где ti - продолжительность соответствующих отрезков времени. Средний темп прироста показывает, на сколько процентов в среднем за единицу времени увеличивался или уменьшался уровень ряда динамики. Он рассчитывается как разность между средним темпом роста ( 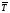 ) и 100%, если ) и 100%, если 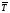 выражен в процентах, а если выражен в процентах, а если 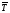 выражен в коэффициентах, то выражен в коэффициентах, то 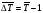 . .17. Понятие об экстраполяции уровней динамических рядов. Экстраполяция динамического ряда – нахождение неизвестного уровня за пределами динамического ряда. Вида экстраполяции: - ретроспективная экстраполяция – нахождение неизвестного уровня к прошлому. - перспективная экстраполяция – прогноз в сторону будущего. Правило: Если явление (показатель) в динамике развивается по законам арифметической прогрессии, тогда применяется следующая формула: Уt = Уо (+/-) t Уt – искомый уровень ряда; Уо – базисный уровень ближайших к искомому; t – период времени между Уо и Уt Если прогноз, то значение +, если интерполяция (нахождение неизвестного уровня внутри динамического ряда), то значение «-». Правило: Если показатель развивается по геометрической прогрессии, то используется следующая формула: Уt = Уо (х/:) Тt х-прогнозирование; : -интерполяция. Пример: Численность населения области на начало 2017 года составляло 1370 тыс.чел., в том числе городское население 850 тыс.чел. Городское население увеличивалось за последние 20 лет в среднем за год на 2,2 %, а сельское население уменьшалось на 0,5 %. Определить возможную численность всего населения области к концу 2022 года, при условии сохранения прежних тенденций. Уо = 1370; Уо (гор.) = 850; Уо (сел.) = 520. Тt (гор.) = 102,2 %, Тt (сел.) = 99,5 %. Применяем формулу: Уt = Уо х Тt. У (гор.) 2022 г. = 850х 1,022 (в 6 степени) = 968 тыс. У (сел.) 2022 г. = 520х 0,995 (в 6 степени) = 505 тыс. Итого: 1473 тыс.чел. Т(тем роста) = 1473:1370=1,075=7,5%. |

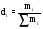
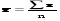 ,
,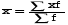 ,
,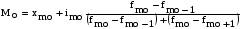
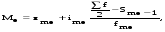
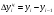 .
.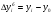 .
. 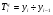 .
.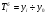
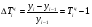
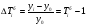
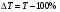
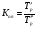 ;
;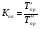 ,
,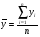 ,
,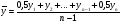
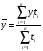 ,
,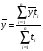
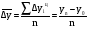 ,
,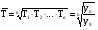 ,
,