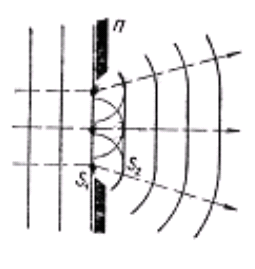
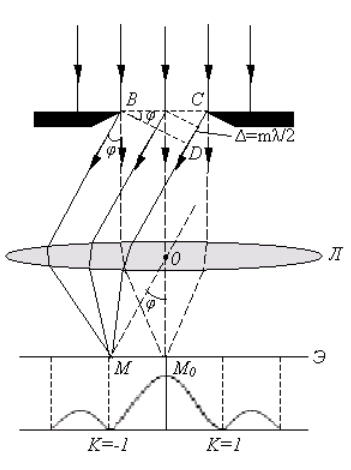
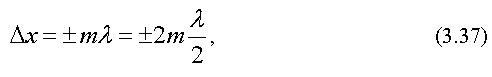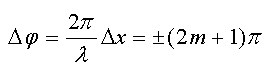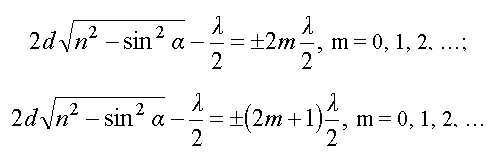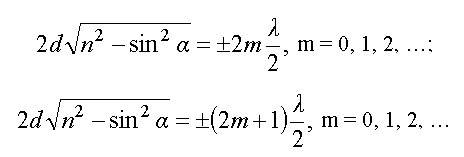Шпора к экзамену 2 курс 2сем.. 1, Система уравнений Максвела в интегральной форме
 Скачать 1.11 Mb. Скачать 1.11 Mb.
|
|
- - 1, Система уравнений Максвела в интегральной формеСогласно Максвелу переменные электрические и магнитные поля взаимосвязаны(одно переменное поле порождает другое) и удовлетворяют следующей системе уравнений. Эти уравнения дополняются выражением для силы Лоренца, описывающей движение свободных зарядов в электрических и магнитных полях F=qE+q[v,B]. (2) Если поля стационарны (Е=const и В=const), то уравнения (1) принимают вид Из этих уравнений следует, что стационарные электрические и магнитные поля в отличие от переменных полей могут существовать раздельно. Уравнения Максвела являются постулатами(аксиомами) современной теории электромагнетизма. Их нельзя доказать. Можно указать лишь логическиe посылки, приводящие к этим уравнениям. Систему уравнений Максвела можно дополнить граничными условиями, для векторов В, E, H, D, которые для границы раздела двух сред, на которой нет свободных зарядов и токов проводимости, имеют вид D1n=D2n, E1=E1, (4) B1n=B2n, H1=H1, где индекс n означает нормальную составляющую поля, а - тангенциальную или касательную к границе раздела. Уравнения Максвела не содержат никаких предположений о свойствах среды, в которой существует электромагнитное поле. Свойства среды учитываются с помощью уравнений, которые называют материальными D=0E, B=0j=E, (5) где и - электрическая и магнитная проницаемости среды, и -электрическая и магнитная постоянные, - проводимость среды. Обоснование различных представлений для , и выходит за рамки теории Максвела, так как требует предположений о свойствах вещества. Система уравнений Максвела в дифференциальной формеПереход к дифференциальной форме осуществляется с помощью теоремы Остроградского-Гаусcа и теоремы Стокса гдепроизвольный вектор, а (дельта) – дифференциальный оператор равный Используя эти теоремы, получим Из последних частей этих равенств получим Это уравнения Максвела в дифференциальной Форме. Если среда диэлектрическая или вакуум (в такой среде нет свободных зарядов = 0 и токов проводимостиj = 0) , то система уравнений (5) принимает вид (6) ---------2------Волновые процессыВолной называется процесс распространения колебаний или других возмущений в пространстве. Основными видами волн являются механические упругие волны, волны на поверхности жидкости и электромагнитные волны. Упругими волнами называются волны, которые могут распространяться в упругой среде (т. е. среде, которая сопротивляется сжатию: твердой, жидкой и газообразной). К ним относятся, в частности, ударные, звуковые и сейсмические волны. Упругие волны называют также механическими волнами. Электромагнитные волны могут распространяться как в среде, так и в вакууме (например, радиоволны, световые волны). Характерным свойством волн является перенос энергии без переноса вещества. Например, по некошенному полю пшеницы от порывов ветра распространяется волна. При этом колосья колеблются около своих положений равновесия, а волна идет по всему полю. Рассмотрим этот процесс более подробно. Частицы среды, в которой распространяется волна, колеблются около своих положений равновесия. В зависимости от направления колебаний частиц среды по отношению к направлению распространения волны различают волны продольные и поперечные. В продольной волне частицы колеблются вдоль направления распространения волны, в поперечной волне колебания частиц совершаются перпендикулярно направлению распространения волны. В жидкой и газообразной среде возможно распространение только продольных волн, в твердой среде - как продольных, так и поперечных. .2.2. Характеристики волнового процессаПоскольку волна - это процесс распространения колебаний в пространстве, то для волнового процесса используются те же характеристики, что и для колебаний (T , ν ,φ ,ω ,A ), но вводятся еще и новые характеристики. Такими характеристиками являются: скорость волны - v, длина волны - λ, волновое число - k. При волновых процессах вводятся такие понятия, как фронт волны и волновая поверхность. Фронтом волны называется поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. Волновой поверхностью называется геометрическое место точек, колеблющихся в одинаковой фазе. Волновых поверхностей существует бесчисленное множество, в то время как фронт волны один. Простейшие волновые поверхности - плоскости и сферы. Если волновые поверхности представляют собой плоскости, то волна называется плоской, если они представляют собой множество концентрических сфер, то это сферическая волна. На больших расстояниях от точечного источника можно небольшие участки волновой поверхности считать плоскими. Скоростью волны v называется скорость перемещения волновой поверхности (фазовая скорость). Экспериментально ее можно найти, определив скорость перемещения фронта волны. Длиной волны λ называется расстояние, пройденное волновой поверхностью за период колебаний. Длина волны вычисляется по формуле Связь длины волны и частоты дается формулой Волновым числом называется величина  Электромагнитные волныЭлектромагнитными волнами называется процесс распространения в пространстве переменного электромагнитного поля. Теоретически существование электромагнитных волн предсказано английским ученым Максвеллом в 1865 г., а впервые они экспериментально получены немецким ученым Герцем в 1888 г. Из теории Максвелла вытекают формулы, описывающие колебания векторов и . Плоская монохроматическая электромагнитная волна, распространяющаяся вдоль оси x, описывается уравнениями 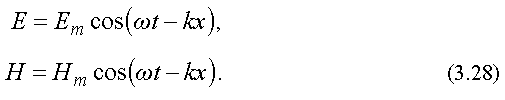 Здесь E и H - мгновенные значения, а Em и Hm - амплитудные значения напряженности электрического и магнитного полей, ω - круговая частота, k - волновое число. Векторы и колеблются с одинаковой частотой и фазой, взаимно перпендикулярны и, кроме того, перпендикулярны вектору - скорости распространения волны (рис. 3.7). Т. е. электромагнитные волны поперечны. В вакууме электромагнитные волны распространяются со скоростью . В среде с диэлектрической проницаемостью ε и магнитной проницаемостью µ скорость распространения электромагнитной волны равна: 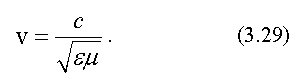 Частота электромагнитных колебаний, так же, как и длина волны, могут быть в принципе любыми. Классификация волн по частоте (или длине волны) называется шкалой электромагнитных волн. Электромагнитные волны делятся на несколько видов. Радиоволны имеют длину волны от 103 до 10-4 м. Световые волны включают:
Рентгеновское излучение - . Гамма-излучение имеет длину волны < 10-12 м. 3, Волновое уравнениеЕсли среда диэлектрическая или вакуум (в такой среде нет свободных зарядов = 0 и токов проводимостиj = 0) , то система уравнений Максвелла принимает вид Запишем уравнения (6) через векторыE иB. С учетомD=E иB=H получим Умножим обе части левых уравнений (1) векторно на оператор . Получим преобразуем векторные произведения в формулах (2) (3) где учтено, что согласно (1) E=0 и введен оператор (дельта) С учетом (3) уравнения (2) можно записать в виде где Величина называется электродинамической постоянной. Она совпадает со скоростью света в вакууме. Уравнение вида называется волновым уравнением. Параметр v в этом уравнении есть скорость распространения волны. Функция f=f(x,y,z,t), входящая в волновое уравнение, называется уравнением волны или волновой Функцией. Согласно волновым уравнениям (5) возможно существование электрической и магнитной волн в свободном пространстве с диэлектрической и магнитной проницаемостями и , и в частности в вакууме, где и . Однако поля Е иВ в этих волнах не являются независимыми, а связаны уравнениями Максвела, поэтому в природе существуют только электромагнитные волны, в которых изменяющееся эл. полеE порождает изменяющееся во времени магнитное полеB, и наоборот. Можно показать, что ЭМ-волны являются поперечными, т.е. векторыЕ иB в ЭМ-волне перпендикулярны направлению распространения волны. ------------4---------- Фазовая и групповая скорость частиц Излучение в некоторых условиях проявляет корпускулярные свойства. С другой стороны, дифракционная картина, наблюдаемая при рассеянии на кристаллах различных частиц — электронов, нейтронов и целых атомов — свидетельствует в пользу их волновой природы. Как совместить волновые и корпускулярные свойства объектов микромира? Ведь частица локализована в пространстве, а волна представляет собой протяжённое образование. Например, монохроматическая волна заполняет собой всё пространство и вопрос о её местонахождении лишён смысла. Тем не менее, волновой процесс можно локализовать. Для этого надо создать волновой пакет — сумму многих колебаний с разными частотами и длинами волн. Фазовая скорость Запишем уравнение монохроматической волны, распространяющейся в положительном направлении оси x: (x,t) = A cos(kx– t), где — любая физическая величина, описывающая волновое движение. Аргумент гармонической функции (в данном случае — косинуса) называется фазой: = kx – t. Выразим координату через фазу и время: Если мы зафиксируем фазу, то координата становится линейной функцией времени. Такая зависимость называется характеристикой. На рисунке 6.1.1 показаны три характеристики, 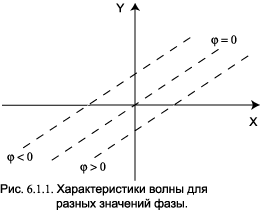 отвечающие различным значениям фазы. Множитель перед t называется фазовой скоростью волны: Физический смысл фазовой скорости заключается в следующем. Для наблюдателя, который движется со скоростью Vф в направлении распространения волны, величина становится постоянной и волна как бы застывает. Однако, во многих случаях оказывается, что фазовая скорость волны больше скорости света. Здесь нет никаких противоречий, так как темп переноса энергии описывается совсем другой характеристикой волнового пакета. Групповая скорость Понятие групповой скорости связано с интерференцией колебаний, имеющих разные частоты и длины волн. Рассмотрим две волны с одинаковыми амплитудами и различающимися, но близкими частотами и длинами волн: причём Сложим эти колебания: В аргументе первого косинуса правой части мы пренебрегли слагаемыми Δω и k по сравнению с 2 и 2k. На рис.6.2.1 приведён график функции (x) в некоторый момент времени. Результирующее колебание представляет собой волну практически с прежними значениями частоты и волнового числа, но с модулированной амплитудой. Мы можем добиться того, чтобы для нас стала неподвижной картина модуляции амплитуды. Для этого надо двигаться со скоростью (2.1) До сих пор мы рассматривали одномерный случай. На рис.6.2.2 представлена имитация сложения волн, распространяющихся в разных направлениях на плоскости. Из равноотстоящих точек под разными углами проведено по пять линий. Хорошо видно, как они образуют периодические сгущения и разрежения по обоим направлениям. Если сложить большое число волн, то получится более сложная картина биений с большей степенью локализации колебаний, но элементы периодической структуру будут многократно повторяться. Этот результат пока ещё отличается от наших представлений о частице, находящейся в определённой области пространства. Локализацию волнового пакета можно получить только при непрерывном распределении частот и волновых чисел. Тогда частоту можно представить как непрерывную функцию волнового вектора: (2.2) = (k). Зависимость (2.2) называется дисперсионным уравнением. Именно для такой функции вводится понятие групповой скорости как предела (2.1): Групповая скорость есть скорость передачи любого сигнала, а также скорость переноса энергии, массы и аналогичных величин. Она никогда не превосходит скорости света в вакууме. 5 Корпускулярно-волновой дуализм - это свойство материальных объектов, заключающееся в том, что в поведении данного объекта могут проявляться и волновые и корпускулярные свойства. До конца XIX в. считалось, что излучение имеет чисто волновую природу. Правда, гипотеза о корпускулярном строении света высказывалась ранее неоднократно. Её разделял, например, Ньютон. Однако, после исследований Френеля и Юнга в начале XIX в. по интерференции и дифракции световых волн и, особенно, после создания Максвеллом электродинамики во второй половине XIX в. возобладала волновая концепция. Но на рубеже XIX и XX вв. появились факты, свидетельствующие в пользу квантовой природы излучения. В 1900 г. Планк в основу теории чёрного тела положил гипотезу о квантованных осцилляторах. Он предположил, что стенки полости обмениваются энергией с полем излучения, причём порции энергии не могут быть меньше, чем ħω, где ω — собственная частота осциллятора. Позднее, в 1905 г. Эйнштейн предложил объяснение фотоэффекта, в котором квантовые свойства имеет уже само излучение, а не только гипотетические осцилляторы полости. Электромагнитное излучение характеризуется волновым вектором k и частотой ω. Описание плоской волны с точки зрения волновой теории имеет вид: где ψ— любая величина, принимающая участие в волновом движении, а ψ0 — её амплитуда. Попытаемся теперь перейти к квантовому описанию волнового процесса, то есть, напишем формулу, в которой будут присутствовать как волновые, так и корпускулярные характеристики объекта. По Планку и Эйнштейну энергия кванта связана с частотой волны: а его импульс — с её волновым вектором: В результате корпускулярная интерпретация формулы (1) выглядит следующим образом: Это уравнение выражает корпускулярно-волновой дуализм: описание волны в качестве параметров содержит энергию и импульс частицы. 6, Интерференция - это перераспределение потока электромагнитной энергии в пространстве, возникающее в результате наложения волн, приходящих в данную область пространства от разных источников. Если в области интерференции световых волн поставить экран, то на нем будут наблюдаться светлые и темные области, например полосы. И  нтерферировать могут только когерентные волны. Источники(волны) называют когерентными, если они имеют одинаковую частоту и постоянную во времени разность фаз, излучаемых ими волн. нтерферировать могут только когерентные волны. Источники(волны) называют когерентными, если они имеют одинаковую частоту и постоянную во времени разность фаз, излучаемых ими волн.Количественное описание интерференции волн.  Пусть две волны, приходят в точку О от источников S1 и S2 по разным оптическим путям L1=n1l1 и L2=n2l2. Напряженность результирующего поля в точке наблюдения равна E=E1+E2. (1) Детектор излучения(глаз) регистрирует не амплитуду, а интенсивность волны, поэтому возведем соотношение (1) в квадрат и перейдем к интенсивностям волн E2=E12+E22+E1E2 (2) Усредним это выражение по времени Последнее слагаемое в (3) 2 2<E1E2>=2 где - угол между векторами E1 и E2 . Если /2 , тo cos=0 и интерференционный член будет равен нулю. Это означает, что волны, поляризованные в двух взаимно перпендикулярных плоскостях интерферировать не могут. Если вторичные источники, от которых наблюдают интерференцию, получены от одного первичного источника, то векторыE1 иE2 параллельны и cos=1. В этом случае (3) можно записать в виде где усредняемые по времени функции имеют вид E1=E10cos(t+), E2=E20cos(t+), (6) =-k1l1+1, =-k2l2+2. Вычислим в начале среднее по времени значение интерференционного члена  (7) (7)откуда при =: Обозначая I1=E210, I2=E220 и I=I1+I2, (9) а если когерентны, то I=I1+I2+2 где k2l2-k1l1+- (11) есть разность фаз складываемых волн. Для источников. полученных от одного первичного источника 1=2 , поэтому =k2l2-k1l1=k0(n2l2-n1l1)=(2/) (12) где К0=2 - волновое число в вакууме, - оптическая разность хода лучей 1 и 2 от S1 и S2 до точки наблюдения интерференции 0. Получили Из формулы (10) следует, что в точке 0 будет максимум интерференции, если cos = 1, откуда m, или =m (m=0,1,2,…) (14) Условие минимума интерференции будет при cos = -1, откуда =2(m+½), или =(m+½) (m=0,1,2,…) (14) Таким образом, волны в точке наложения усилят друг друга, если их оптическая разность хода равна четному числу полуволн ослабят друг друга если она равна нечетному числу полуволн. Опыт Юнга (деление волнового фронта) П  ервый опыт по наблюдению интерференции был осуществлен Юнгом (1802). Излучение от точечного источника S проходило через два точечных отверстия S1 и S2 в диафрагме D и в точке Р на экране Э наблюдалась интерференция лучей 1 и 2, проходящим по геометрическим путям SS1P и SS2P. Рассчитаем интерференционную картину на экране. Геометрическая разность хода лучей 1 и 2 от источника S до точки Р на экране равна l=(l`2+l2) (l`1+l1)= (l`21`1)+(l2l1) (1) Пусть d – расстояние между S1 и S2, b – расстояние от плоскости источника S до диафрагмы Д, a – расстояние от диафрагмы Д до экрана Э, x – координата точки P на экране отностительно его центра, а x` - координата источника S относительно центра плоскости источника. Тогда согласно рисунку по теореме Пифагора получим Аналогичными будут выражения для l`1 и l`2, если заменить ab, xx`. Предположим, что d и x<  (3) (3)Аналогично С учетом (3) и (4) геометрическая разность хода лучей 1 и 2 будет равна Если лучи 1 и 2 проходят в среде с показателем преломления n, то их оптическая разность хода равна Условия максимумов и минимумов интерференции на экране имеют вид  (7) (7)Откуда координаты максимумов х=хm и минимумов х=х'm интерференционной картины на экране Если источник имеет вид полоски с координатой x', перпендикулярной плоскости рисунка, то изображение на экране также будет иметь вид полосок с координатой х , перпендикулярных плоскости рисунка. Расстояние между ближайшими максимумами и минимумами интерференции или ширина интерференционных полос (темных или светлых) будет согласно (8) равна x=xm+1-xm=x`m+1-x`m= где =/n – длина волны в среде с показателем преломления n. Принципы Гюйгенса и Гюйгенса-Френеля. В  волновой оптике существует два принципа: принцип Гюйгенса и принцип Гюйгенса-Френеля. В принципе Гюйгенса постулируется, что каждая точка фронта волны является источником вторичных волн. Построив огибающую этих волн, можно найти положение фронта волны в последующие моменты времени. Принцип Гюйгенса является чисто геометрическим и позволяет вывеcти. например, законы отражения и преломления света, объясняет явления распространения света в анизотропных кристаллах(двойное лучепреломление). Но он не может объяснить большинство оптических явлений, обусловленных интерференцией волн. Френель дополнил принцип Гюйгенса условием интерференции вторичных волн, исходящих от фронта волны. Такое расширение принципа Гюйгенса получило название принципа Гюйгенса-Френеля. 7, . Условия максимума и минимума интенсивности |