Шпора к экзамену 2 курс 2сем.. 1, Система уравнений Максвела в интегральной форме

• Название: 1, Система уравнений Максвела в интегральной форме
• Анкор: Шпора к экзамену 2 курс 2сем..doc
• Дата: 16.12.2017
• Размер: 1.11 Mb.
• Имя файла: Шпора к экзамену 2 курс 2сем..doc
• Тип: Документы; #11678
• Категория: Физика
• страница: 8 из 10

Уравнение Шредингера

Уравнение Шредингера лежит в основе квантовой механики. Оно, как и уравнение Ньютона, не выводится, а является обобщением опытных фактов. Его справедливость доказывается совпадением результатов, полученных из его решения и экспериментов. Уравнение Шредингера для стационарных состояний, т. е. для состояний с фиксированными значениями энергии, имеет вид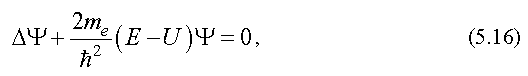



где 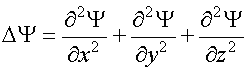   - сумма вторых частных производных от волновой функции по координатам;
      m_e  - масса частицы;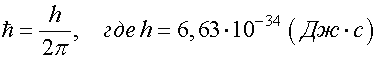
          - постоянная Планка;
     E - полная энергия частицы;
     U - потенциальная энергия частицы.

Из решения уравнения Шредингера для конкретного случая находят вид волновой функции Ψ, квадрат ее модуля |Ψ|² и вероятность обнаружения частицы.

Атом водорода по теории Шредингера

Уравнение Шредингера позволяет решить вопрос о строении водородоподобного атома, т. е. атома, который состоит из положительно заряженного ядра с зарядом +Ze и одного электрона. Потенциальная энергия взаимодействия электрона с ядром, согласно формуле (2.14), равна:



где Z - порядковый номер элемента в таблице Менделеева (для атома водорода = 1);
    e - заряд электрона;
    r - расстояние между электроном и ядром:  (см. формулу (1.1));
      - электрическая постоянная.

Если подставить (5.17) в уравнение Шредингера (5.16), то окажется, что это уравнение имеет решение не при всех отрицательных значениях электрона E, а только таких, которые удовлетворяют условию: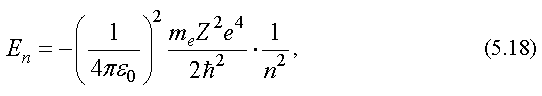



где n = 1, 2, 3, ... - целое число.

Заметим, что формула (5.18) совпадает с формулой (5.11), полученной в теории Бора.

Из формулы (5.18) следует, что энергия электрона в атоме квантуется.

Найденная при этих значениях энергии волновая функция Ψ зависит от трех квантовых чисел:

n - главное квантовое число, n = 1, 2, 3, ...;
l - орбитальное квантовое число, l = 1, 2, 3, ..., (n -1);
m_L - магнитное квантовое число, m_L = -l , -l +1, ..., 0, ..., (l -1), l .

Волновая функция определяет состояние электрона в атоме, а квадрат ее модуля - вероятность обнаружения электрона в единице объема (см. (5.14)).

Вероятность обнаружения электрона в различных частях атома различна. Электрон при своем движении как бы "размазан" по всему объему, образуя электронное облако. Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число m_L характеризует ориентацию электронного облака в пространстве.

В квантовой физике, по аналогии с спектроскопией, состояние электрона, характеризующееся квантовым числом l = 0, называется S - состоянием, l = 1 - p - состоянием, l = 2 - d - состоянием и т. д. Для обозначения различных состояний электрона в атоме используют следующие обозначения: значения главного квантового числа указывают перед условным обозначением орбитального квантового числа. Например, электроны в состояниях n = 1, l = 0 обозначаются 1S, при n = 2, l = 1 обозначаются 2p и т. д.

Квантовые числа позволяют компактно описать закономерности в спектре испускания (поглощения) атома водорода.

24, Модель атома Резерфорда (Ядерная или Планетарная модель атома)

Рассеяние отдельных α-частиц на большие углы Резерфорд объяснил тем, что положительный заряд в атоме не распределен равномерно в шаре радиусом 10^-10м, как предполагали ранее, а сосредоточен в центральной части атома (атомном ядре) в области значительно меньших размеров. Расчеты Резерфорда показали, что для объяснения опытов по рассеянию α-частиц нужно принять радиус атомного ядра равным примерно 10^-15м.

Резерфорд предположил, что атом устроен подобно планетарной системе. Как вокруг Солнца на больших расстояниях от него обращаются планеты, так электроны в атоме о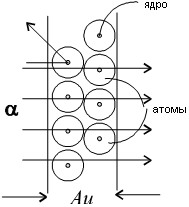бращаются вокруг атомного ядра. Радиус круговой орбиты самого далекого от ядра электрона и есть радиус атома. Такая модель атома была названа планетарной моделью.

Планетарная модель атома объясняет основные закономерности рассеяния заряженных частиц.

Так как большая часть пространства в атоме между атомным ядром и обращающимися вокруг него электронами пуста, быстро заряженные частицы могут почти свободно проникать через довольно значительные слои вещества, содержащие несколько тысяч слоев атомов.

При столкновениях с отдельными электронами быстрые заряженные частицы испытывают рассеяние на очень большие углы, так как масса электрона мала. Однако в тех редких случаях, когда быстрая заряженная частица пролетает на очень близком расстоянии от одного из атомных ядер, под действием силы электрического поля атомного ядра может произойти рассеяние заряженной частицы на любой угол до 180°.