Шпора к экзамену 2 курс 2сем.. 1, Система уравнений Максвела в интегральной форме
 Скачать 1.11 Mb. Скачать 1.11 Mb.
|
[править] Вывод формулы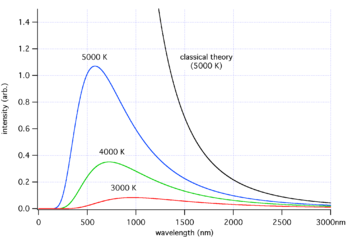 Зависимость испускательной способности абсолютно черного тела от длины волны для разных температур (выделены цветом) и её вид, исходя из классических рассуждений Релея и Джинса (черный цвет) Основываясь на законе о равнораспределении энергии по степеням свободы: на каждое электромагнитное колебание приходится в среднем энергия, складываемая из двух частей kT. Одну половинку вносит электрическая составляющая волны, а вторую — магнитная. Само по себе, равновесное излучение в полости, можно представить как систему стоячих волн. Количество стоячих волн в трехмерном пространстве дается выражением: В нашем случае скорость v следует положить равной c, более того, в одном направлении могут двигаться две электромагнитные волны с одной частотой, но со взаимно перпендикулярными поляризациями, тогда (1) в добавок следует помножить на два: Итак, Релей и Джинс, каждому колебанию приписали энергию . Помножив (2) на ,получим плотность энергии, котрая приходится на интервал частот dω: тогда самоочевидно: Зная связь испускательной способности абсолютно черного тела f(ω,T) с равновесной плотностью энергией теплового излучения Выражения (3) и (4), называют формулой Релея — Джинса. [править] Ультрафиолетовая катастрофаФормулы (3) и (4) удовлетворительно согласуются с экспериментальными данными лишь для больших длин волн, на более коротких волнах согласие с экспериментом резко расходится. Более того интегрирование (3) по ω в пределах от 0 до для равновесной плотности энергии u(T) дает бесконечно большое значение. Этот результат получиший название ультрафиолетовой катастрофы, очевидно входит в противоречие с экспериментом: равновесие между излучением и излучающим телом должно устанавливается при конечных значениях u(T). Однако ошибки в выводе формулы Релея — Джинса, с классической точки зрения — нет. Очевидно несогласие с экспериментом вызвано некими закономерностями, которые несовместимы с классической физикой. Эти закономерности были определены Максом Планком: в 1900 году ему удалось найти вид функции u(ω,T), соответствующий опытным данным, в дальнейшем называемую формулой Планка. Формула Планка — выражение для спектральной плотности мощности излучения абсолютно чёрного тела, которое было получено Максом Планком для равновесной плотности излучения u(ω,T). После того как вывод Релея — Джинса для излучения абсолютно черного тела, столкнулся с ультрафиолетовой катастрофой (расходимость при больших частотах), стало ясно, что классическая физика не в силах объяснить его излучение. Для вывода формулы Планк, в 1900 году сделал предположение, о том что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с частотой излучения выражением: По сути это было «рождение» фотона. Коэффициент пропорциональности в последствии назвали постоянной Планка, = 1.054 · 10-34 Дж·с. [править] Вывод для абсолютно черного тела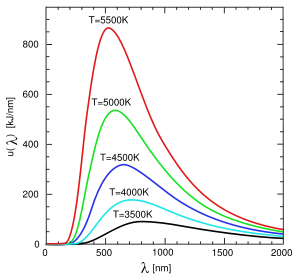 Излучение абсолютно чёрного тела Выражение для средней энергии колебания частотой ω дается выражением: Количество стоячих волн в трехмерном пространстве равно: перемножив (1) и (2), получим плотность энергии, приходящуюся на интервал частот dω: Зная связь испускательной способности абсолютно чёрного тела f(ω,T) с равновесной плотностью энергией теплового излучения Выражения (3) и (4)носят название формулы Планка. Испускательную способность АЧТ, выраженную через длину волны λ т.е. можно выразить используя соотношение: |
