|
|
Шпора к экзамену 2 курс 2сем.. 1, Система уравнений Максвела в интегральной форме
[править] История
В 1924 году французский физик Л. де Бройль (L. de Broglie) высказал гипотезу о том, что установленный ранее для фотонов корпускулярно-волновой дуализм присущ всем частицам — электронам, протонам, атомам и так далее, причём количественные соотношения между волновыми и корпускулярными свойствами частиц те же, что и для фотонов. Таким образом, если частица имеет энергию E и импульс, абсолютное значение которого равно p, то с ней связана волна, частота которой ν = E / h и длина λ = h / p. Эти волны и получили название Волны де Бройля.
[править] Физика
Для частиц не очень высокой энергии, движущихся со скоростью (скорости света), импульс равен p = mv (где m — масса частицы), и λ = h / mv. Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и её скорость. Например, частице с массой в 1 г, движущейся со скоростью 1 м/с, соответствует волна де Бройля с 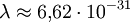 м, что лежит за пределами доступной наблюдению области. Поэтому волновые свойства несущественны в механике макроскопических тел. Для электронов же с энергиями от 1 эВ до 10 000 эВ длина Волны де Бройля лежит в пределах от
1 нм до 10-2 нм, то есть в интервале длин волн рентгеновского излучения. Поэтому волновые свойства электронов должны проявляться, например, при их рассеянии на тех же кристаллах, на которых наблюдается дифракция рентгеновских лучей.
Первое подтверждение гипотезы де Бройля было получено в 1927 году в опытах американского физика К. Дэвиссона и Л. Джермера. Пучок электронов ускорялся в электрическом поле с разностью потенциалов 100—150 В (энергия таких электронов 100—150 эВ, что соответствует нм) и падал на кристалл никеля, играющий роль пространственной дифракционной решётки. Было установлено, что электроны дифрагируют на кристалле, причём именно так, как должно быть для волн, длина которых определяется соотношением де Бройля.
Подтвержденная на опыте идея де Бройля о двойственной природе микрочастиц — корпускулярно-волновом дуализме — принципиально изменила представления об облике микромира. Поскольку всем микрообъектам (по традиции за ними сохраняется термин «частица») присущи и корпускулярные и волновые свойства, то, очевидно, любую из этих «частиц» нельзя считать ни частицей, ни волной в классическом понимании. Возникла потребность в такой теории, в которой волновые и корпускулярные свойства материи выступали бы не как исключающие, а как взаимно дополняющие друг друга. В основу такой теории — волновой, или квантовой, механики — и легла концепция де Бройля. Это отражается даже в названии «волновая функция» для величины, описывающей в этой теории состояние системы. Квадрат модуля волновой функции определяет вероятность состояния системы, и поэтому о волнах де Бройля часто говорят как о волнах вероятности (точнее, амплитуд вероятности). Для свободной частицы с точно заданным импульсом p (и энергией ), движущейся вдоль оси x, волновая функция имеет вид:
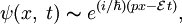
где t — время, .
В этом случае | ψ | 2 = const, то есть вероятность обнаружить частицу в любой точке одинакова
Корпускулярно-волновой дуализм — это теория о том, что любое вещество (электромагнитное излучение, физическое тело, атом и т.п.) представляется на микроуровне одновременно и как мельчайшие частицы (корпускулы), и как волны
22, Принцип неопределённости Гейзенбе́рга (или Га́йзенберга ) — в квантовой механике так называют принцип, дающий нижний (ненулевой) предел для произведения дисперсий величин, характеризующих состояние системы.
Обычно принцип неопределенности иллюстрируется следующим образом. Рассмотрим ансамбль невзаимодействующих эквивалентных частиц, приготовленных в определенном состоянии, с каждой из которых производятся два последовательных измерения. Первое определяет импульс частицы, а второе, сразу после этого, её координату. Измерение импульса даст некоторое распределение с характерной дисперсией. Второе же измерение даст распределение значений, дисперсия которого d²q будет связана с дисперсией импульса d²p так, что  .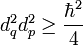
Стоит отметить, что дисперсии, участвующие в этом неравенстве, отражают характеристики состояния, а не процесса измерения. Вопреки распространенной ошибке, принцип неопределенности ничего не говорит о предельной точности измерений.
В общем смысле, соотношение неопределённости возникает между любыми переменными состояния, определяемыми некоммутирующими операторами. Это - один из краеугольных камней квантовой механики, который был открыт Вернером Гейзенбергом в 1927 г.[источник?]
Принцип неопределённости в квантовой механике иногда объясняется таким образом, что измерение координаты обязательно влияет на импульс частицы. По-видимому, сам Гейзенберг предложил это объяснение, по крайней мере первоначально. То, что влияние измерения на импульс несущественно, может быть показано следующим образом: рассмотрим ансамбль (невзаимодействующих) частиц приготовленных в одном и том же состоянии; для каждой частицы в ансамбле мы измеряем либо импульс, либо координату, но не обе величины. В результате измерения мы получим, что значения распределены с некоторой вероятностью, и для дисперсий dp и dq верно отношение неопределённости.
Отношения неопределенности Гейзенберга — это теоретический предел точности любых измерений. Они справедливы для так называемых идеальных измерений, иногда называемых измерениями фон Неймана. Они тем более справедливы для неидеальных измерений или измерений Ландау.
Соответственно, любая частица (в общем смысле, например несущая дискретный электрический заряд) не может быть описана одновременно как «классическая точечная частица» и как волна. (Сам факт того, что какое-либо из этих описаний может быть справедливо, по крайней мере в отдельных случаях, называют корпускулярно-волновым дуализмом). Принцип неопределённости, в виде, первоначально предложенном Гейзенбергом, верен в случае, когда ни одно из этих двух описаний не является полностью и исключительно подходящим, например частица в коробке с определённым значением энергии; то есть для систем, которые не характеризуются ни каким-либо определённым «положением» (какое-либо определённое значение расстояния от потенциальной стенки), ни каким-либо определённым значением импульса (включая его направление).
Существует точная, количественная аналогия между отношениями неопределённости Гейзенберга и свойствами волн или сигналов. Рассмотрим переменный во времени сигнал, например звуковую волну. Бессмысленно говорить о частотном спектре сигнала в какой-либо момент времени. Для точного определения частоты необходимо наблюдать за сигналом в течение некоторого времени, таким образом теряя точность определения времени. Другими словами, звук не может иметь и точного значения времени, как например короткий импульс, и точного значения частоты, как, например, в непрерывном чистом тоне. Временно́е положение и частота волны во времени походят на координату и импульс частицы в пространстве.
|
|
|
Скачать 1.11 Mb.