Шпора к экзамену 2 курс 2сем.. 1, Система уравнений Максвела в интегральной форме
 Скачать 1.11 Mb.
|
Переход к формулам Релея—Джинса.Формула Планка точно согласуется с экспериментальными данными во всем интервале частот от 0 до . При малых частотах (больших длинах волн), когда  можно разложить экспоненту по . В результате получим, что  , тогда (3) и (4) переходят в формулу Релея—Джинса. и  18, Законы фотоэффектаВнешним фотоэффектом называется вырывание электронов из вещества под действием света. Законы фотоэффекта изучали с помощью схемы с двухэлектродной лампой с освещаемым катодом (рис. 5.1). Под действием света из катода вырываются электроны, которые под действием электрического поля перемещаются к аноду, создавая анодный ток.  Рис.5.1 Вольтамперная характеристика, полученная с помощью такой схемы при неизменном световом потоке Ф, приведена на рис. 5.2. 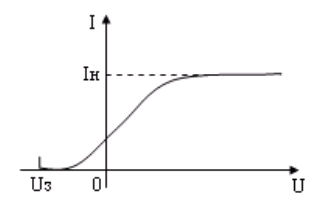 Рис.5.2 Из анализа вольтамперных характеристик получены законы фотоэффекта.
Величина v0 зависит от химической природы вещества и состояния его поверхности.
Iнас = Кст · Ф - закон Столетова, где Кст - коэффициент пропорциональности. Эти законы невозможно было объяснить с классической точки зрения, согласно которой электрическая компонента электромагнитной волны вызывает вынужденные колебания свободных электронов в металле, сообщая им энергию, достаточную для вылета. Тогда максимальная кинетическая энергия фотоэлектронов должна быть пропорциональна квадрату амплитуды световой волны (см. (3.14)), т. е. должна зависеть от светового потока, что противоречит опытным фактам. 5.2. Уравнение Эйнштейна для фотоэффектаОбъяснение законов фотоэффекта дал в 1905 г. немецкий ученый Альберт Эйнштейн на основе гипотезы световых квантов. Вслед за Планком он предположил, что, если излучение энергии атомами происходит дискретно в виде порций или квантов, то ее распространение в пространстве и поглощение веществом происходит порциями (квантами). Энергия кванта равна: где v - частота падающего света, h = 6.63 • 10 -34 (Дж•с) - постоянная Планка. Заметим, что в механике есть величина, которую называют действием. Она имеет размерность "энергия × время". Поэтому постоянную Планка иногда называют квантом действия. Кванты света называются фотонами. Поэтому с квантовой точки зрения свет представляет собой поток фотонов. Уравнение Эйнштейна объясняет все закономерности внешнего фотоэффекта. Оно представляет собой по сути дела закон сохранения энергии. Каждый фотон взаимодействует с одним электроном и передает ему энергию hv. Эта энергия затрачивается на то, чтобы совершить работу выхода электрона из металла - A и сообщить ему кинетическую энергию. Причем, если электрон вырывается с поверхности металла, а не из глубины, то кинетическая энергия электрона будет максимальной. Уравнение Эйнштейна для фотоэффекта имеет вид  Покажем, как из уравнения Эйнштейна (5.2) можно объяснить законы фотоэффекта.
Если частота падающего света больше или равна красной границе , то фотоэффект наблюдается, иначе - нет. Работа выхода зависит от химической природы вещества. Ее можно найти в справочнике. Значение работы выхода обычно указывают в электронвольтах . Из формулы (3.21) следует, что  Длину волны λ тоже называют красной границей фотоэффекта.
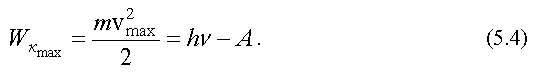 Из формулы (5.4) следует, что максимальная кинетическая энергия вылетевших электронов линейно зависит от частоты падающего света. Экспериментальное значение можно найти, зная задерживающую разность потенциалов (рис. 5.2): , где e - заряд электрона, Uз - задерживающая разность потенциалов.
При этом изменяется число электронов, взаимодействующих с фотонами nф, а значит изменяется фототок. Фототок насыщения соответствует такому состоянию, когда все вылетевшие из катода электроны попадут на анод. Следовательно, можно написать цепочку пропорциональностей . Если перейти от пропорциональности к равенству, получим формулу для записи закона Столетова  Таким образом, в явлении фотоэффекта проявляется квантовая природа света. 19, Давление светаПусть на единицу плошади поверхности в единицу времени нормально падает N (1/м2с) фотонов. Пусть Nп фотонов поглощается, a N0 - отражается. Тогда  (1)где a=Nп/N и =N0/N - коэффициенты поглощения и отражения падающего излучения. Поглощенный фотон с импульсом 2p передаст поверхности импульс, равный p, а отраженный – 2p. Тогда импульс р, передаваемый ед.площади поверхности в ед.времени N фотонами будет равен  (2)Учитывая, что импульс фотона p связан с его энергией соотношением Р =/с , получим  (3)где E =Nh (Дж/м2с) - энергетическая освещенность поверхности или интенсивность падающего излучения (света):  (4)где <> -объемная плотность энергии ЭМ-волны или фотонов. Получаем для давления света(P->P )  (5)Если обозначить n=N/c (1/м3) - концентрацию фотонов в ЭМ-волне, то  Фотоном называется элементарная частица - квант электромагнитного поля. Отличие фотона от других элементарных частиц состоит в том, что фотон всегда движется со скоростью Фотоны как квазичастицы света обладают не только энергией но и массой т. Масса фотона находится с помощью выражения для энергии микрочастицы в релятивистской механике: е = тс2. Следовательно,  — масса фотона. (9.28) Введенное таким способом понятие массы фотона существенно отличается от понятия массы обычных микрочастиц. Фотон не обладает массой покоя, т. е. для него mп = 0. И  мпульс фотонаИмпульс р фотона можно выразить через волновой вектор k=(2n/X)n (n — единичный вектор нормали к фронту волны), т. е.  (9.29)Наличие у фотона импульса экспериментально проявляется в давлении света на твердые тела и газы .Фотон как элементарная частица обладает спином, равным 1 (в единицах Н), и, следовательно, относится к классу бозонов 20, 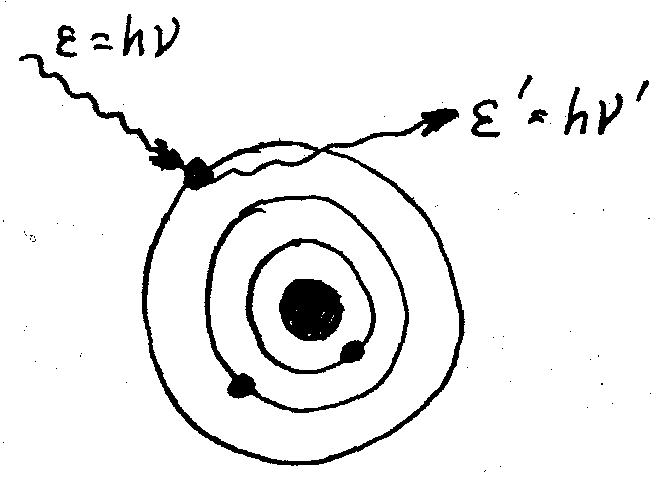 Рэлеевское и комптоновское рассеяние света. При взаимодействии света с атомами вещества фотоны могут рассеиваться двумя способами: 1. Упруго, без изменения частоты ' или '. Такое рассеяние называют рэлеевским. 2. Неупруго, c изменением частоты '<или '< ('>). Такое рассеяние называют комптоновским. А.Г.Комптон(1923), впервые наблюдавший изменение длины волны рентгеновских лучей при их рассеянии на различных веществах, объяснил это явление рассеянием Х-лучей на электронах самых верхних оболочек(орбит) атома. Эти электроны наиболее слабо связаны с атомом. При рассеянии фотон отдает часть своей энергии слабосвязанному электрону и его энергий ' =h' и частота ' при рассеянии уменьшаются, а длина волны рассеянного фотона '=c/' увеличивается. Описание эффекта КомптонаП 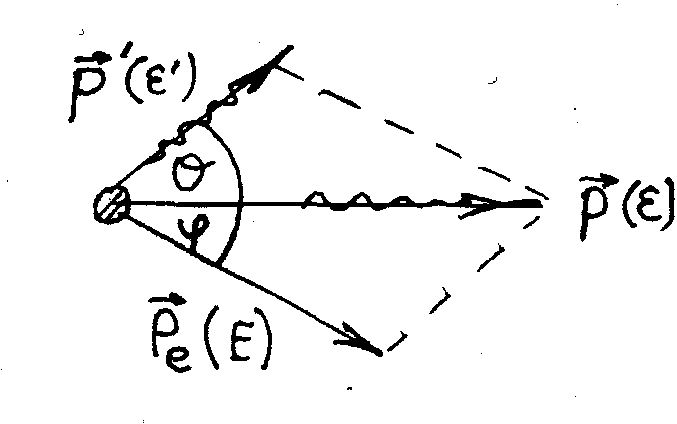 усть на электрон с энергией покоя E0=m0c2 падает фотон с импульсом P. При рассеянии фотон передаст часть своей энергии электрону и его импульс и энергия станут равными р' и '. Электрон приобретет импульс и его энергия станет равной E. Согласно релятивистскому тож-деству(pec)2=E2-E02 энергию электрона можно представить в виде Процесс рассеяния фотона на электроне можно рассматривать как столкновение двух шариков. Такой процесс описывается законами сохранения энергии и импульса 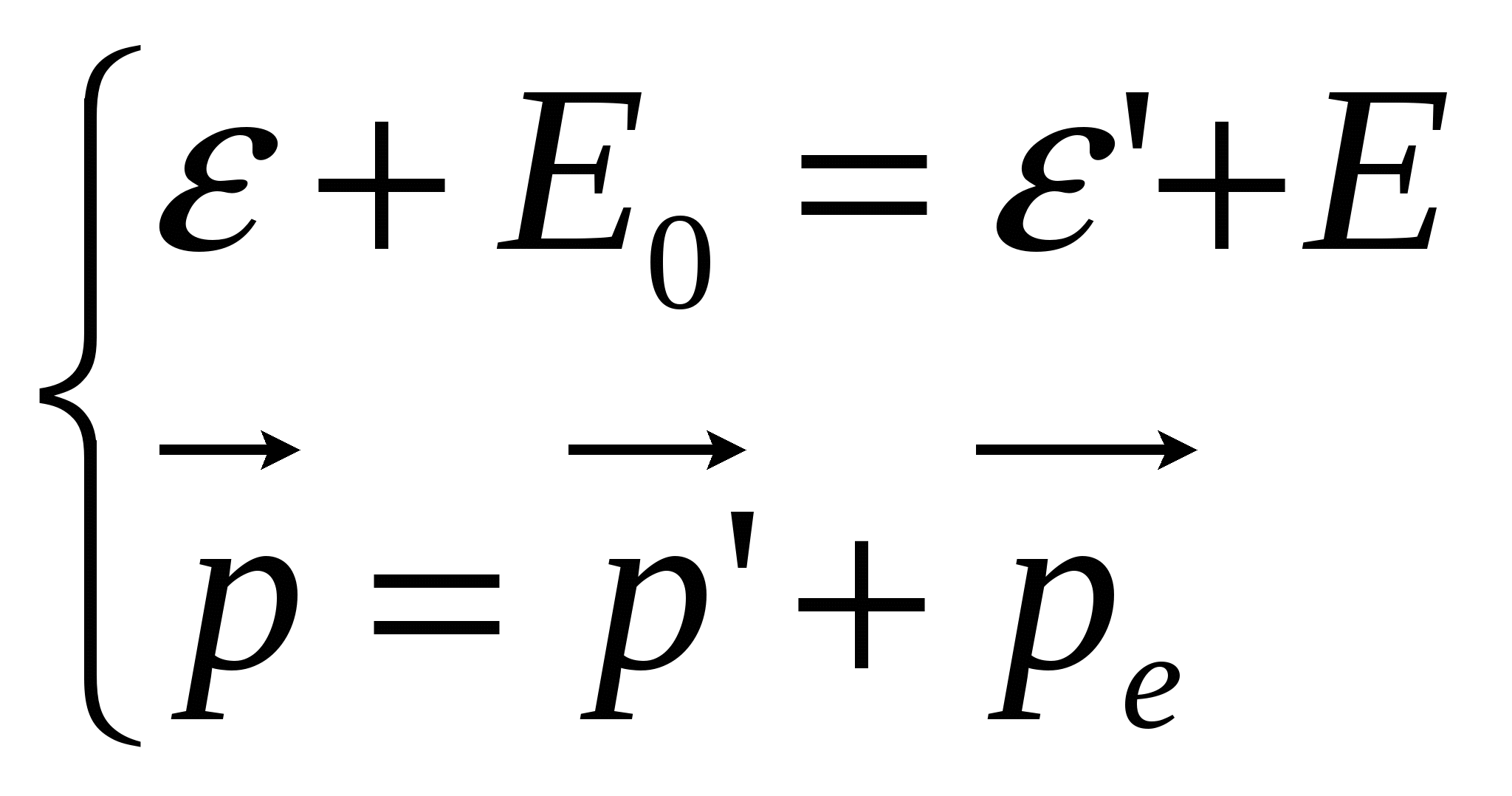 ———>  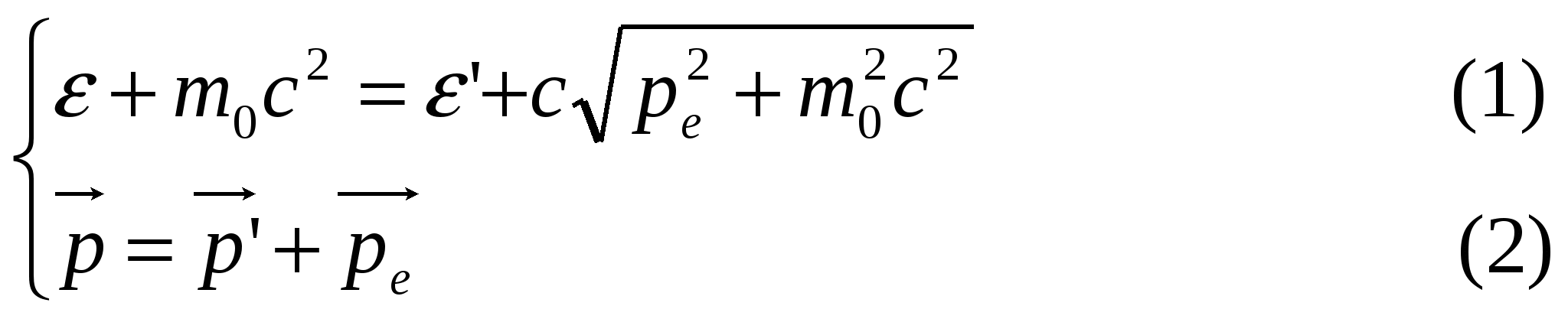Разделим (1) на с и с учетом 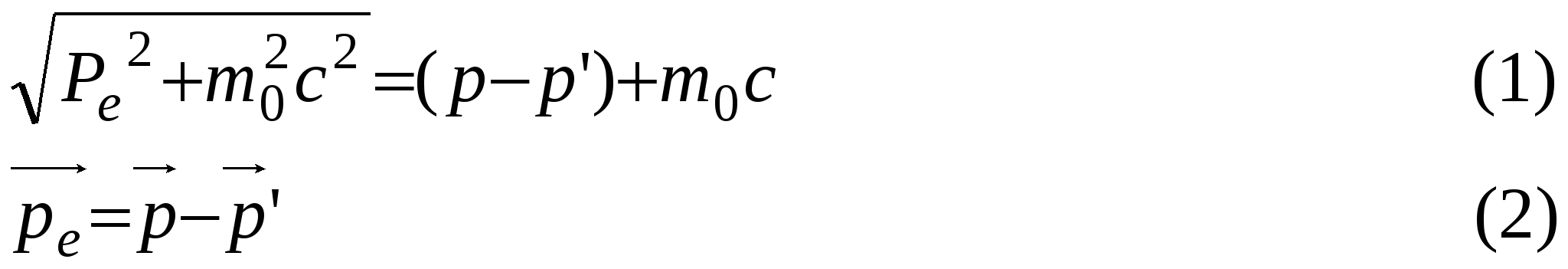 запишем (1) и (2) в виде Возведем равенства (1) и (2) в квадрат  (1) (2)Из сопоставления (1) и (2) следует  (3)Подставляя для фотона  , получим (4)откуда  Получили  (5)где величина =h/m0с называется комптоновской длиной волны для частицы с массой покоя m0. Для электрона е=2,436 пм.  ;  (6)Формулу (3), используя теорему синусов, можно записать в другом виде. Выражая импульс рассеянного фотона P' через импульс P падающего фотона и подставляя Р' в формулу (3) после преобразований получим  (7)где /E0 = - отношения энергии падающего фотона к энергии покоя электрона, комптон. длина волны, - длина волны падающего фотона. волны, - длина волны падающего фотона. 21, Во́лны де Бро́йля — волны, связанные с любой микрочастицей и отражающие их квантовую природу. |