1. скорость химической реакции

• Название: 1. скорость химической реакции
• Анкор: Khim_kinetika_i_ravnovesie.doc
• Дата: 28.01.2017
• Размер: 1.62 Mb.
• Имя файла: Khim_kinetika_i_ravnovesie.doc
• Тип: Документы; #874
• страница: 5 из 9

1.7. Последовательность расчета кинетических данных
Целью любого кинетического исследования является нахождение кинетического уравнения и определение его параметров. Кинетическое исследование состоит из следующих этапов:

1) получение экспериментальных данных для построения графика кривых С = f() при нескольких температурах;

2) расчет частных порядков по каждому из реагирующих веществ и определение суммарного порядка реакции;

3) определение формального кинетического уравнения и проверка его соответствия экспериментальным данным;

4) определение значения констант скорости реакции при различных температурах;

5) расчет энергии активации и предэкспоненциального множителя в уравнении Аррениуса.
Определение кинетического порядка реакции

Существует несколько способов определения порядка реакции. Рассмотрим два простейших из них для необратимых реакций первого и второго порядков.

1. Метод подбора. Метод заключается в подстановке экспериментальных данных в уравнение первого и второго порядков и выяснении, какое из этих уравнений приводит к постоянному значению константы скорости реакции. Ели ни одно из них не дает постоянного результата, то реакция является более сложной.

2. Графический метод. Строится график, выражающий зависимость различных значений концентраций от времени в соответствии с различными кинетическими уравнениями.

Так, для реакции первого порядка линейная зависимость получается в координатах lg(ах) и  (см. рис.6), второго порядкав координатах 1/(ах) и  (рис.8) и lg(в(ах)/а(вх)) и  (рис.9).
Определение константы скорости реакции
Константа скорости реакции может быть рассчитана, если известен порядок реакции из соответствующего кинетического уравнения. Известны несколько методов расчета константы скорости реакции. Важнейшие из них:

1) метод подстановки концентраций реагирующих веществ или продуктов реакции, полученных аналитически в разные моменты времени, в соответствующее кинетическое уравнение реакции. После расчета значения констант для разных времен () проводят их усреднение;

2) графический метод применяется, когда имеются удобные линейные формы зависимости величины концентраций и их производных от времени реакции.

Например, для реакции первого порядка кинетическое уравнение имеет вид:

lg(ах) = k/2,303 + lgа.
Это уравнение прямой линии с угловым коэффициентом k/2,303 (рис.16). Угловой коэффициент есть tg.

Из графика находим:

lg = k/2,303, lg() = k/2,303,

откуда

k = 2,303^.lg().
Далее по экспериментальным данным строим график зависимости lg(ах) = f() и по тангенсу угла наклона (учитывая масштабы координат) определяем константу скорости реакции.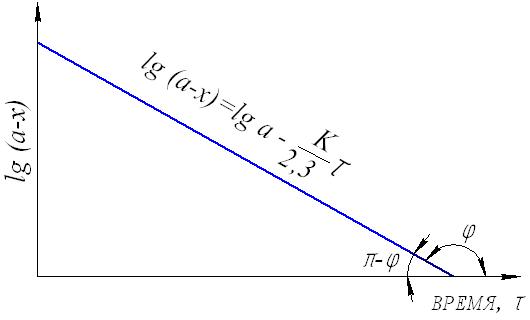



Рис.16. Графический расчет константы скорости

необратимой реакции первого порядка
Аналогичным образом можно определить константу скорости реакции второго порядка.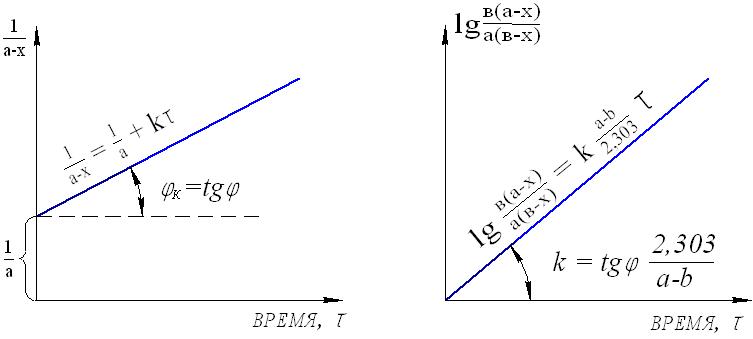


а) б)

Рис.17. Графический расчет константы скорости необратимой реакции второго порядка:

а) для случая равенства концентраций реагирующих веществ (а = в)

б) для общего случая (а  в)
1.8. Примеры решения задач
Пример 1. Во сколько раз следует увеличить концентрацию водорода в системе

N₂  3H₂  2NH₃

чтобы скорость реакции возросла в 100 раз?
Решение. Выражение скорости данной реакции

v = k[N₂][H₂]³.

В начальный момент времени

v₀ = k[N₂]₀[H₂]₀³.

Примем увеличение концентрации водорода за х,

тогда

v₁=k[N₂]₀[хH₂]³ = х³k[N₂]₀[H₂]₀³ = х³v₀= 100v_0,

откуда

х³ = 100,

и тогда увеличение концентрации водорода должно составить

х = 4,64.
Пример 2. Как изменится скорость прямой реакции, если давление в системе увеличить в три раза?

N₂  3H₂  2NH₃

Решение. Увеличение давления в три раза равнозначно уменьшению объема в три раза и, соответственно, увеличению концентрации всех веществ в три раза.

Скорость реакции в начальный момент времени:

v₀ = k[N₂]₀[H₂]₀³;

после увеличения давления

v₁ =k[3N₂][3H₂]³ = 3 3³ k[N₂]₀[H₂]₀³ = 81v_0,

т.е., скорость прямой реакции увеличится в 81 раз.
Пример 3. Повышение температуры с 50⁰С до 70⁰С вызывает увеличение скорости реакции в 9 раз. Найти температурный коэффициент реакции.

Решение. Выразим температурный коэффициент реакции из уравнения Вант-Гоффа:

γ ^(t1-t2)/10 = v₂/v₁,

и получаем

γ^(70-50)/10 = 9, γ² = 9, γ = 3.
Пример 4. Вычислить энергию активации и константу скорости химичес-

кой реакции

CO + H₂O  H₂ + CO₂

при 303 К (Т₃), если константы скорости реакции при 288 К (Т₁) и 313 К (Т₂) соответственно рввны 3,1 10^-4 и 8,15 10^-3 моль/л.
Решение. Из уравнения Аррениуса следует

Еа = 2,3RT₁T₂lg(k₂/k₁)/(T₂T₁).
Подставляя полученные значения, получаем:

Еа = 2,3 8,31 288 313 lg(8,15^.10^-3/3,1 10^-4)/(313288) = 97848 Дж/моль.

Константу скорости реакции при 303 К можно найти из соотношения

lg(k₃/k₁) = Еа(Т₃Т₁)/(2,3RT₃Т₁) или lg(k₂/k₃) = Еа(Т₂Т₃)/(2,3RT₂Т₃).
Подставляя имеющиеся значения в любую из этих формул, получаем:

k₃ = 2,34 10^-3 л моль^-1 мин^-1.
Пример 5. При температуре 10 ⁰С реакция заканчивается через 120 секунд а, при 30⁰С  через 30 секунд. Найти энергию активации.

Решение. Очевидно, что k₍₃₀₎/k₍₁₀₎ = ₍₁₀₎/₍₃₀₎, и тогда, подставляя значения в формулу Еа = 2,3RT₁T₂lg(k₂/k₁)/(T₂T₁), получаем:

Еа = 2,3 8,31(273+10)(273+30)lg(120/30)/(3010) = 49336 Дж/моль

или 49,3 кДж/моль.
Пример 6. Константа омыления этилового эфира уксусной кислоты едким натром при 100С равна 2,38 л/моль^.мин. Определить время, необходимое для омыления 90 уксусно-этилового эфира, если смешать при этой температуре 1л 0,05 молярного раствора эфира с 1л 0,05 молярного раствора NaOH.

Решение. Реакция

CH₃COOC₂H₅ + NaOH = CH₃COONa + C₂H₅OH

является реакцией второго порядка; концентрации эфира и щелочи равны и можно воспользоваться уравнением:

k = x/( a(ax)),

откуда

 = x/(k a(ax)).

Учитывая взаимное разбавление растворов в два раза и превращение уксусно-этилового эфира на 90, получаем:

а = 0,05/2 = 0,025моль/л; х = 0,05 0,9/2 = 0,0225моль/л.
Тогда время реакции составит

 = 0,0225/((2,38 0,025(0,0250,225)) = 151,2 мин.

2. ХИМИЧЕСКОЕ РАВНОВЕСИЕ
2.1. Обратимые и необратимые реакции
Одной из важнейших характеристик химической реакции является глубина (степень) превращения, показывающая, насколько исходные вещества превращаются в продукты реакции. Чем она больше, тем экономичнее можно проводить процесс. Глубина превращения, помимо других факторов, зависит от обратимости реакции.

Обратимые реакции, в отличие от необратимых, протекают не до конца: ни одно из реагирующих веществ не расходуется полностью. Одновременно идет взаимодействие продуктов реакции с образованием исходных веществ.

Рассмотрим примеры:

1) в замкнутый сосуд при определенной температуре введены равные объемы газообразного йода и водорода. Если столкновения молекул этих веществ происходят с нужной ориентацией и достаточной энергией, то химические связи могут перестроиться с образованием промежуточного соединения (активированный комплекс, см. п.1.3.1). Дальнейшая перестройка связей может привести к распаду промежуточного соединения на две молекулы йодистого водорода. Уравнение реакции:

H₂  I₂  2HI
Но молекулы йодистого водорода также будут беспорядочно сталкиваться с молекулами водорода, йода и между собой. При столкновении молекул HI ничто не помешает образоваться промежуточному соединению, которое затем может разложиться на йод и водород. Этот процесс выражается уравнением:
2HI  H₂ + I₂
Таким образом, в этой системе одновременно будут протекать две реакции  образование йодистого водорода и его разложение. Их можно выразить одним общим уравнением

H₂ + I₂  2HI
Обратимость процесса показывает знак .

Реакция, направленная в данном случае в сторону образования йодистого водорода, называется прямой, а противоположная  обратной.

2) если смешать два моль диоксида серы с одним моль кислорода, создать в системе условия, благоприятствующие протеканию реакции, и по истечении времени провести анализ газовой смеси, то результаты покажут, что в системе будут присутствовать как SO₃ – продукт реакции, так и исходные вещества – SO₂ и O₂. Если в те же условия в качестве исходного вещества поместить оксид серы (+6), то можно будет обнаружить, что часть его разложится на кислород и оксид серы (+4), причем конечное соотношение между количествами всех трех веществ будет такое же, как и в том случае, когда исходили из смеси диоксида серы и кислорода.

Таким образом, взаимодействие диоксида серы с кислородом также является одним из примеров обратимой химической реакции и выражается уравнением

2SO₂ + O₂  2SO₃
3) взаимодействие железа с соляной кислотой протекает согласно уравнению:

Fe + 2HCL  FeCL₂ + H₂
При достаточном количестве соляной кислоты реакция закончится, когда

все железо израсходуется. Кроме того, если попытаться провести эту реакцию в обратном направлении – пропускать водород через раствор хлорида железа, то металлического железа и соляной кислоты не получится – эта реакция не может идти в обратном направлении. Таким образом, взаимодействие железа с соляной кислотой – необратимая реакция.

Однако, следует иметь ввиду, что теоретически любой необратимый процесс можно представить протекающим в определенных условиях обратимо, т.е. в принципе все реакции можно считать обратимыми. Но очень часто одна из реакций явно преобладает. Это бывает в тех случаях, когда продукты взаимодействия удаляются из сферы реакции: выпадает осадок, выделяется газ, при ионообменных реакциях образуются практически недиссоциирующие продукты; или же когда за счет явного избытка исходных веществ противоположный процесс практически подавляется. Таким образом, естественное или искусственное исключение возможности протекания обратной реакции позволяет довести процесс практически до конца.

Примерами таких реакций могут служить взаимодействие хлорида натрия с нитратом серебра в растворе
NaCL + AgNO₃  AgCl + NaNO₃,
бромида меди с аммиаком
CuBr₂ + 4NH₃  [Cu(NH₃)₄]Br₂,
нейтрализация хлороводородной кислоты раствором едкого натра
HCl + NaOH  NaCl + H₂O.
Это все примеры лишь практически необратимых процессов, так как и хлорид серебра несколько растворим, и комплексный катион [Cu(NH3)₄]²⁺ не абсолютно устойчив, и вода диссоциирует, хотя и в крайне незначительной степени.
2.2. Состояние химического равновесия
В общем виде любую обратимую химическую реакцию можно представить в следующем виде:

aА + bВ  dD + rR,
где a, b, d, rстехиометрические коэффициенты перед соответсвующими веществами.

По закону действующих масс (см. п.1.3.2) скорости прямой и обратной реакций соответственно равны:
v₁ = k₁C_А^аC_В^b, v₂ = k₂C_D^dC_R^r,

где k₁ и k₂константы скоростей, соответственно, прямой и обратной реакций.

В ходе реакции исходные вещества расходуются, их концентрации уменьшаются, соответственно снижается и скорость прямой реакции. Концентрации продуктов в это время растут, и вместе с этим увеличивается скорость обратной реакции. Это приводит к тому, что разность скоростей реакций уменьшается, и, в конце концов, они выравниваются: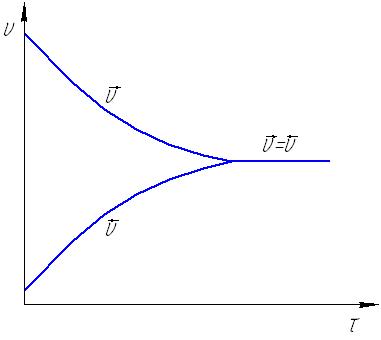


Рис.18. Изменение скоростей прямой и

обратной реакций с течением времени.
Состояние системы, при котором скорости прямой и обратной реакций равны, называется состоянием химического равновесия.
v₁ = v₂  условие химического равновесия
Химическое равновесие называют динамическим. Этим подчеркивается, что при равновесии протекают две реакции  прямая и обратная, но никаких изменений в системе не происходит, т.к. их скорости одинаковы.

Можно сформулировать признаки, которыми характеризуется устойчивое химическое равновесие:

а) при отсутствии внешних воздействий состояние системы остается неизменным во времени;

б) система следует за изменением внешних воздействий, сколь малы бы они ни были. Перемена направления воздействия вызывает перемену направления изменения в системе. Если внешнее воздействие прекращается, система возвращается в исходное состояние. Между воздействием на систему и его результатом существует количественная связь;

в) состояние системы будет одинаковым независимо от того, с какой стороны она подходит к равновесию.

Необходимо ясно понимать, что при равновесии в каждый момент времени количество молекул, образовавшихся в результате взаимодействия исходных веществ, равно количеству молекул, распавшихся в результате обратной реакции. Очевидно поэтому, что в состоянии равновесия концентрации веществ не изменяются; они называются равновесными концентрациями.

Так как при установившемся равновесии v₁  v₂, следовательно,
v₁= k₁C_А^аC_В^b = v₂ = k₂C_D^dC_R^r,

отсюда

k₁k₂ = C_D^dC_R^r  C_А^аC_В^b.
Поскольку константы скоростей реакций при данной температуре постоянны, то постоянным будет и их отношение. Эта постоянная называется константой равновесия данной реакции  Кр. Ее физический смысл в том, что она показывает, во сколько раз константа скорости прямой реакции больше константы скорости обратной реакции. Окончательно получаем:
Кр = k₁k₂ = C_D^dC_R^r  C_А^аC_В^b (2.1)
Таким образом, при постоянной температуре константа равновесия обратимой реакции представляет собой постоянную величину, показывающую то соотношение между концентрациями продуктов реакции (числитель) и исходных веществ (знаменатель), которое устанавливается при равновесии.

Уравнение константы показывает, что в условиях равновесия концентрации всех веществ равновесной системы связаны между собой. Изменение концентрации любого из них влечет за собой изменения концентраций всех остальных веществ; в итоге устанавливаются новые концентрации, но соотношение между ними остается неизменным, равным значению константы равновесия.

Численное значение константы равновесия в первом приближении характеризует выход данной реакции. Выходом реакции называется отношение количества получаемого вещества к такому его количеству, которое получилось бы при протекании реакции до конца. При Кр1 выход реакции велик, потому что при этом C_D^dC_R^rC_А^аC_В^b, т.е. равновесные концентрации продуктов прямой реакции намного больше равновесных концентраций исходных веществ, а это и означает, что выход реакции велик, а, соответственно, при Кр1  незначителен.

В случае гетерогенных реакций в выражение константы равновесия, так же как и в выражение закона действующих масс, входят концентрации только тех веществ, которые находятся в газовой фазе или в растворе. Например, для реакции

С_(тв) + СO_2(г)  2СО_(г)
константа равновесия имеет вид:
Кр = [СО]²[CO₂].


Константа равновесия связана с изменением энергии Гиббса реакции, что выражается соотношением:
G⁰ (Т) =  RTlnKр или Кр = exp[G⁰(Т)RT] (2.2)
Эти уравнения дают возможность, зная G⁰, вычислять константу равновесия и, наоборот, по экспериментально найденному значению константы равновесия определять изменение энергии Гиббса реакции. При подстановке значений R = 8,314 Дж(моль К) и обычной для термодинамических измерений и вычислений температуры 298 К (25⁰С) и переходя к десятичному логарифму, получаем удобную рабочую формулу:
G⁰(298) = 5,71 lgКр (кДж/моль) (2.3)