1. скорость химической реакции
 Скачать 1.62 Mb. Скачать 1.62 Mb.
|
|
Тогда уравнение скорости реакции первого порядка (1.7) будет иметь вид: Решение этого уравнения относительно константы скорости реакции (с переходом к десятичным логарифмам) дает следующее выражение: Из этого выражения видно, что размерность константы скорости реакции первого порядка есть «время –1». Преобразуя уравнение (1.9), можно получить: Если построить график зависимости lg(a–x) от времени, то получим прямую, имеющую отрицательный наклон, равный –k/2,303, и отсекающую на оси ординат отрезок, равный lga (рис.6). То есть, если при экспериментальном исследовании реакции неизвестного порядка график lg(a–x) = f(τ) получается в виде прямой, это значит, что реакция имеет первый порядок. Другая характеристика реакций первого порядка – время превращения исходного продукта наполовину (время полупревращения, τ1/2). Согласно уравнению (1.9) 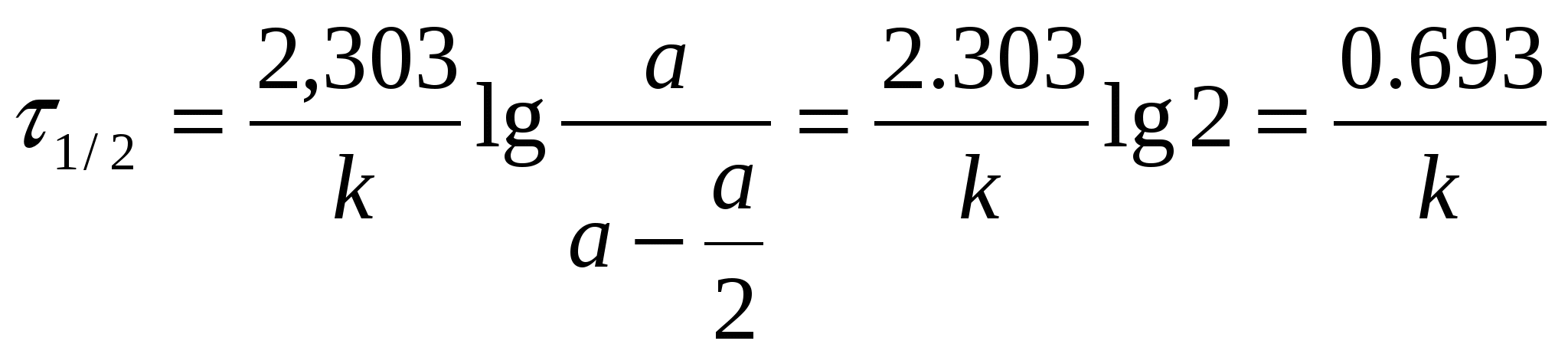 (1.11) (1.11) 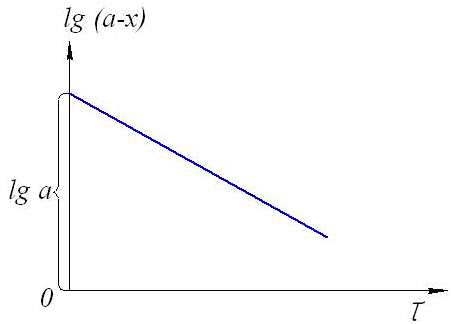 Рис.6. График зависимости lg(ax) от времени для реакции первого порядка На рисунке 7 видно, что время полупревращения постоянно и не зависит от начальной концентрации вещества. Например, если в момент времени имеется 1 моль реагента, то потребуется одинаковое время, чтобы его концентрация понизилась до ½ моль, от ½ до ¼ моль, от ¼ до ⅛ моль и т.д. 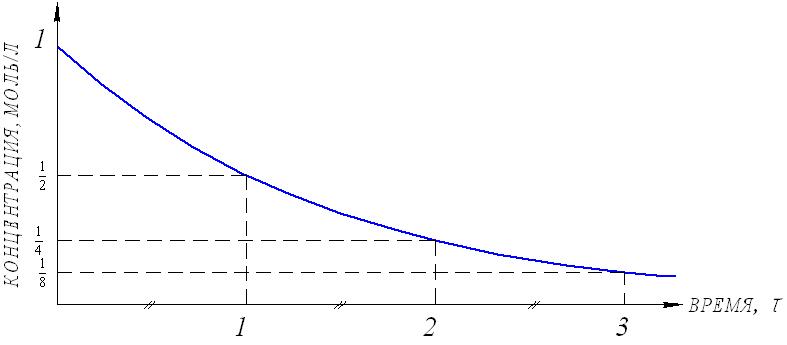 Рис.7. Изменение концентрации реагирующего вещества как функция времени для реакции первого порядка Реакции второго порядка. В общем виде уравнение реакции второго порядка можно записать следующим образом: А + В продукты (1.12) Выражение скорости имеет вид: v = k·CA·CB (1.13) Если концентрации реагентов в начальный момент времени соответственно равны «а» и «в», и если в какой-то момент времени τ x моль/л реагента А взаимодействуют с x моль/л реагента В, то останется (а–x) моль/л реагента А и (b–x) моль/л реагента В. Скорость реакции пропорциональна концентрациям реагентов в каждый момент времени, и выражение превратится в выражение При решении этого уравнения возможны два случая: а) начальные концентрации «а» и «в» равны, тогда выражение скорости будет выглядеть следующим образом: Решение этого уравнения имеет вид: Видно, что константа скорости реакции второго порядка имеет размерность «л моль1 с1»). Уравнение (1.16) можно представить в виде: Если построить график зависимости от времени величины 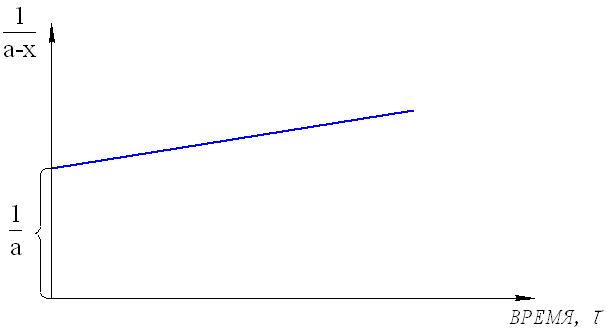 Рис.8. Величина 1/(ах) как функция времени для реакции первого порядка Время полупревращения для реакции второго порядка вычисляем из уравнения (1.16): 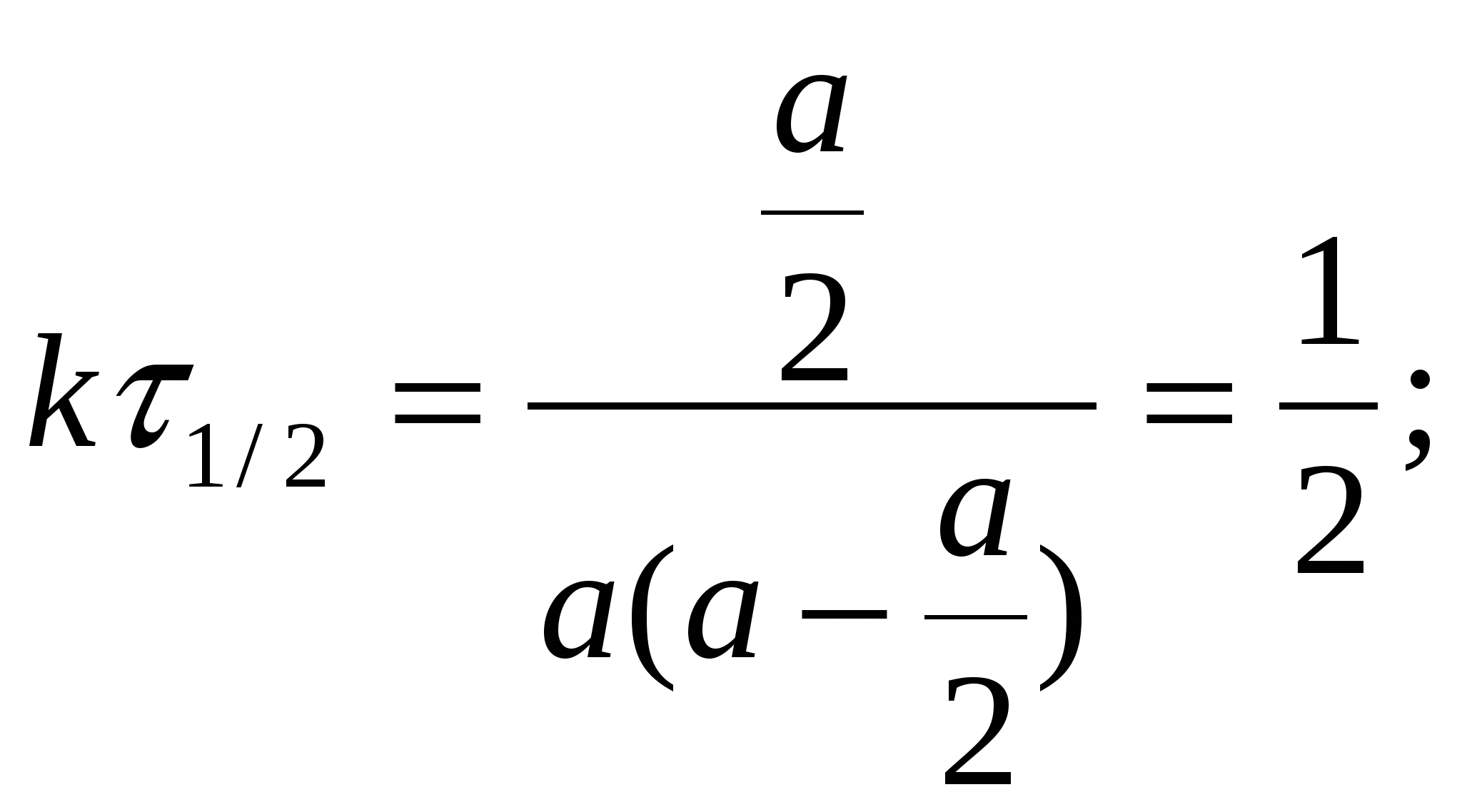 Видно, что время полупревращения для реакции второго порядка обратно пропорционально начальной концентрации. б) начальные концентрации «а» и «в» не равны между собой, тогда выражение скорости будет иметь вид: и решение этого уравнения: График зависимости 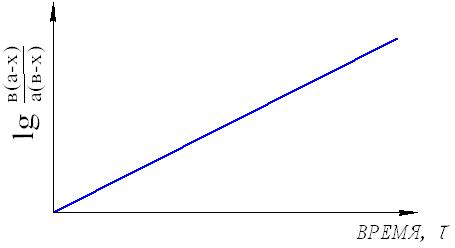 Рис.9. Значение lg(b(ax)/a(bx)) как функция времени для общего случая реакции второго порядка Для обратимых, сложных реакций кинетические уравнения имеют более сложный вид и рассматриваются в курсе физической химии. 1.3.3. Влияние температуры на скорость реакции Согласно молекулярно-кинетической теории, число соударений молекул пропорционально Зависимость скорости реакции от температуры приближённо описывается эмпирическим законом Вант-Гоффа: при повышении температуры на каждые 10 градусов скорость большинства химических реакций возрастает в 2- -4 раза. Математическое выражение этой закономерности: vt = v0 n или kt = k0 n где v0 (или k0) – скорость реакции при температуре to; vt (или kt) – скорость реакции при температуре t1; γ – температурный коэффициент скорости реакции; Температурный коэффициент показывает, как увеличится скорость реакции при повышении температуры на 10 градусов; он имеет свое значение для каждой конкретной реакции, т. к. зависит от природы реагирующих веществ. Определив экспериментально величину γ (или воспользовавшись справочными данными) можно приближённо рассчитать значение скорости при любой температуре (в относительно небольшом температурном интервале). Более строго зависимость скорости от температуры описывается уравнением Аррениуса (см. п.1.3.4). Большое влияние температуры на скорость реакций находит своё объяснение в теории активации. С ростом температуры средняя энергия молекул системы возрастает. На рис.10 кривые, относящиеся к температурам T2 и T3, смещены вправо – в сторону более высоких энергий по сравнению с кривой, относящейся к температуре Т1; соответственно, увеличивается и доля молекул, обладающих энергией, превышающей энергию активации реакции, следовательно, число активных молекул, а значит и эффективных столкновений, также увеличивается, поэтому скорость реакции растёт: v(T1) v(T2) v(T3) 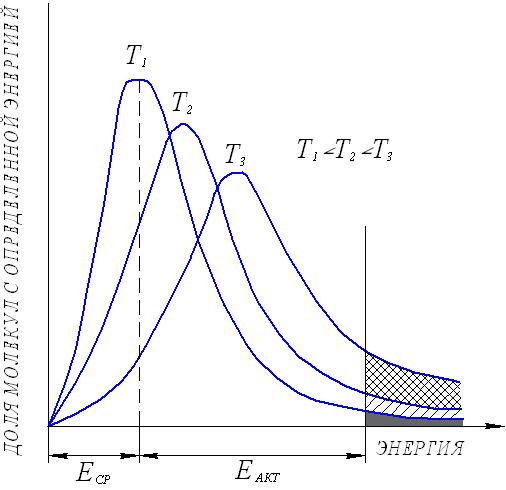 Рис.10. Распределение молекул по энергии при различных температурах: Еср-средняя энергия молекул; Еа-энергия активации; ∆N/(N∆E)-доля молекул с определенной энергией. 1.3.4. Уравнение Аррениуса Это уравнение, предложенное шведским учёным Аррениусом в 1889 году, выражает одновременно зависимость скорости реакции от энергии активации, температуры, а также энтропии активации реакции: Входящие в это уравнение величины k, Ea, T, R определены ранее. Величина H2 + I2 2HI 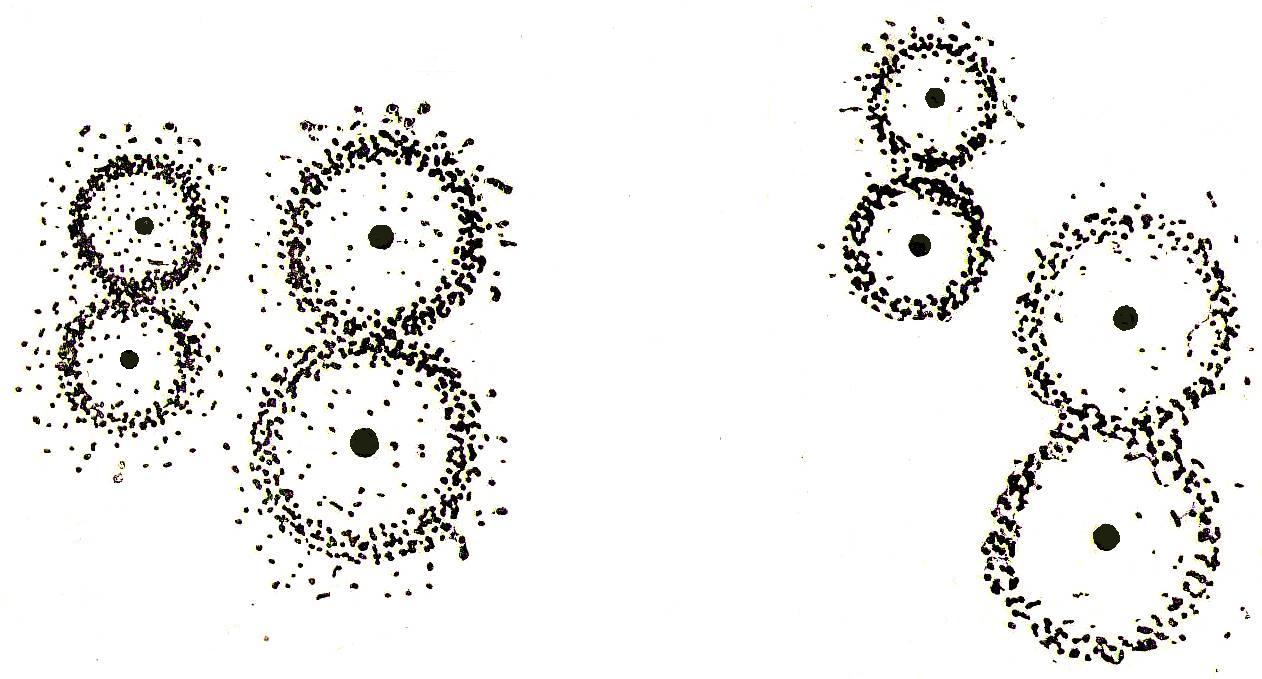 а) б) Рис 11. Благоприятные (а) и неблагоприятные (б) столкновения молекул H2 и I2 Другим примером роли стерического фактора может служить уменьшение скорости реакции этерификации (спирт + кислота сложный эфир + вода) при переходе от первичных спиртов к третичным. Третичные спирты (R3COH) имеют более сложное пространственное строение, чем первичные (RСН2–OH), поэтому возможность их благоприятной ориентации по отношению к молекулам кислоты менее вероятна. Величина ΔSa называется энтропией активации(Дж/моль·К), она пропорциональна отношению числа благоприятных способов ориентации к их общему возможному числу: 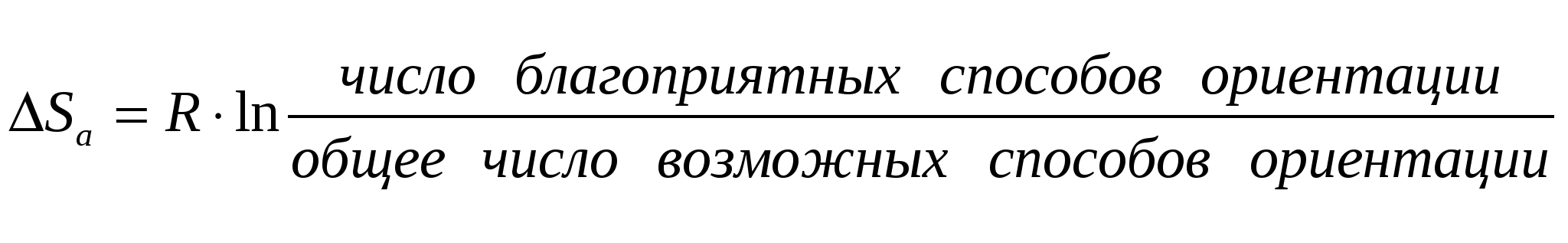 Отсюда очевидно, что чем жёстче требования ориентации, тем меньше будет величина ΔSa, а значит и скорость реакции. Значение стерического фактора особенно сказывается на реакциях с участием сложных молекул с разветвлённой структурой. Z – множитель, отражающий общее число столкновений взаимодействующих частиц. Произведение Определение энергии активации. Прологарифмировав уравнение Аррениуса, получим: Если построить график зависимости экспериментальных величин lgk от 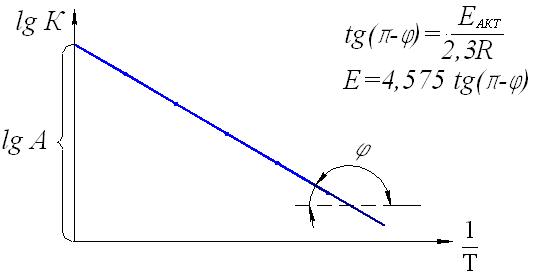 Рис.12. Графический расчет энергии активации Следовательно, для определения энергии активации необходимо иметь опытные данные по значениям константы скорости при нескольких температурах. Их представляют в виде таблицы:
и строят график зависимости Если известны только два значения константы скорости k1 и k2 при Т1 и Т2 соответственно, то уравнение (1.22) для этого случая запишется следующим образом: Вычитая уравнение (1.24) из (1.23), получим: или Еа = 2,3RT1T2.lg(k2/k1)/(T2T1) (1.25) Уравнение Аррениуса, таким образом, математически выражает важнейшие положения, вытекающие из теории активных столкновений:
1.3.5. Влияние среды на скорость реакции При химических реакциях в растворах большое влияние на её скорость оказывает природа растворителя. Последний не может рассматриваться только как инертная среда: во многих случаях растворитель играет роль активного участника реакции. Часто растворитель оказывает каталитическое воздействие на протекающий в растворе химический процесс. Скорость протекания одной и той же реакции может изменяться в широких пределах в зависимости от его природы. Например, тринитробензойная кислота С6H2(NO2)3COOH при 60оС разлагается в воде в 2050 раз, а в нитробензоле в 4000 быстрее, чем в толуоле при той же температуре. Можно привести множество других примеров. Очень большое значение имеют и возможные водородные связи между молекулами растворителя и растворенного вещества. Их влияние на скорость реакции в различных случаях различно. В водных растворах большое значение имеет характер среды (кислая, щелочная, нейтральная). Если реакция протекает в газовой фазе, то скорость химического процесса может быть замедлена введением в систему инертных газов (аргон, гелий, азот и др.) Роль среды настолько существенна, что нередко она предопределяет саму возможность (невозможность) протекания реакции. Закономерности влияния растворителя на скорость химического процесса определяются прежде всего энергией сольватации (взаимодействие частиц растворенного вещества с молекулами растворителя) и диэлектрической проницаемостью (величина, характеризующая полярность) растворителя. Рассмотрим примеры воздействия этих факторов: 1) хорошо известная реакция образования кристаллического хлорида серебра Ag+ + Cl AgCl практически мгновенно протекает в водном растворе и не идет в жидком аммиаке. Причина в том, что ионы серебра и хлора в растворе находятся в сольватированном ( в случае воды гидратированном) состоянии, и энергетические характеристики процессов Ag(H2O)4+ + Cl(H2O)2 = AgCl + 6H2O Ag(NH3)4+ + Cl(NH3) = AgCl + 5NH3 совершенно различны. В первом случае в результате разрыва связей ионов с молекулами воды (эндотермический процесс) и образования связи Ag Cl (экзотермический процесс) достигается энергетический выигрыш, и реакция идет, а во втором прочность связей иона серебра с молекулами аммиака настолько велика, что энергия, необходимая для ее разрыва, не компенсируется количеством энергии, которая могла бы выделиться при образовании молекулы хлорида серебра, то есть в этом случае процесс является энергетически невыгодным, и реакция не идет. По аналогичной причине ионы натрия и хлора в воде не взаимодействуют, а в жидком аммиаке выпадает осадок хлорида натрия: Na+ + Cl NaCl 2) многочисленными примерами можно проиллюстрировать влияние полярности растворителя; так, гидролиз третичного бутилхлорида: (CH3)3CCl + H2O (CH3)3COH + HCl значительно ускоряется при повышении полярности растворителей (в скобках значения диэлектрической проницаемости при 250С): в метиловом спирте (32,6) скорость выше, чем в этиловом спирте (24,3) в 9 раз, а в формамиде (109,5) в 430 раз. Еще существеннее влияние полярности растворителя на скорость реакции гидролиза триметилсульфония; так, при замене этилового спирта (24,3) на воду (CH3)3S+ + OH CH3OH + (CH3)2S (78,35) скорость падает в 20000 раз; 3) стоит также отметить влияние природы растворителя на мономер-димерное (полимерное) равновесие в растворах, что в свою очередь существенно сказывается на скорости реакций. Например, уксусная кислота склонна к димеризации, а по химическим свойствам молекулы CH3COOH и (CH3COOH)2 заметно отличаются друг от друга, т.к. в димере наиболее реакционноспособная часть молекулы гидроксильный водород участвует в образовании водородной связи, (той самой, за счет которой и образуется димер) и заметно теряет свою активность. Отсюда становится очевидным, что реакционная способность уксусной кислоты, находящейся в растворе в мономерной форме, должна быть значительно выше, чем у димерной формы этого соединения. Соотношение мономеров и димеров можно изменять подбором растворителя. Так, в растворе уксусной кислоты (0,1М) в циклогексане (неполярный растворитель) в мономерной форме будет находиться около 50% молекул, а в нитробензоле (полярный растворитель) 70%, и поэтому в нем она (как и фенол, спирты) проявляет более высокую реакционную способность. Как уже было показано выше, при протекании элементарного химического процесса в растворе частицы окружающей среды молекулы растворителя в какой-то степени обязательно в нем участвуют, и поэтому величина константы скорости реакции в той или иной мере зависит от того, в каком растворителе протекает рассматриваемая элементарная реакция. Значительного влияния среды на величину константы скорости следует ожидать в реакциях, в которых образование активированного комплекса сопровождается перестройкой сольватных оболочек исходных частиц. Это является результатом межмолекулярного взаимодействия исходных частиц и активированного комплекса с молекулами окружающей среды. В зависимости от характера разрыва связей в молекулах исходных веществ различают гомолитические и гетеролитические реакции. Гомолитическими называются реакции, в которых у каждого из атомов в результате разрыва связи остается по одному неспаренному электрону А В А+ В, а гетеролитическими реакции, в которых при разрыве связи оба электрона остаются у одного из атомов А В А: В. Влияние среды на скорость гомо- и гетеролитических реакций сильно различается. В гомолитических реакциях образование активированного комплекса может быть не сопряжено с существенным перераспределением электронной плотности между реагирующими атомами. Поэтому оно не должно сопровождаться сильными изменениями межмолекулярного взаимодействия, то есть происходит без существенных изменений в окружающей среде. В связи с этим можно ожидать, что переход реакции из газовой фазы в раствор или замена растворителя не должны существенно сказываться на величине константы скорости гомолитической реакции. В таблице 1 приведены величины констант скорости некоторых гомолитических реакций в газовой фазе и в различных растворителях. Видно, что значение константы скорости каждой реакции слабо зависит от природы растворителя и лежит в пределах одного порядка. Таблица 2 Константы скорости некоторых гомолитических реакций в некоторых средах
В гетеролитических реакциях, в противоположность гомолитическим, электронная плотность существенно перераспределяется между реагирующими частицами, поэтому их сольватные оболочки должны претерпевать существенную перестройку. Поэтому, в гетеролитических реакциях следует ожидать сильного влияния среды на скорость реакции. Примером может служить реакция CH3I + Cl, относительная скорость которой изменяется, в зависимости от растворителя, в пределах семи порядков: растворитель CH3OH HCONHCH3 HCON(CH3)2 CH3CON(CH3)2 относительная константа скорости 1 45,3 1,2 106 7,4 106. |
