контра. 1. Выбор задач и варианта Студент должен выбрать для своей контрольной работы задачу С1 и по одной (любой) задаче из разделов Кинематика
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
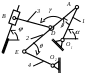
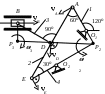
Образец выполненияУсловия задачи. Плоский механизм состоит из стержней 1–4 и ползуна B ; O1 и O2 неподвижные шарнирные опоры (рис.8а). Длины стержней: l1 = 0,4 м, l2 = 1,2 м, l3 = 1,4 м, l4 = 0,8 м. Положение механизма определяется углами = 120, = 60, = 90, = 0, = 30. Известна угловая скорость стержня 1: 1 = 5 с-1. Определить скорости vB, vE, 3. Решение. Изображаем положение механизма в соответствии с заданными углами (рис.8б). Из условий задачи ясно, что стержень 1 вращается с угловой скоростью 1 = 5 с-1вокруг неподвижной оси, проходящей через точку O1 . Следовательно, модуль вектора vA скорости точки А находится по известной формуле vA = 1 ·AO1 = 1·l1 = 5с-1· 0,4м = 2 м/с , а направление vA перпендикулярно AO1 .
Рис. 8 Определим теперь vE - скорость точки Е, которая принадлежит стержню 2. Для её нахождения достаточно знать скорость какой-либо другой точки стержня 2 , например vA , и направление вектора vE. Заметим, что точка E принадлежит стержню O2Е, который вращается вокруг неподвижной оси, проходящей через точку O2 , следовательно, vE EO2. Для нахождения величины vE используем теорему о равенстве проекций скоростей точек А и Е твердого тела (стержня 2) на отрезок АЕ , который их соединяет [1, c.131]: Предварительно установим, в какую сторону направлен вектор vE . Проекции скоростей vA и vE на отрезок АЕ должны иметь одинаковые знаки, следовательно вектор vE направлен вниз, и звено 4 вращается против хода часовой стрелки (рис.8б). Из равенства проекций (1) получим : vA cos 30 = vE cos 60 , откуда vE = vA cos 30/ cos 60 = 2м/с·0,863/0,5 = 3,4 м/с. Точка B принадлежит стержню BD. Для определения vB сначала найдем скорость точки D, являющейся общей для cтержней 2 и 3. Величину скорости vD найдем, построив мгновенный центр скоростей (МЦС) звена AE – точку P2, лежащую на пересечении перпендикуляров к векторам vA и vE, восстановленных из точек A и E. Заметим, что векторы vA и vE перпендикулярны стержням 1 и 4, следовательно точка P2 лежит на пересечении прямых AO1 и EO2 (рис.8б). По направлению вектора vA определяем направление угловой скорости 2 вращения звена AE вокруг МЦС P2. Вектор vD перпендикулярен отрезку P2D и направлен в сторону вращения AE вокруг P2 (рис.8б). Величину vD можно найти из пропорции [1, c.133] : vD / P2D = vA /P2A. (2) Заметим, что AP2E – прямоугольный с углами при вершинах A и E соответственно 30 и 60, следовательно P2 A = AE·sin 30 = AD. Тогда AP2D является равносторонним (P2A = P2D) и согласно пропорции (2) vD = vA = 2 м/с . Точка B звена BD принадлежит также и ползуну B, движущемуся поступательно вдоль горизонтальных направляющих. Следовательно, направление vB известно. Восстанавливаем из точек B и D перпендикуляры к скоростям vB и vD и находим точку их пересечения P3 - МЦС звена BD. По направлению вектора vD определяем направление угловой скорости 3 вращения стержня BD вокруг P3. Вектор vB также направлен в сторону вращения BD вокруг P3 (рис.8б). Величины угловой скорости звена 3 и скорости точки B найдем, используя свойства МЦС [1, c.133] 3 = vD / P3D = vD / (l3 cos 30) = 1,6 с-1 , vB = 3 ·P3B = 3 (l3 sin 30) = 1,1 м/с. Ответ: vB = 1,1 м/с ,vE = 3,5 м/с , 3 = 1,6 с-1. |