Главная страница
Навигация по странице:

  • Задача Д1 Груз D массой m , получив в положении А начальную скорость V

    		•

    контра. 1. Выбор задач и варианта Студент должен выбрать для своей контрольной работы задачу С1 и по одной (любой) задаче из разделов Кинематика


    Скачать 1.01 Mb.
    Название1. Выбор задач и варианта Студент должен выбрать для своей контрольной работы задачу С1 и по одной (любой) задаче из разделов Кинематика
    Анкорконтра
    Дата09.11.2020
    Размер1.01 Mb.
    Формат файлаdoc
    Имя файлаKontr_rabota.doc
    ТипКонтрольная работа
    #149209
    страница6 из 8
    1   2   3   4   5   6   7   8

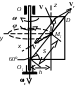
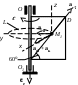
    Образец выполнения



    Условия задачи. Прямоугольная пластина (рис.9а) вращается вокруг оси O1O согласно уравнению = – 4 t2 (рад); положительное направление отсчета угла указано на рис.9а дуговой стрелкой. Точка M совершает относительное перемещение вдоль отрезка AD по законуAM= s = 60 (t2 – t) + 20 см .

    Определить абсолютную скорость vа и абсолютное ускорение aа точки M в момент времени t1 = 1 с.

    Решение. Рассмотрим движение точки M как сложное, состоящее из относительного движения точки вдоль диагонали AD пластины и пе-

    Р
    ис. 9а
    Р
    ис.9б

    реносного вращения вместе с самой пластиной.

    Установим положение точки М на диагонали AD в момент времени t1 = 1с.

    Относительное движение точки М происходит по закону

    s = 60 (t2 – t) + 20 .

    Полагая здесь t = 1 с, получим s = 20 см. Изображаем соответствующее положение точкой M1 на рис. К9а ( АM1 = 20 см ) .

    Определяем кинематические характеристики относительного и переносного движений.

    Находим векторы относительной скорости vr и ускорения ar. Дифференцируя зависимость s(t) по времени, находим выражение для значения относительной скорости

    , (2)

    откуда для момента времени t1 = 1c получаем vr = 60 см/с.

    Поскольку траекторией относительного движения является прямая, то величина относительного ускорения точки М выражается второй производной от s по времени

    см/с2 . (3)

    Положительные значения производных (3), (4) указывают, что векторы vr и ar направлены в сторону положительного отсчета дуговой координаты s. Изображаем эти векторы на рис.9а и 9б, приложенными к точке M1.

    Находим векторы переносной скорости ve и ускорения ae. Уравнение переносного вращения пластины: = – 4 t2 (рад). Положительное направление отсчета угла указано на рис.9а дуговой стрелкой c буквой .

    Дифференцируя зависимость (t) по времени, найдем выражения для переносной угловой скорости

    (с-1) (4)

    и переносного углового ускорения

    с-2 . (5)

    Для момента времени t = 1с из выражения (4) имеем e = – 8 с-2 . Отрицательное значение производной (4) указывает, что направление вращения пластины противоположно положительному направлению отсчета угла .; покажем направление вращения пластины на рис.9а дуговой стрелкой с буквой е. Вектор переносной угловой скорости e направлен вдоль оси вращения ОО1 пластины так, что с его конца вращение наблюдается происходящим против хода часовой стрелки. Изобразим вектор e на рис.9а.

    Знаки при e и e одинаковы (оба отрицательны), а следовательно, вращение пластины является ускоренным. Изображаем это дуговой стрелкой e на рис.К9б.

    Переносные скорость и ускорение точки М в момент времени t1 - это скорость и ускорение точки М1 пластины. При вращении пластины её точка М1 описывает окружность радиуса h = AM1 sin 30 = 10 см. Тогда модуль вектора переносной скорости

    , (6)

    а вектор переносного ускорения складывается из касательной ae и нормальной aen составляющих

    , (7)

    модули которых определяются по формулам

    , . (8)

    Изображаем векторы ve, ae, aen приложенными в точке M1 на рис.9а и 9б. Векторы ve, ae направлены по касательной к траектории точки М1 (окружности L) в сторону вращения пластины; вектор aen направлен вдоль радиуса окружности L к оси вращения O1O.

    Находим вектор ускорения Кориолиса aк , используя известную формулу [1, с.162]:

    a к = 2 e × vr

    Модуль этого векторного произведения , где

    угол между векторами относительной скорости vr и переносной угловой скорости e составляет 150 (см. рис.9б). С учетом (2) и (4) для момента времени t1 = 1 с получаем:

    aк = 2·8·60·sin 150 = 480 см/с2. (9)

    Направление a к удобно находить по правилу Жуковского. Проектируем вектор vr на плоскость переносного вращения (плоскость окружности L). Затем поворачиваем полученную проекцию, направленную противоположно вектору a еn, на 90 в сторону переносного вращения (в данном случае - по ходу часовой стрелки). В результате установим, что направления векторов a к и a е совпадают (рис.9, б).

    Находим абсолютную скорость и абсолютное ускорение точки M, используя теоремы сложения (1).

    При нахождении модуля абсолютной скорости учитываем перпендикулярность векторов vr и ve (рис.9а). Для момента времени t1 = 1с с учетом (2) и (6) получаем

    = 100 см/с = 1 м/с .

    Теорема о сложении ускорений (1) с учетом равенства (7) принимает вид

    a а = a r + a e + a en + aк (10)

    Для нахождения суммы четырех векторов в правой части (10) используем метод проекций. Вычислим координаты вектора a а в системе М1xyz , изображенной на рис.9б. Для этого спроектируем на координатные оси обе части векторного равенства (10), учитывая, что направления и модули векторов a r , ae , aen , a к уже известны:

    aах = ae + aк = 80 + 480 = 560 см/с2,
    aаy = aen – ar cos 60 = 640 –120·0,5 = 700 см/с2,
    aaz = ar cos 30 = 120·0,86 см/с2 = 103 см/с2 .

    После этого модуль абсолютного ускорения находим по известной формуле векторной алгебры [2, c.226] :

    902см /с2 ≈ 9 м/с2.

    Ответ: va = 1 м/с , aa = 9 м/с2.

    ДИНАМИКА
    Общими для условий всех задач являются допущения :

    - все нити (тросы) - абсолютно гибкие нерастяжимые и невесомые;

    - скольжение нитей, перекинутых через блоки отсутствует;

    - качение катков (колес) происходит без проскальзывания.

    Номер

    условия
    m кг
    V0 м/с
    Q H
    R

    H
    АВ м
     с
    Fx (t)

    Н

    0
    2,4
    12
    5
    0,8V 2
    1,5
    -
    4 sin(4t)

    1
    2
    20
    6
    0,4V 2
    -
    2,5
    - 5 cos(4t)

    2
    8
    10
    16
    0,5V 2
    4
    -
    6t 2

    3
    1,8
    24
    5
    0,3V 2
    -
    2
    - 2 cos(2t)

    4
    6
    15
    12
    0,6V 2
    5
    -
    - 5 sin(2t)

    5
    4,5
    22
    9
    0,5V
    -
    3
    3t

    6
    4
    12
    10
    0,8V 2
    2,5
    -
    6 cos(4t)

    7
    1,6
    18
    4
    0,4V
    -
    2
    - 3 sin(4t)

    8
    4,8
    10
    10
    0,2V 2
    4
    -
    4 cos(2t)

    9
    3
    22
    9
    0,5V
    -
    3
    4 sin(2t)
    Задача Д1
    Груз D массой m, получив в положении А начальную скорость V0 , движется по изогнутой трубке ABC, расположенной в вертикальной плоскости (рис. Д1.0 - Д1.9). На прямолинейном участке АВ на груз кроме силы тяжести действуют:

    - постоянная сила Q (ее направление показано на рисунках, а модуль даётся в таблице 1.);

    - сила сопротивления R , направленная противоположно скорости V груза (выражение для модуля силы R дано в табл.1.).

    Расстояние АВ = Lили время движения груза из положения А в положение В считаются известными и даются в табл. 1.
    Таблица 1
    В точке В груз, не изменяя значение своей скорости, переходит на прямолинейный участок ВС трубки. Здесь действие сил Q и R прекра-щается, и на груз кроме силы тяжести, действуют:

    - параллельная оси трубки переменная сила F(t), проекция которой Fx(t) задана в табл.1 (ось х - направлена вдоль ВС от В к С);

    - сила кулоновского трения о стенки трубки (коэффициент трения f= 0,2 ).

    Считая груз материальной точкой, найти закон движения груза на участке ВС, т.е. зависимость , где x = BD.

    Указания. Д1 - задача на интегрирование дифференциального уравнения прямолинейного движения материальной точки [1], с.189.

    Решение задачи состоит из двух частей:

    1. Сначала нужно составить и проинтегрировать дифференциальное уравнение движения точки (груза) на участке АВ. В результате, зная время движения на участке АВ или его длину L , можно определить скорость груза в точке В (эта скорость будет начальной для движения на втором участке – ВС).

    В случае, когда задана длина L участка АВ, целесообразно исключить время t из дифференциального уравнения движения с помощью следующего преобразования

    (1)

    где z – обозначение координатной оси, направленной вдоль АВ .

    2. Затем следует составить и проинтегрировать дифференциальное уравнение движения груза на участке ВС, ведя отсчет времени от мо-мента , когда груз находится в точке В (положите в этот момент t = 0).

    На участке ВС учитывается сила трения, направление которой противоположно скорости тела. Если при движении вдоль ВС тело остановится (или изменит направление движения), то следует определить момент времени, когда это впервые произойдет.
    Образец выполнения задачи Д1

    Условия задачи. Участок АВ длиной L = 2,5 м расположен вертикально, а участок ВС - под углом 30 0 к горизонту (рис.1).

    Масса груза m = 2 кг; в положении А его скорость V0 = 5 м/с . Модуль силы сопротивления Н ( - скорость груза в м/с). Проекция силы F на ось Вх задана выражением Н (t– в с). На участке ВС коэффициент трения груза о стенки трубки f= 0,7.

    Определить закон движения груза на участке ВС : x = f(t).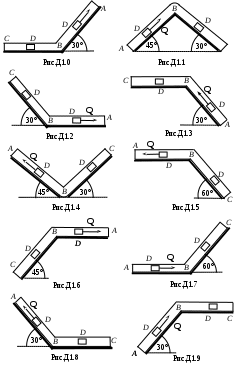


    Решение. Изобразим груз в его произвольном положении на участке АВ и все действующие на него силы: силу тяжести P = mg и силу сопротивления R (рис.1).

    Считая груз материальной точкой, запишем для него основной закон динамики:

    (2)

    Проектируя векторное уравнение (1) на ось Az с началом в точке А (рис.1) , получаем дифференциальное уравнение движения груза

    ,

    которое с учетом преобразования (1) и направлений действующих сил, показанных на рис.1, принимает вид:

    y1, y2


    A


    9

    R


    y1(t)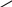



    D



    6



    1   2   3   4   5   6   7   8

    написать администратору сайта