контра. 1. Выбор задач и варианта Студент должен выбрать для своей контрольной работы задачу С1 и по одной (любой) задаче из разделов Кинематика

• Название: 1. Выбор задач и варианта Студент должен выбрать для своей контрольной работы задачу С1 и по одной (любой) задаче из разделов Кинематика
• Анкор: контра
• Дата: 09.11.2020
• Размер: 1.01 Mb.
• Имя файла: Kontr_rabota.doc
• Тип: Контрольная работа; #149209
• страница: 1 из 8

Задачи контрольной работы по теоретической механике для

студентов специальности ТЛДП(б) заочной формы обучения
1. Выбор задач и варианта

Студент должен выбрать для своей контрольной работы задачу С1 и по одной (любой) задаче из разделов «Кинематика» и «Динамика».

К каждой из задач даются 10 рисунков и таблица, содержащая дополнительные к тексту задачи условия. Нумерация рисунков двойная, при этом номером рисунка является цифра, стоящая после точки. Например, рис.С1.4 - это рис.4 к задаче С1. Номер условия от 0 до 9 проставлен в 1-м столбце каждой таблицы.

Студент в каждой задаче выбирает номер рисунка по первой цифре шифра, а номер условия в таблице - по второй цифре шифра. Например, шифру 06, соответствует рисунок с номером 0 и условия из строки таблицы с номером 6 . Шифр выдается индивидуально каждому студенту преподавателем.

Следует иметь в виду, что некоторые из заданных в условиях задачи величин при решении некоторых вариантов могут не понадобиться. Поэтому из всех пояснений в условиях задачи обращайте внимание только на те, которые относятся к вашему варианту.
2. Правила оформления
Контрольная работа выполняется в тетради (объемом 12-24 листа). На обложке указывают название дисциплины, номер работы, фамилия и инициалы студента, шифр (номер зачетной книжки), факультет, специальность. На первой странице тетради записываются номер контрольной работы и номера решаемых задач,

На каждой странице должны быть оставлены поля размером 3 см для замечаний рецензента.

Запись решения каждой задачи следует начинать на четной странице, начиная со второй. Обязательно укажите номер решаемой задачи, кратко изложите условия (не переписывая текст условий дословно) и вопрос задачи, сделайте рисунок (желательно карандашом).

Рисунок выполняется с учетом условий решаемого варианта задачи; углы, действующие силы, число тел и их расположение на рисунке, должны соответствовать этим условиям. Рисунок должен быть аккуратным. Он должен наглядно показывать направления векторов (сил, скоростей, ускорений и пр.), а также расположение используемых в решении координатных осей.

Решение задач необходимо сопровождать краткими пояснениями:

- какие теоремы или формулы применяются;

- в результате каких операций или преобразований получаются те или иные результаты;

Следует также указывать названия всех физических величин, вычисляемых по ходу решения задачи.

В решении должен быть представлен полностью ход числовых расчетов.

Указание размерностей исходных (заданных) и получаемых величин обязательно.

В конце решения задачи должен быть сформулирован ответ.

Методические указания по решению задач, входящих в контрольные работы, даются для каждой задачи после изложения ее текста под рубрикой "Пример решения задачи". Назначение примера – не только разъяснить ход решения, но и продемонстрировать правильный стиль его оформления.

3. ПРОВЕРКА И РЕЦЕНЗИРОВАНИЕ КОНТРОЛЬНЫХ РАБОТ
Контрольные работы, не отвечающие требованиям, перечисленным в п.2, не проверяются и возвращаются для переоформления.

К работе, высылаемой на повторную проверку (если она выполнена в другой тетради), должна обязательно прилагаться незачтенная работа.

На экзамене (зачете) необходимо представить зачтенные контрольные работы по соответствующему разделу курса, в которых все отмеченные рецензентом погрешности должны быть исправлены.

Срок рецензирования одной контрольной работы преподавателем – не более 7 дней.
4. ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ РАБОТ
Для обозначения векторных величин далее повсюду используется прямой шрифт с выделением, например F, a, v ; а для скалярных – курсив без выделения, например M, F_x , v,  .
Задача С1
Жесткая рама (рис.С1.0 – С1.9) закреплена неподвижно на двух опорах А и В. Опора А – неподвижный цилиндрический шарнир. Опора В – или подвижный шарнир (рис.С1.0 - С1.2, С1.5, С1.8) или невесомый стержень BО, который крепится к раме и к неподвижному основанию О шарнирами (рис.С1.3, С1.4, С1.6, С1.7, С1.9)

На раму действуют:

- пара сил с моментом М, величина которого указана в табл.1, а направление на рисунке;

- сосредоточенные силы F₁ , F₂ , F₃ , F₄ , которые имеют вели­чины, направления и точки приложения, указанные в табл.1 (напри­мер, в условии 1 сила F₁ имеет величину F₁ = 10 кН, направлена под углом 30° к го­ризонтальной оси и приложена в точке К рамы).

- равномерно распределенная cила, интенсивность которой q = 2 кН/м, а участок приложения показан на рисунке.

Определить реакции опор А и В.

При окончательных подсчетах принять а = 0,6 м.

Указания. С1 – задача на составление уравнений равновесия для тела, находящегося под действием плоской системы сил. Эти уравнения выражают необходимые и достаточные условия равновесия свободного твердого тела и имеют вид [1, с.46] :

, , . (1)

Для составления уравнений (1) предварительно требуется:

- заменить распределенную силу ее равнодействующей;

- освободить тело от наложенных на него связей, заменив их реакциями (силами);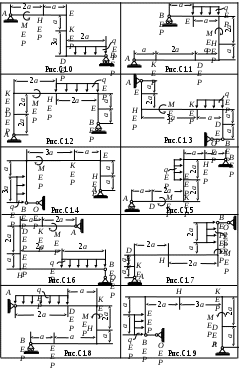





Таблица 1.

Сила									Момент пары , кНм
Номер условия	F1= 10 кН		F2= 20 кН		F3= 30 кН		F4­= 40 кН
	Точка прилож.	1, град.	Точка прилож.	2, град.	Точка прилож.	3, град.	Точка прилож.	4, град.
0 1 2 3 4 5 6 7 8 9	– K – D – H – D – E	– 30 – 60 – 60 – 45 – 30	D – H – K – E – H –	60 – 45 – 30 – 30 – 60 –	E – K – E D – H – –	45 – 30 – 60 30 – 60 – –	– H – E – – K – D K	45 – 30 – – 60 – 30 60	10 14 20 26 12 24 30 22 18 38

- выбрать направления осей x и y для проектирования и моментную точку О.

В качестве моментной рекомендуется выбирать точку, в которой пересекаются линии действия двух реакций. В этом случае уравнение моментов будет содержать лишь одну неизвестную реакцию.

При вычислении момента силы F_i ( i = 1, …, 4) удобно разложить её на составляющие F_i^', F_i^'' , для каждой из которых плечо легко вычисляется, а затем воспользоваться теоремой Вариньона (о моменте равнодействующей) [1, c.40]:

(2)
Образец выполнения
Условия задачи. Жесткая рама ADEB закреплена на двух опорах: A (подвижный шарнир) и B (неподвижный шарнир). На раму действуют заданные активные силы:

• 
  сосредоточенная сила F величиной 25 кH, приложенная в точке D;
  
• 
  пара сил с моментом М = 50 кН·м (направление момента показано на рис.1 дуговой стрелкой);
  
• 
  равномерно распределенная на участке EВ сила интенсивностью
  

q = 2 кН/м.

Размеры и углы показаны на рис1; а = 0,5 м .

Определить реакции опор А и В .

Решение. Рассмотрим равновесие рамы АDEВ. Изобразим на рисунке действующие на раму активные силы. Равномерно распределенную на участке ЕВ силу заменим её равнодействующей Q , величина которой

Q = q · ЕВ = q · 2а = 20 кН/м · 1м = 20 кН ,

а линия действия проходит через середину участка ЕВ (рис.1).

О 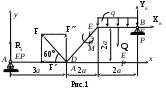свободим раму от связей, наложенных в точках А и В , заменив эти связи силами - реакциями. Реакцию неподвижного шарнира R_В, направление которой неизвестно, разложим на две составляющие: горизонтальную - X_В и вертикальную - Y_В . Реакция R_А подвижного шарнира А (шарнира на катках) направляется перпендикулярно опорной плоскости катков – вертикально.

Для составления уравнений равновесия (1) введем координатные оси ху ­и выберем в качестве моментной точку В, через которую проходят линии действия двух неизвестных реакций X_В и Y_В .

Записываем уравнения проекций сил на оси x и y :

, , (2)

, . (3)

Действующая на раму пара сил в уравнениях проекций не учитывается, поскольку сумма проекций сил пары на любую ось равна нулю.

Записываем уравнение моментов:

, . (4)

Здесь для вычисления момента силы F относительно точки В использовалась теорема Вариньона (2). Сила F была разложена на две составляющие: F = F^' + F^'' (рис.1), величины которых , . После этого момент силы F был найден как сумма моментов этих составляющих:





Подставляем в составленные уравнения равновесия (2), (3), (4) числовые значения заданных величин:

; ;

. (5)

Решая систему линейных уравнений (5), находим числовые значения искомых реакций.

Ответ: R_А = 1,4 кН , Х_В = 12,5 кН , Y_В = – 2,7 кН (отрицательный знак указывает, что сила Y_В имеет направление, противоположное изображенному на рис.1)
Задача С2
Однородная прямоугольная плита весом Р = 3 кН со сторонами АВ = 3a, ВС = 2а неподвижно закреплена на трёх опорах (рис. С2.0-С2.9): в точке А - сферическим шарниром; в точке В - цилиндрическим шарниром (шарнирной петлей); в точке С опирается на невесомый стержень СО.

На плиту действуют: пара сил с моментом М = 5 кНּм, лежащая в плоскости плиты; сосредоточенные силы F₁ , F₂ , F₃ , F₄ , величины, направления и точки приложения которых указаны в табл. 2.

Определить реакции опор А, В и С. При окончательных подсчетах принять а = 0,8 м.

Указания. Задача С2 – на составление уравнений равновесия для тела, находящегося под действием пространственной системы сил [1, c.79] :
, , ,
, , . (1)


КИНЕМАТИКА
Задача К1

По заданным в декартовых координатах в табл.4 уравнениям движения точки x = x(t) , y = y(t) найти вид её траектории.

Для заданного момента времени t₁ =1с определить :

- положение точки на траектории;

- скорость и ускорение точки;

- её касательное и нормальное ускорения;

- радиус кривизны в соответствующей точке траектории.

Таблица 4

П е р в а я ц и ф р а ш и ф р а
	0	x = 4sin(t ⁄6)	3	x = 4 − 2t	7	x = 12 cos(t ⁄6)
	1	x = 3 − 6sin(t ⁄6)	4	x = 2t + 4	8	x = 6cos(t ⁄6) − 2
	2	x = 3sin(t ⁄6) − 2	5	x = − 2t	9	x = 4 − 8cos(t ⁄6)
			6	x = 2t+ 2
Вторая цифра шифра	0	y = 4 − 9 cos(t ⁄6)	y = t 2− 2		y = − 4 cos(t ⁄3)
	1	y = 2 − 3 cos(t ⁄3)	y = 8 cos(t ⁄4)		y = 10 sin(t ⁄6)
	2	y = 4 − 6 cos2(t ⁄6)	y = 4 + 2 t 2		y = 12 sin2(t ⁄6)
	3	y = 12 cos(t ⁄6)	y = 2 (t +1) 2		y = 2 − 4 sin(t ⁄6)
	4	y = 9 cos(t ⁄3) + 5	y = 2 + 2 sin(t ⁄4)		y = 8 + 12 sin(t ⁄3)
	5	y = − 10 cos(t ⁄6)	y = 3 t 2− 2		y = 3 sin(t ⁄6)
	6	y = 8 cos(t ⁄6) − 3	y = 3 − 4 cos(t ⁄4)		y = 6 sin2(t ⁄6) − 7
	7	y = − 9 cos2(t ⁄6)	y = 3 − 4cos(t ⁄4)		y = 6 cos(t ⁄3)
	8	y = 6 cos(t ⁄3) − 4	y = 2 t 3		y = 4 − 9 sin(t ⁄6)
	9	y = 2 − 2 cos(t ⁄6)	y = 2 sin(t ⁄4)		y = 8 cos(t ⁄3) + 6

Указания. К1 – задача на определение кинематических характеристик движения точки [1, с.99-110] .

В задаче требуется по заданным уравнениям движения точки получить уравнение ее траектории в явной y = f(x) или в неявной F(x, y) = 0 форме. В некоторых вариантах задачи для этого следует использовать известные тригонометрические формулы: sin ²+ּcos ²= ;

cos 2= 1 – 2ּsin ²2ּcos ² ;sin 2= 2ּsinּcos

Изображение траектории необходимо построить на рисунке, предварительно выбрав масштаб. На траектории следует указать положение точки в момент времени t= t₁ , а также построить соответствующие этому моменту времени векторы : скорости v, полного a , касательного a_ и нормального a_n ускорений точки.