контра. 1. Выбор задач и варианта Студент должен выбрать для своей контрольной работы задачу С1 и по одной (любой) задаче из разделов Кинематика

• Название: 1. Выбор задач и варианта Студент должен выбрать для своей контрольной работы задачу С1 и по одной (любой) задаче из разделов Кинематика
• Анкор: контра
• Дата: 09.11.2020
• Размер: 1.01 Mb.
• Имя файла: Kontr_rabota.doc
• Тип: Контрольная работа; #149209
• страница: 7 из 8

P

y₁= y₂


3

N

B

y₂(t)

T

t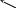

0

/2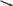



F

z

C

D

t₁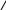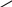

–3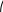

P

x

30°

Рис.1

Рис.2

(3)

Подчеркнём, что все переменные силы, входящие в дифференциальное уравнение движения надо обязательно выразить через величины от которых они зависят.

В дальнейшем проекцию V_z cкорости груза на ось Az будем для краткости обозначать V .

Подставляя в (3) числовые значения массы m груза, ускорения свободного падения g = 9,8 м/с² и разделяя переменные, получаем

или (4)

Проинтегрируем обе части (4) :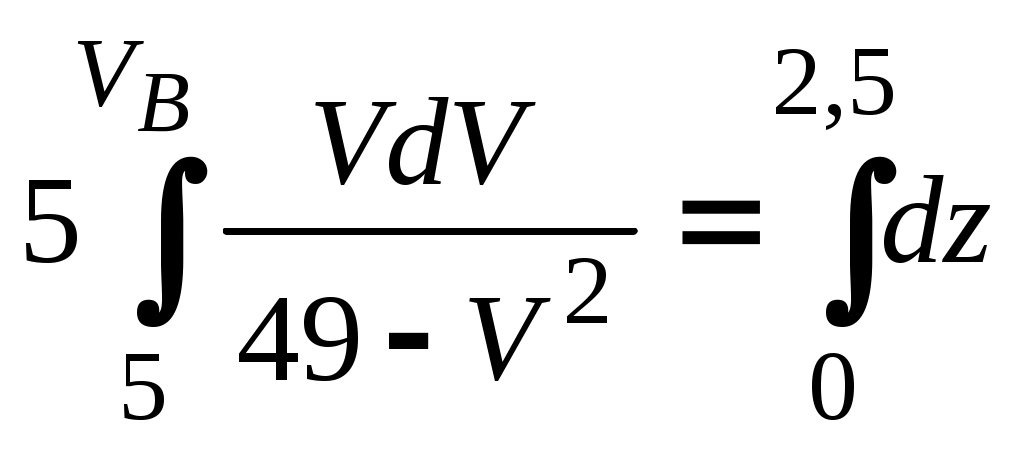

(5)

Здесь для установления пределов интегрирования используются начальные условия: при z = 0 (положение А) скорость груза V = V₀ =5м/с;

а также заданное значение для z_В = L = 2,5 м.

После вычисления интегралов в обеих частях уравнения (5) получим : или .

Потенцируя последнее равенство, находим и определяем скорость груза в положении В:

Перейдем к анализу движения груза на участке ВС. Скорость будет начальной скоростью движения на этом участке .

Изобразим груз в произвольном положении на ВС и укажем действующие на него силы: силу тяжести P = mg, нормальную реакцию стенок трубки N, силу трения о стенки T и заданную переменную силу F(t) (рис.1).

Согласно основному закону динамики для груза D на участке ВС :

(6)

Введем координатную ось Вx с началом в точке В . Спроектировав на неё (6) получим дифференциальное уравнение движения груза:

(7)

где проекции: ; ; ;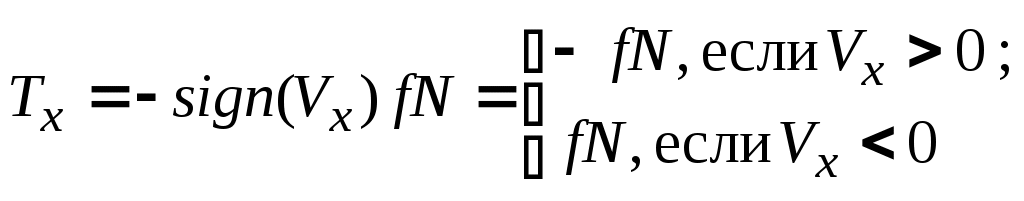

(8)

Последнее равенство означает, что изменение направления движения тела ( ) вызовет изменение направления силы трения: . В начале движения вдоль ВС , поэтому примем:



После подстановки значений проекций в (7) получаем:

(9)

Умножая обе части уравнения (9) на dt и интегрируя, найдем

(10)

Будем отсчитывать время от момента, когда груз находится в точке В, тогда при t = 0 : . Подставляя в равенство (10) значения t = 0, , получим :

При найденном значении уравнение (10) дает

(11)

Умножая в (11) обе части на dt и интегрируя, найдем

(12)

Так как при t = 0 груз находится в положении В, а значит x = 0, то из (12) следует . Искомый закон движения груза на участке ВС :

, (x – в метрах, t – в секундах) (13)

Уравнение (13) правильно описывает движение груза только до тех пор, пока его скорость . Поэтому следует определить момент времени, когда груз останавливается или меняет направление своего движения ( ). Это время находится из уравнения

или (14)

Приближенное решение уравнения (14) можно найти графическим способом. Для этого строим графики функций и (рис. 2). Абсцисса точки пересечения графиков функций y₁(t) и y₂(t) (рис.2) является корнем уравнения (14).

Итак в момент с груз останавливается ( ) в положении 18,9 м . Груз продолжит свое движение лишь тогда, когда силы , P преодолеют силу трения т.е. если

или

Последнее неравенство выполняется только при Н. Это значит, что груз будет продолжать движение вдоль ВС "рывками".

Задача Д2

Механическая система состоит двух ступенчатых шкивов 4 и 5 c радиусами ступеней R₄ = 0,3 м , r₄ = 0,1 м и R₅ = 0,2 м , r₅ = 0,1 м , грузов 1, 2 и катка 3, связанных гибкой нерастяжимой нитью.

Массы шкивов m₄,m₅ следует считать равномерно распределенными по их внешним ободам; каток 3 - сплошной однородный цилиндр

радиусом r₃ = 0,1 м .

Под действием силы F, модуль которой зависит от перемещения s точки её приложения (т.е. F = f (s)), система приходит в движение из состояния покоя.

При вращении шкивов 4 и 5 на них действуют пары сил сопротивления с постоянными моментами M₄ и M₅ соответственно. Коэффициент трения скольжения грузов 1, 2 о плоскость f = 0,1. Коэффициент трения качения катка 3 по плоскости  = 4 мм .

Определить значение искомой величины в тот момент времени, когда перемещение точки приложения силы F равно . Искомая величина указана в столбце «Найти» таблицы 2, где обозначено: _ - угловая скорость шкива 4, V₁ - скорость груза 1, V_C3 - скорость центра масс катка 3 и т.д.

Таблица 2

Номер усло-вия	m1кг	m2кг	m3кг	m4кг	m5кг	M4 Нм	M5 Нм	F = f(s) Н	 м	Най- ти
0	2	0	4	6	0	0	0,8	50(2+3s)	1,0	V1
1	6	0	2	0	8	0,6	0	20(5+2s)	1,2	
2	0	4	6	8	0	0	0,4	80(3+4s)	0,8	VC 3
3	0	2	4	0	10	0,3	0	40(4+5s)	0,6	V2
4	8	0	2	6	0	0	0,6	30(3+2s)	1,4	
5	8	0	4	0	6	0,9	0	40(3+5s)	1,6	V1
6	0	6	2	8	0	0	0,8	60(2+5s)	1,0	
7	0	4	6	0	10	0,6	0	30(8+3s)	0,8	
8	6	0	4	0	8	0,3	0	40(2+5s)	1,6	VC 3
9	0	4	6	10	0	0	0,4	50(3+2s)	1,4	V2

Указания. Д2 - задача на применение теоремы об изменении кинетической энергии механической системы [1], c.307.

(1)

При решении задачи следует учесть, что кинетическая энергия системы равна сумме кинетических энергий всех входящих в систему тел. Эту энергию надо выразить через ту скорость (линейную или угловую), которую требуется определить в задаче.

При вычислении кинетической энергии катящегося катка 3 для установления зависимости между его угловой скоростью ₃ и скоростью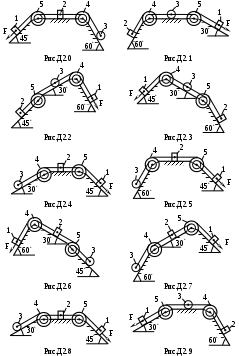



его центра масс V_C3 следует использовать мгновенный центр скоростей катка.

Рассматриваемая система является неизменяемой (тела - абсолютно твердые, нити – нерастяжимые), поэтому суммарная работа внутренних

сил равна нулю [1], с.308. Следовательно, в правой части (1) учитываются лишь работы внешних сил. Все перемещения, необходимые для вычисления работ, следует выражать через заданное перемещение .

Если по данным таблицы m₁ = 0 или m₂ = 0, то соответствующее тело можно на рисунке не изображать.
О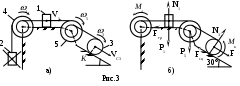
бразец выполнения задачи Д2

Условия задачи. Массы тел системы, изображенной на рис.3: m₁=4 кг, m₂ = 0 (поэтому тело 2 на рис.3б не показано), m₃ = 2 кг, m₄ = 0, m₅ = 5 кг. Радиусы : R₅ = 0,2 м , r₅ = 0,1 м , r₄ = 0,1 м ; r₃ = 0,1 м.

Сила F = 2(1+2s) Н ( s – перемещение катка 3 в м). Момент пары сил сопротивления M₄ = 0,6 Нм. Коэффициенты трения: f = 0,2;  = 4мм.

Определить значение скорости V₁ груза 1, в тот момент времени когда перемещение катка достигнет величины  = 2 м .

Решение. Для определения скорости V₁ воспользуемся теоремой об изменении кинетической энергии механической системы (1).

Поскольку в начальный момент времени система находилась в покое, то соответствующая кинетическая энергия T₀ = 0. Кинетическая энергия T системы в конечном состоянии (когда перемещение катка = 2 м) равна сумме кинетических энергий всех тел системы:

(2)

сюда не включены кинетические энергии тел 2 и 4, массы которых равны нулю.

Учитывая, что тело 1 движется поступательно, тело 3 совершает плоскопараллельное движение, а тело 5 - вращается вокруг неподвижной оси, получим :

, , (3)

Все входящие сюда скорости выражаем через искомую V₁ , используя известные из кинематики соотношения:

, , (4)

Входящие в (3) центральные осевые моменты инерции катка 3 (однородного цилиндра) и шкива 5 (масса равномерно распределена по внешнему радиусу R ₅ ) вычисляем по формулам :

, (5)

Подставив выражения (4), (5) для величин _ , V_C3 ,_ , I _C3, I ₅ в (3), получим для кинетической энергии (2) всей системы :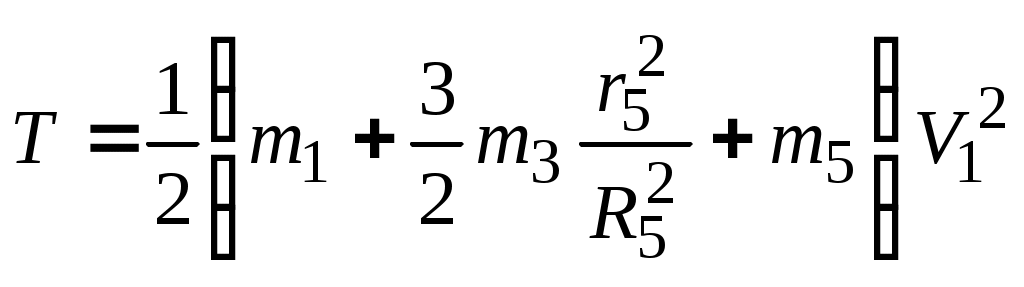

(6)

Теперь найдем сумму работ всех сил, действующих на тела системы, на их перемещениях из начального положения в конечное.

Работа переменной силы F(s) на конечном перемещении  находится в виде интеграла :

(7)

Работы сил тяжести тел системы :

, (8)

где - вертикальное перемещение центра тяжести катка 3;

, (9)

т.к. перемещения центров тяжести тел 1, 5 вдоль вертикали - нулевые.

Работа силы трения груза 1 о плоскость :

, (10)

где - нормальная реакция плоскости, по которой перемещается груз; - перемещение груза 1.

Работа пары сил сопротивления вращению шкива 4 :

, (11)

где - угол поворота шкива 4 .

Пара сил сопротивления качению катка 3 имеет постоянный момент и совершает работу:

, (12)

где N₃=m₃gcos30- нормальная реакция плоскости качения; - угол поворота катка 3.

Работы остальных внешних сил равны нулю:

A(F_сц)=A(N₃)=0, поскольку точка приложения сил F_сц и N₃ является мгновенным центром скоростей катка 3;

A(N₁) = 0, , т.к. сила N₁ перпендикулярна перемещению точки её приложения;

работа реакций осей шкивов (эти силы на рис.3.б не показаны) равна нулю, поскольку точки их приложения не перемещаются.

Все необходимые для вычисления работ линейные и угловые перемещения выражаем через заданное перемещение  центра катка 3, учитывая что зависимости между перемещениями будут подобны зависимостям (4) между соответствующими скоростями :

; ; ; (13)

Находим сумму работ (7) - (12) , учитывая (13) :



(14)

Подставим полученные выражения (6) и (14) в уравнение (1) :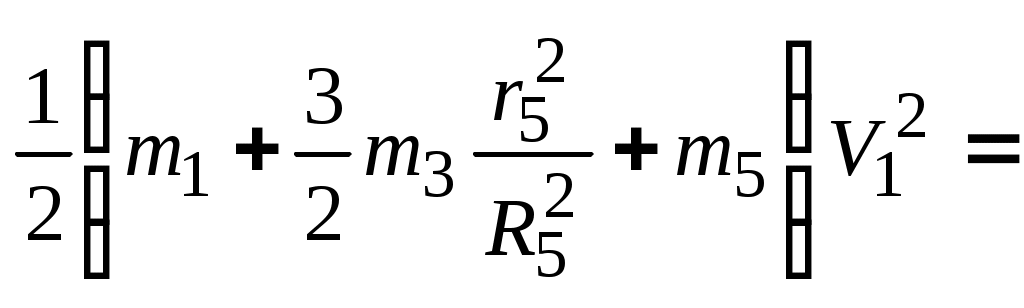





Из последнего равенства выражаем скорость груза 1 :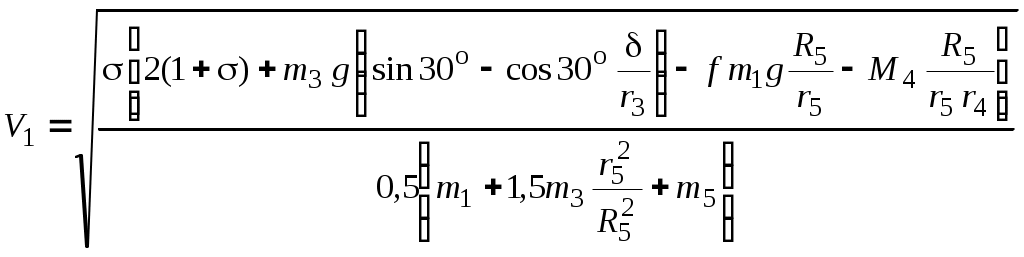



Подставляя числовые значения заданных величин получим V₁ = 0,91м/с.