контра. 1. Выбор задач и варианта Студент должен выбрать для своей контрольной работы задачу С1 и по одной (любой) задаче из разделов Кинематика
 Скачать 1.01 Mb.
|
|
Задача Д3 Вертикальный вал АК (рис.Д3.0-Д3.9), закрепленный подпятником в точке А и цилиндрическим шарниром в точке, указанной во втором столбце табл. 3, вращается равномерно с угловой скоростью = 10 c– 1.  К валу жестко прикреплены: невесомый стержень 1 длиной  с точечной массой m 1 = 6 кг на конце; однородный стержень 2 длиной  массой  . Оба стержня расположены в одной плоскости. Точки крепления стержней к валу а также значения углов , между валом и стержнями даны табл.3. Расстояния АВ = BD = DE = EK = b = 0,4 м .Определить реакции опор вала , и найти динамическую составляющую этих реакций. Таблица 3
Указания. Д3 - задача на применение принципа Даламбера [1], c.344-346. При её решении следует обратить внимание на то, что величина и направление равнодействующей Ф* сил инерции частиц стержня 2 определяется ускорением аС его центра масс, однако линия действия этой равнодействующей через центр масс стержня не проходит. Следует также помнить, что при определении динамических составляющих реакций статические нагрузки (в данной задаче - силы тяжести) не учитываются. Образец выполнения задачи Д3 Условия задачи. Невесомый вертикальный вал АВ, вращается с постоянной угловой скоростью ω = 20 с --1. С валом под углом = 30 0 жестко скреплен однородный стержень DN массой m 1 = 3 кг длиной L = 0,6 м, несущий на конце точечный груз N массой m 2 = 2 кг ( рис.4). Расстояния: DВ = b = 0,4 м , AD = 2b = 0,8 м. Определить реакции подпятника А, подшипника В и найти динамические составляющие этих реакций. Решение. Рассмотрим движение механической системы, состоящей из вала АВ , стержня DN и груза N . Согласно принципу Даламбера все действующие на систему внешние силы вместе с силами инерции образуют уравновешенную систему сил . Изобразим действующие на систему внешние силы: силы тяжести P 1 и P 2 , реакцию подпятника R A и реакцию подшипника R B. Обе реакции считаем расположенными в одной плоскости с валом АВ и стержнем DN ; для упрощения вычислений разложим R A на вертикальную и горизонтальную составляющие X A, Y A (рис.4). О 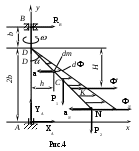 пределим силы инерции частиц стержня DNи груза N .При равномерном вращении вала (ω = const ) элемент стержня DN c массой dm имеет ускорение а, направленное к оси вращения (рис.4) и численно равное a= 2 h(  расстояние от элемента до оси вращения). Сила инерции этого элемента dФ = − (dm)a направлена противоположно его ускорению a (рис.4) и имеет величину  ,пропорциональную расстоянию  от элемента до оси. Следовательно, эпюра сил инерции частиц стержня – треугольник , а их равнодействующая Ф* проходит через центр тяжести К этого треугольника на расстоянии  от точки D (рис.4) .Равнодействующая сил инерции Ф* равна их главному вектору R, который определяется по формуле:  , (С – центр масс стержня) (1) поэтому равнодействующая сил инерции стержня имеет величину Ф*  Н.Сила инерции точечного груза N определяется по формуле ФN= − maNи, следовательно, направлена от оси вращения (рис.4). Ее величина  Выберем вращающиеся вместе с валом АВ координатные оси Ax, Аy так, чтобы стержень DN постоянно лежал в плоскости Axy . Все активные силы (силы тяжести) и силы инерции лежат в плоскости Axy, поэтому уравновешивающие их реакции R A , R B также должны располагаться в плоскости Axy, что и было учтено при изображении реакций (рис.4). Составляем для полученной плоской системы сил уравнения кинетостатики, выражающие условия ее уравновешенности :  ,  ;  ,  ; (2) ,   Подставляя в (2) значения всех заданных и вычисленных величин и решая эту систему уравнений, найдем реакции опор А и В вала:  Н ;  Н ;  Н .Знаки "-" здесь означают, что векторы  и  имеют направления, противоположные указанным на рис.4.Чтобы определить динамические составляющие реакций, полагаем в (2) статические нагрузки P 1 , P 2 равными нулю. После этого находим динамические реакции опор:  Н ;  ;  Н | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||