27. Порядковые и количественные натуральные числа. Счет.Натуральные числа – это числа , которые используют при счете.Счетом элементов множества А называют процесс установления взаимно-однозначного соответствия между множеством А и отрезком натурального ряда. Т.е. счет это действие, позволяющее определить количество чего либо. Счет может быть количественным или порядковым. Количественный счет –это определение количества предметов. Количественные натуральные числа можно определить по вопросу «сколько?».Порядковый счет – это определение количества предметов и место каждого предмета относительно других. Порядковые натуральные числа можно определить по вопросу «какой по счету?», или «какой по порядку?».Таким образом счет элементов множества ведут, используя либо порядковые, либо количественные числа, причем при порядковом счете называется каждый элемент множества, а при количественном – группы предметов счета.
28.Сложение и его свойства.Операцию, при помощи которой находят сумму, называют сложением, а числа, которые складываются – слагаемыми.Выделяют два свойства сложения:-Свойство коммутативности сложения (т.е. переместительное свойство) – для любых целых неотрицательных чисел a и b выполняется равенство a+b=b+a. (От перестановки слагаемых сумма не меняется).-Свойство ассоциативности сложения ( свойство группировки) – для любых целых неотрицательных чисел a,b,cвыполняется равенство (a +b)+c=a+(b+c). ( Чтобы найти сумму трех слагаемых, надо сложить первое слагаемое со вторым и к полученному числу прибавить третье слагаемое или прибавить первое слагаемое к сумме второго и третьего).
29. Смысл отношения равно и меньше над целыми неотрицательными числамиНатуральным числом называется общее свойство класса конечных равномощных множеств.Возьмем множества А и В, пусть a = m(А), b = m(В), где a, bЄN0.Если А
В, то эти множества принадлежат одному классу эквивалентности, поэтому им соответствует одно и то же натуральное число,т.е. a=b.Справедливо и обратное. Если a = b, то эти натуральные числа определяют один и тот же класс конечных равномощных множеств, значит, множества А и В равномощны. Из сказанного можно полу- чить определение равных натуральных чисел.Два целых неотрицательных числа a и b равны тогда и только тогда, когда равномощны множества, число эле- ментов которых числа a и b .Если множества А и В не равномощные, тогда одно из множеств будет равномощно подмножеству другого множества, т.е. или АВ1 ⊂ В, илиВА1 ⊂А.Пусть А
В1 ⊂ В. Видим, что в множе- стве В элементов столько, сколько в множестве А, да еще несколько, так как a = m(А), b = m(В), то говорят, что a < b . Справедливо и обратное. Если a < b, то А
В1 ⊂ В, где a = m(А), b = m(В).Натуральное число a меньше натурального числа b тогда и только тогда, когда множество, число элементов которого равно a, равномощно собственному подмножеству другого множества, число элементов которого равно b.
Вопрос30: Отношения "больше на" и "меньше на" При решении задач в практической деятельности часто требуется не только установить, что число а меньше или больше числа b, но и узнать насколько а меньше или больше b.чтобы узнать, на сколько одно число меньше или больше другого, надо из большего числа вычесть меньшее.Рассмотрим, например, задачу: Во дворе гуляли 6 мальчиков, а девочек на 2 меньше. Сколько было девочек? Чтобы узнать ответ, из большего вычитаем меньшее. 6-2=4. Естественно, что при решении таких задач в начальной школе объяснение будет выглядеть иначе, но суть его от этого не изменится.
31.Умножение и его свойства.Действия с помощью которого находят произведение чисел: а*b, называется умножением, а числа, которые умножают называют множители.-Произведение целых натуральных неотрицательных чисел: а*в называется такое целое неотрицательное число а*b, которое удовлетворяет следующим условиям:а*b, когда b множитель а содержание.Несколько элементов мн. А:а*b=а, если в=1а*b=0, если в=0-произведение целых неотрицательных чисел а иb можно рассматривать, как число элементов декартово произведения множеств а иb.Свойства умножения:-Коммуникативности: для любых целых неотрицательных чисел а и в свойственно или справедливо равенство: а*b=b*а;-Ассоциативности: для любых целых неотрицательных чисел а и b свойственно равенство: (а*b)*с=а*(b*с);-Дистрибутивности относительно сложения: для любых целых неотрицательных чисел а, b, с, справедливо или свойственно равенство: (а+b)*с=ас*bс; Дистрибутивности по отношению к вычитанию: для любых целых натуральных чисел а, b, с, справедливо равенство: (а-b)*с=(а*с)*(b*с).
32.Деление и его свойства.Действия с помощью которых находят частное чисел а:bназывается делением, где число а – делимое, b – делитель. -Ни одно число нельзя делить на ноль-При делении нуля на число получается ноль-при делении любого числа на 1 получается это же число -если делимое или делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится. Частным целого неотрицательного числа а и натурального числа bназывают такое целое неотрицательное число с=а:b произведение каждого и числа b=а. Поэтому говорят, что деление есть действие, обратное умножению.
Свойства деления:1.А:b, если а≥ b. 2.А=0, b € N, 0:b=0.3.A € N, b=0 a:0≠0.4.A € N, b=1, a:1=a. 5.(a:b):c=a:(b:c).6.(a+b):c=a:c+b:c(48+36):2=24+18=42.7.(a-b):c=a:c-b:c.
33)Отношения "больше в" и меньше в".Первое знакомство с отношениями больше в и меньше в происходит в начальной школе.Чтобы узнать во сколько раз одно число больше или меньше другого, необходимо большее число разделить на меньшее.Пусть дано множество А, в котором 6 элементов, и множество В с двумя элементами. выделим в множестве А подмножества равномощные множеству В. Их 3. В этом случае доказывают что число 6 больше числа 2 в 3 раза, а число 2 меньше числа 3 в 3 раза.Например: Посадили 3 дуба и 12 берез. Во сколько раз меньше посадили дубов, чем берез? 12:3=4. В 4 раза меньше
34)Традиционная и альтернативная системы обучения математике младших школьников. В методических публикациях последнего двадцатилетия часто встречаются слова «традиционная система», «альтернативная система» обучения. Поясним происхождение и смысл этих названий.В Советском Союзе учителям разрешалось работать только по тем учебникам, которые были утверждены и рекомендованы Министерством образования. В 1968 г. был объявлен конкурс на написание учебника по математике для начальной школы. Из всех предложенных был выбран и утвержден учебник, написанный авторским коллективом под руководством М.А. Бантовой и М.И. Моро. Этот учебник стали называть "традиционным". Долгие годы он был единственным для обучения математике в начальной школе. На всей территории бывшего Советского Союза, учились по одному и тому же учебнику и по единому учебному плану. После развала Советского Союза стали публиковаться учебники других авторов, эти учебники стали называть «альтернативными». Некоторые из них были написаны еще в 70-е годы XX в. Сегодня альтернативным называют любой новый учебник по отношению к традиционному. Иногда в литературе можно встретить утверждение, что традиционным учебник Бантовой и Моро назван потому, что он не имеет развивающей направленности. Однако с методических позиций очевидно, что развивающая направленность урока более зависит от методики работы учителя.Многолетний опыт апробации различных альтернативных учебников показал, что для получения развивающего эффекта недостаточно просто использовать в работе учителя новый учебник. Необходимо владеть методикой математического развития ребенка, чтобы реализовать развивающую функцию математического содержания учебника.Для учителя важно научиться анализировать появляющиеся варианты учебников, понимать их содержательные и методические отличия, их соответствие обязательному минимуму образования. Проведение такого предварительного анализа необходимо для прогнозирования результатов обучения и хода обучающего процесса.
35. Особенности обучения математике по системе Д.Б. ЭЛЬКОНИНА- В.В. ДАВЫДОВА.Система развивающего обучения Д.Б.Эльконина-В.В.Давыдова существует более 40 лет, проверена временем, завоевала всеобщее признание.Фундамент системы составляет концепция развивающего обучения, в которой ребенок рассматривается не как обучаемый индивид, не как объект обучающих воздействий, а как самоизменяющийся субъект учения, как учащийся. В основу этой системы развивающего обучения легли результаты исследований психологических особенностей детей младшего школьного и подросткового возраста, проведенных выдающимся российским ученым Л.С. Выготским и его последователями.В программах для начальных классов комплекта Д.Б.Эльконина – В.В.Давыдова представлена система лингвистических и математических понятий, усвоение которых позволяет ученикам самостоятельно и осознанно находить способы решения широкого круга практических и познавательных задач.Содержание учебных предметов, прежде всего, должно способствовать формированию у младших школьников основ теоретического мышления. Последнее складывается в процессе выполнения учащимися учебной деятельности. Поэтому содержание учебных предметов в системе Д.Б. Эльконина – В.В. Давыдова разработано в соответствии с особенностями и структурой учебной деятельности школьников.В результате обучения по системе Эльконина – Давыдова дети в состоянии аргументировано отстаивать свою точку зрения, учитывать позицию другого, не принимают информацию на веру, а требуют доказательств и объяснений.Обучение в школе по системе развивающего обучения Эльконина – Давыдова доступно каждому ребенку. Оно развивает всех детей с различными исходными условиями их интеллекта и личности.
36. Площадь геометрической фигуры.Площадь – это численная характеристика геометрической фигуры, показывающая размер данной фигуры. 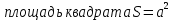 .площадь прямоугольникаS= ab.площадь треугольника .площадь прямоугольникаS= ab.площадь треугольника 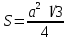 площадь параллелограмма S= ahплощадь ранобед.треугS площадь параллелограмма S= ahплощадь ранобед.треугS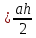 .площадь трапеции .площадь трапеции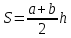 .площадь прямоуг.треуг .площадь прямоуг.треуг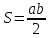 .площадь ромба .площадь ромба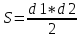 .площадь круга .площадь круга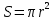
37. Объем геометрического тела.Геометри́ческое те́ло — связная часть пространства, ограниченная замкнутой поверхностью своей наружной границы. Геометрическое тело можно определить замкнутой поверхностью, которая будет являться его границей.Фигура, все точки которой не находятся на одной плоскости, называется объёмной фигурой. Ограниченная часть пространства называется геометрическим телом, а множество точек, ограничивающих его от окружающего пространства, называется поверхностью этого тела.Главная величина геометрических тел — это их объём.Объём геометрического тела — это величина, которая описывает занимающую этим телом часть пространства.Свойства объемов:-За единицу измерения объемов принимают объем куба с ребром, равным единице;-Равные тела имеют равные объемы;-Если тело можно разбить на несколько простых тел, то его объем равен сумме объемов составляющих тел. V - объем, S - площадь поверхности, R - радиус основания, L - образующая, h - высота, P - периметр. Цилиндр - это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.V=П(число пи) R^2h S=2Sосн + Sбок=2ПR^2+ПRh Конус - это геометрическое тело, образуемое вращением прямоугольного треугольника вокруг катета.V=⅓(дробь) Sосн h
S=Sосн+Sбок=ПR^2+ПRL..L=(знак корня) корень из R^2+h^2Шар - это тело, состоящее из всех точек пространства, которые находятся на расстоянии, не большем данного от данной точки. Проходящий через центр шара отрезок, который соединяет две точки шаровой поверхности, называется диаметром.V=4/3 ПR S=4 ПR^2
Прямоугольный параллелепипед - это многогранник с шестью гранями, каждая из которых является в общем случае прямоугольником. Противолежащие грани параллелепипеда равны. Рёбра параллелепипеда, сходящиеся в одной вершине взаимно перпендикулярны.V=abc. S=2(ab+bc+ac).Прямая призма - это призма, у которой боковые ребра перпендикулярны плоскости основания, откуда следует, что все боковые грани являются прямоугольниками. Другие призмы называются наклонными. ... Правильная призма — это прямая призма, основанием которой является правильный многоугольник.V=Sосн h.S=Sбок+2Sосн…Правильная пирамида - многогранник, у которого одна грань, называемая основанием, – многоугольник, а другие грани – треугольники с общей вершиной, называется пирамидой.Свойства правильных пирамид:-Боковые ребра правильной пирамиды - равны;-Боковые грани правильной пирамиды - равные друг другу равнобедренные треугольники.V=⅓ h a^2.Произвольная пирамида V=⅓ Sосн h..S=½ P L…S=Sбок+Sосн
38.Формирование умественных дейсвтий при изучении гео-го материала в 1 кл. Многочисленные наблюдения педагогов показали, что ребенок, не научившийся учиться, не овладевает примерами мыслительной деятельности в начальных классах школы, а в средних обычно переходит в разряд неуспевающих. Математика способствует развитию у ребёнка мышления, творческого воображения памяти, внимания, строгой последовательности, наблюдательности, рассуждения и его доказательности; дает реальные предпосылки для дальнейшего развития наглядно-действенного и наглядно-образного мышления учащихся. Такому развитию способствует изучение геометрического материала, связанного с алгебраическим и арифметическим материалом. Изучение геометрического материала обеспечивает числовую грамотность учащихся, дает им начальные геометрические представления, развивает наглядно-действенное и наглядно-образное мышление и пространственное воображение детей, формирует у них элементы конструкторского мышления и конструктивных умений.Данное умение является необходимым условием социального бытия человека, формой отражения окружающего мира, условием успешного познания и активного преобразования действительности. Свободное оперирование пространственными образами является тем фундаментальным умением, которое объединяет разные виды учебной и трудовой деятельности. Оно рассматривается как одно из профессиональных важных качеств.
41. Деление с остатком.Разделить с остатком целое неотрицательное числоа на натуральное число b– это значит найти такие целые неотрицательные числаg и r, что а =bg + r и 0 ≤ r
42.Длина отрезка и велечина угла.Длиной отрезка называют положительную величину, определенную для каждого отрезка и обладающую следующими свойствами:-Равные отрезки имеют равные длины;-Если отрезок состоит из конечного числа отрезков, то его длина равна сумме длин этих отрезков;-Существует отрезок длина которого равна 1.Величиной угла называют положительную величину, определенную для каждого угла и обладающую свойствами:-Равные углы имеют равные величины;-Если угол состоит из конечного числа углов, то его величина равна сумме величин этих углов;-Существует угол, величина которого равна 1.
43.Из истории возникновения геометрии.Геометрия зародилась в Древнем Египте как набор правил решения практических задач, возникавших в строительстве, при распределении земельных участков, измерении площадей, объемов и т.д. Особенно важной была задача распределения земельных наделов. Этим занимались специальные люди — землемеры, которых греки называли гарпедонаптами, т. е. натягивателями веревок, так как при распределении земли использовались веревки. Но чтобы знать, где и как их натягивать, надо было иметь план полей. Так практическая задача распределения земельных участков привела к возникновению науки геометрии. Обширные сведения о свойствах фигур, накопленные египтянами, были заимствованы греками. Произошло это в VII—V ав, До н. э. А так как особенно важной задачей было землемерие, то греки назвали науку о фигурах геометрией (от греч. геос — земля и метрио — измеряю). Многие геометрические понятия возникли в результате многократных наблюдений реальных предметов той или иной формы, т.е. в процессе познания окружающего мира люди знакомились и с простейшими геометрическими формами. Развитие землемерия, обобщение накопленного опыта наблюдений привело к созданию практических правил измерения земельных участков, нахождения площадей и объемов простейших фигур, строительных норм и др. Так, формулы для вычисления площадей земельных участков, имеющих форму треугольника, трапеции, встречаются у древних египтян, вавилонян. К ХVII—XVI вв. до н. э. были установлены такие факты, как теорема Пифагора, выражение для подсчета объема шара и многие другие. Но выступали они не как логически доказанные утверждения, а как выводы из опыта. Таким образом, геометрия возникла как прикладная наука, как собрание правил, необходимых для решения практических задач, таких как сравнение фигур, нахождение геометрических величин, а также для простейших геометрических построений. Возникло доказательство, правила стали превращаться в теоремы, которые доказывались без прямых ссылок на опыт. Вообще, совершенствование геометрических знаний шло по пути их отделения от опыта — в результате предметом геометрии стали не реальные, а идеальные фигуры, т.е. фигуры, являющиеся образами предметов, в которых абстрагируются от всего, кроме формы. Более того, эти фигуры стали дополняться свойствами, которыми реальные предметы не обладают.
Первым, кто построил новую геометрию, был Н. И. Лобачевский, профессор Казанского университета. В конце XIХ в. немецкий математик Д. Гильберт подвел итог исследованиям в области логически строгого построения евклидовой геометрии. В евклидовой геометрии изучают свойства фигур, связанные с понятиями длины, величины угла, площади и объема. Такие свойства фигур называются метрическими.
|
 Скачать 72.82 Kb.
Скачать 72.82 Kb.
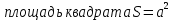 .площадь прямоугольникаS= ab.площадь треугольника
.площадь прямоугольникаS= ab.площадь треугольника 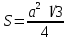 площадь параллелограмма S= ahплощадь ранобед.треугS
площадь параллелограмма S= ahплощадь ранобед.треугS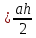 .площадь трапеции
.площадь трапеции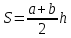 .площадь прямоуг.треуг
.площадь прямоуг.треуг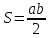 .площадь ромба
.площадь ромба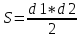 .площадь круга
.площадь круга