10 ТЕМА. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. 10. обыкновенные дифференциальные уравнения содержание 1
 Скачать 1.72 Mb.
|
|
Решение линейного дифференциального уравнения первого порядка Общее решение ищется в виде  где  некоторые функции.Покажем на примере, что любую функцию  можно представить в виде произведения двух функций, одна из которых выбирается произвольно, а вторая зависит от этого выбора.Пусть  . Можно  представить в виде различных пар множителей:   где первый множитель выбирается произвольно. Указанная подстановка  приводит линейное д.у.1 к решению двух д.у. с разделяющимися переменными. Покажем это в общем виде. В линейное уравнение  подставим  Получим или  . (4)Выберем функцию u такой, чтобы  (5)Уравнение (5) – дифференциальное уравнение с разделяющимися переменными:  Интегрируя, найдем функцию  без учета произвольной постоянной. Подставим найденную функцию  в уравнение (4) и получим  дифференциальное уравнение с разделяющимися переменными (3). Его общее решение позволит получить второй множитель  Тогда  общее решение линейного д. у. 1.Пример 1. Найти общее решение уравнения  Решаем подстановкой  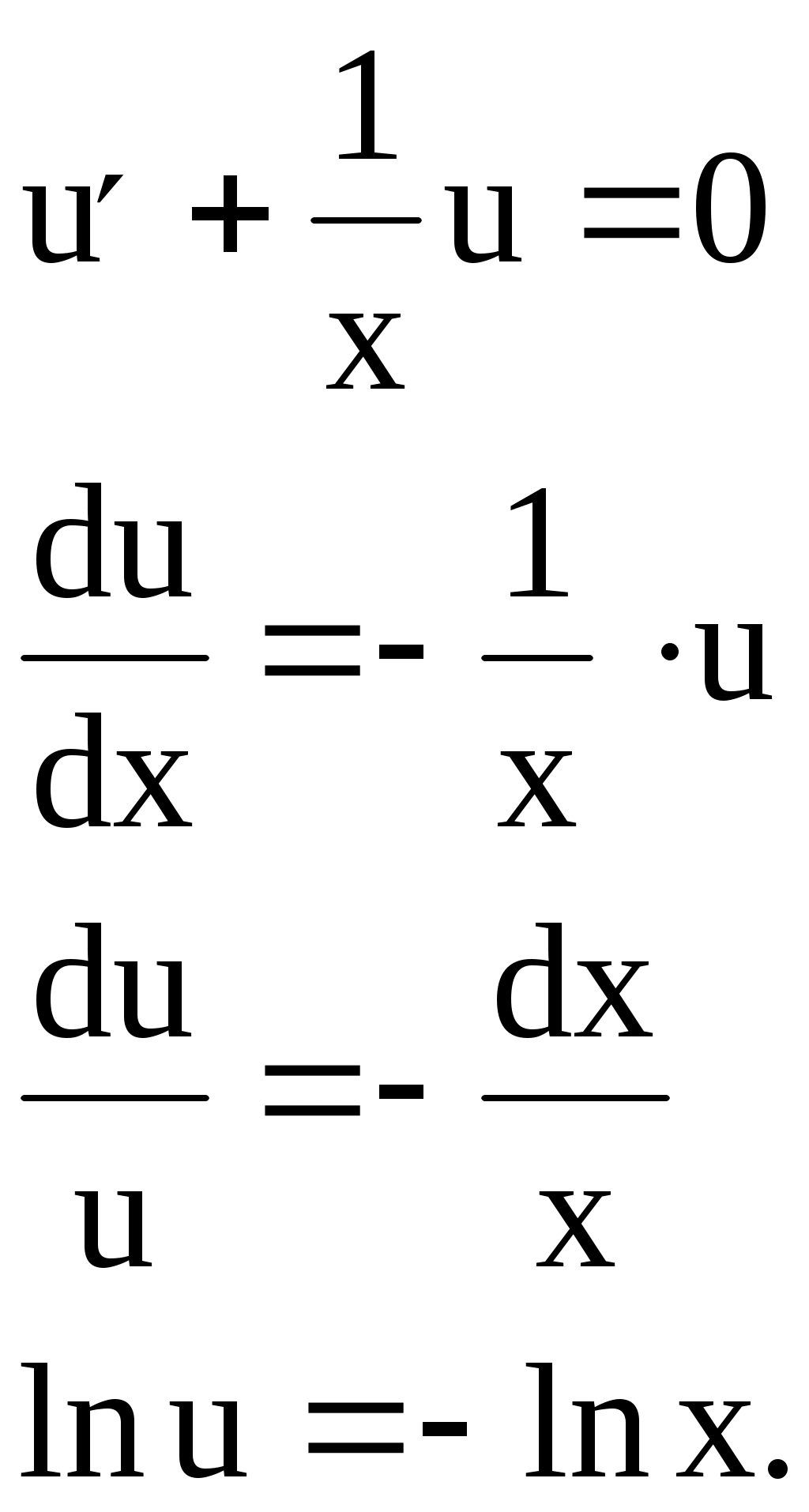 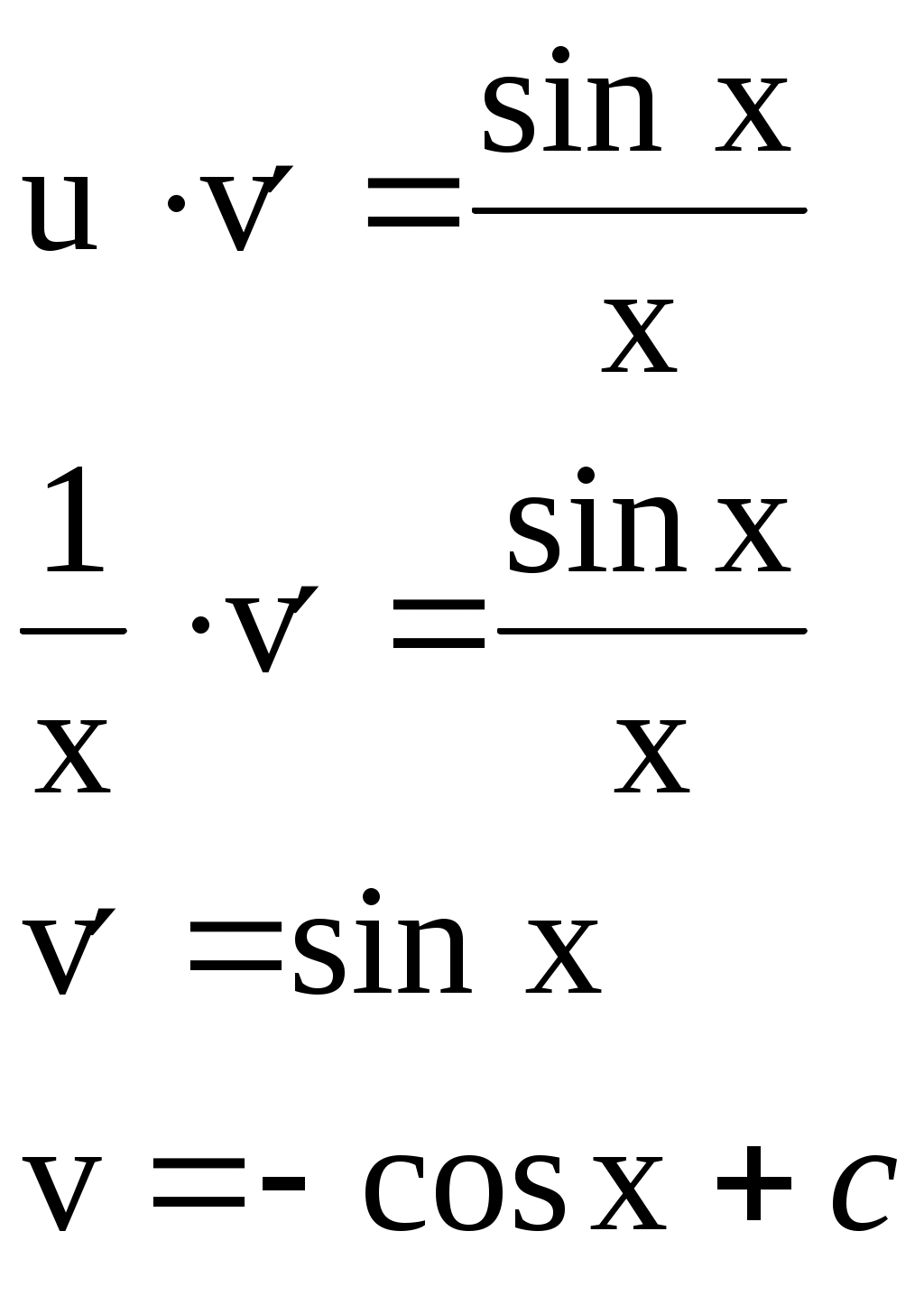 (6)    подставим в (6).Общее решение:  Пример 2. Найти частное решение дифференциального уравнения  Подстановка: .    (7)   Подставим найденную функцию u в уравнение (7):       Таким образом, общее решение данного уравнения будет иметь вид  или  Найдем частное решение дифференциального решения, удовлетворяющее начальному условию   Следовательно, искомое частное решение такое:  Уравнения, приводящиеся к линейным (уравнения Бернулли) Уравнение вида  называется уравнением Бернулли. Здесь n – действительное число, причем при n = 0 получим линейное уравнение; при  получим уравнение с разделяющимися переменными. При  уравнение Бернулли приводится к линейному, поэтому решается подстановкой  Пример. Найти общее решение уравнения  Разделив левую и правую части уравнения на х, представим его в виде  . Можно утверждать, что это уравнение имеет общий вид т. е. является уравнением Бернулли. Решаем его подстановкой   где  – вспомогательные функции.Подставим  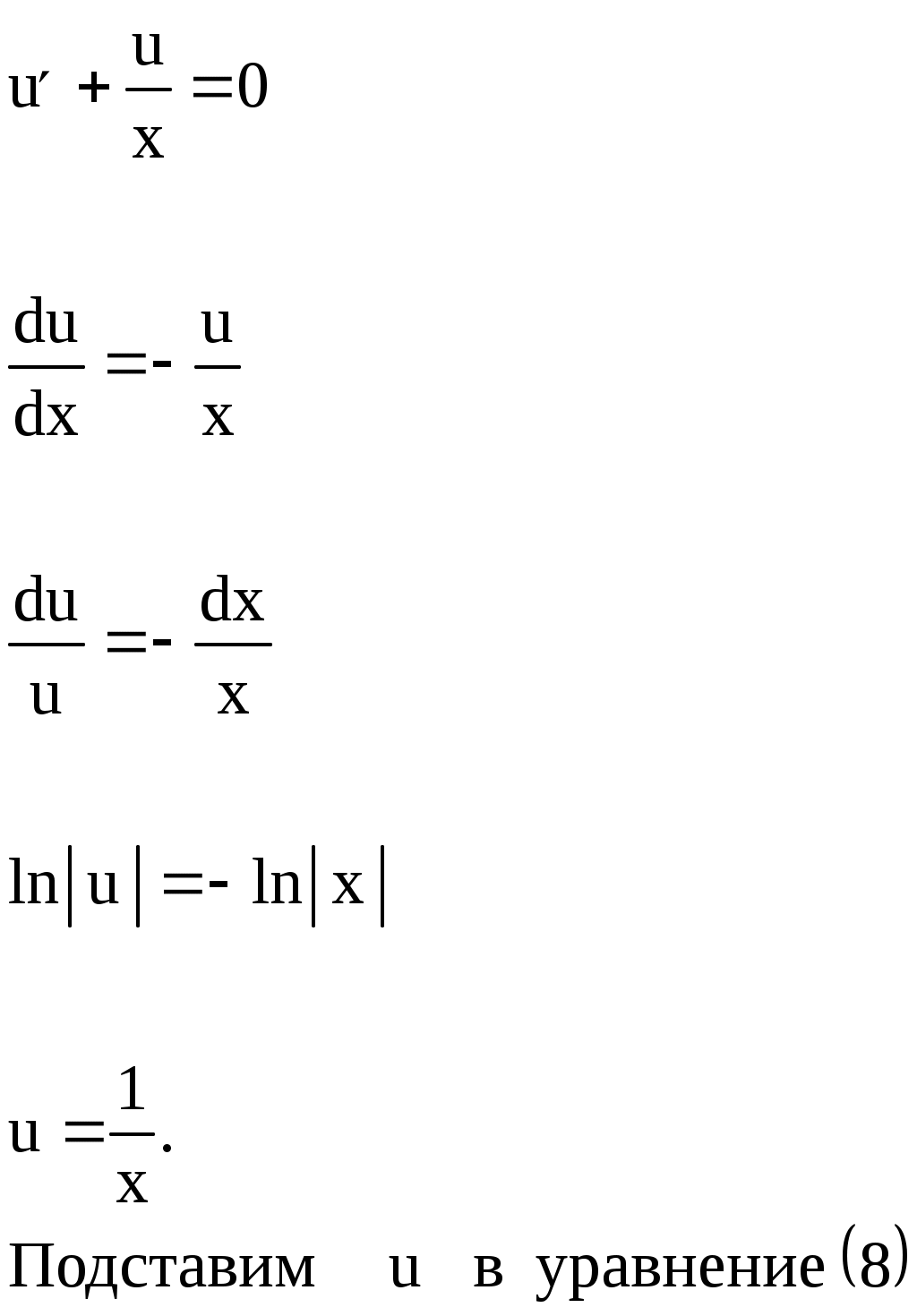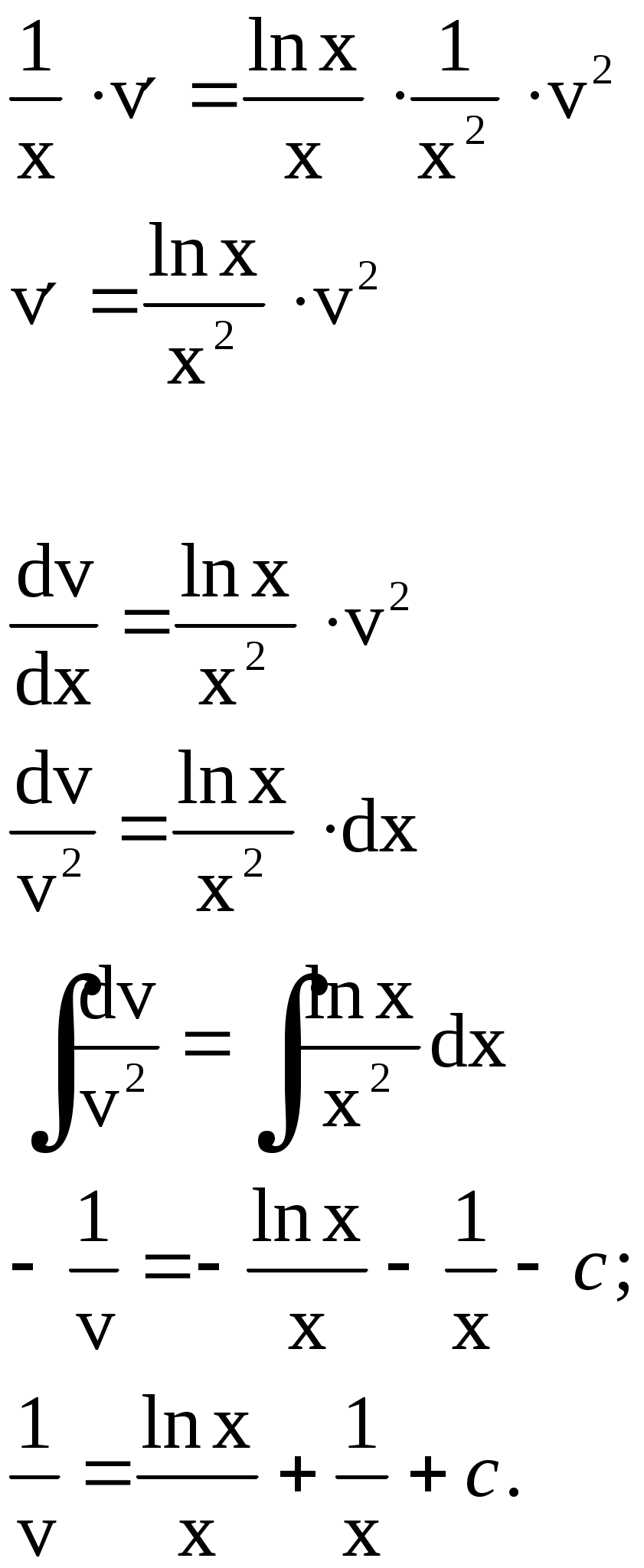в исходное уравнение:  (8)    Для получения общего интеграла найдем   или  .Замечание. Неопределенный интеграл  найден с применениемформулы интегрирования по частям:  Производим подстановку   ;   .Тогда   4. Дифференциальные уравнения второго порядка Дифференциальное уравнение второго порядка (д.у. II) содержит вторую производную некоторой функции, саму эту функцию, независимую переменную и первую производную. Д.у. II может быть записано в виде  или  Определение. Общим решением д.у.II называется функция  зависящая от двух произвольных постоянных  , такая, чтоона удовлетворяет уравнению при любых значениях постоянных  каковы бы ни были начальные условия  , можно найти такие значения  при которых функция  удовлетворяет этим условиям.Определение. Всякая функция, полученная из общего решения при конкретных значениях постоянных  , называется частным решением д.у.II.Заметим, что начальные условия для д.у. II представляют собой заданные значения функции и ее производной  при одном и том же данном значении независимой переменной  Их обычно записывют   или  т. е. задать начальные условия для нахождения частного решения д.у. II – значит задать три числа:  Пример. Дано д.у.II  . Проверим, что его общим решением является функция Найдем первую и вторую производные этой функции  Подставив  в данное уравнение, получим или  –верное равенство. Найдем частное решение этого уравнения при заданных начальных условиях 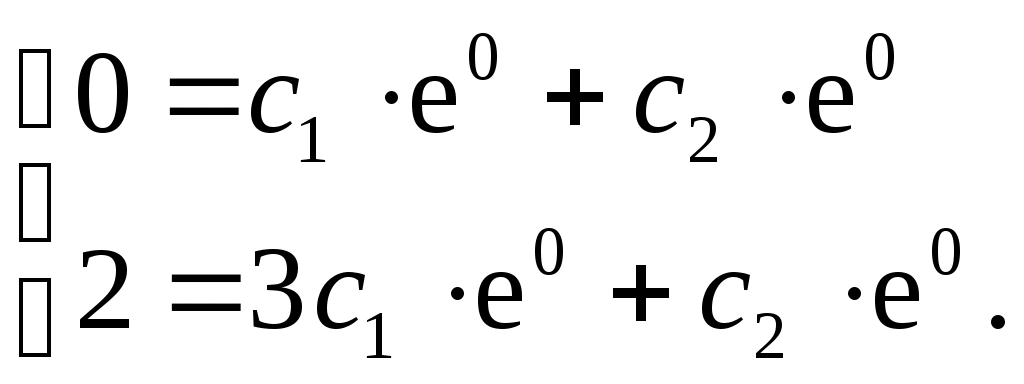 Подставим эти условия в выражения yи    или 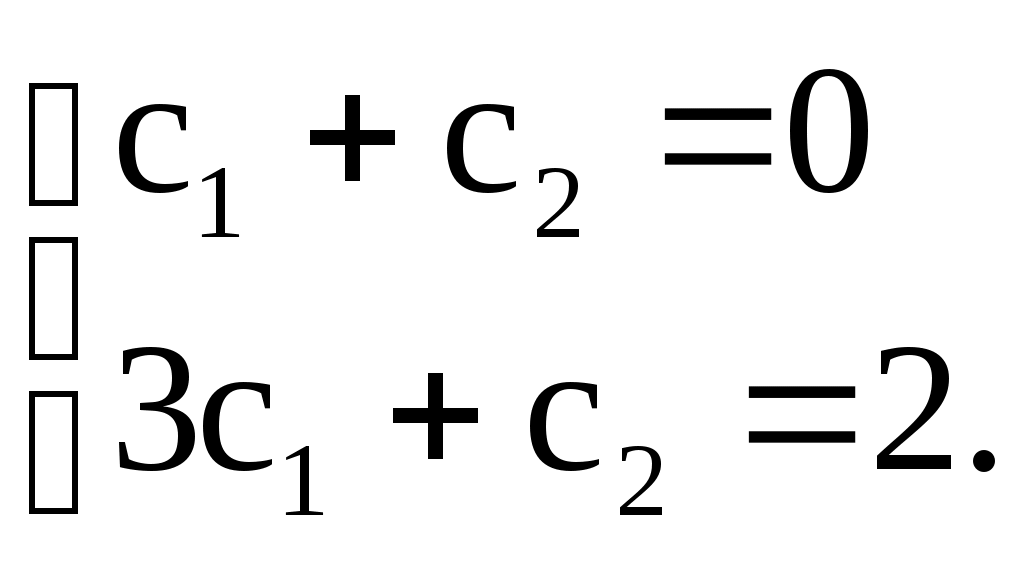 Решив эту систему, получим значения постоянных   при которых из общего решения  выделим искомое частное решение Рассмотрим некоторые типы дифференциальных уравнений второго порядка и способы их решения. 5. Дифференциальные уравнения второго порядка, допускающие понижение порядка Рассмотрим некоторые типы д.у. II, решение которых сводится к решению дифференциальных уравнений первого порядка. 1-й тип. Простейший тип таких уравнений – это  Дифференциальное уравнение содержит только вторую производную и некоторую функцию от х (ни сама функция y, ни ее первая производная  в уравнение не входят). Уравнение вида  решается последовательным интегрированием два раза.Пример 1.   Получили уравнение первого порядка  отсюда  –общее решение исходного уравнения (содержит две произвольные постоянные  и  ).Аналогично решаются и дифференциальные уравнения порядков выше второго, если они имеют такой же вид, например:  Пример 2.     –общее решение данного уравнения. Пример 3.      –общее решение уравнения. Обратите внимание, общее решение дифференциального уравнения третьего порядка содержит три произвольные постоянные  , а дифференциального уравнения четвертого порядка – уже четыре  Допускают понижение порядка и дифференциальные уравнения вида  |