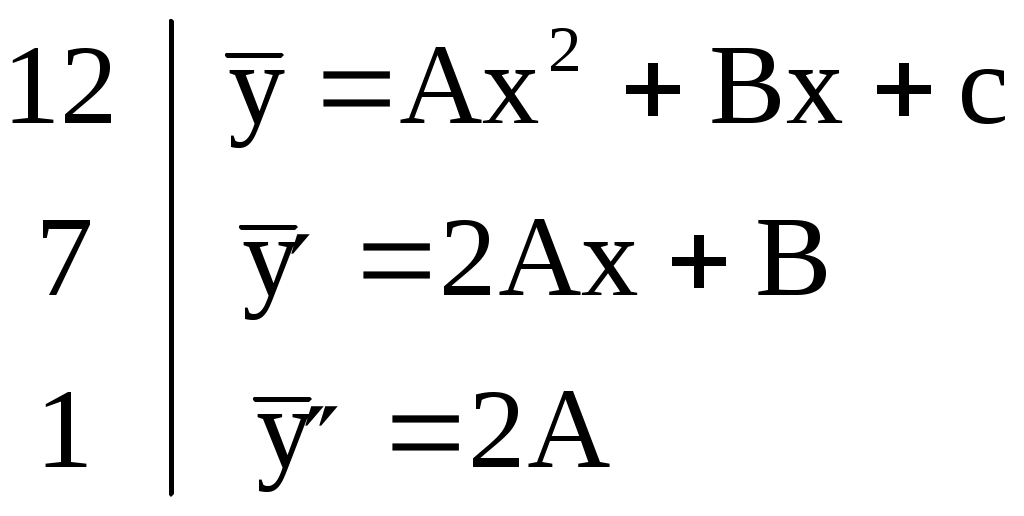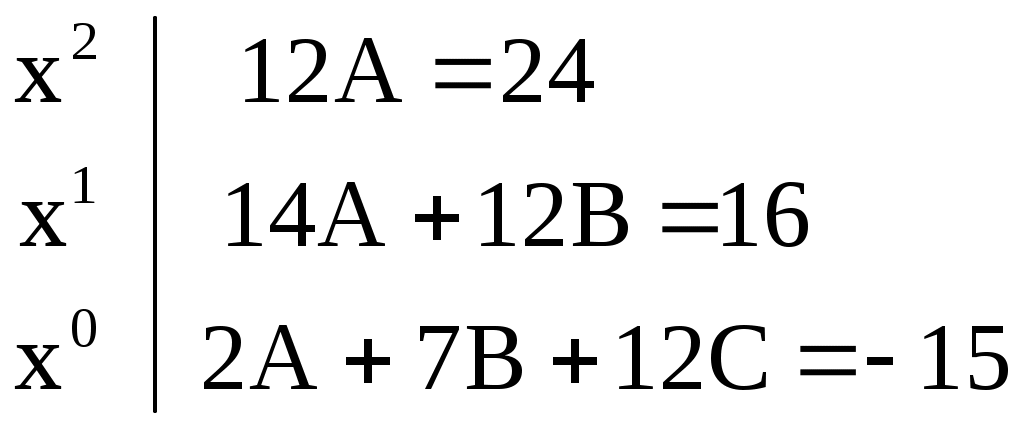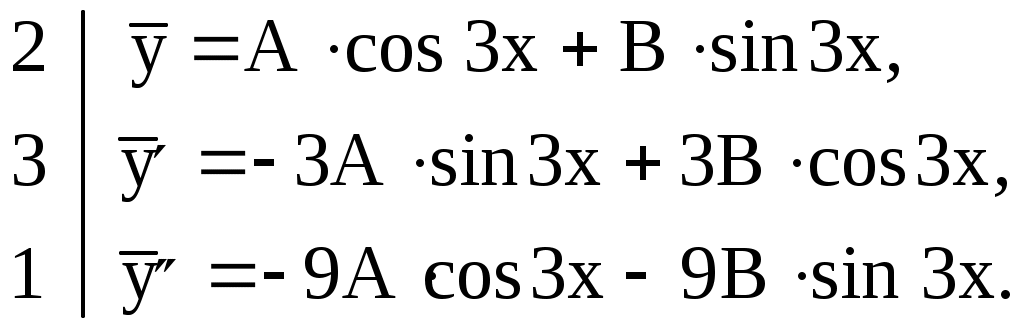|
|
10 ТЕМА. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. 10. обыкновенные дифференциальные уравнения содержание 1
Линейные неоднородные дифференциальные уравнения
второго порядка
Линейное неоднородное уравнение отличается от однородного функцией в правой части. Линейное неоднородное уравнение имеет вид
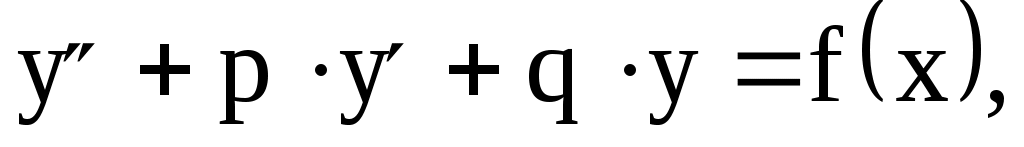
а соответствующее ему линейное однородное уравнение –
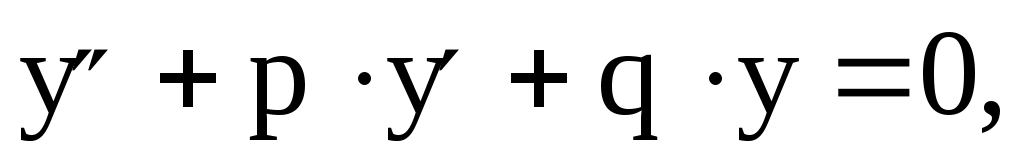
которое, как известно, решается с помощью характеристического уравнения (16)
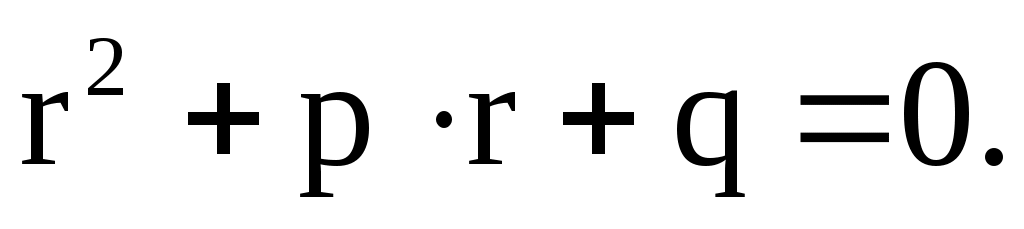
Сформулируем теорему о структуре общего решения неоднородного уравнения (13).
Теорема 2. Общее решение неоднородного линейного дифференциального уравнения равно сумме какого-либо частного решения этого уравнения и общего решения соответствующего однородного уравнения.
Пусть y– общее решение уравнения (13)
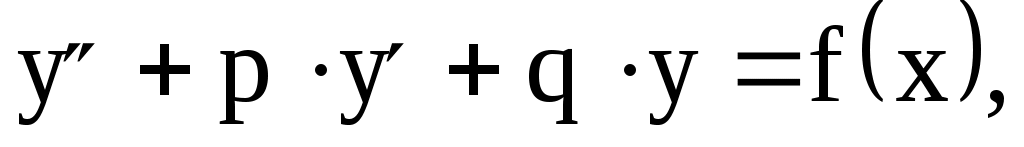
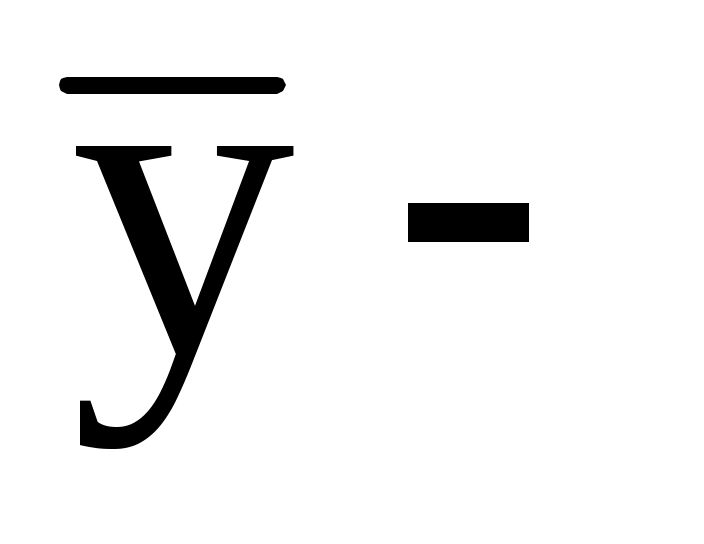 какое-либо частное решение уравнения (13), какое-либо частное решение уравнения (13),
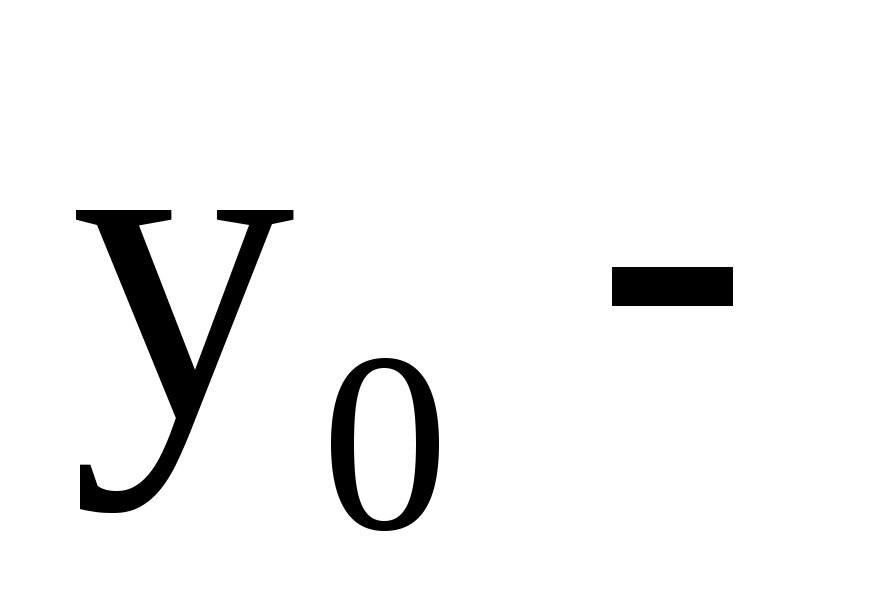 общее решение соответствующего однородного уравнения (14) общее решение соответствующего однородного уравнения (14)
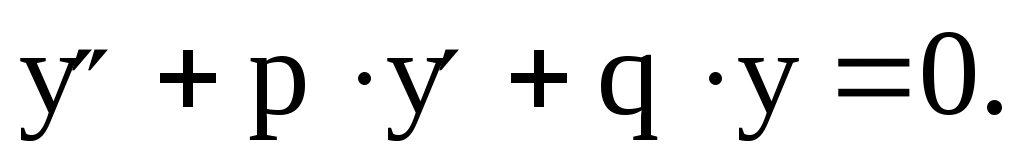
Тогда 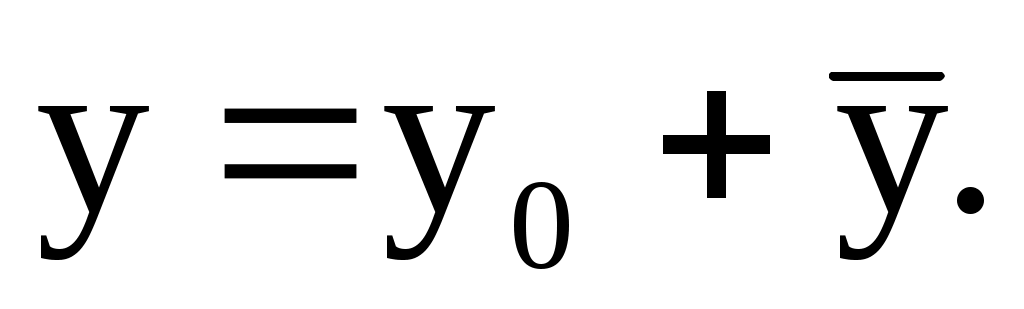
Таким образом, основная задача при решении неоднородного линейного д.у. II состоит в нахождении какого-либо частного решения.
Укажем один из методов нахождения частного решения неоднородного уравнения , когда правая часть уравнения 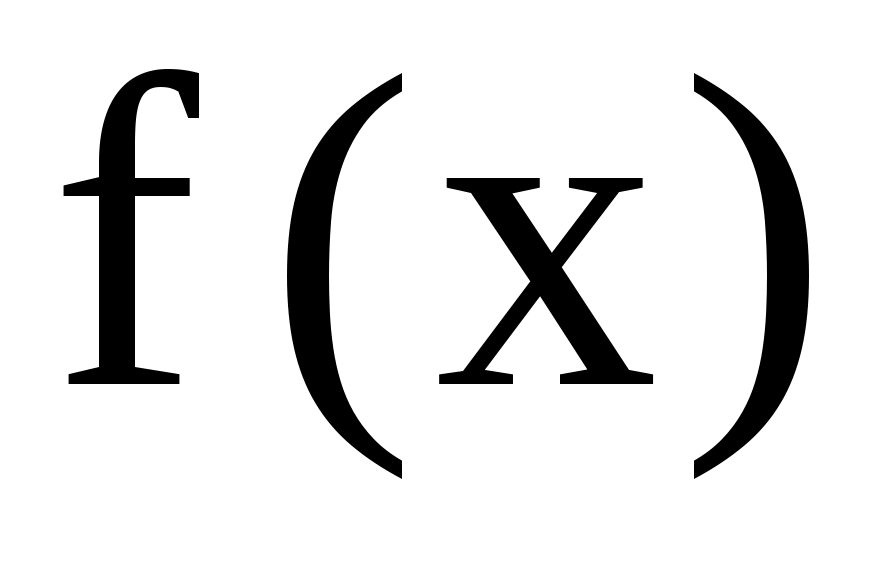 имеет специальный вид. К таким функциям имеет специальный вид. К таким функциям 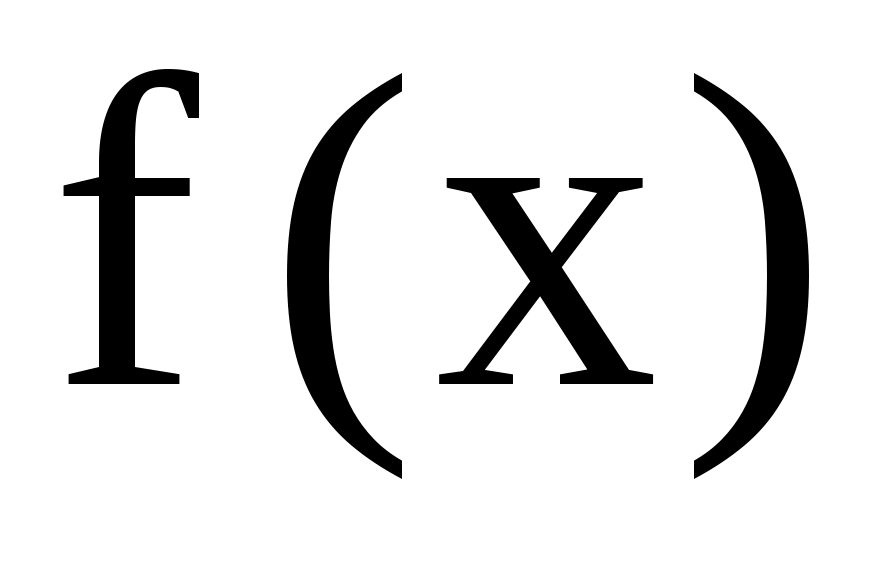 относятся следующие функции: экспонента относятся следующие функции: экспонента 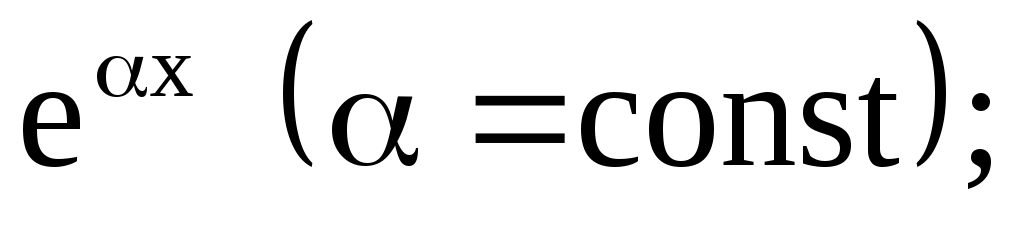 многочлены n-й степени относительно переменной х многочлены n-й степени относительно переменной х 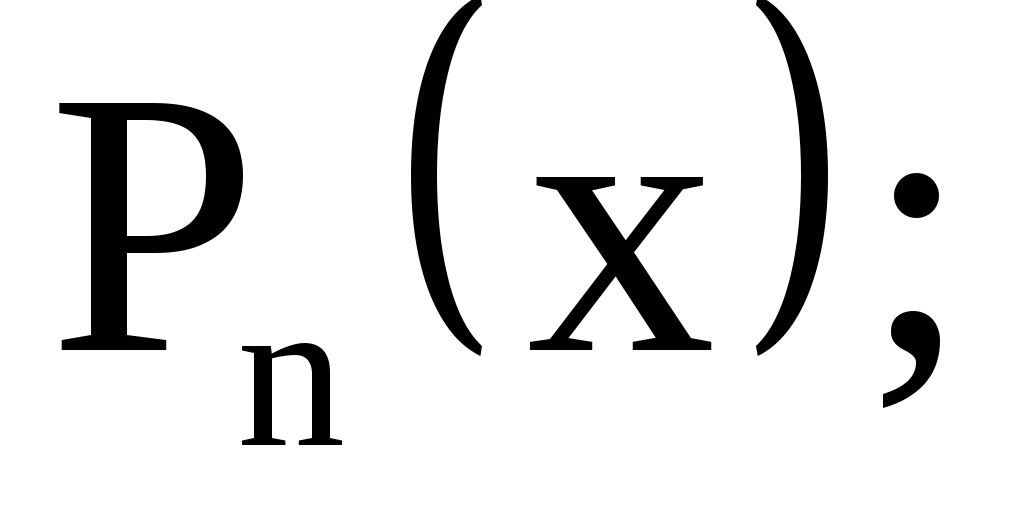 тригонометрические функции тригонометрические функции 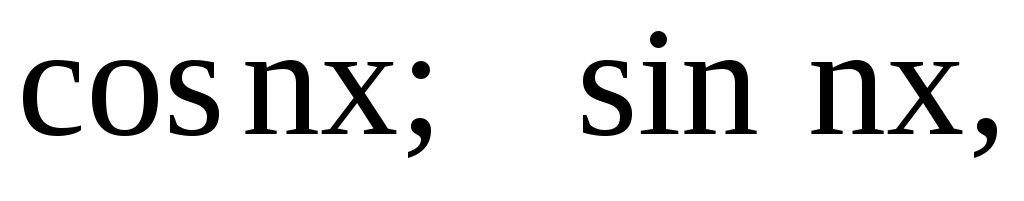 а также их произведения. а также их произведения.
Метод неопределенных коэффициентов
Этот метод иначе называется методом подбора частного решения 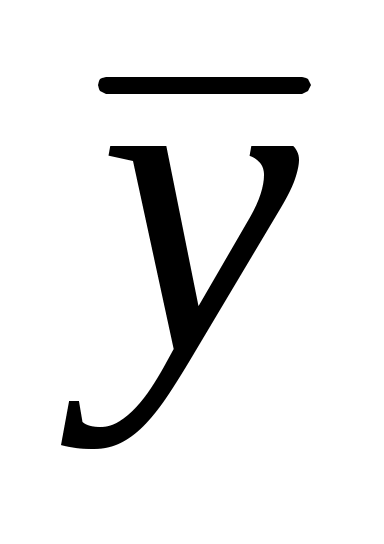 уравне-ния (13) по виду правой части уравне-ния (13) по виду правой части 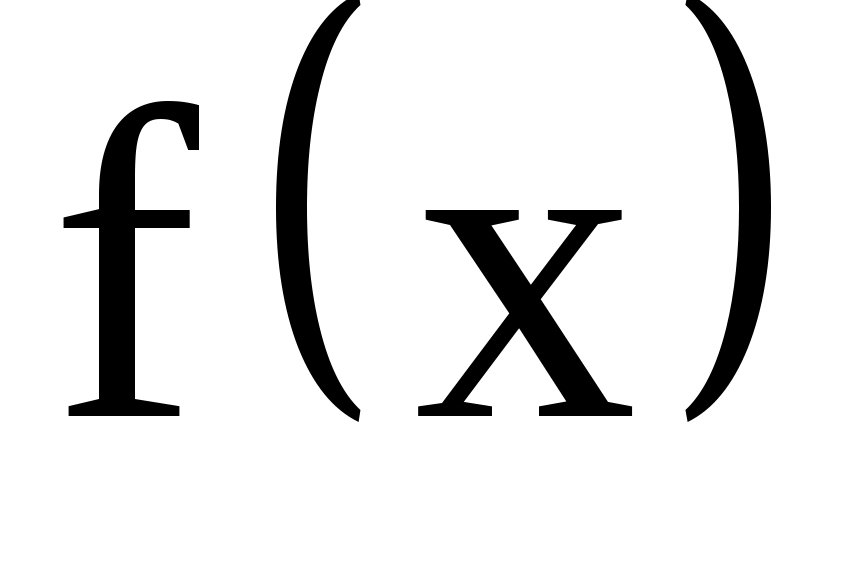 . .
Пусть правая часть 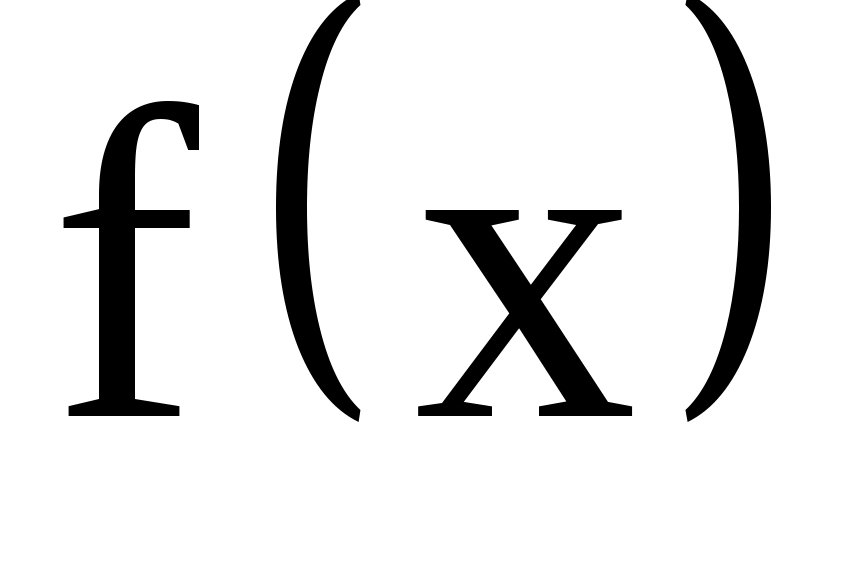 уравнения уравнения
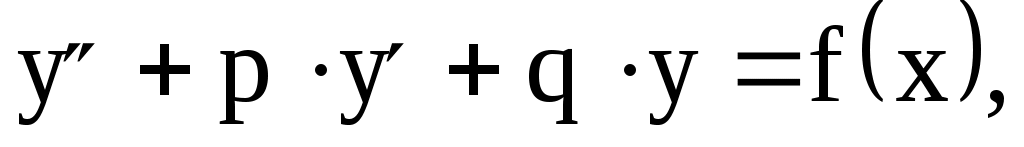
имеет вид 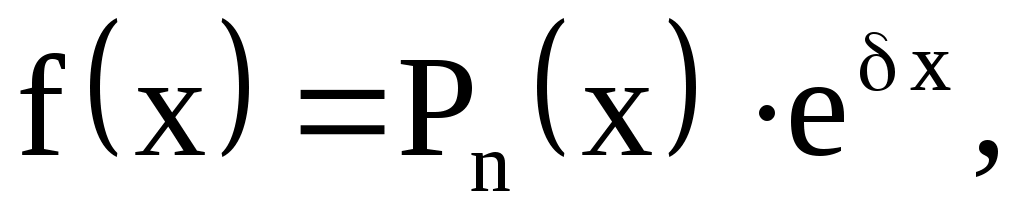 т. е. представляет собой произведение экспоненты на многочлен, где т. е. представляет собой произведение экспоненты на многочлен, где 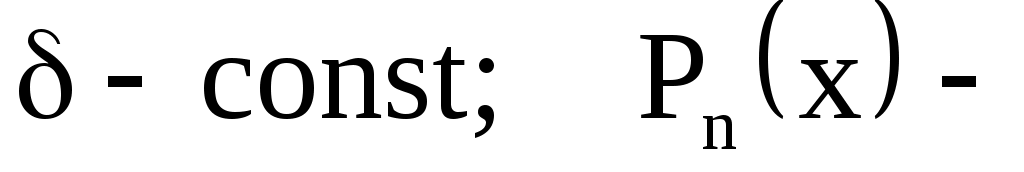 многочлен n-й относительно х. Тогда возможны следующие случаи. многочлен n-й относительно х. Тогда возможны следующие случаи.
Число 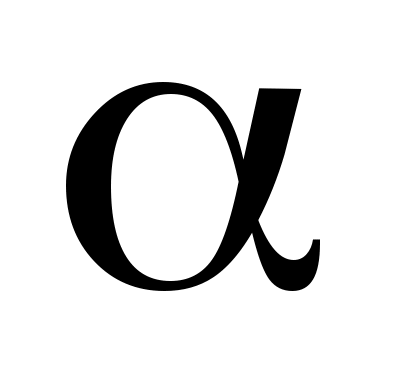 не является корнем характеристического уравнения (16) не является корнем характеристического уравнения (16)
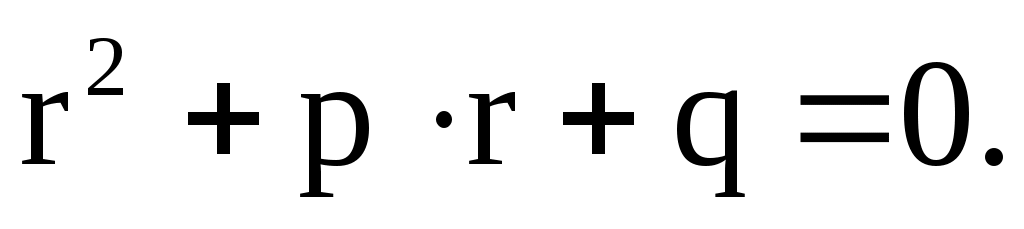
В этом случае частное решение нужно искать в виде 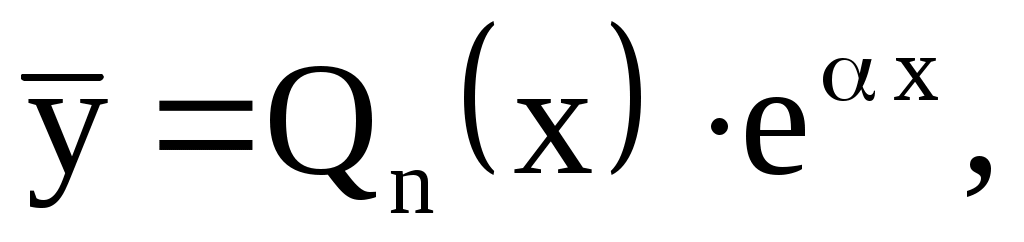
где 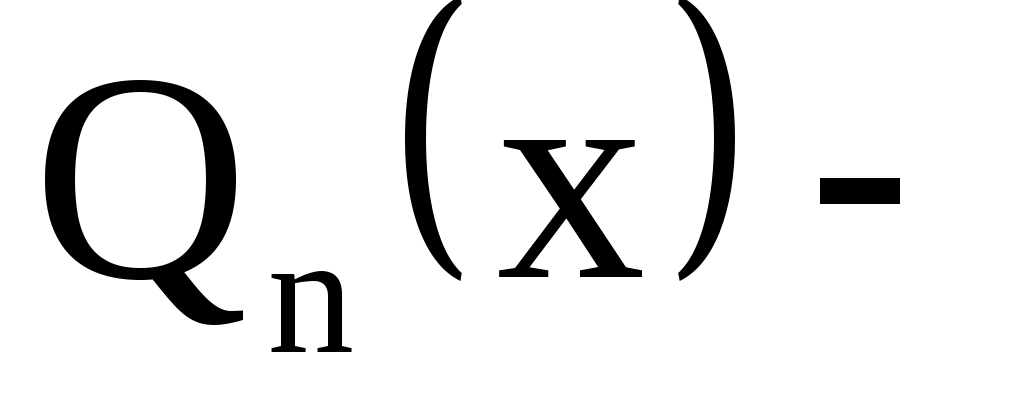 многочлен той же степени, что и данный многочлен многочлен той же степени, что и данный многочлен 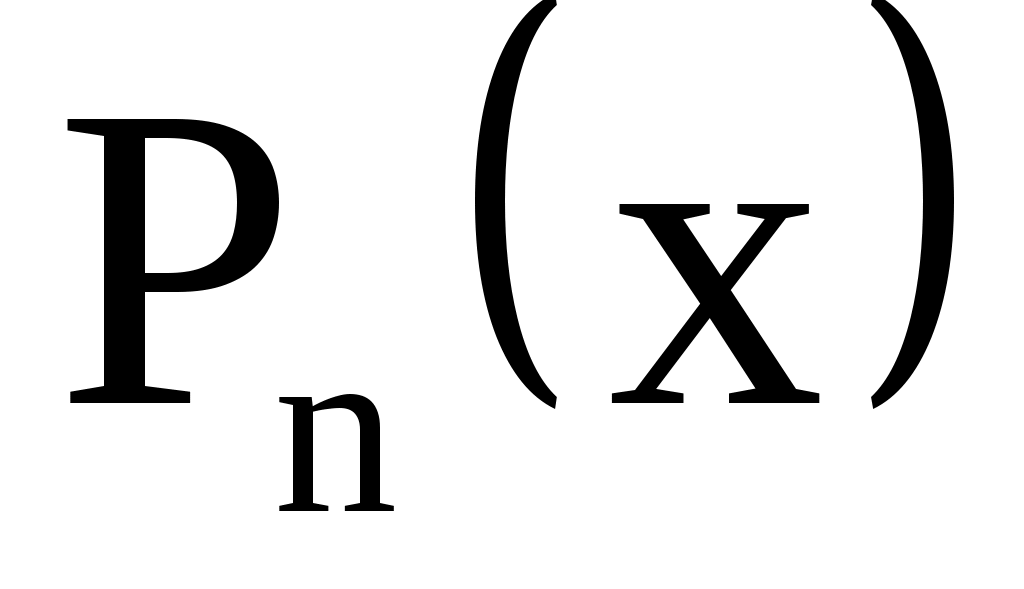 , но с неопределенными коэффициентами. , но с неопределенными коэффициентами.
Число 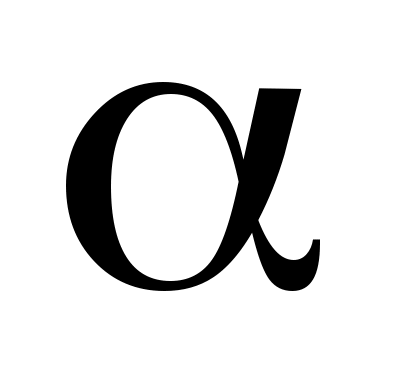 есть простой (однократный) корень характеристического уравнения (т. е. есть простой (однократный) корень характеристического уравнения (т. е. 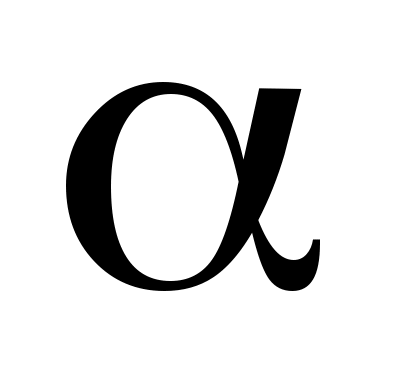 совпадает с одним корнем характеристического уравнения). В этом случае частное решение нужно искать в виде совпадает с одним корнем характеристического уравнения). В этом случае частное решение нужно искать в виде 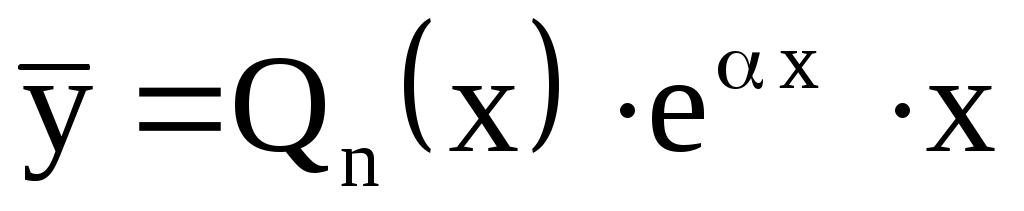 . .
Число 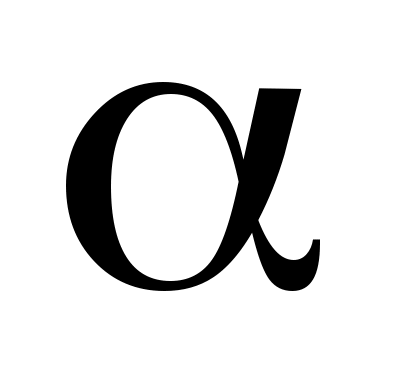 есть двукратный корень характеристического уравнения (т. е. есть двукратный корень характеристического уравнения (т. е. 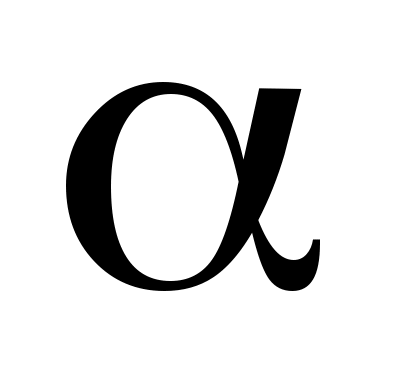 совпадает с двумя равными корнями характеристического уравнения). В этом случае частное решение нужно искать в виде совпадает с двумя равными корнями характеристического уравнения). В этом случае частное решение нужно искать в виде 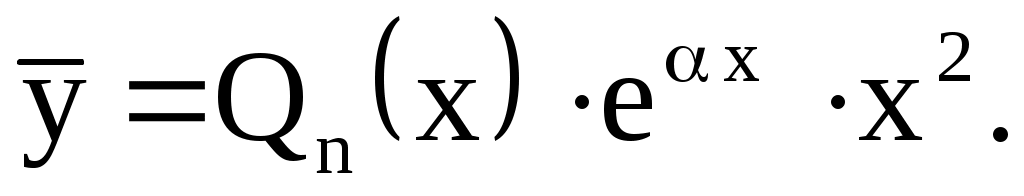 Неизвестные (неопределенные) коэффициенты многочлена Неизвестные (неопределенные) коэффициенты многочлена 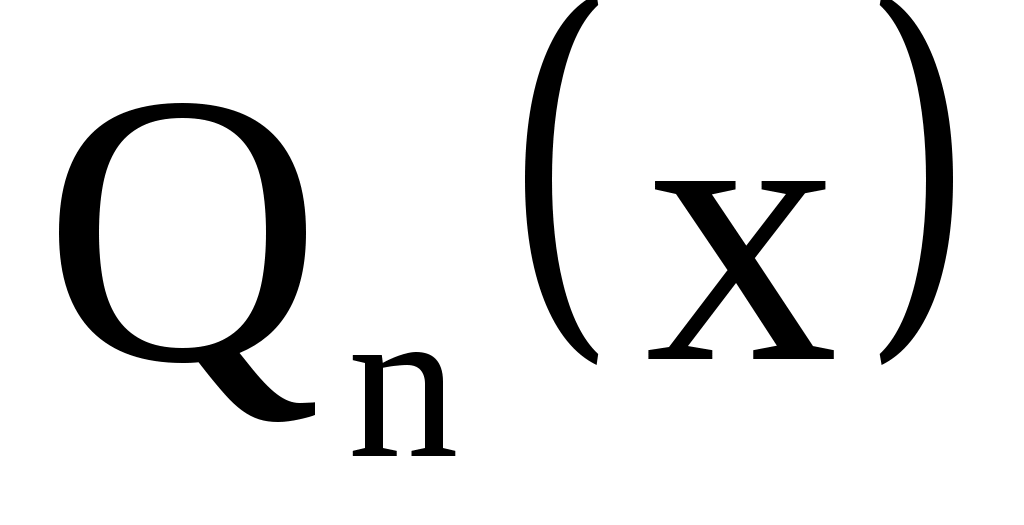 находим из условия, что функция находим из условия, что функция  является решением уравнения (13), т. е. удовлетворяет этому уравнению. является решением уравнения (13), т. е. удовлетворяет этому уравнению.
Рассмотрим примеры, на которых покажем не только принцип применения метода, но и порядок оформления решения.
№ 1. Найти общее решение уравнения
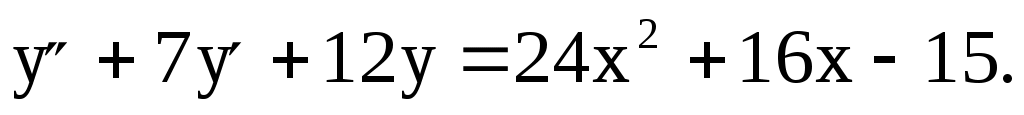
1) Составим характеристическое уравнение и найдем его корни:
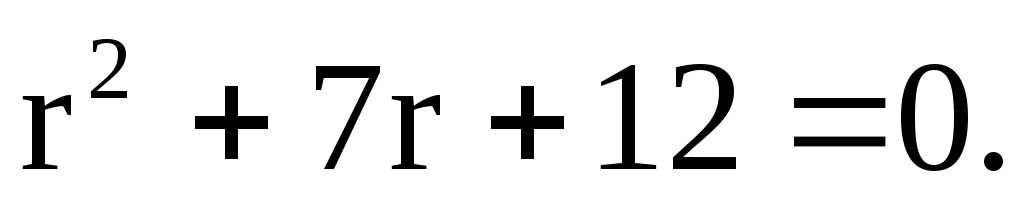
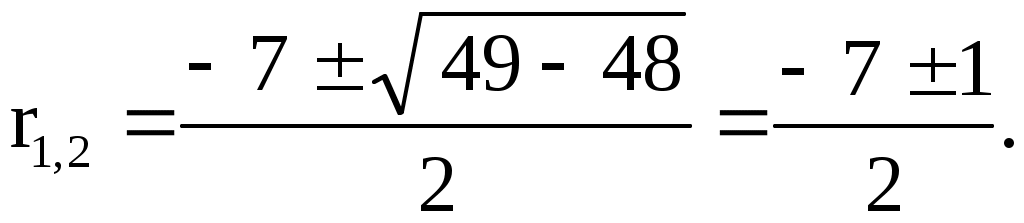

2) Запишем общее решение соответствующего однородного дифференциального уравнения:
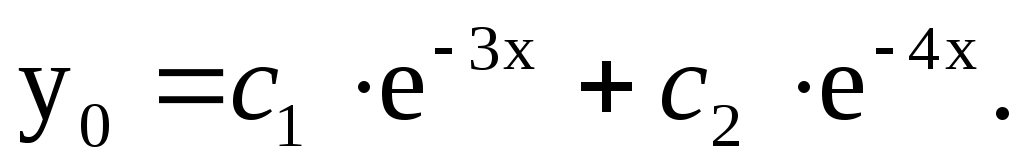
3) Запишем формулу, по которой следует искать частное решение  данного уравнения. Для этого сравним правую часть уравнения данного уравнения. Для этого сравним правую часть уравнения 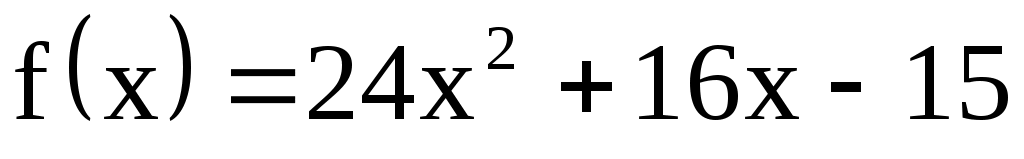
с общим видом правой части:
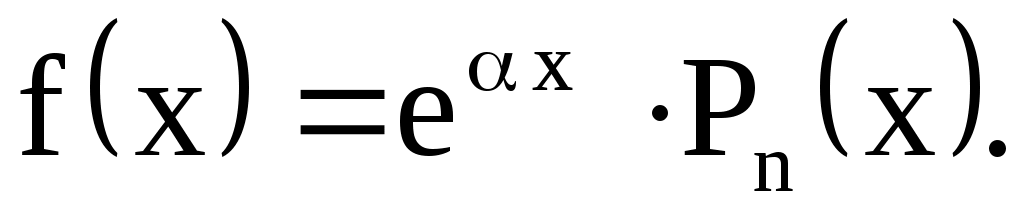
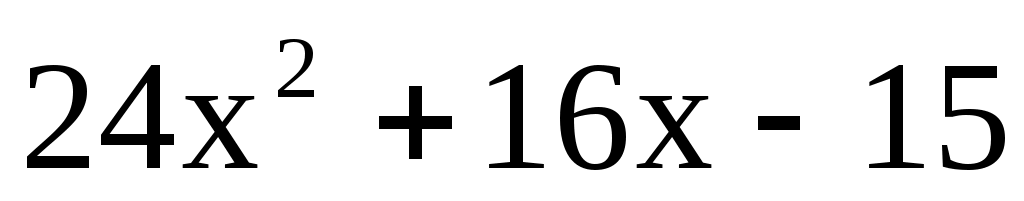 – многочлен второй степени с коэффициентами 24; 16; –15. – многочлен второй степени с коэффициентами 24; 16; –15.
В данном случае показательная функция 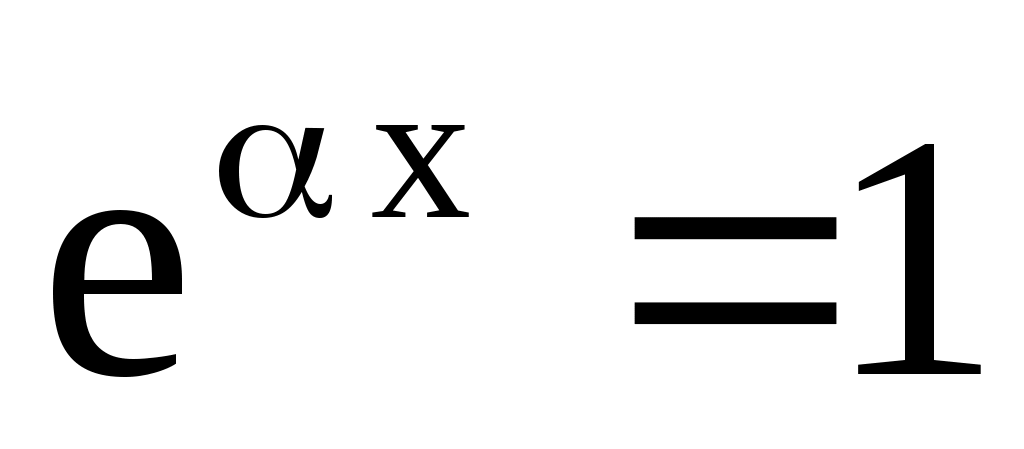 , т. е. , т. е. 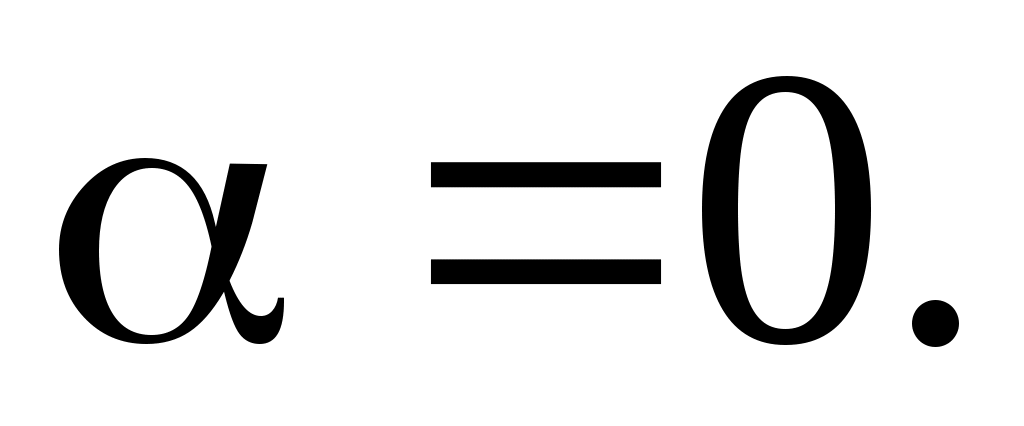 Так как Так как 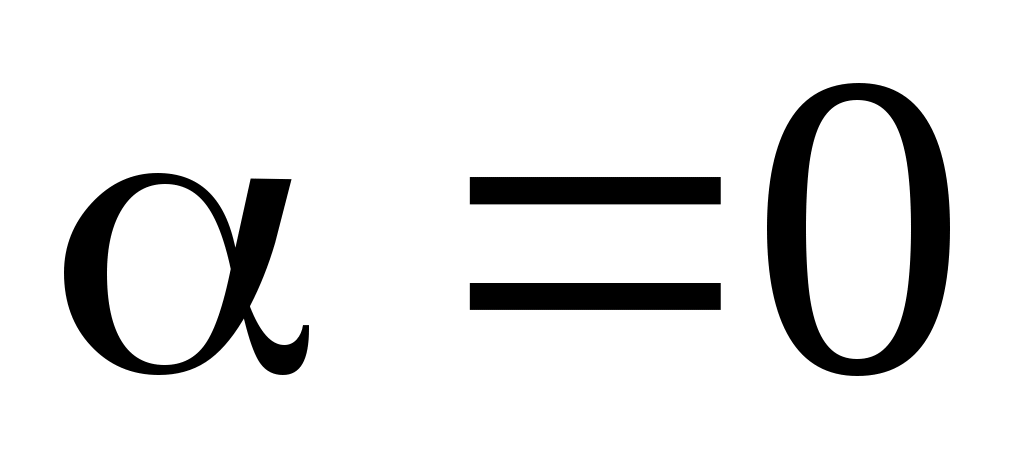 не совпадает ни с одним из корней характеристического уравнения не совпадает ни с одним из корней характеристического уравнения 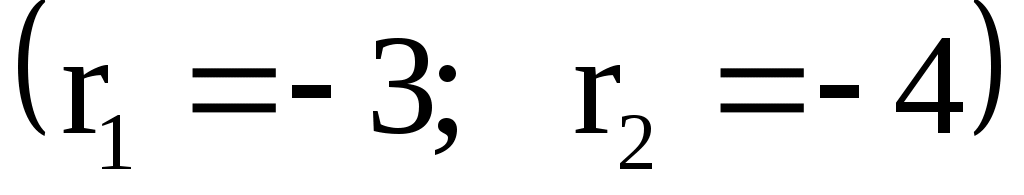 , частное решение нужно искать в виде , частное решение нужно искать в виде 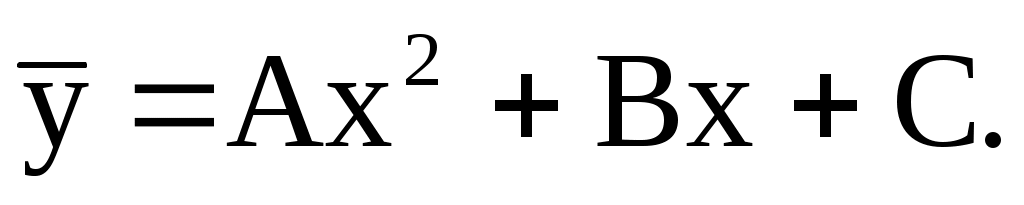
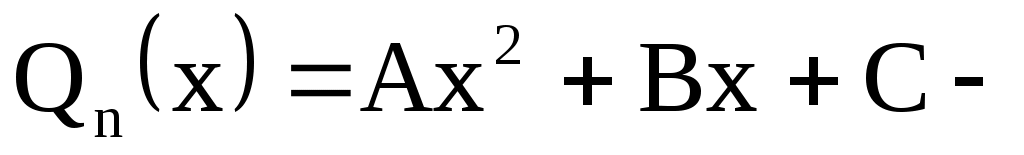 многочлен второй степени многочлен второй степени 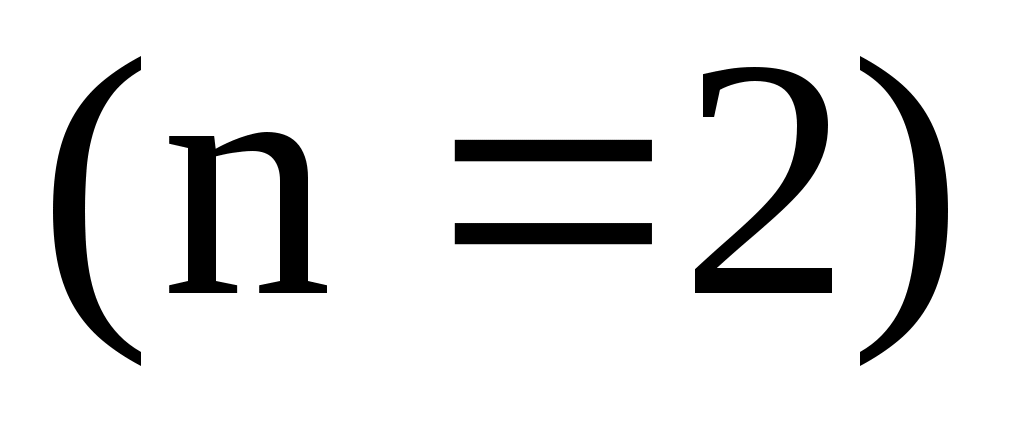 , неизвестные (неопределенные) коэффициенты А, В, С этого многочлена нужно найти, подставив выражения , неизвестные (неопределенные) коэффициенты А, В, С этого многочлена нужно найти, подставив выражения 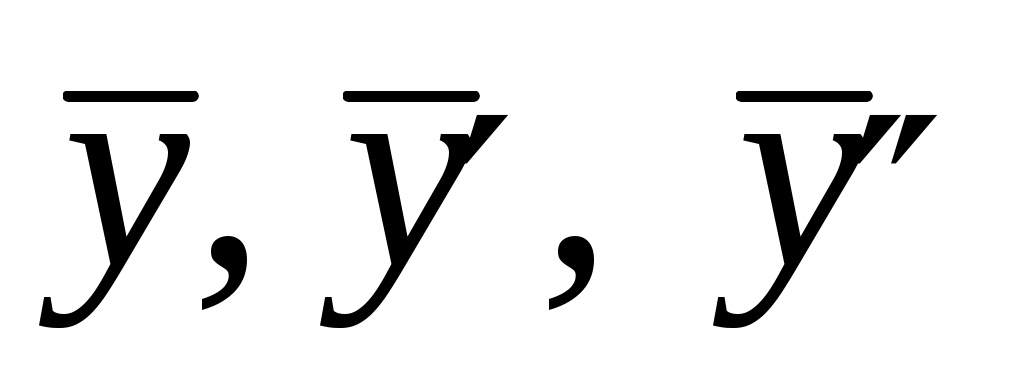 в данное уравнение. в данное уравнение.
4) Запишем 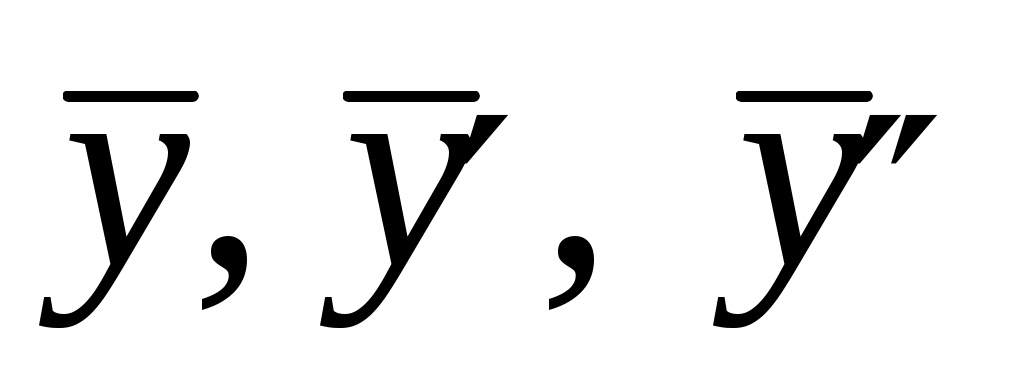 столбиком: столбиком:
 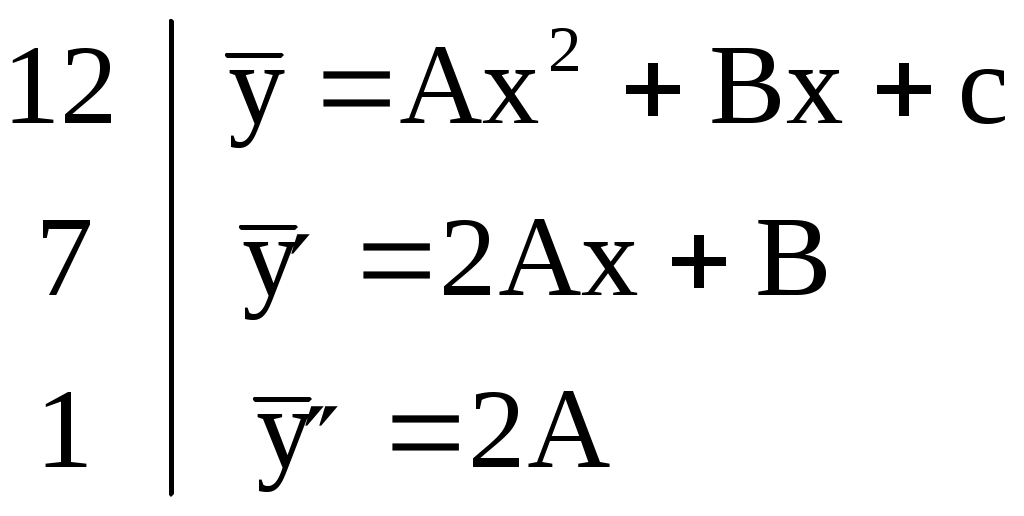
Слева указаны коэффициенты 12, 7, 1, на которые следует умножить 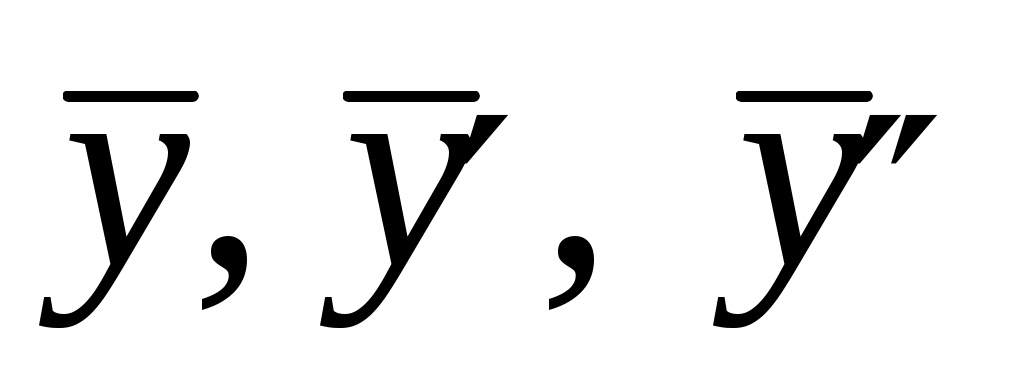 , чтобы получить левую часть уравнения , чтобы получить левую часть уравнения 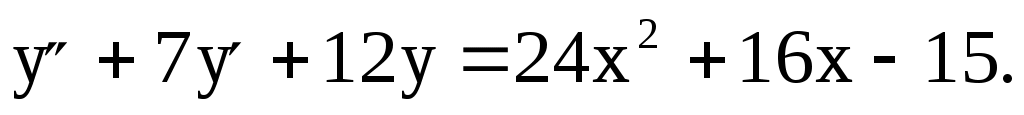 В левой части получим многочлен второй степени с неопределенными коэффициентами, который должен быть равен данному многочлену второй степени в правой части. Два многочлена будут равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях х. Запишем столбиком полученные уравнения: В левой части получим многочлен второй степени с неопределенными коэффициентами, который должен быть равен данному многочлену второй степени в правой части. Два многочлена будут равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях х. Запишем столбиком полученные уравнения:
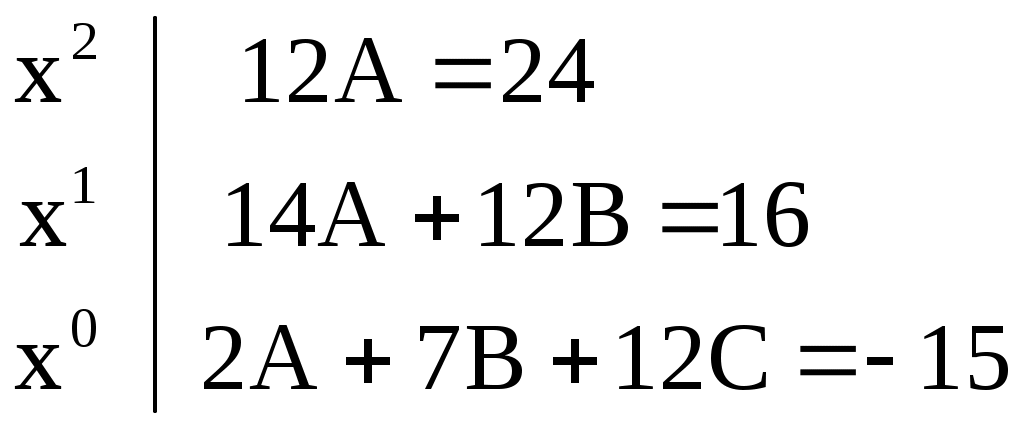  . .
Получили систему трех уравнений с тремя неизвестными коэффициентами
А, В, С. Решив ее, найдем 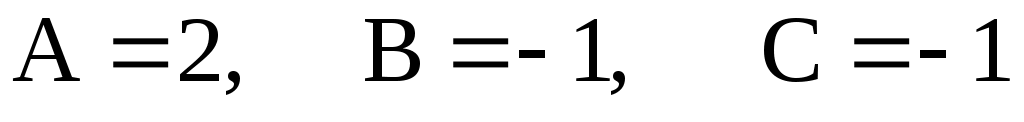 . .
Частное решение: 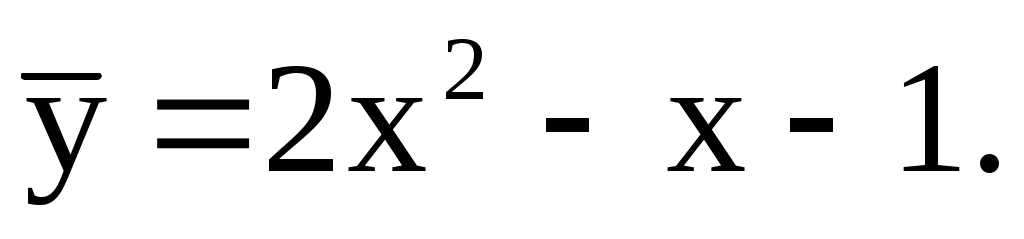
5). Общее решение данного уравнения:
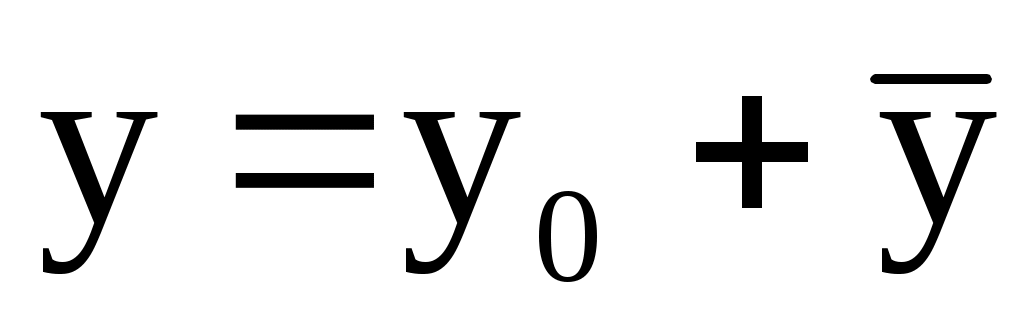
или
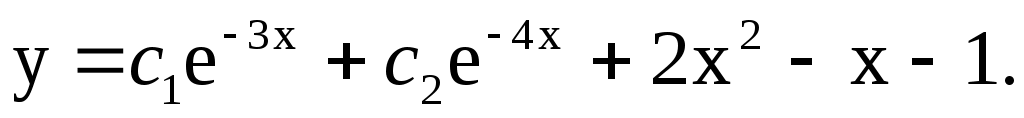
№ 2. Найти общее решение уравнения 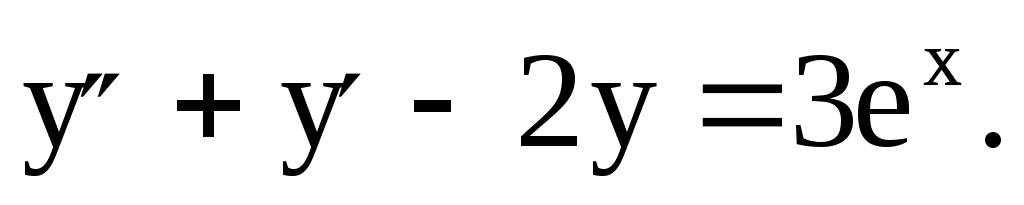
1) 
2) 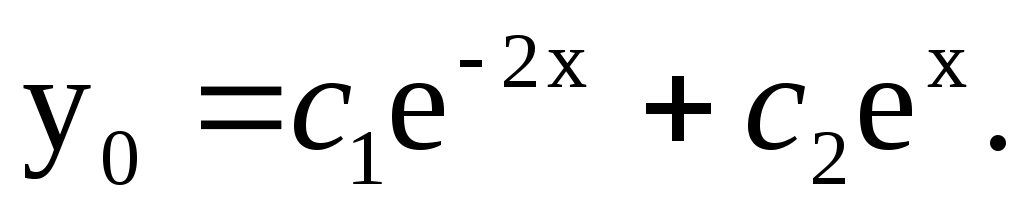
3) Сравним правую часть данного дифференциального уравнения 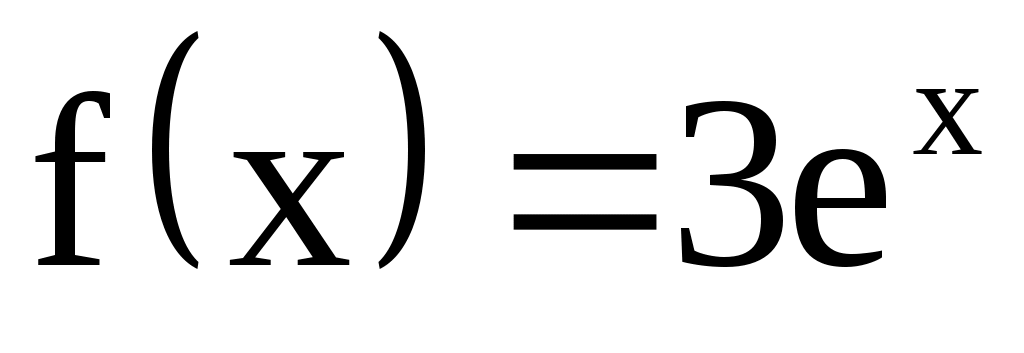 с с 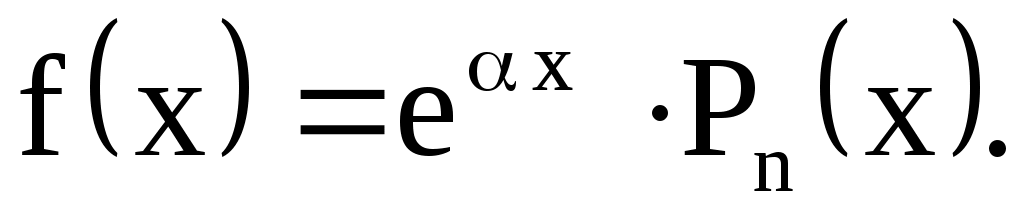 Отметим, что Отметим, что 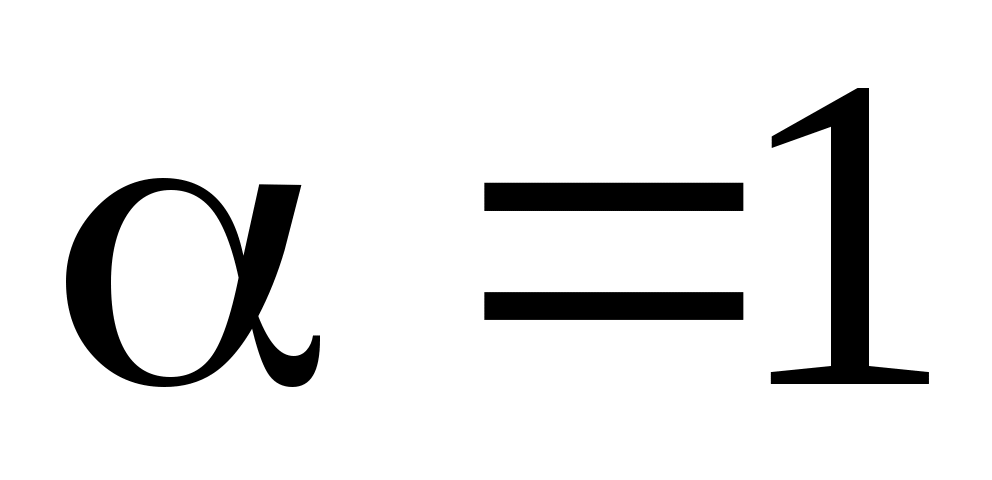 совпадает с одним корнем характеристического уравнения; многочлен – число 3 – нулевой степени, т. е. совпадает с одним корнем характеристического уравнения; многочлен – число 3 – нулевой степени, т. е. 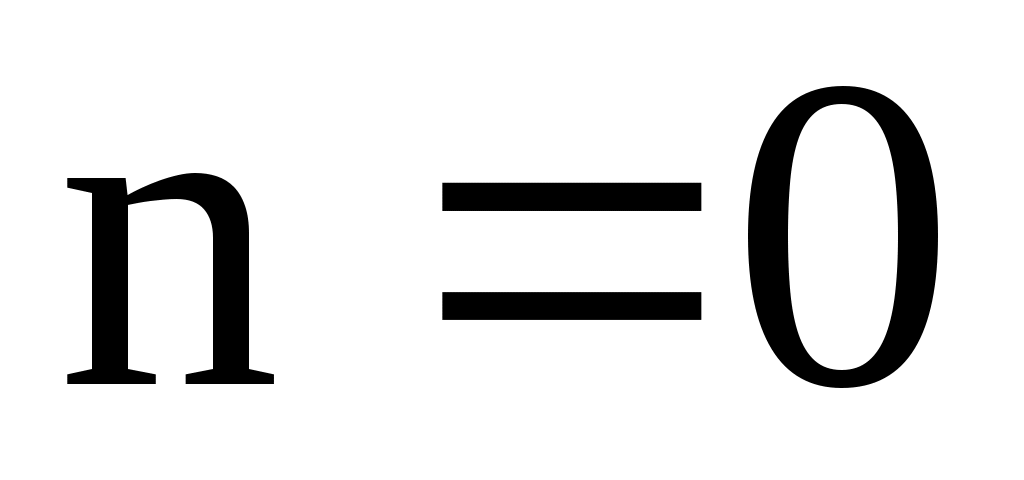 . Поэтому частное решение . Поэтому частное решение 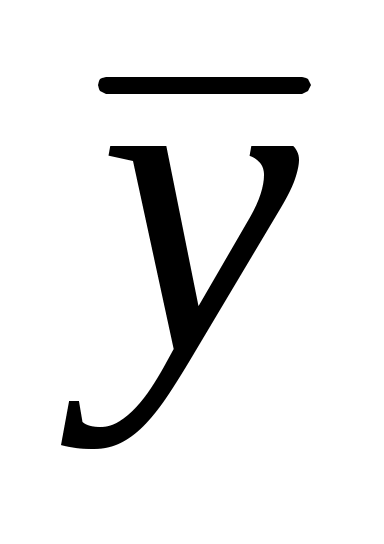 следует искать в виде следует искать в виде 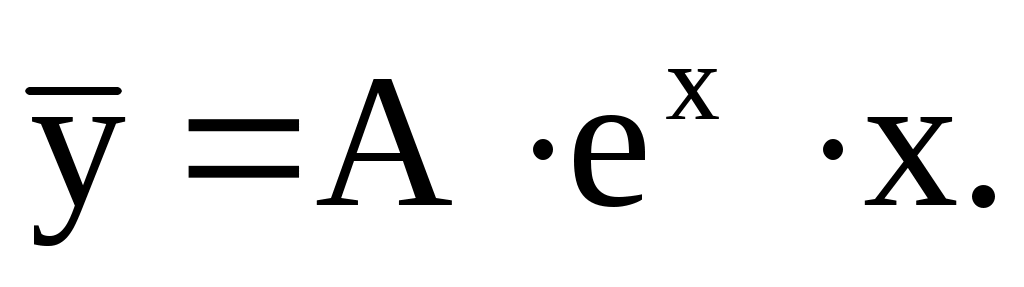
4) Запишем
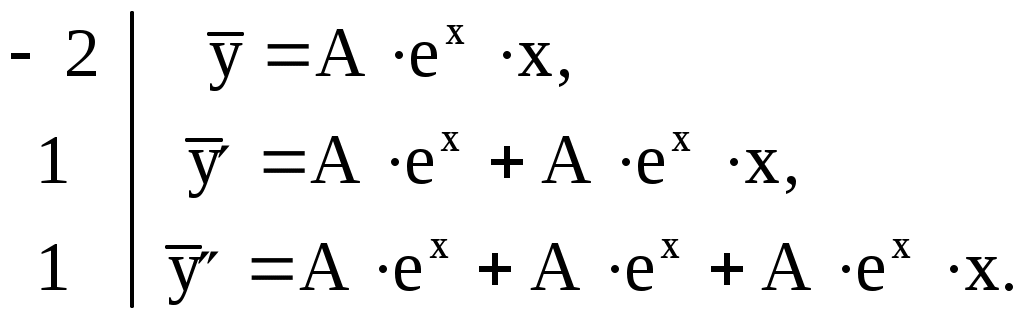
Подставив выражения 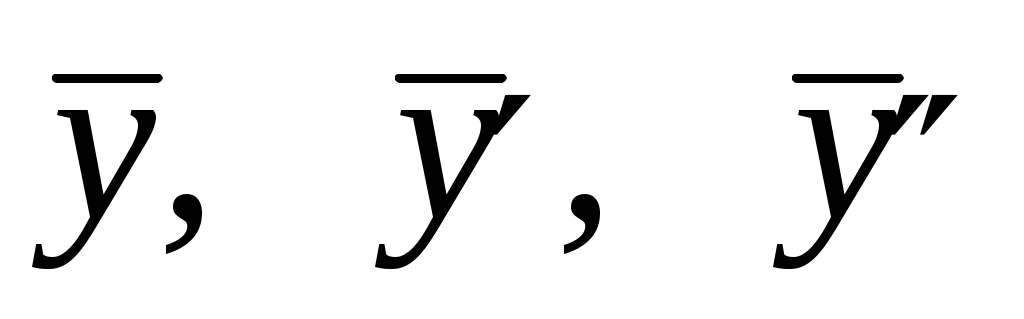 с указанными коэффициентами в данное дифференциальное уравнение, получим с указанными коэффициентами в данное дифференциальное уравнение, получим
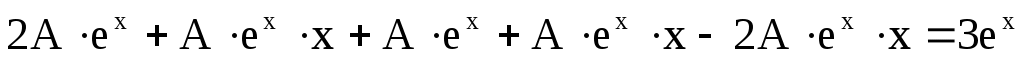
или
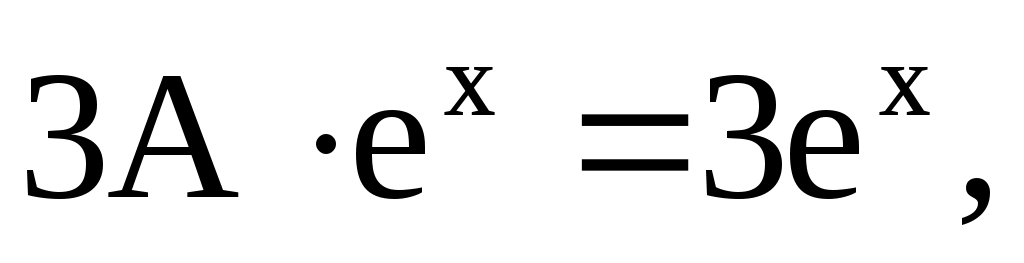
откуда 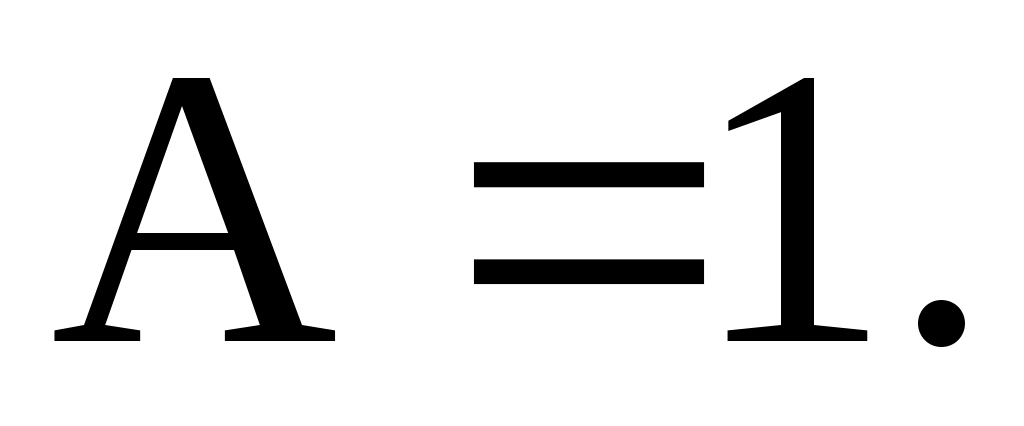 Частное решение: Частное решение: 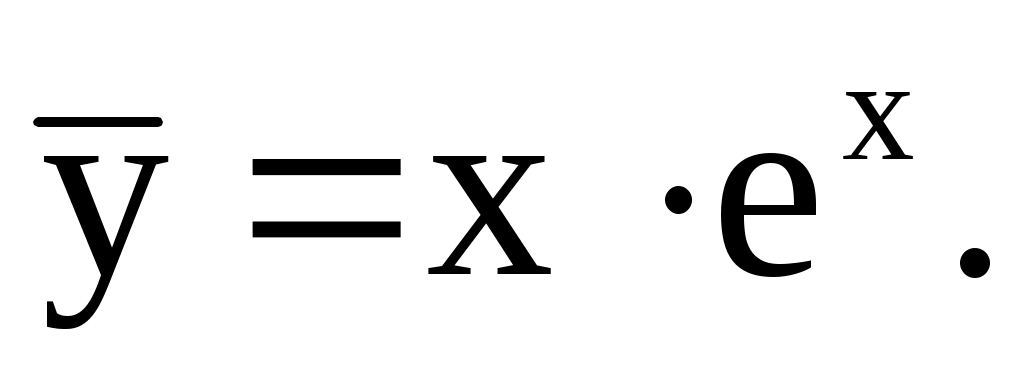
5) Искомое общее решение данного уравнения:
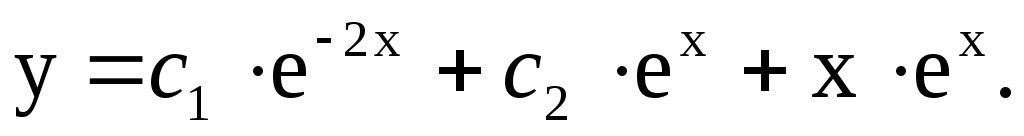
№ 3. 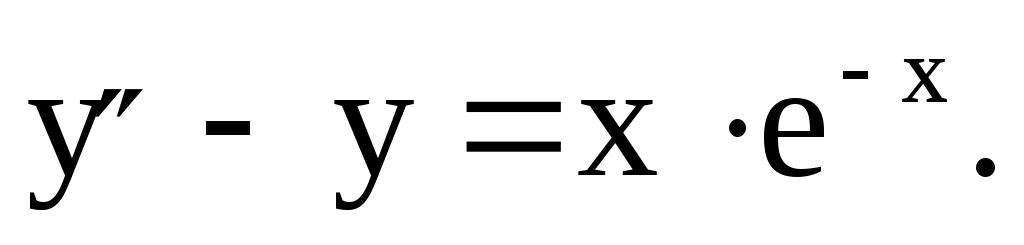
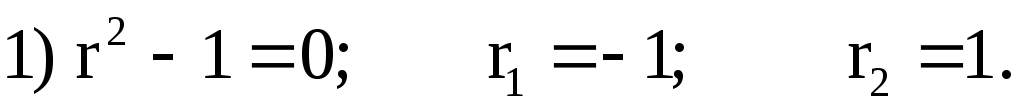
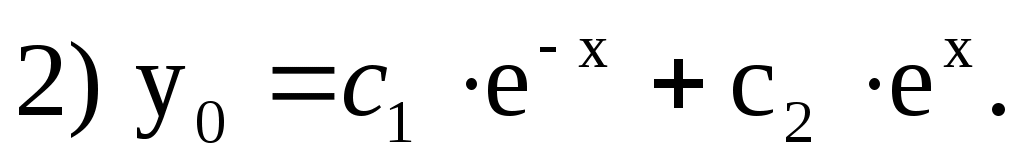
3) Сравним правую часть данного уравнения 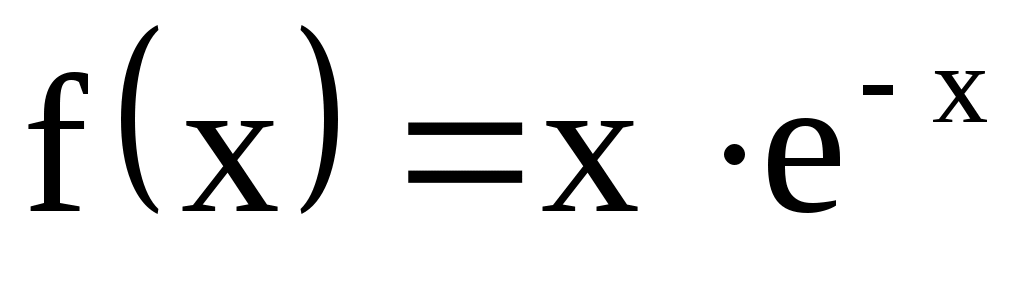 с с 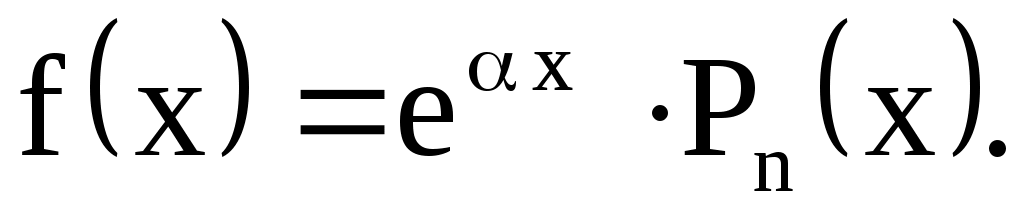
Отмечаем, что 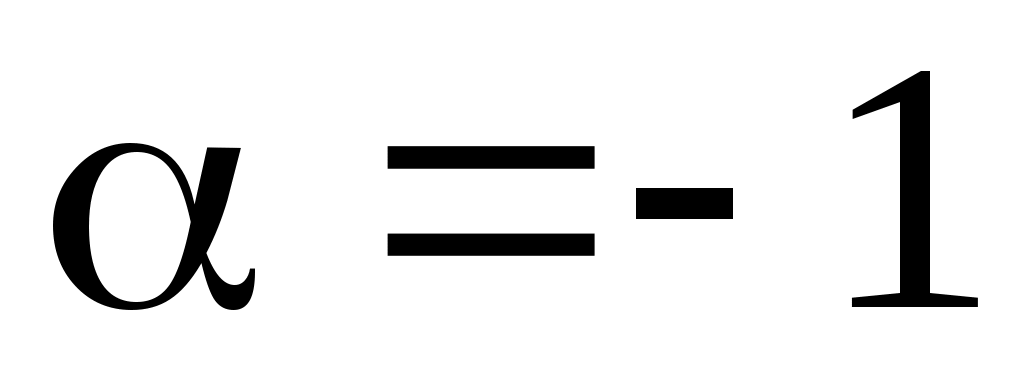 совпадает с одним корнем характеристического уравнения и многочлен х степени совпадает с одним корнем характеристического уравнения и многочлен х степени 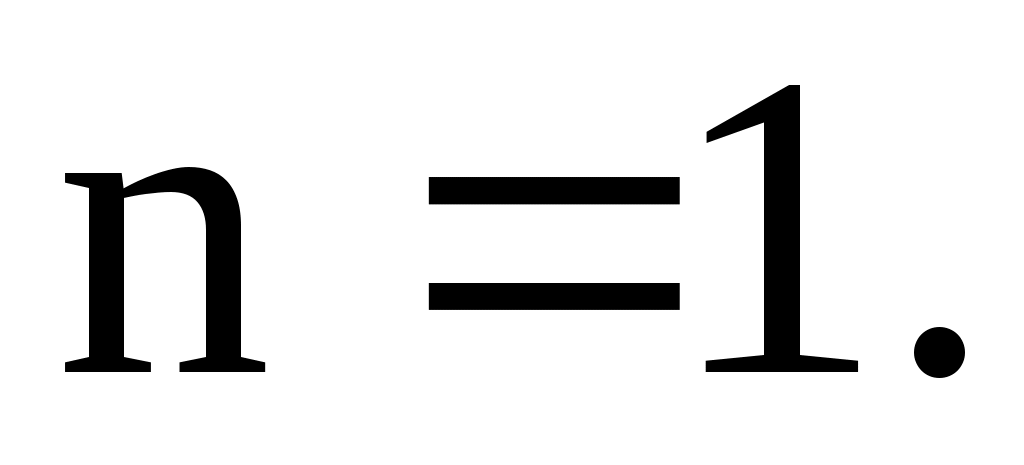 Поэтому частное решение следует искать в виде Поэтому частное решение следует искать в виде
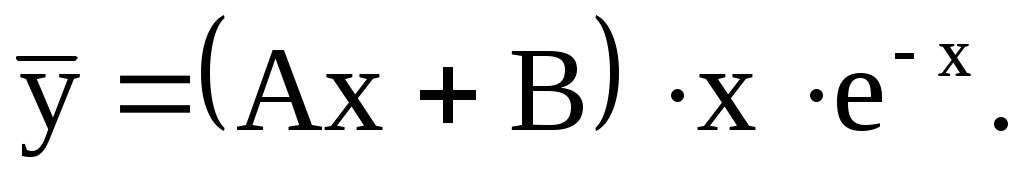
4) Так как требуется найти 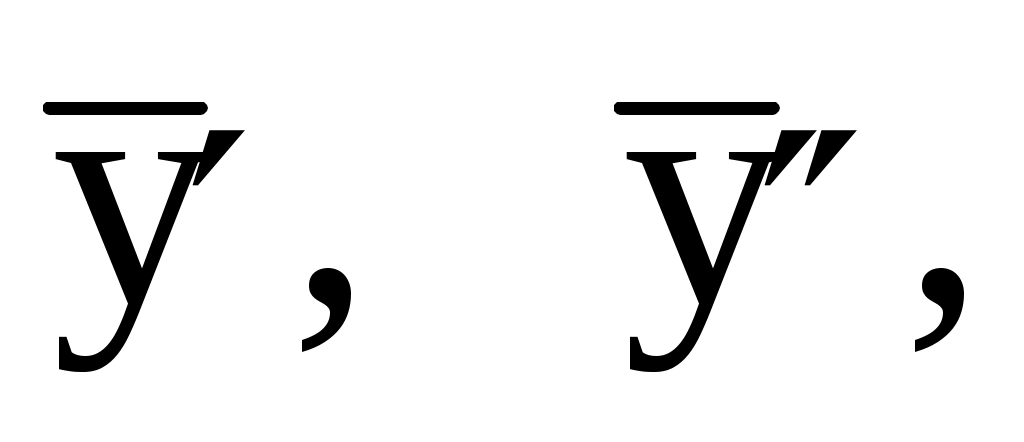 удобнее записать удобнее записать 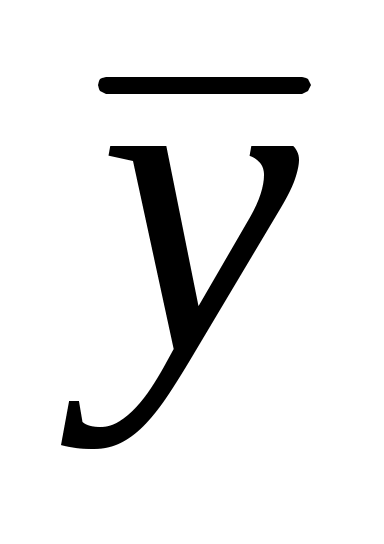 в виде в виде
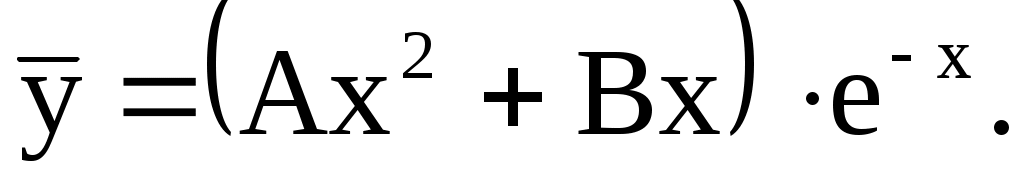
Запишем 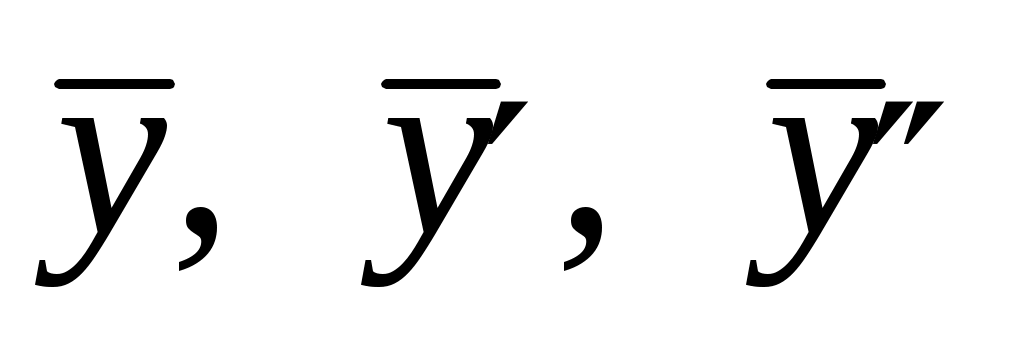 столбиком: столбиком:
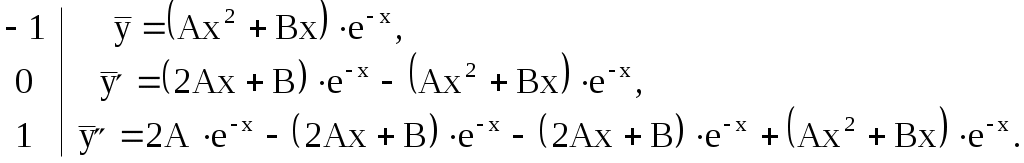
Подставим выражения 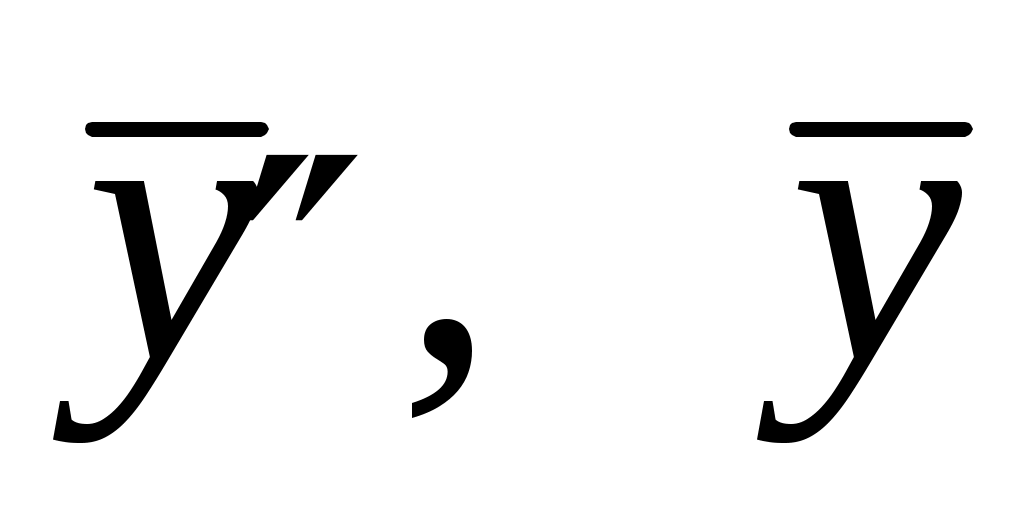 с указанными коэффициентами в данное уравнение. Получим равенство с указанными коэффициентами в данное уравнение. Получим равенство
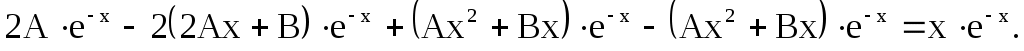
Разделим уравнение на 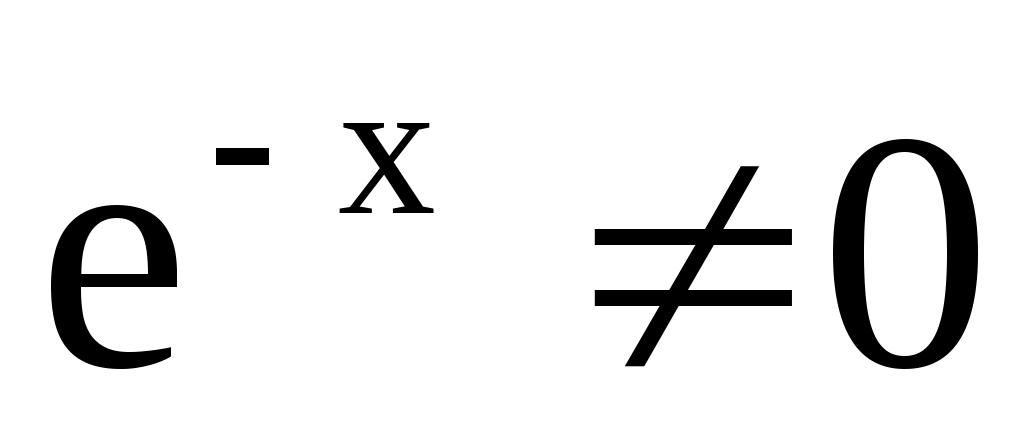 и упростим: и упростим:
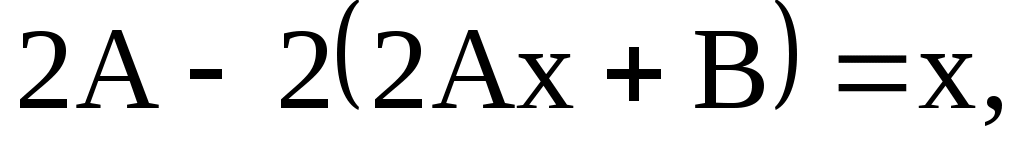
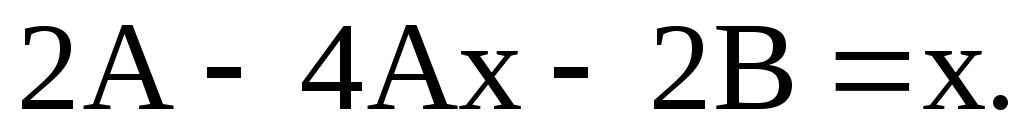
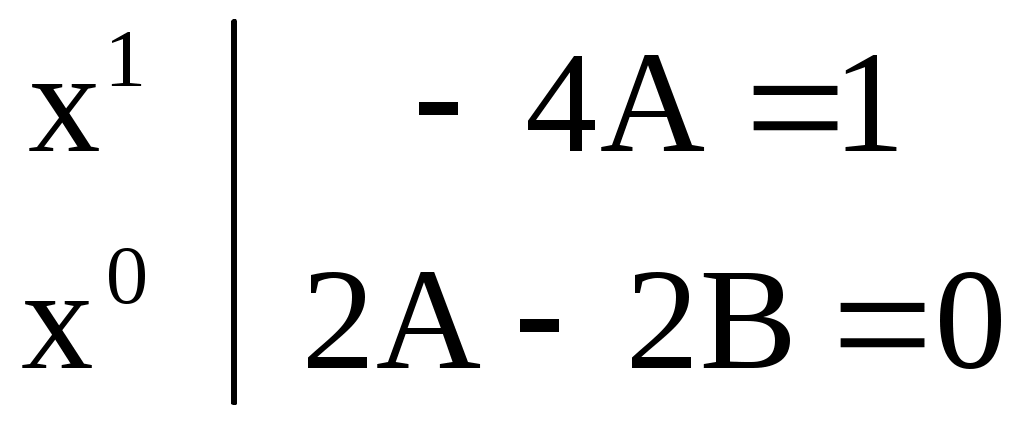  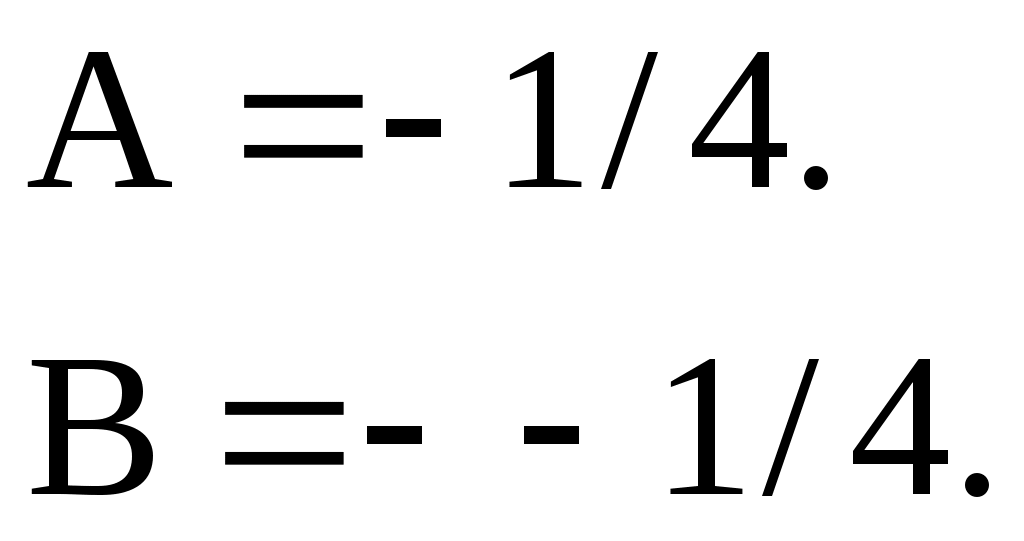
Частное решение: 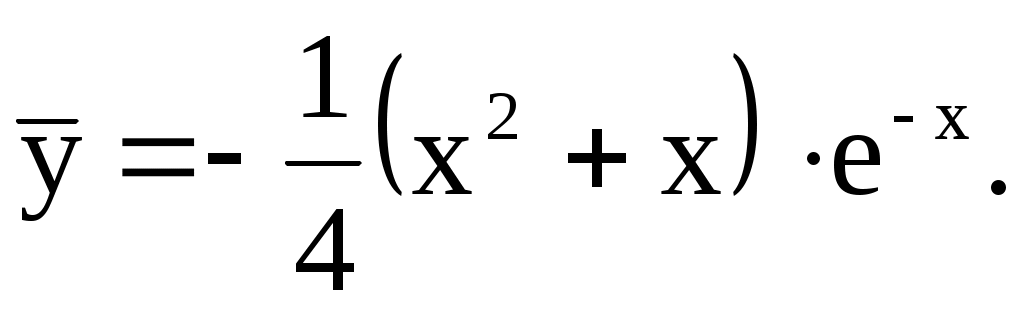
Общее решение дифференциального уравнения:
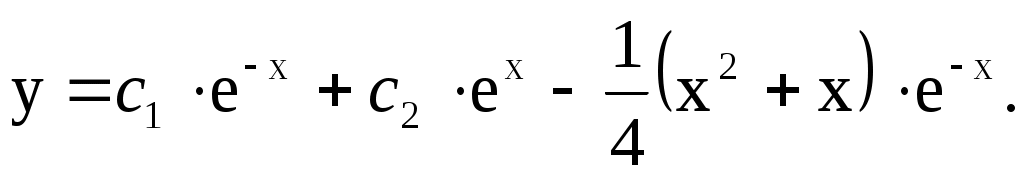
Пусть правая часть 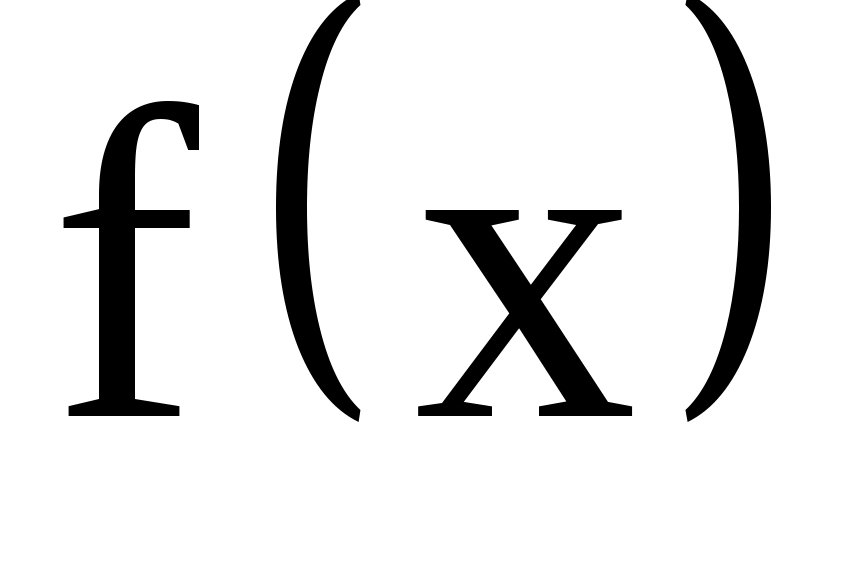 уравнения (13) уравнения (13)
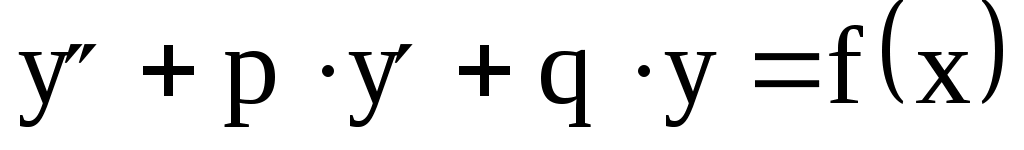
имеет вид
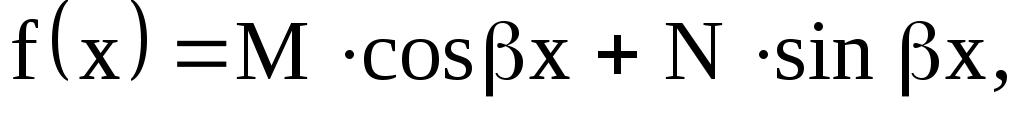
где 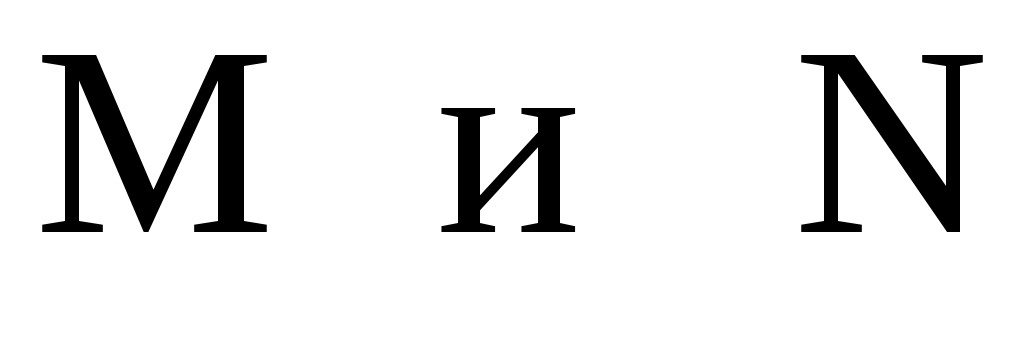 – постоянные числа. Тогда вид частного решения – постоянные числа. Тогда вид частного решения 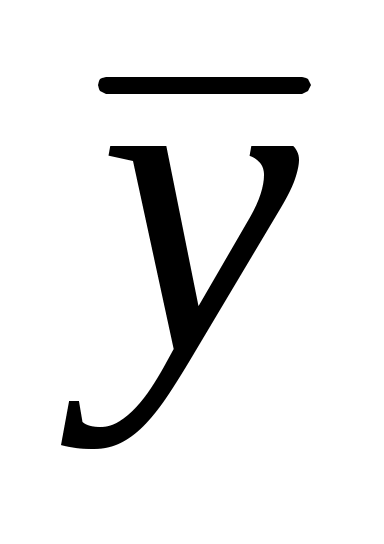 определяется следующим образом. определяется следующим образом.
а) Если число  не есть корень характеристического уравнения (16), то частное решение не есть корень характеристического уравнения (16), то частное решение 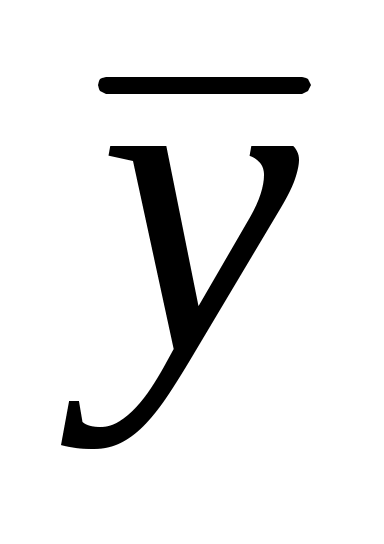 имеет вид имеет вид
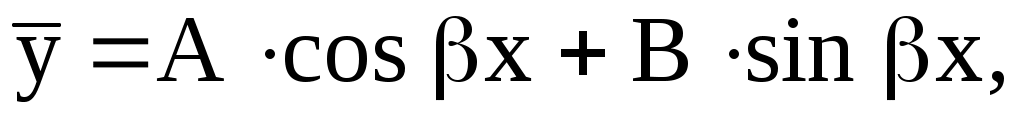
где А и В – постоянные неопределенные коэффициенты.
б) Если число  есть корень характеристического уравнения (16), то есть корень характеристического уравнения (16), то
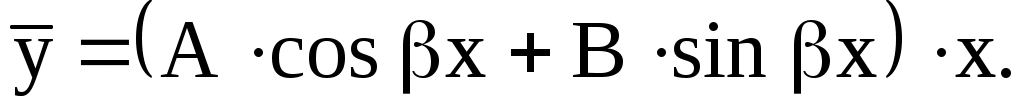
Сделаем важное замечание. Даже тогда, когда в правой части уравнения стоит выражение, содержащее только 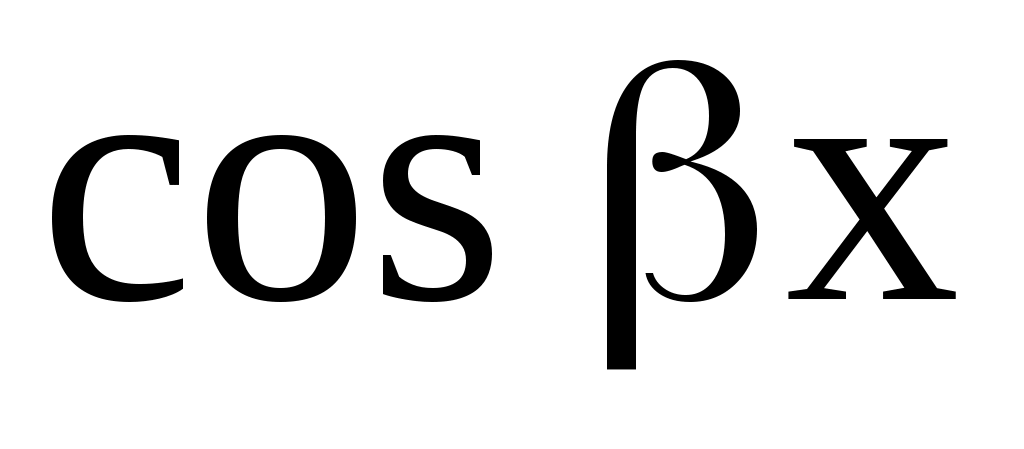 или только или только 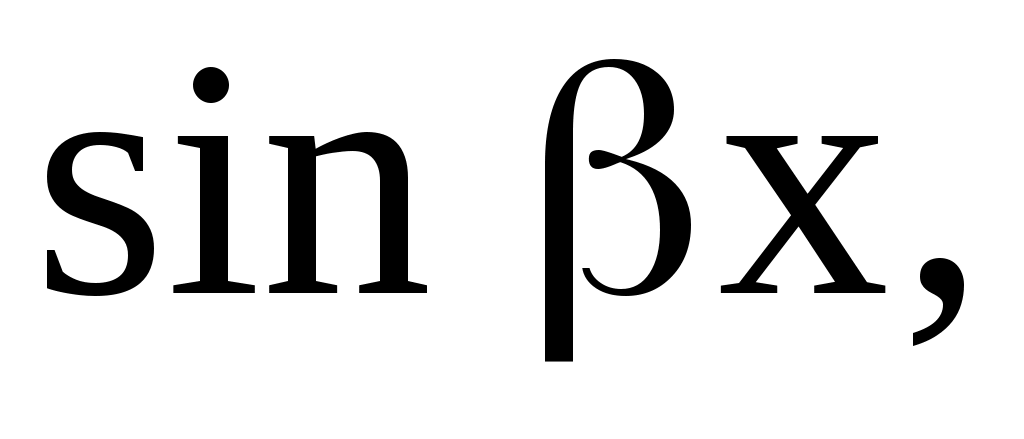 следует искать частное решение в том виде, в каком оно было указано, т. е. с синусом и косинусом. Иными словами, из того, что правая часть не содержит следует искать частное решение в том виде, в каком оно было указано, т. е. с синусом и косинусом. Иными словами, из того, что правая часть не содержит 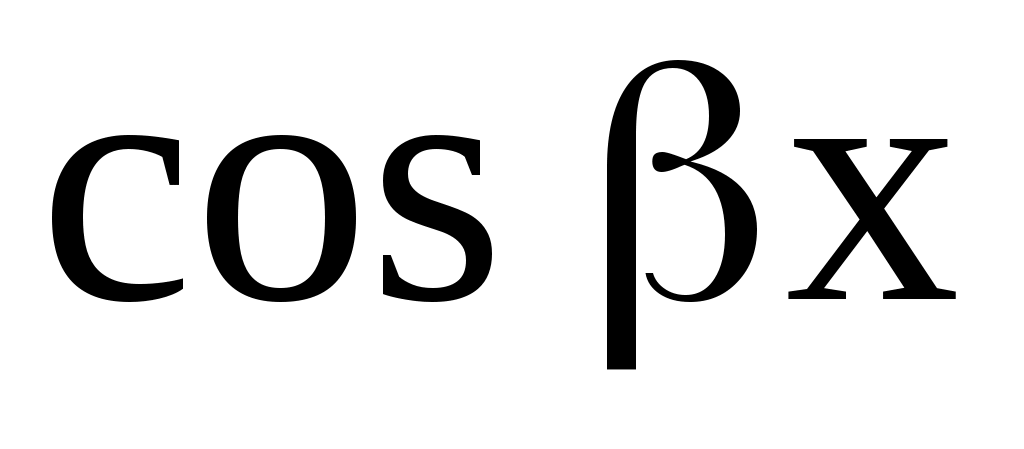 или или 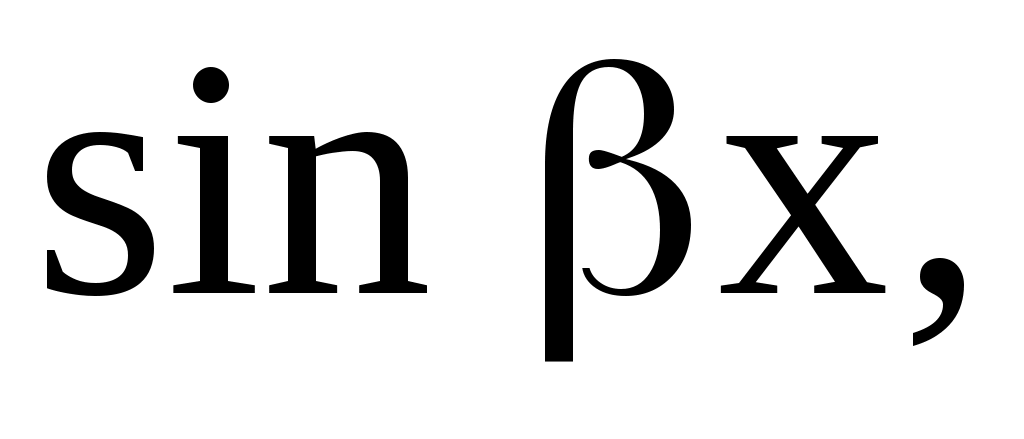 не следует, что частное решение уравнения не содержит этих функций. не следует, что частное решение уравнения не содержит этих функций.
Пример № 1. Решить уравнение
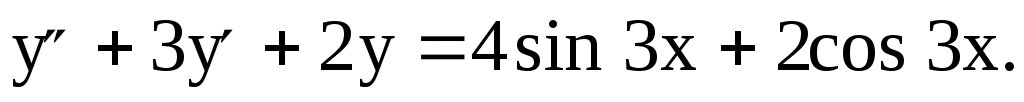
1) 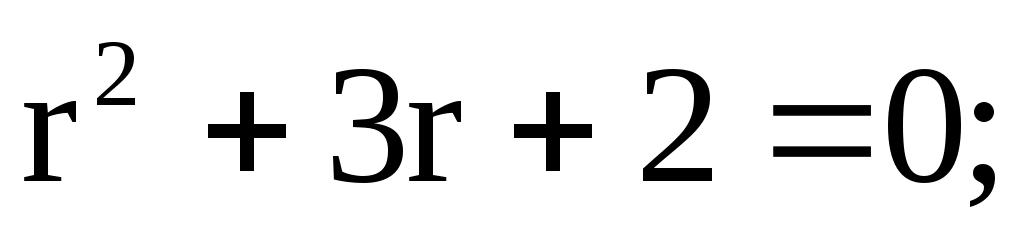
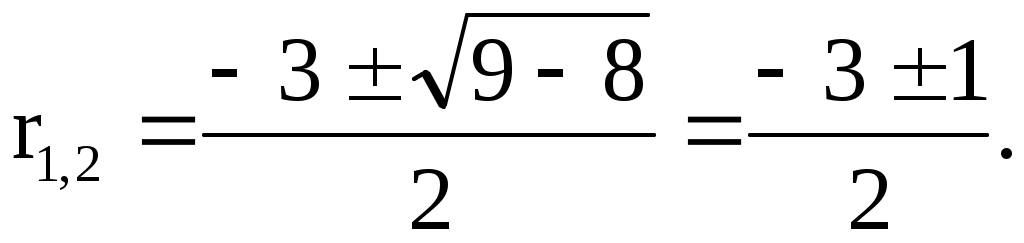

2) 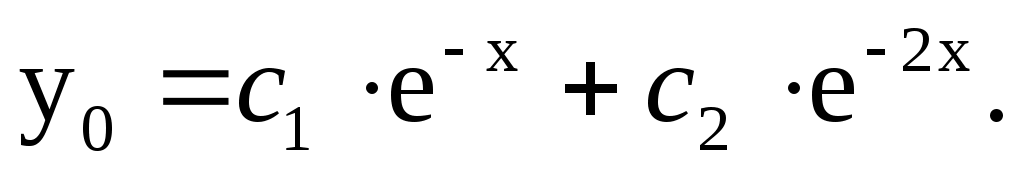
3) Сравним правую часть уравнения 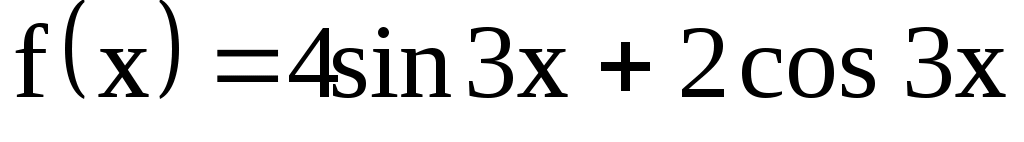 с с 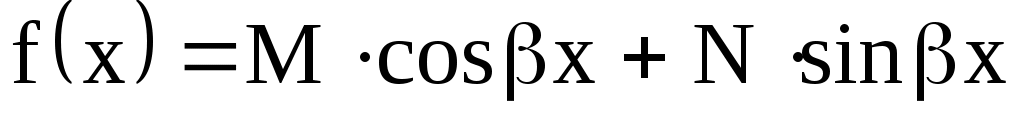 . Здесь . Здесь 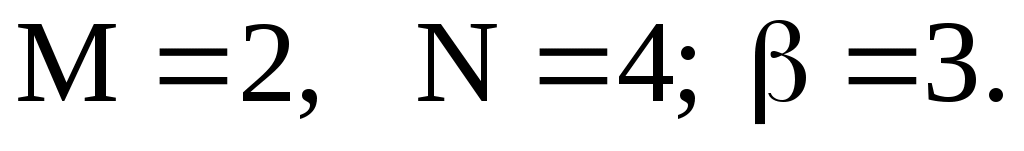 Так как числа Так как числа 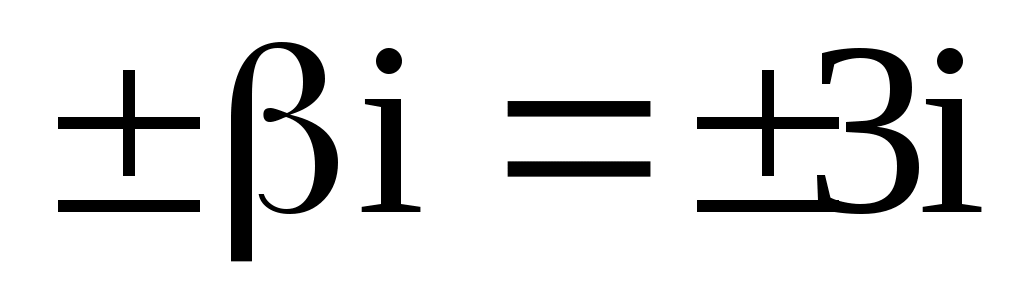 не являются корнями характеристического уравнения, частное решение следует искать в виде не являются корнями характеристического уравнения, частное решение следует искать в виде 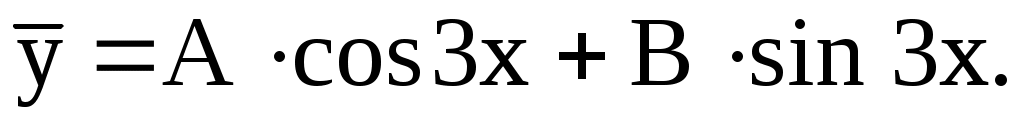
4) Найдем 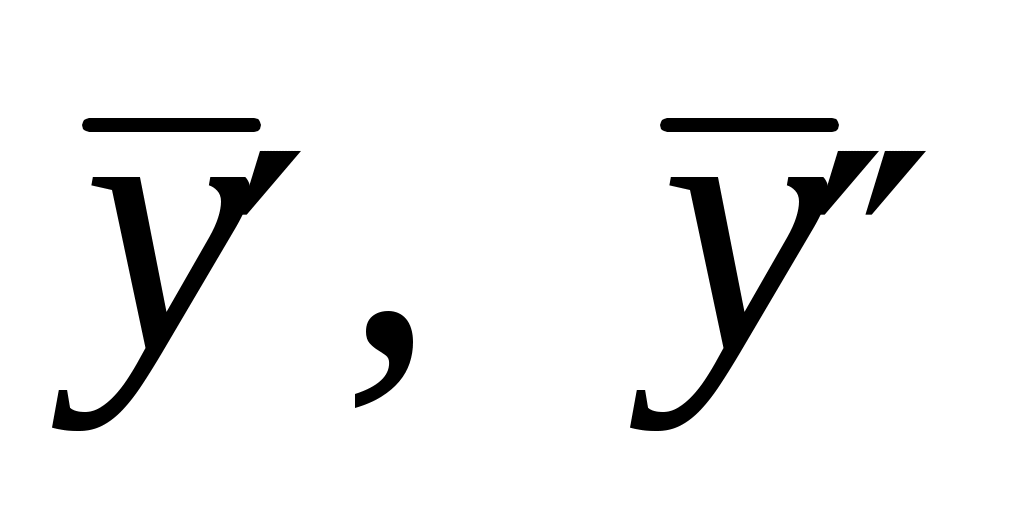 и запишем столбиком и запишем столбиком
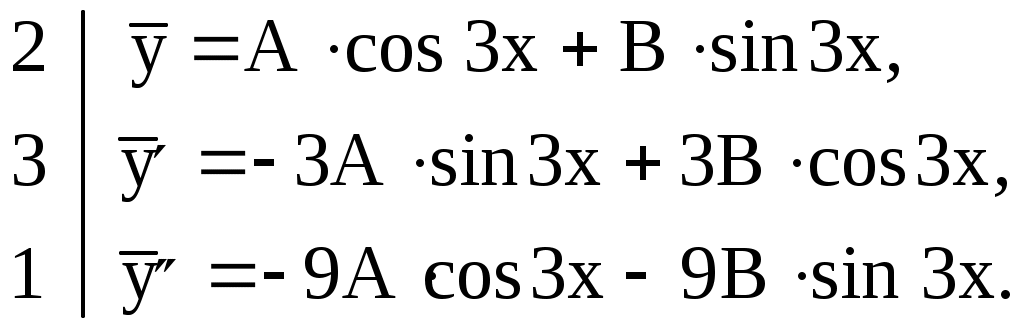
Подставив эти выражения в данное дифференциальное уравнение, получим
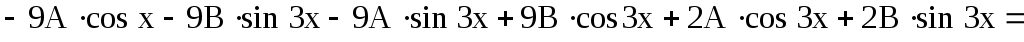
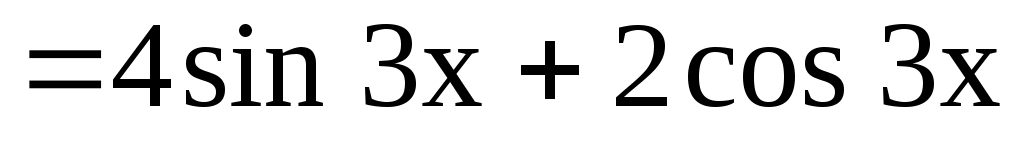
или 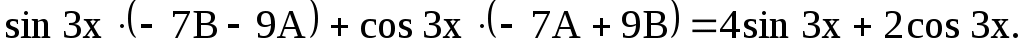
Приравниваем коэффициенты при 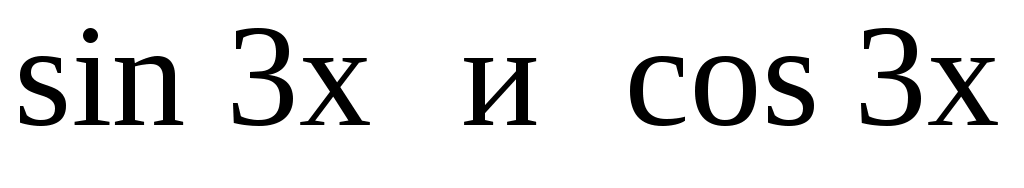 в левой и правой частях уравнения, получим систему уравнений: в левой и правой частях уравнения, получим систему уравнений:
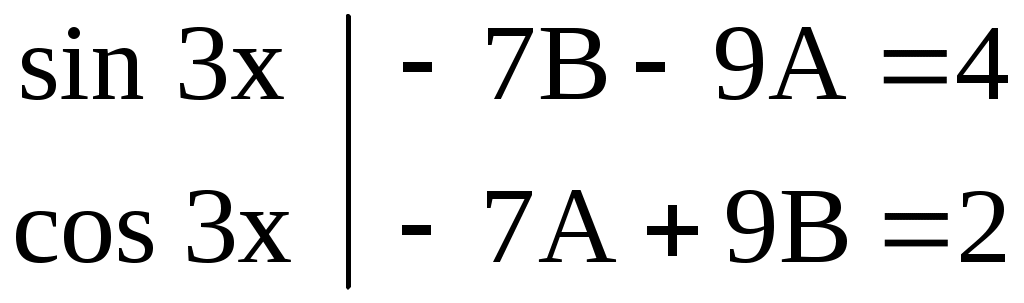 
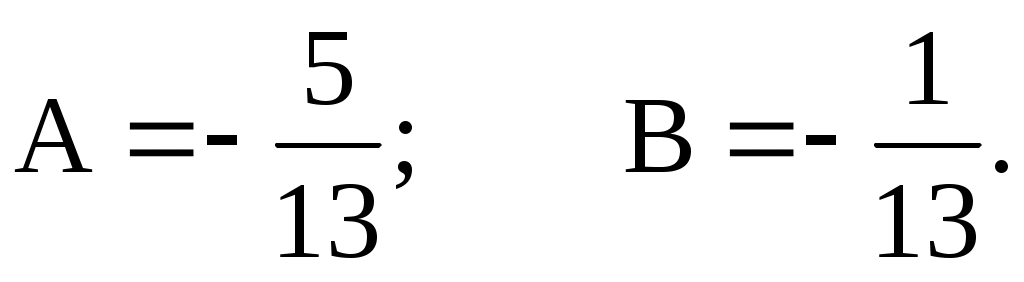
Частное решение: 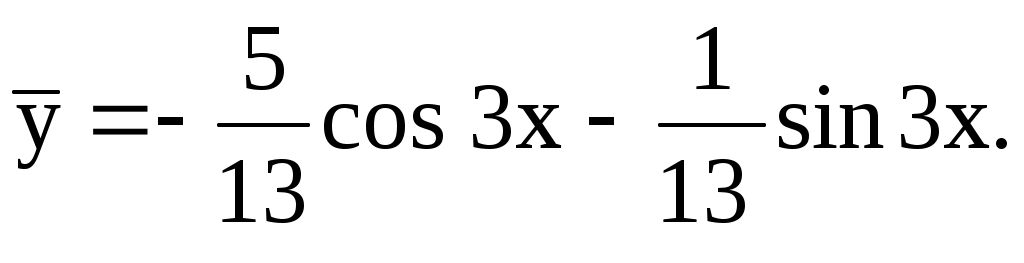
Общее решение данного дифференциального уравнения:
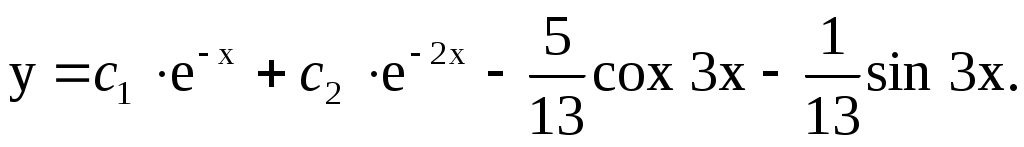 |
|
|
 Скачать 1.72 Mb.
Скачать 1.72 Mb.