10 ТЕМА. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. 10. обыкновенные дифференциальные уравнения содержание 1
 Скачать 1.72 Mb.
|
|
Четвертый шаг. Интегрируя почленно уравнение, получим общее решение исходного уравнения (или его общий интеграл).  Рассмотрим уравнения № 1.  № 2.  № 3.  Дифференциальное уравнение № 1 является дифференциальным уравнением с разделяющимися переменными, по определению. Разделим уравнение на произведение  Получим уравнение  Интегрируя, получим      или  Последнее соотношение есть общий интеграл данного дифференциального уравнения. В дифференциальном уравнении № 2 заменим  умножим на  , получим      общее решение дифференциального уравнения.Дифференциальное уравнение № 3 не является уравнением с разделяющимися переменными, т. к., записав его в виде  или  ,видим, что выражение  в виде произведения двух множителей (один – только с y, другой – только с х) представить невозможно. Заметим, что иногда нужно выполнить алгебраические преобразования, чтобы видеть, что данное дифференциальное уравнение – с разделяющимися переменными. Пример № 4. Дано уравнение  Преобразуем уравнение, вынося общий множитель слева   Разделим левую и правую части уравнения на произведение  получим Проинтегрируем обе части уравнения:    откуда  – общий интеграл данного уравнения. (а)Заметим, что если постоянную интегрирования записать в виде  , то общий интеграл данного уравнения может иметь другую форму:   или  – общий интеграл. (б)Таким образом, общий интеграл одного и того же дифференциального уравнения может иметь различную форму. Важно в любом случае доказать, что полученный общий интеграл удовлетворяет данному дифференциальному уравнению. Для этого нужно продифференцировать по х обе части равенства, задающего общий интеграл, учитывая, что y есть функция от х. После исключения с получим одинаковые дифференциальные уравнения (исходное). Если общий интеграл  , (вид (а)), то     Если общий интеграл  (вид (б)), то     Получим то же уравнение, что и в предыдущем случае (а). Рассмотрим теперь простые и важные классы уравнений первого порядка, приводящиеся к уравнениям с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка Легко можно убедиться в том, что дифференциальные уравнения  не являются уравнениями с разделяющимися переменными. Они являются Определение.'> однородными уравнениями. Определение. Дифференциальное уравнение  называется однородным дифференциальным уравнением первого порядка, если  – однородная функция нулевого измерения.Дадим понятие однородной функции нулевого измерения. Определение. Функция  называется однородной функцией нулевого измерения, если при любом t справедливо тождество  Так, функции   – однородные функции нулевого измерения, т. к.   Чтобы проверить, является ли д. у.1 однородным уравнением, нужно в этом уравнении заменить  Если после этого t всюду сократится и получится первоначальное уравнение, то данное уравнение – однородное.Поэтому уравнение  является однородным. Действительно, сократив уравнение на t, получим исходное уравнение.Решение однородного дифференциального уравнения первого порядка Так как функция в правой части уравнения  является однородной функцией нулевого измерения, то, по определению,  Положим в этом тождестве  получим  т. е. однородная функция нулевого измерения зависит только от отношения у/х. Д.у.1 в этом случае примет вид Сделаем подстановку y/x=u, т. е.  где  неизвестная функция.Тогда  Уравнение  примет вид  или  или  – уравнение с разделяющимися переменными. Интегрируя, находим  Найдя отсюда выражение u как функции от x, подставим его в равенство  получим искомое общее решение однородного д.у. 1. Чаще всего не уда-ется найти явное выражение функции  Тогда после интегрирования следует в левую часть вместо u подставить  В результате получим общий интеграл (т. е. общее решение в неявном виде).Решим уравнения. Пример 1. Найти общее решение дифференциального уравнения  Решаем уравнение подстановкой  Подставив  в данное уравнение, получим  или  Получили дифференциальное уравнение с разделяющимися переменными относительно вспомогательной функции  Упростим правую часть: Умножив на  , получим уравнение с разделенными переменными  Интегрируя, получим  или  или  Потенцируем  Подставив  получим о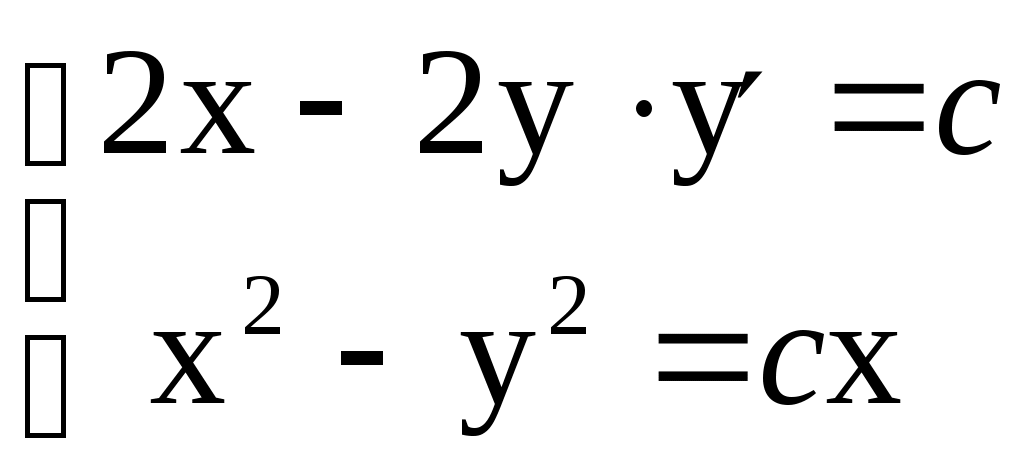бщий интеграл данного дифференциального уравнения.  Проверка:   или  – искомое уравнение.Пример 2. Найти частное решение дифференциального уравнения  при начальных условиях  Убедимся, что данное дифференциальное уравнение является однородным. Подставим в уравнение вместо  соответственно  Получим   Разделив на t обе части уравнения, получим данное уравнение. Решаем уравнение подстановкой  Поставим  в уравнение, получим  Сгруппируем слагаемые с  . – это уравнение с разделяющимися переменными. Разделив обе части на  получим  – уравнение с разделенными переменными. Интегрируя левую и правую части уравнения, получим Подставив  получим общий интеграл данного дифференциального уравнения: Найдем частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям  Подставим в формулу общего интеграла   отсюда  и частный интеграл Линейные дифференциальные уравнения первого порядка Определение. Линейным уравнением первого порядка называется уравнение, линейное относительно искомой функции и ее производной. Общий вид линейного д.у.1:  непрерывные функции или постоянные. Если  , то уравнение  решается как дифференциальное уравнение с разделяющимися переменными. Рассмотрим уравнения: 1)  Это уравнение является линейным по определению , но лучше рассматривать его как уравнение с разделяющимися переменными: 2)  Это уравнение не является линейным, т. к. функция y в уравнении имеет не первую степень, а выше3)  Уравнение является линейным по определению. Но проще рассматривать его как однородное д.у.1:  где  – однородная функция нулевого измерения.4)  Запишем уравнение в виде  . Это линейное д.у.1. |