10 ТЕМА. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. 10. обыкновенные дифференциальные уравнения содержание 1
 Скачать 1.72 Mb.
|
|
Пример. Составить линейное однородное д.у.II, зная характеристическое уравнение  Д.у. II будет таким:  Решение квадратных уравнений Обратимся к решению квадратных уравнений  Формула корней квадратного уравнения:  где  – дискриминант. Любое квадратное уравнение всегда имеет два корня (это известное положение высшей алгебры).Если  имеютместо два различных действительных корня. Если  Имеем два равных действительных корня.3) Если  то квадратное уравнение имеют два корня, но они не являются действительными числами. Эти корни называются комплексными числами. Обозначим  назовем мнимой единицей  Тогда число вида  где  действительные числа, называется комплексным числом. Здесь  называется действительной частью,  мнимой частью комплексного числа. Для всякого комплексного числа  существует комплексное число, ему сопряженное:  Так, для числа  сопряженным является число  Два комплексных числа  и  являются взаимно сопряженными. Покажем примеры решения квадратных уравнений.№ 1.     различные действительные корни.№ 2.    различные действительные корни.№ 3.    равные действительные корни.№ 4.  – различные корни.№ 5.    Уравнение имеет два комплексных корня, взаимно сопряженных, c действительной частью  и коэффициентом мнимой части  № 6.    Уравнение имеет 2 взаимно сопряженных комплексных корня:  где Заметим, что всякое алгебраическое уравнение степени n имеет ровно n корней, среди которых могут быть как действительные (различные или равные), так и комплексные (обязательно попарно взаимно сопряженные). № 7.  Разложим левую часть уравнения на множители:   Нужно решить три простейших уравнения: Имеем четыре корня:  Решение однородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами Дано дифференциальное уравнение  При решении характеристического уравнения  возможны три случая.1) Корни характеристического уравнения (16) действительны и различны:  В этом случае частными решениями  будут функции ;  при этом эти решения линейно независимы, т. к.  Тогда по теореме 1 общее решение уравнения (14) имеет вид  (17)где  произвольные постоянные.2) Корни характеристического уравнения (16) действительны и равны:  (обозначим их  ). Тогда имеет место одно частное решение д.у. II  Доказано, что второе частное решение имеет вид  при этом очевидно, что эти решения линейно независимы. Тогда общим решением д.у. II будет или  (18)3) Корни характеристического уравнения (16) комплексные сопряженные:  Тогда общее решение д.у. II имеет вид  . (19)Рассмотрим примеры. № 1.    – характеристическое уравнение.  По формуле (17) находим общее решение дифференциального уравнения:  № 2.   – характеристическое уравнение.  По формуле (18) получим общее решение дифференциального уравнения:  № 3.   –характеристическое уравнение. Уравнение имеет комплексные корни  По формуле (19) общим решением будет  или  № 4. Найти частное решение уравнения  при начальных условиях  Характеристическое уравнение:   Общее решение –  Найдем производную  Подставив начальные условия 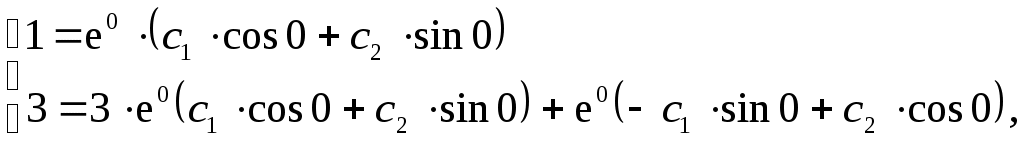 получим систему для определения   или 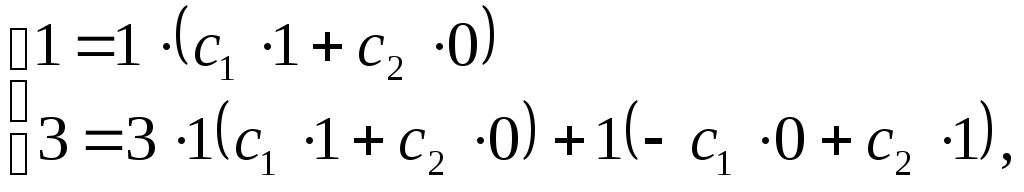 или 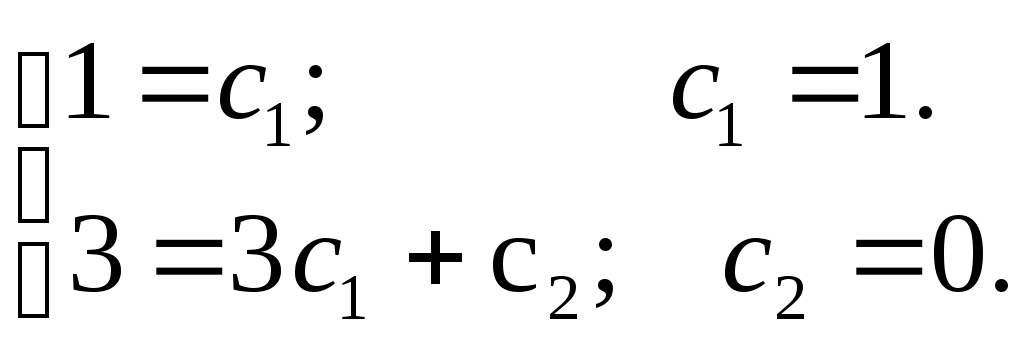 Подставив полученные значения  в общее решение, получим  – искомое частное решение.Проверка. Найдем первую  и вторую  производные функции и подставим в данное дифференциальное уравнение:     –верное равенство, т. е. частное решение найдено верно.Таким образом, решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами совершается без операции интегрирования функций (как в случае д.у.1) и полностью завершается посредством решения алгебраических квадратных уравнений. Аналогичный результат имеет место и для линейных однородных д.у. с постоянными коэффициентами высших порядков. Примеры решения однородных линейных дифференциальных уравнений высших порядков № 1.   – характеристическое уравнение    Общее решение:  или  № 2.   – характеристическое уравнение.   Общее решение:  или  .№ 3.      Общее решение:  № 4.   – характеристическое уравнение.Положим       Общее решение уравнения:  |