10 ТЕМА. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. 10. обыкновенные дифференциальные уравнения содержание 1
 Скачать 1.72 Mb.
|
|
Пример № 2. Решить уравнение  1)   2)  3) Cравним правую часть уравнения  с  Здесь  Числа  не 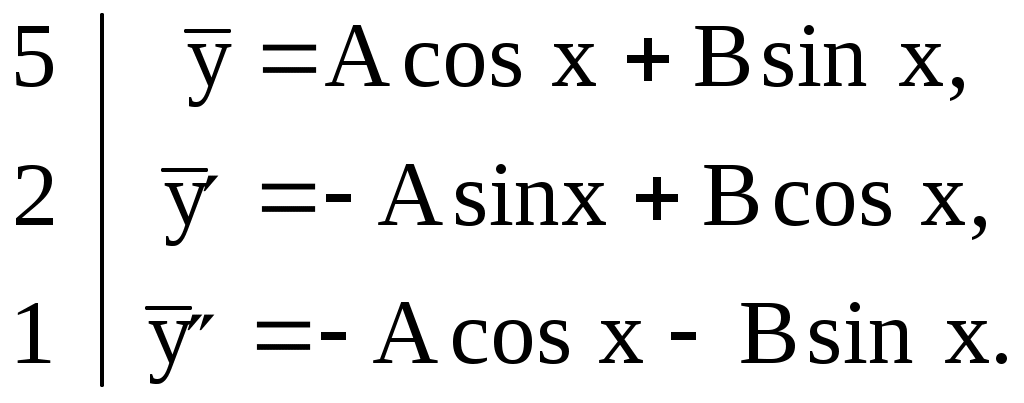являются корнями характеристического уравнения. Частное решение следует искать в виде 4) Запишем  Подставив  в уравнение, получим или    . Частное решение:  5) Общее решение данного дифференциального уравнения:  Пусть правая часть  неоднородного линейного д.у. II представляет собой сумму функций вида  или   Частное решение  этого уравнения следует искать в виде суммы  частных решений двух уравнений: и  № 3. Решить уравнение  Здесь   1)  2)  3) При 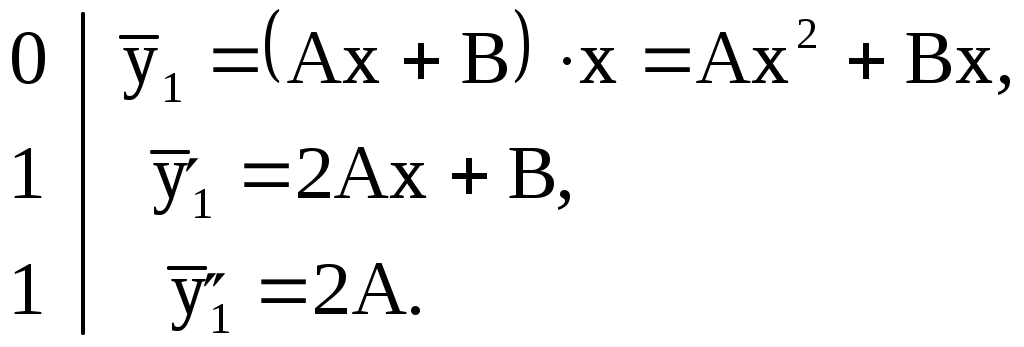  .    4) При 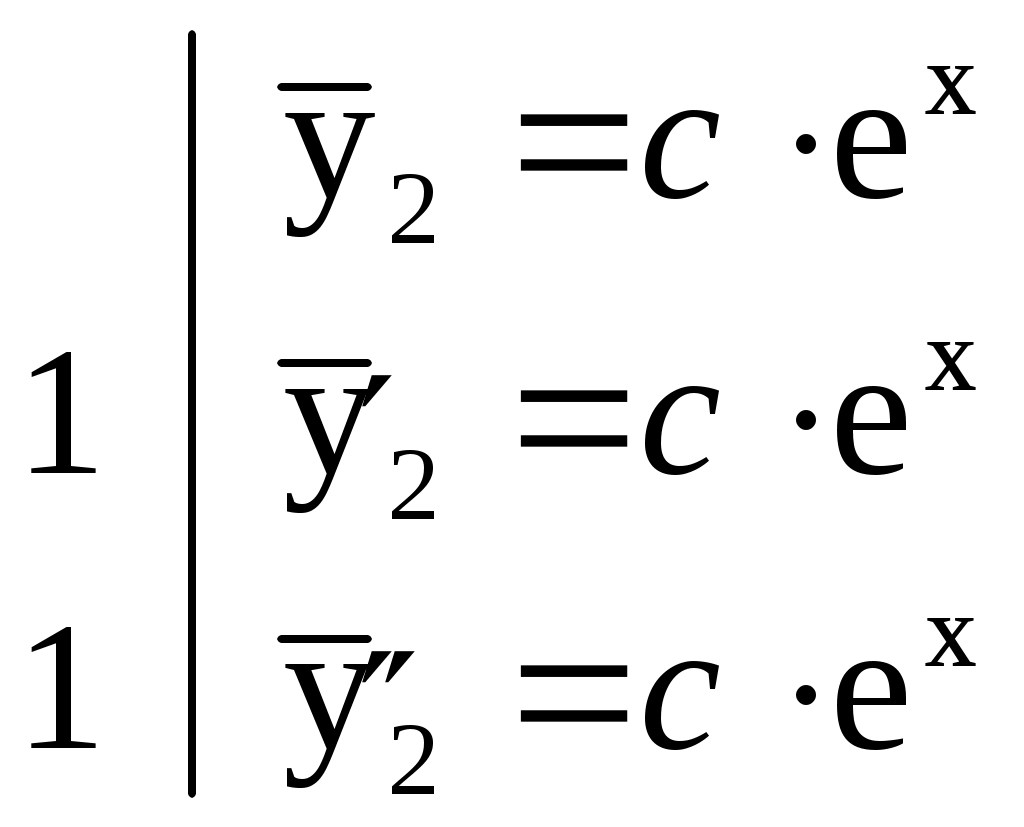     5) Общее решение данного дифференциального уравнения:  или  Метод вариации произвольных постоянных, метод Лагранжа. Рассмотрим метод вариации произвольных постоянных для уравнения второго порядка  (1)Если известна фундаментальная система решений соответствующего однородного уравнения  , (2),то общее решение неоднородного уравнения (1) может быть найдено методом вариации постоянных (метод Лагранжа). Общее решение уравнения (2) имеет вид  , (3)где  – фундаментальная система решений (ф.с.р.), – произвольные постоянные.Решение уравнения (1) будем находить в виде 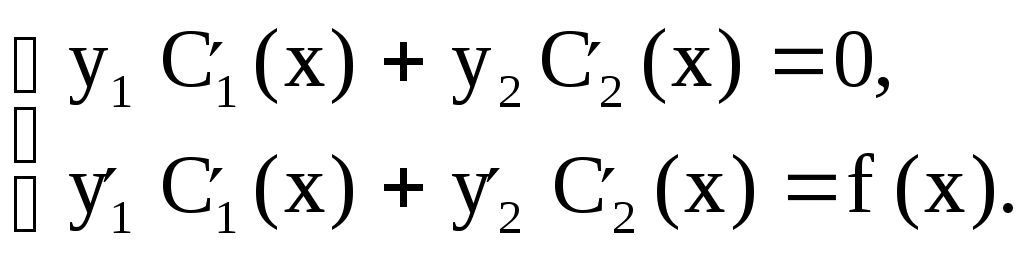 , (4)где  – некоторые пока неизвестные функции от х. Для их определения получаем систему (5)Решая (5) относительно  , получим (6) – определитель Вронского. , т. к. – ф. с. р.Из (6) находим  ,где  – постоянные интегрирования.Пример. Решить уравнение  .Решение. Соответствующее однородное уравнение будет  .Его характеристическое уравнение  и общее решение имеет вид  .Общее решение исходного уравнения имеем в виде  (*) – ф. с. р. – неизвестные функции от  . Для их нахождения составим систему 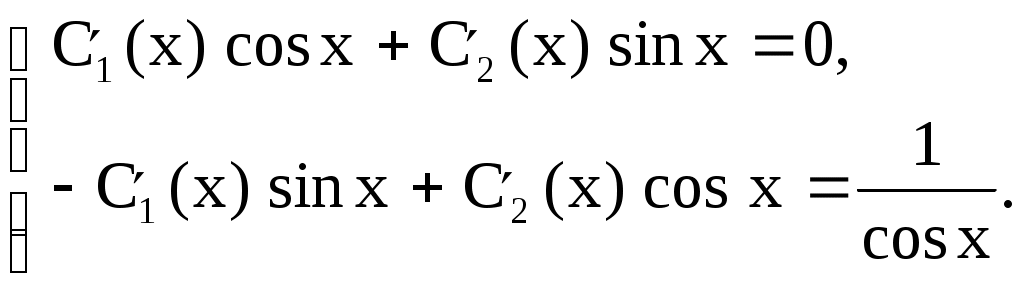 Решаем эту систему относительно  : .Интегрируя, находим  .Подставляя выражения  в (*), получаем общее решение искомого уравнения .Здесь  – частное решение исходного уравнения.Упражнения. Решить уравнения. 1)  . Ответ:  .2)  . Ответ:  .3)  . Ответ:  .4)  . Ответ:  ,или  . |