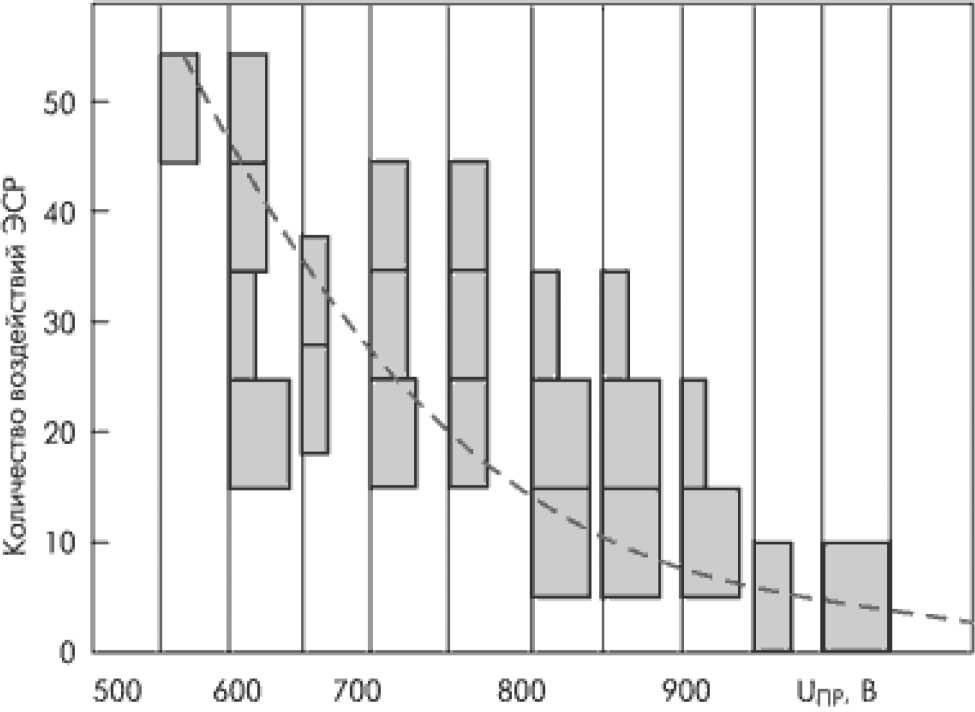
Моделирование ЭСР. 2 Разработка методов оценки надежности бортовой радиоэлектронной аппаратуры космических аппаратов

• Название: 2 Разработка методов оценки надежности бортовой радиоэлектронной аппаратуры космических аппаратов
• Дата: 05.04.2023
• Размер: 212.37 Kb.
• Имя файла: Моделирование ЭСР.docx
• Тип: Документы; #1038593
• страница: 3 из 6

На рис. 2.2, в качестве примера, приведены результаты эксперимента по установлению величин электростатических разрядов соответствующей полярности, влияющих на изменение вольтамперных характеристик и отказ биполярных больших интегральных схем (БИС) серии 1005.


Рис. 2.2. Зависимость отказов БИС серии 1005 от числа воздействий и величины



электростатического разряда

Развитие отказов в КМОП ИС, связанных с воздействием статического

электричества, не зависит от степени интеграции и определяется реальным уровнем стойкости конкретной микросхемы (за счет соответствующих схемотехнических и технологических решений) и условиями ее применения, зависящими только от изготовителя БРЭА.






При расчетах надежности БРЭА на КМОП ИС влияние ЭСР учитывается слагаемым Хеоз, которое входит в математическую модель интенсивности отказов, приведенную в стандарте М1Б-НОБК-217Б [34]. Х_еоз характеризует устойчивость микросхем к воздействию разряда статического электричества. Аргументом функции Х_еоз является стойкость к воздействию электростатического разряда (У_тн):

^КЕО8 '^еХР ( ^КЕО8 ' ^ТН )]

Г-4

^КЕО8

^ЕО8

ЕО8

(2.3)



К¹ К² К 3 К 4

где: ^ЕО8, ^ЕО8 , ^ЕО8, ^Е'^г - постоянные коэффициенты; У_ТН - стойкость к

воздействию электростатического разряда.

Так, например, КМОП СБИС, разрабатываемых и изготавливаемых в базовом технологическом процессе изготовления микросхем с минимальным топологическим размером 0,35 мкм, значение !_еО§ - не более 4,4-10^-9 ч^-1.

На рис. Х.3 приведен график зависимости Х_еО§-10^-6 от У_ТН, построенный по модели (2.3).

-8

8-10 ⁸

6-10 ⁸

. “8

Ь_ео<УЛ1)1 -10

2-10 ⁸

0 1 -104 2-104 3-104 4-104

УШ1

Рис. 2.3. Зависимость !_еО§ от У_ТН

Как видно из графика, при увеличении Утн интенсивность отказов снижается. Поэтому, при конструировании БРЭА на КМОП ИС следует применять микросхемы с высокой стойкостью к воздействию электростатического разряда [35].

Значения У_ТН могут быть получены на основе данных, приведенных в Иеуюе гейаЬййу герой фирм-производтелей. На рис. 2.4 приведен фрагмент Иеуюе гейаЬййу герой компании ХШСХХ.

ТаЫе 1-8: Ргодис! Е80 апд 1_а1сИ-ир 0а1а

Оехлсе	1_а1сЬ-ир	Нитап Войу Мос!е1	СНагде 0е71се Моде1
ХС17хххй/Ь	±200 шА	±2,000У	+2,000У(!)
ХС17хххЕ, ХС178ххх	+210 тА	±2,000У	±1,000У(2)
ХС17Уххх	+200 тА	±2,000У	±500У
ХС18Уххх	+200 тА	±2,000У	±500V®
ХС31ххх/А	+250 тА	±1,750У Ю ±8,000У	±1,000У<4)
ХСЗххх/А	+220 тА	±4,000У 1о±7,000У	±2,000У<5)
ХС4ххх/А	+300 тА	±1,000V 1о+8,000У	±2,000У<6)
ХС4хххЕ	+250 тА	±3,000У 1о±8,000У	±2,0007(7)
ХС4хххЕХ	+250 тА	±3,000У Ю ±7,000У	±2,000У<8>
ХС4хххХЬ	±250 тА	±2,000У Ю ±8,000У	±1,000У<9)
ХС4хххХЬА	±260 тА	±2,000У Ю ±7,000У	±500У (Соге)/±1,000У (согпег)(10)
ХСУххх	±200 тА	±1,000У Ю±2,000У	±500У(И)

16

уууууу.хШпх.сот
НеНаЬПИу Рерог!

1X3116 (у9.1) АидизХ 22, 2012

Рис. 2.4. Фрагмент Иеухее геНаЫШу герой компании ХГБГХХ

Т.к. Эеухее геНаЫШу герой обновлются раз в квартал, то для получения достоверной информации о величине У_тн необходимо проводить мониторинг данных о характеристиках надежности ЭРИ [10].

4. 
   Методы учета влияния теплового режима на надежность БРЭА КА
   

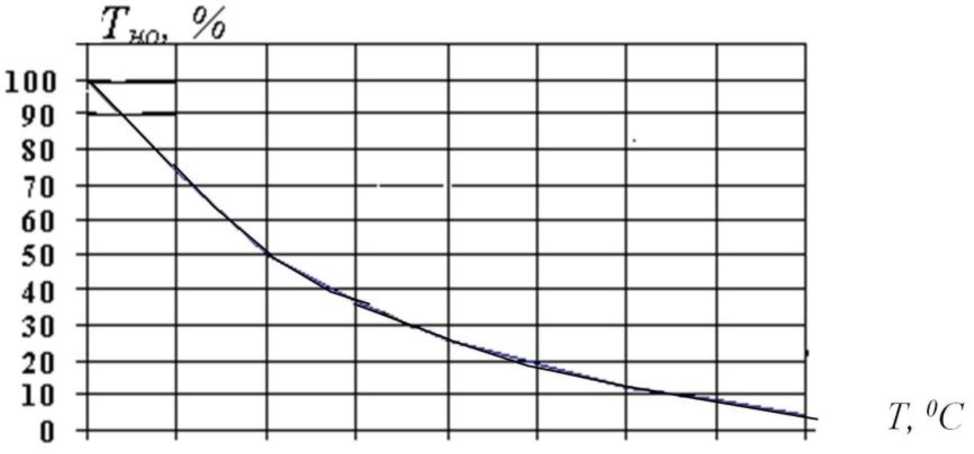
Тепловой режим БРЭА в значительной степени определяет показатели ее надежности. Так, например, увеличение температуры ЭРИ с 60 °С до 80 °С снижает среднее время наработки на отказ БРЭА почти в 2 раза (см. рис. 2.5).




40 50 60 70 80 90 100 110 120

Рис. 2.5. Типовая зависимость относительного изменения среднего времени наработки на отказ (Т_НО) от температуры

Однако, обеспечение тепловых режимов работы ЭРИ с точки зрения требований технических условий (ТУ) является необходимой, но далеко не достаточной гарантией обеспечения требований по надежности БРЭА. Это связано с тем, что в модели эксплуатационной интенсивности отказов ЭРИ входят коэффициенты, зависящие от рабочей температуры элемента.

Математические модели этих коэффициентов основаны на законе Аррениуса, который применяется для описания температурной составляющей деградационного процесса. С.А. Аррениус впервые ввел понятие «активационного комплекса» в статистическую теорию скоростей химических реакций в растворах.

Согласно этой теории процессу химического взаимодействия предшествуют более быстрые процессы «активации» и установления статистического равновесия. При этих условиях оказывается справедливым уравнение Аррениуса, описывающее зависимость константы скорости химической реакции (Кр) от абсолютной температуры:

Се.



(2.4)
Кр, (Т )= А ■ ехр 1^^^

где: К_р(Т) - константа скорости химической реакции; А - частота столкновений реагирующих молекул; Е_А - энергия активации; к- постоянная Больцмана; Т - температура.

Величина ехр[-Е_А/(к-Т)] характеризует вероятность того, что частицы имеют энергию, достаточную для вступления в реакцию, или долю активных столкновений при температуре Т; коэффициент А является частотным фактором, означающим общее количество столкновений; постоянная Е_А определяется для каждого процесса его особенностями.

При моделировании постепенных отказов в твердых телах, возникающих в результате деградационных процессов, положения теории скоростей химических реакций часто «переносятся» и на эти процессы. Широкий круг физико-химических процессов, помимо чисто химических реакций, связан с изменением концентрации вещества в результате переноса частиц и их взаимодействия (например, диффузия в объеме и на поверхности кристалла и корпуса ИС, перемещение элементарных точечных и линейных дефектов и др.), удовлетворяет основным законам этой теории. Аналогия деградационных процессов в твердых телах химическим реакциям подсказывает простой способ моделирования температурной зависимости времени до отказа !(Тд) в виде экспоненциальной функции:

I (Т, ) = — = = — ■ ехр

К Е ^ А ¹



(2.5)
^р А ■ ехр' — ¹

где: 1о - время до отказа; К_р - константа скорости химической реакции; Е_А - энергия активации; к- постоянная Больцмана; Тд - температура кристалла (кристаллической решетки).

Эта аналогия не формальна и находит практическое подтверждение при анализе реальных деградационных процессах в твердых телах. Однако на практике вместо К_р(Т|) используют отношение К_р(Т;)/К_р(Т₀) = К_Т, которое показывает, во сколько раз время до отказа при температуре Т меньше, чем при температуре То. При этом за То принимают температуру кристалла, соответствующую «нормальным условиям, равную 298 °К. Тогда:

/ X А тг кр(т) а ■ е кЕ ( Е. Е ^ Г Е ( 1 1 ^ КТ= == ехр+ = ехр■ 1К (Т ) Е-к-Т к-Т к Т Т Кр(Т0) А кТ к к Т к Тт 7 к кТ Т°7

], (2.6)