земельный кадастр билеты госы. 2. Современная философия науки, её предмет и особенности
 Скачать 0.81 Mb.
|
Автоматизация тахеометрической съемкиС появлением электронных тахеометров стало возможным автоматизировать процесс измерений и вычислений при выполнении тахеометрической съемки. Для этого электронный тахеометр устанавливают на станции тахеометрического хода, а на реечные точки (пикеты) устанавливают последовательно вешку со светоотражателем вместо рейки. При наведении электронным тахеометром на отражатель в автоматическом режиме определяются горизонтальные и вертикальные углы, расстояния на заднюю и переднюю точки хода и пикеты. С помощью микроЭВМ тахеометра выполняется обработка результатов измерений, в результате которой получают приращения координат и превышения на смежные точки тахеометрического хода и снятые реечные точки. Результаты измерений могут быть введены в специальное запоминающее устройство тахеометра (накопитель информации) или переписаны на флэш-карту. В дальнейшем из запоминающего устройства или флэш-карты информация поступает в ЭВМ, которая по специальной программе производит уравнивание тахеометрического хода и вычисление координат и высот станций и пикетов. По полученным данным с помощью графопостроителя, соединенного с ЭВМ, осуществляется графическое построение топографического плана тахеометрической съемки. Другим способом совершенствования и автоматизации тахеометрической съемки является применение методики, при которой отпадает необходимость во взаимной видимости между смежными точками тахеометрического хода, что приводит к уменьшению числа станций на снимаемой территории. В этом случае для связи двух соседних станций тахеометрического хода используются общие с в я з у ю щ и е т о ч к и, которые необходимо снять с обеих станций электронным тахеометром. Определив координаты и высоты этих связующих точек с первой стоянки тахеометра можно через них определить координаты и высоты точек второй стоянки тахеометра в единой для двух стоянок системе координат и высот. Таким образом, опорная съемочная сеть может быть создана без специального проложения теодолитно-тахеометрического хода в процессе выполнения тахеометрической съемки. Мощным средством автоматизации тахеометрической съемки является применение современных программных комплексов для обработки результатов измерений. Такие комплексы позволяют решать все необходимые задачи для получения топографического плана съемки в электронном виде, что сделает возможным создание безбумажной технологии в геодезии. Наиболее распространенным программным комплексом для изысканий и проектирования инженерных сооружений является «CREDODIALOGUE» в результате применения, которого можно получить цифровую модель местности. Подробно системы этого комплекса были рассмотрены в разделе «Теодолитная съемка». Опишите алгоритм создания слоя для хранения объектов «здания» в ГИС MapInfo БИЛЕТ №12 Классификация ошибок геодезических измерений. Свойства случайных ошибок измерений. Понятие о предельной ошибке. Классификация ошибок измерений. Основные постулаты теории ошибок. Кривая Гаусса и её свойства. Свойства случайных ошибок. КРИТЕРИИ ТОЧНОСТИ ИЗМЕРЕНИЙ. Средняя квадратическая ошибка и её достоинства. Вероятная и средняя ошибки и их связь со средней квадратической ошибкой при нормальном законе распределения. Исследование на нормальный закон распределения ряда истинных ошибок. ОШИБКИ ОКРУГЛЕНИЙ И ИХ СВОЙСТВА. Понятие о равномерном законе распределения ошибок округления. Средняя квадратическая ошибка округлений, её связь с предельной ошибкой округления. СРЕДНЯЯ КВАДРАТИЧЕСКА ОШИБКА ФУНКЦИЙ (коррелированных и некоррелированных аргументов). Типовые примеры. РАВНОТОЧНЫЕ ИЗМЕРЕНИЯ. Основные этапы математической обработки ряда многократных независимых равноточных измерений одной величины. Определение наиболее надёжного значения измеряемой величины. Определение средней квадратической ошибки отдельного результата измерений. Определение средней квадратической ошибки наиболее надёжного значения. Построение доверительных интервалов, с заданной вероятностью накрывающих неизвестные точные значения параметров: истинного значения и среднего квадратического отклонения отдельного результата измерений. Порядок обработки ряда равноточных измерений одной величины, выполняемый по определённой схеме со всеми необходимыми контролями вычислений. НЕРАВНОТОЧНЫЕ ИЗМЕРЕНИЯ. Понятие о весе. Обратный вес функции коррелированных и некоррелированных аргументов. Основные этапы математической обработки ряда многократных независимых неравноточных измерений одной величины. Определение среднего весового: наиболее надёжного значения измеряемой величины. Определение средней квадратической ошибки измерения с весом, равным единице. Определение средней квадратической ошибки наиболее надёжного значения. Построение доверительных интервалов для истинного значения и среднего квадратического отклонения измерения с весом, равным единице. Порядок обработки, необходимые контроли вычислений. ДВОЙНЫЕ ИЗМЕРЕНИЯ. Математическая обработка двойных равноточных измерений ряда однородных величин. Критерий обнаружения систематических ошибок. Математическая обработка двойных неравноточных измерений ряда однородных величин. Порядок обработки, необходимый контроль вычислений. Ошибки измерений подразделяют на грубые, систематические и случайные. К грубым ошибкам относят ошибки, вызванные промахами и просчётами наблюдателя, неисправностями приборов, резким ухудшением внешних условий и др. С целью их обнаружения измерения выполняются многократно (не менее двух раз). Результаты измерений, содержащие грубые ошибки, необходимо выявлять и исключать из обработки. К систематическимотносят ошибки, которые входят в результаты измерений по тому или иному закону, как функции источников возникновения ошибок. В практике геодезических измерений применяют следующие способы уменьшения влияния систематических ошибок: 1. Устанавливают закон появления систематических ошибок, после чего ошибки уменьшают введением поправок в результаты измерений; 2. Применяют соответствующую методику измерений для того, чтобы систематические ошибки действовали не односторонне, а изменяли знаки; 3. Используют определённую методику обработки результатов измерений. Случайные ошибки являются наиболее ярким примером случайной величины. Их закономерности обнаруживаются только в массовом проявлении. Случайные ошибки неизбежны при измерениях и не могут быть исключены из единичного измерения. Влияние их можно лишь ослабить, повышая качество и количество измерений, а также надлежащей математической обработкой результатов измерений. Причин возникновения случайных ошибок измерений много: влияние внешних условий, неточности изготовления и юстировки приборов, неточности выполнения операций наблюдателем и т. д. Очевидно, что случайные ошибки являются результатом суммирования большого числа независимых элементарных ошибок. На основании центральной предельной теоремы Ляпунова можно считать, что случайные ошибки измерений подчиняются нормальному закону распределения. В дальнейшем условно примем, что в любых измерениях грубые ошибки отсутствуют, основная часть систематических ошибок исключена из результатов, а остаточные систематические ошибки ничтожно малы, т. е. будем рассматривать только случайные ошибки (  , где хi — результат измерений, Х — истинное значение измеряемой величины.) Очевидно, что  , а  .3 СВОЙСТВА СЛУЧАЙНЫХ ОШИБОК ИЗМЕРЕНИЙ 1. Случайные ошибки по абсолютной величине с заданной вероятностью b не должны превышать определённого предела, равного  (t — коэффициент, для которого  , m — средняя квадратическая ошибка)*);2. Положительные и отрицательные случайные ошибки, равные по абсолютной величине, одинаково часто встречаются в ряде измерений; 3. Среднее арифметическое из значений случайных ошибок при неограниченном увеличении числа измерений имеет пределом нуль, т. е.
Это свойство называют свойством компенсации. Отклонение  от нуля свидетельствует о наличии в результатах измерений систематических ошибок.4. Малые по абсолютной величине случайные ошибки встречаются в ряде измерений чаще, чем большие. 1.4 КРИТЕРИИ ТОЧНОСТИ ИЗМЕРЕНИЙ Основным критерием точности результатов измерений является средняя квадратическая ошибка (оценка СКО), определяемая по формуле
Для ряда истинных ошибок  при известном  формула принимает вид (1.3) и называется формулой Гаусса:
где  ;  .Средней ошибкой называют среднее арифметическое из абсолютных значений ошибок, т. е.
Вероятной ошибкой  называют такое значение случайной ошибки D, больше или меньше которого, по абсолютной величине, ошибки равновозможны, т. е. .На практике определяется величиной, которую находят, расположив все ошибки Di в ряд в порядке возрастания их абсолютных величин. Вероятная ошибка будет расположена в середине такого ряда.При нормальном законе распределения случайных ошибок имеют место соотношения:
Величины и являются оценками параметров J и r: соответственно среднего и вероятного отклонений (см. раздел I п. 3.5).Соотношения называют критериями нормального закона (в разделе I они представлены в виде  ;  ).Предельной ошибкой  называют такую ошибку, больше которой в ряде измерений ошибок не должно быть. В качестве предельных выбирают величины, определяемые по правилу и  (с вероятностями 0,954 и 0,997 соответственно). Перечисленные выше критерии  , m, , ,  называют абсолютными ошибками.Относительной ошибкой называют отношение соответствующей абсолютной ошибки к значению измеряемой величины X (если X неизвестно, его заменяют результатом измерения x). Относительную ошибку обычно выражают в виде дроби с числителем, равным 1, например:  — средняя квадратическая относительная ошибка; — предельная относительная ошибка величины Xи т. д. Значения абсолютных ошибок получают с двумя–тремя значащими цифрами, а знаменатель относительной ошибки округляют до двух значащих цифр с нулями. Например, при  и  . .Предельная ошибка. Вследствие третьего свойства случайные ошибки, превышающие по абсолютной величине значение 2m, встречаются редко (5 на 100 измерений). Еще реже погрешности больше 3m (3 из 1000 измерений). Поэтому устроенную погрешность называют предельной ошибкой Для особо точных измерений в качестве предельной ошибки принимают Все вышеперечисленные ошибки называют абсолютными. В геодезии в качестве специальных характеристик точности измерений используется относительная ошибка – отношение абсолютной ошибки к среднему значению измеряемой величины, которое выражается в виде простой дроби с единицей в числителе, например Предельная ошибка ∆пред вычисляется по формуле ∆пред =tβ ⋅ m, (15) где β t – аргумент интеграла вероятностей t( ) Φ β в предположении о нормальном законе распределения результатов измерений. Для доверительной вероятности β = Φ(tβ ) = ,0 954 tβ = ;0,2 β =Φ(tβ ) = ,0 988 t = 2,5; β β = Φ(tβ ) = ,0 997 tβ = .0,3 Ошибки, превышающие по абсолютной величине предельную, считаются недопустимыми. Такие измерения бракуют. Методы определения эффективности мероприятий по совершенствованию организации труда. Организация труда имеет экономическую, психофизиологическую и социальную направленность, которая, соответственно, выражается в экономическом, психофизиологическом и социальном эффекте, что отражается в совокупном экономическом эффекте. Расчет экономической эффективности проводится путем сопоставления трудовых, материальных и финансовых затрат до и после реализации мероприятий по организации труда или сравнением фактических затрат с нормативными. Экономическая эффективность организации труда выражается группами стоимостных и трудовых показателей. Показателями экономической эффективности мероприятий по совершенствованию организации труда являются: изменения (повышение или снижение) производительности труда; относительное сокращение или увеличение численности работающих, уменьшение или увеличение трудоемкости сравнимого объема работ или продукции; повышение или снижение качества продукции; изменения удельного веса брака продукции или работ; изменения удельных расходов материальных затрат в расчете на единицу продукции или на тысячу (миллион) рублей прибыли. Обобщающим показателем экономической эффективности как отдельного мероприятия, так и их совокупности является снижение затрат на производство и увеличение прибыли. Экономическая эффективность Ээф выражается в стоимостных (денежных) показателях и рассчитывается в общем виде как разность между полученной (или ожидаемой) экономией Эк и затратами З: Ээф = Эк – З. Но это приблизительная схема эффективности. На практике в показатель экономии Эк включается не только сумма снижения себестоимости, но и увеличение прибыли, получаемой или ожидаемой от увеличения объемов производства, изменений в ассортименте продукции или ожидаемого изменения оптовых цен на рынке. Показатель затрат также неоднороден. Методику расчета ожидаемой экономической эффективности мероприятий по совершенствованию организации труда можно свести к трем вариантам. Для случаев, когда продукция однородна или ее ассортимент невелик и возможно достаточно точно рассчитать себестоимость единицы продукции до и после осуществления конкретного мероприятия, расчеты могут производиться по формуле: Ээф = (С0 – С1) – ОП ± ΔОП × Ппр – Зед × Ен, где С0 – С1 – себестоимость единицы продукции до и после осуществления мероприятий, р. или тыс. р.; ОП – объем производства данного вида продукции в натуральном измерении; ΔОП – прирост (+) или уменьшение (–) объема производства в натуральном измерении; Ппр – размер прибыли на одну натуральную единицу продукции, р. или тыс. р.; Зед – сумма единовременных (капитальных затрат), р. или тыс. р.; Ен – коэффициент сравнительной экономической эффективности единовременных (капитальных) затрат. 2. Для случаев, когда продукция неоднородна, выпускается в большом и постоянно меняющемся ассортименте, а изменение себестоимости каждого вида продукции на стадии проектирования мероприятий рассчитать с достаточной точностью затруднительно, расчет ожидаемой экономической эффективности ряда мероприятий может выполняться по формуле: Ээф = Эчисл × ЗПср × Котч – Зтек – Зед × Ен, где Эчисл – относительное сокращение численности работников за счет улучшения организации труда, чел.; ЗПср – средняя заработная плата одного высвобожденного работника за расчетный период (год), тыс. р.; Котч – коэффициент отчислений от заработной платы в страховой, пенсионный и другие фонды. 3. Для случаев, когда экономический эффект при разнородной и часто меняющейся продукции рассчитывается исходя из прироста объемов производства и экономии на условно-постоянных расходах без изменения численности промышленно-производственного персонала, ожидаемая экономическая эффективность всего комплекса мероприятий определяется по формуле: Ээф = ΔОП × Сб × dупр + ΔОП × (Ппр/100) – Зтек – Зед × Ен, где ΔОП – прирост объемов производства, тыс. р. или натуральные показатели; Сб – базовая (плановая) себестоимость единицы продукции; dупр – удельный вес условно-постоянных расходов в себестоимости; Ппр – процент плановой прибыли на рубль продукции. Если вследствие проведения организационных мероприятий складываются различные темпы роста производительности труда и средней заработной платы, то в расчеты экономической эффективности вносятся коррективы на изменения себестоимости, как это изложено при рассмотрении первого случая определения экономического эффекта. Если расчеты показывают отсутствие экономической эффективности отдельных мероприятий или даже отрицательную эффективность (превышение затрат по сравнению с экономией от внедрения мероприятий), то план мероприятий пересматривается с внесением необходимых исправлений. Прокомментируйте, какие модули содержит PHOTOMOD StereoDraw PHOTOMOD StereoDraw - модуль для создания и редактирования 3D векторных объектов в стереорежиме. Содержит такие удобные инструменты, как автоматическое перемещение курсора по рельефу, 2D и 3D-снаппинг, векторизация сегментов линий под прямым углом, копирование векторных 12 объектов, автоматическое проведение линии вдоль границы существующего объекта, построение буферных зон и многие другие. К графическим объектам могут быть привязаны записи из классификатора и атрибуты. Поддерживается обширный набор векторных форматов импорта/экспорта. Кроме того, модуль содержит программу 3D-Mod для трехмерного моделирования и экспорта в формат DXF. БИЛЕТ №13 Растровая и векторная модели представления данных. Регистрация растрового изображения в MapInfo. Перенос координат с векторной карты на растровое изображение. Векторизаторы. Система автоматизированного проектирования (САПР). |
.
.
,
.
; 
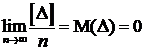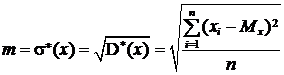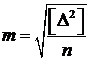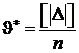