|
|
Статика7. 2. статика в статике изучаются условия равновесия твердых тел под действием сил
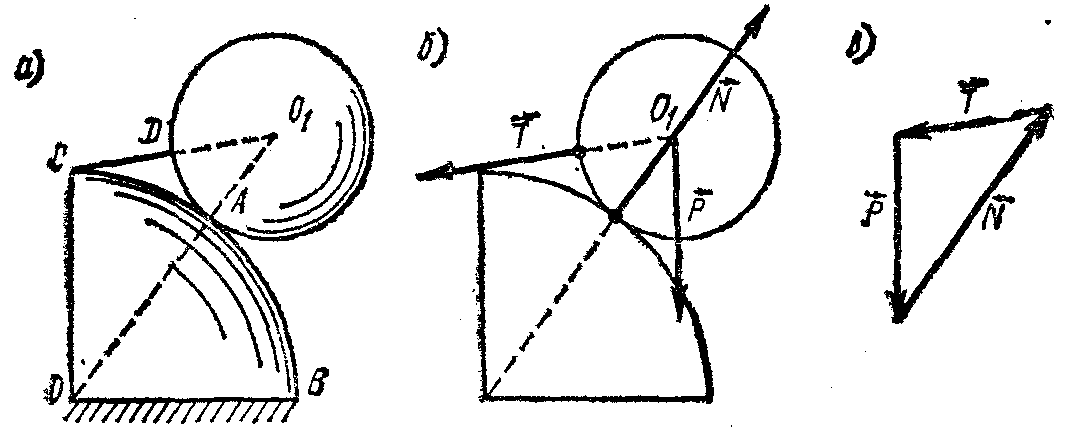 Рис. 179
Реакция  (рис. 179, б) цилиндрической поверхности направлена по общей нормали к цилиндрам и, следовательно, проходит через точку O1. Реакция (рис. 179, б) цилиндрической поверхности направлена по общей нормали к цилиндрам и, следовательно, проходит через точку O1. Реакция 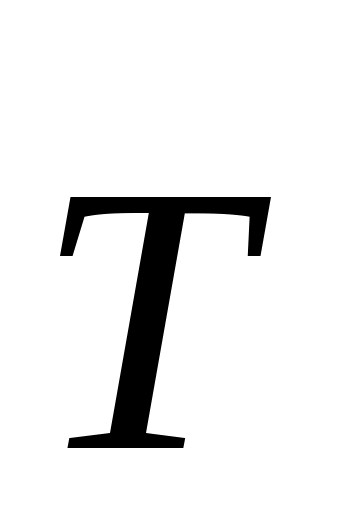 направлена по нити CD. Так как на цилиндр А действуют три силы, то на основании теоремы о трех силах их линии действия должны пересекаться в точке O1. Следовательно, цилиндр А при равновесии займет такое положение, при котором нить CD будет продолжением его радиуса. направлена по нити CD. Так как на цилиндр А действуют три силы, то на основании теоремы о трех силах их линии действия должны пересекаться в точке O1. Следовательно, цилиндр А при равновесии займет такое положение, при котором нить CD будет продолжением его радиуса.
Построим силовой треугольник (рис. 179, в). Этот треугольник подобен ΔОО1С. Из подобия треугольников
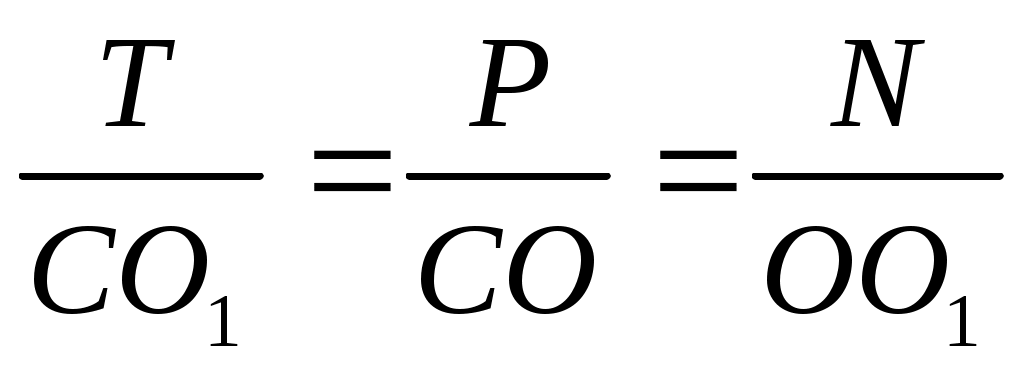
или
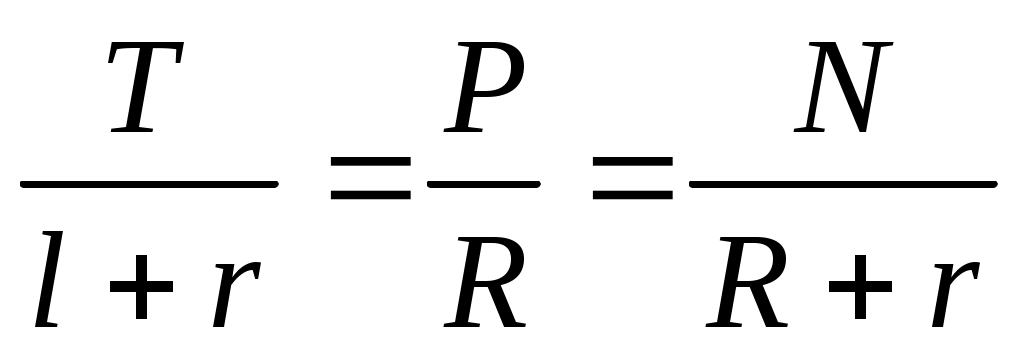 . .
Отсюда находим
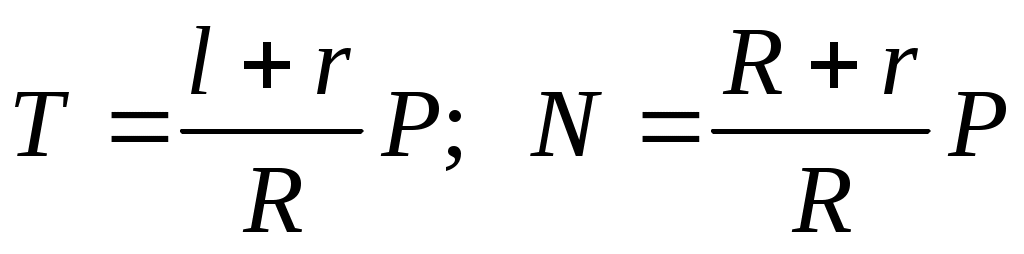 . .
Задачи Сложение и разложение сходящихся сил
2.1.1. Какую по модулю силу 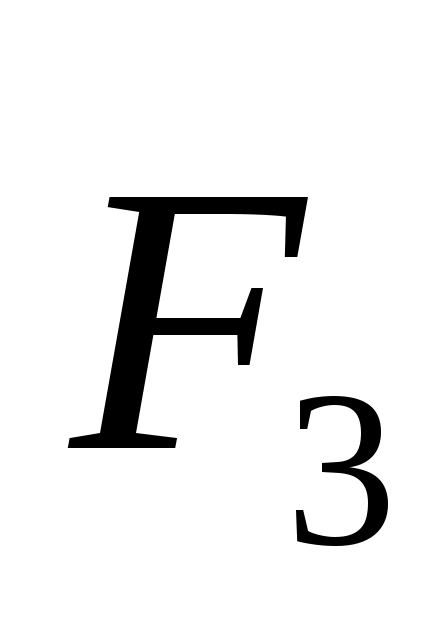 (рис. 180) надо приложить к сходящимся силам F1 = 2 Н и F2 = 4 Н, образующим с осью Ох углы α = 30° и β = 60°, чтобы равнодействующая этих трех сил равнялась нулю? (6,62) (рис. 180) надо приложить к сходящимся силам F1 = 2 Н и F2 = 4 Н, образующим с осью Ох углы α = 30° и β = 60°, чтобы равнодействующая этих трех сил равнялась нулю? (6,62)
2.1.2. Равнодействующая R= 10 Н двух сходящихся сил (рис.181)образует угол γ = 30°. Сила F1=5 Н образует с этой же осью Ох угол α = 60°. Определить модуль силы F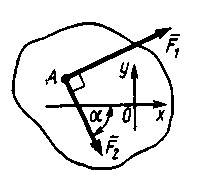 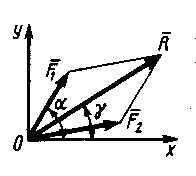 2. (4,64) 2. (4,64)
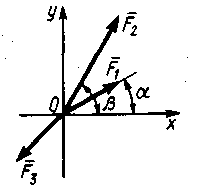
Рис.180 Рис.181 Рис. 182
2.1.3.На твердое тело (рис.182) в точке А действуют силы F1 = 6 Н и F2 = 3 Н, линии действия которых находятся в плоскости Оху. Определить сумму проекций этих сил на ось Ох, если уголα = 60°.(0,402)
2.1.4. На пресс (рис. 183) в точке О действуют силы F1= 5 Н и F2= 7 Н, линии действия которых находятся в плоскости чертежа. Определить модуль вертикальной силы, сжимающей материал, если заданы углы α = 30°,
β = 45°. (9,28)
2.1.5. К столбу (рис. 184) в точке А приложена плоская система сходящихся сил F1= F2 = F3 = 10 Н. Определить суммупроекций заданных сил на ось Ох, если угол α= 60°.(27,3)
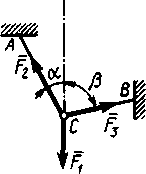
2.1.6. На твердое тело в точке О (рис. 185)действует плоская система сил F1 = 1 Н, F2 = 2 Н, F3 = 3 Н, F4 = 4 Н. Определить сумму проекций заданных сил на ось Оу, если з аданы углыα= 30°, β = 45°, γ= 60°. ( аданы углыα= 30°, β = 45°, γ= 60°. ( -3,22) -3,22)
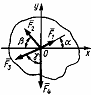
Рис.183 Рис. 184 Рис. 185
2.1.7.Для плоской системы сходящихся сил (Н):
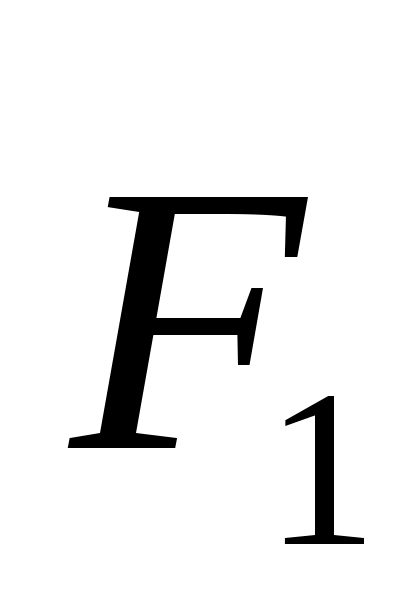 = 3 = 3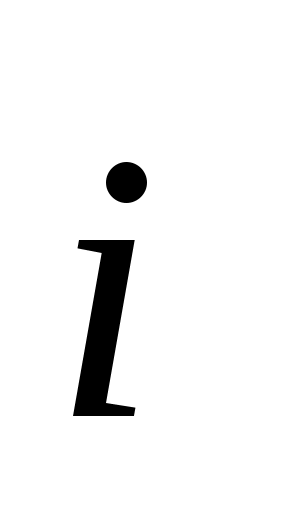 + 4 + 4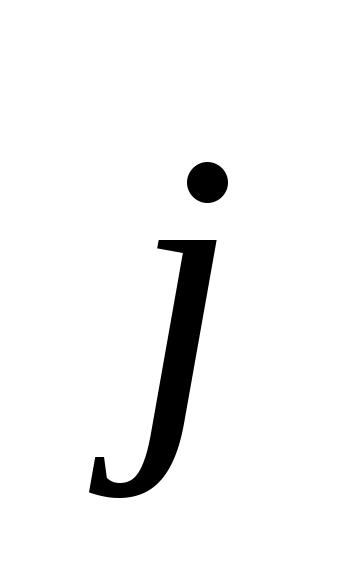 ; ; 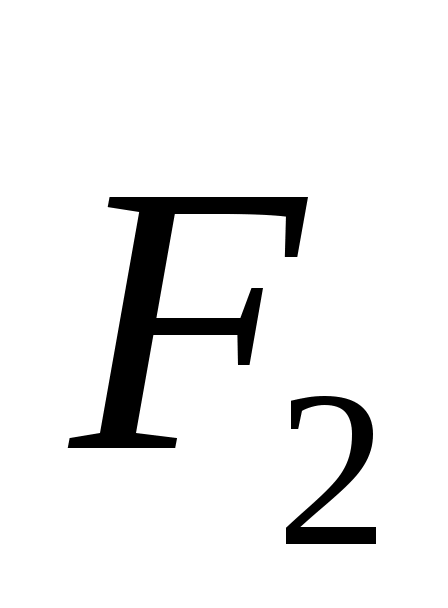 = 5 = 5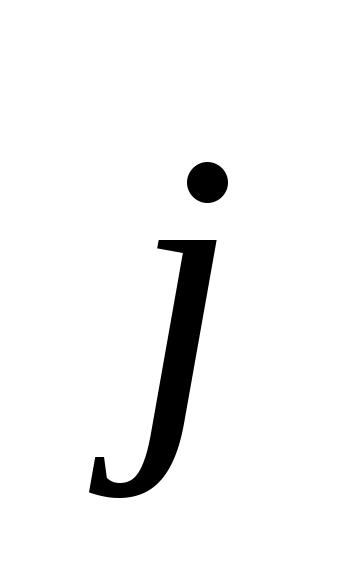 , , 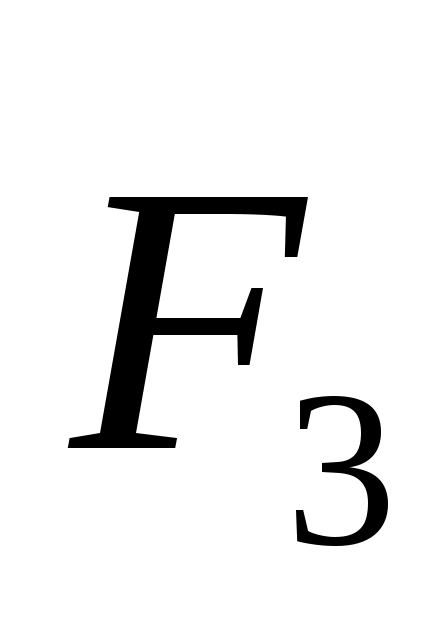 = 3 = 3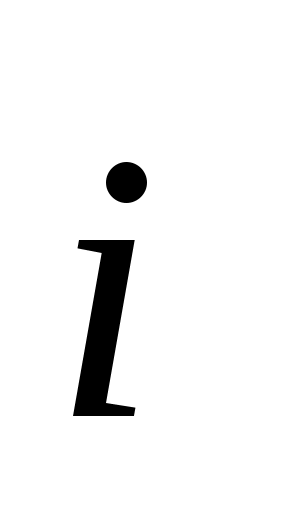 и определить модуль равнодействующей силы. (7,35) и определить модуль равнодействующей силы. (7,35)
2.1.8. Равнодействующая сходящихся сил 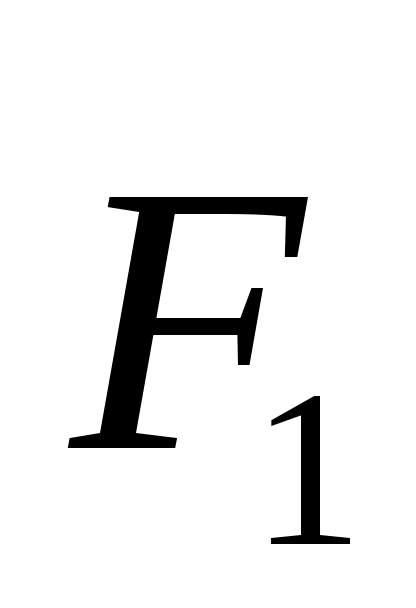 и и 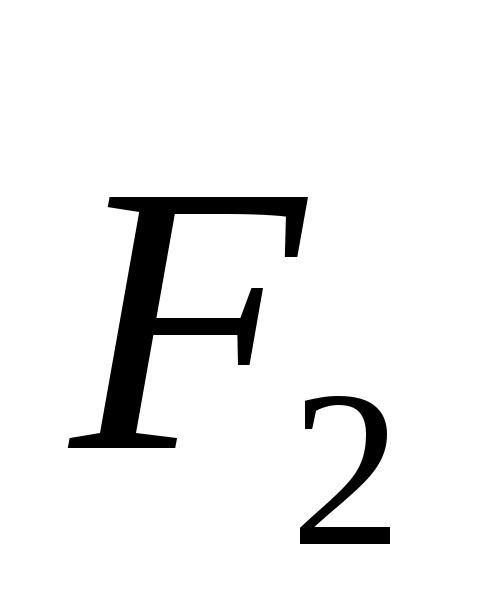 равна по модулюR = 8Н и образует с горизонтальной осью Ох угол α = 30°.Вектор силы равна по модулюR = 8Н и образует с горизонтальной осью Ох угол α = 30°.Вектор силы 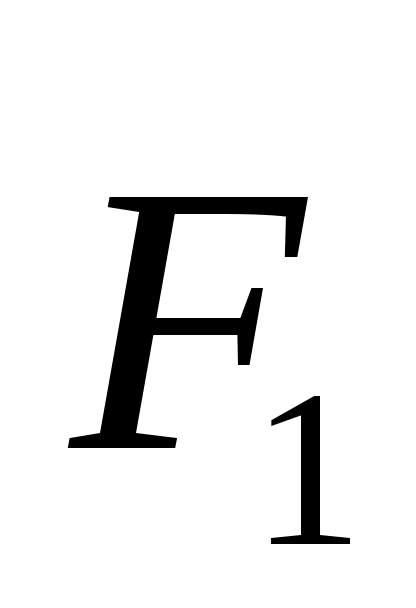 направлен по оси Ох,а вектор силы направлен по оси Ох,а вектор силы 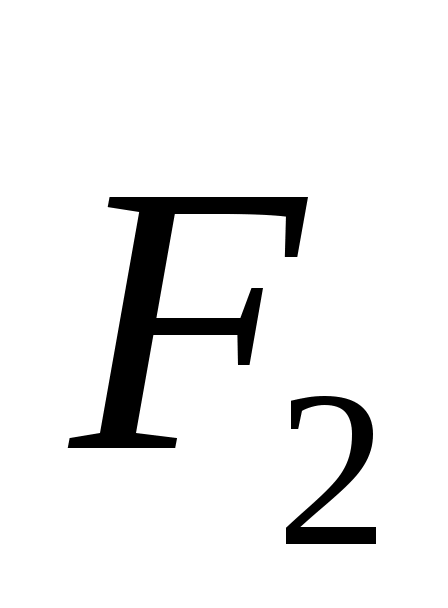 образует с этой осью угол β = 60°. Определить модуль силы образует с этой осью угол β = 60°. Определить модуль силы 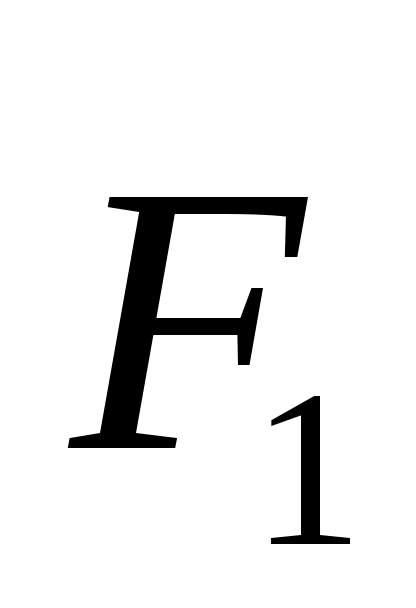 . (4,62) . (4,62)
2.1.9. Плоская система трех сходящихся сил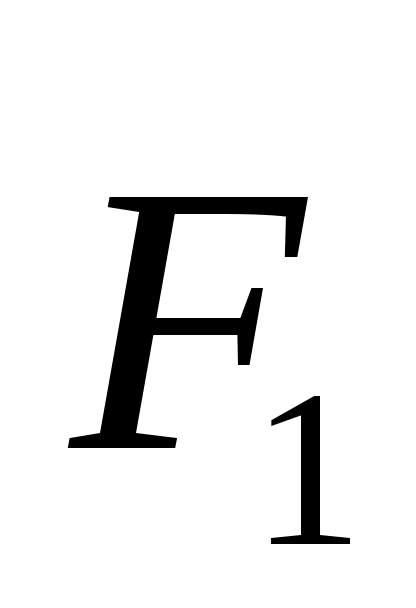 , , 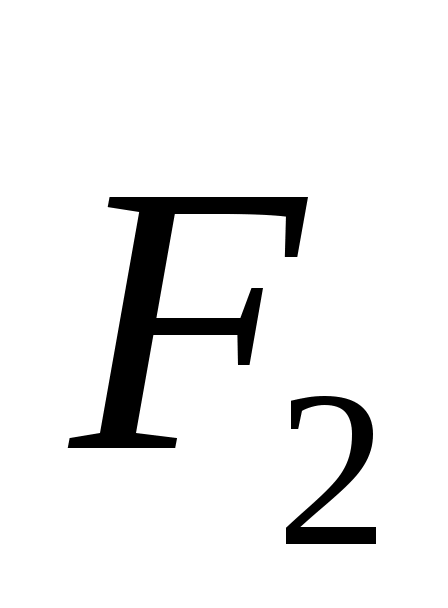 и и 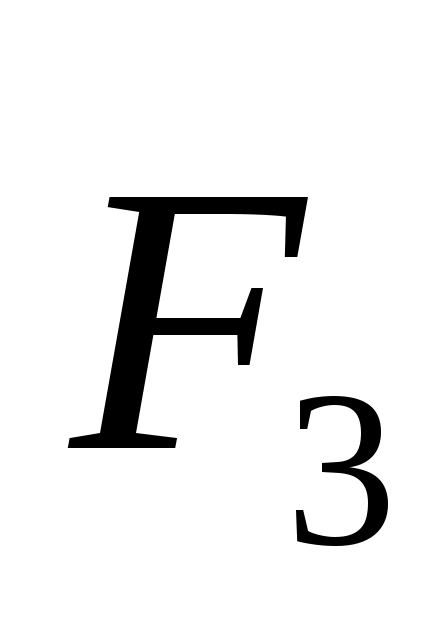 находится в равновесии. Заданы модули сил F1= 3 Н и F2 = 2 Н, а также углы, образованные векторами сил находится в равновесии. Заданы модули сил F1= 3 Н и F2 = 2 Н, а также углы, образованные векторами сил 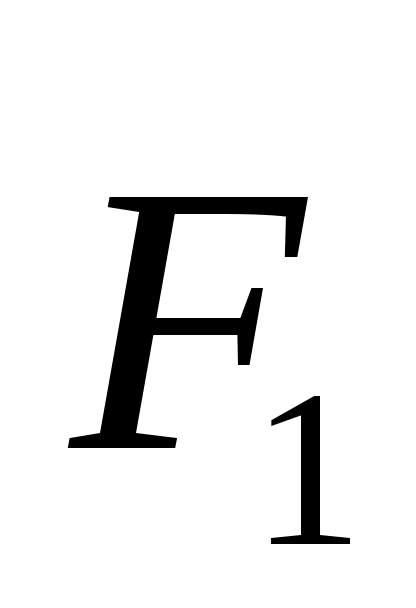 и и 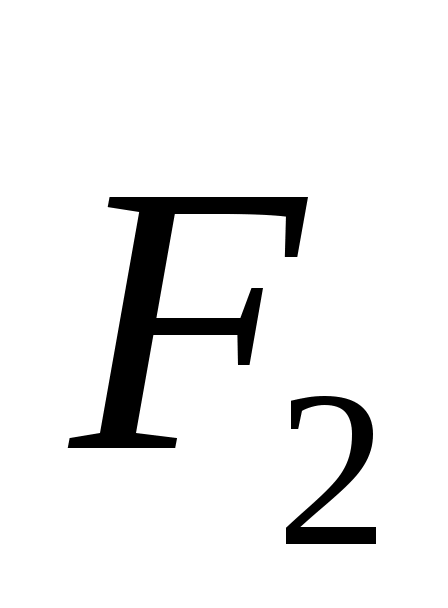 с положительным направлением горизонтальной оси Ох,соответственно равные α1= 15° и α2= 45°. Определить модуль силы с положительным направлением горизонтальной оси Ох,соответственно равные α1= 15° и α2= 45°. Определить модуль силы 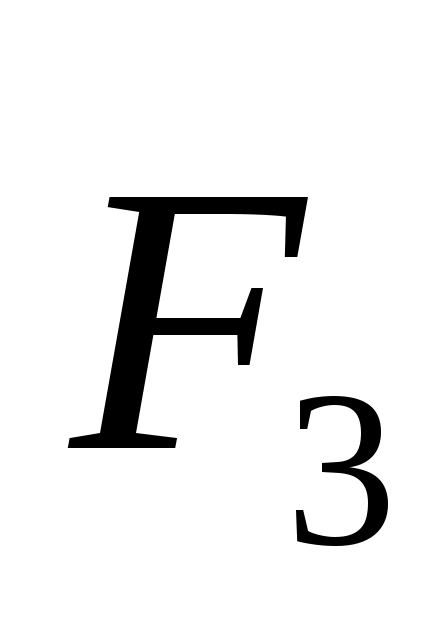 . (4,84) . (4,84)
2.1.10. Задана проекция Rx= 5 Н равнодействующей двух сходящихся сил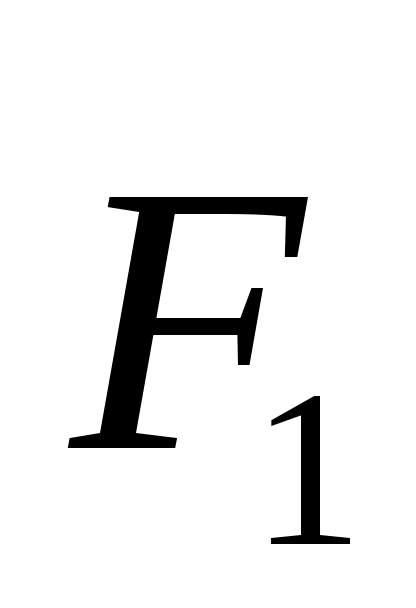 и и 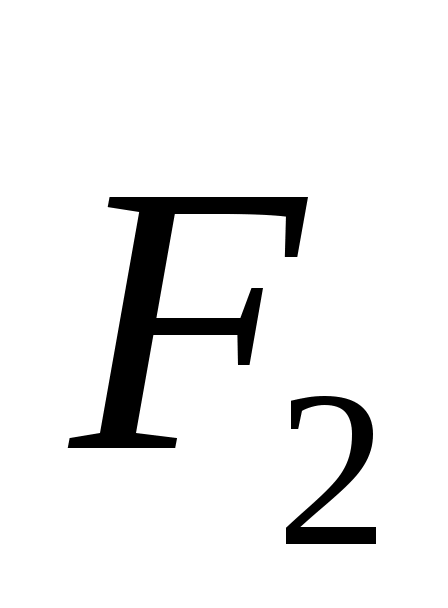 на горизонтальную ось Ох. Проекция силы на горизонтальную ось Ох. Проекция силы 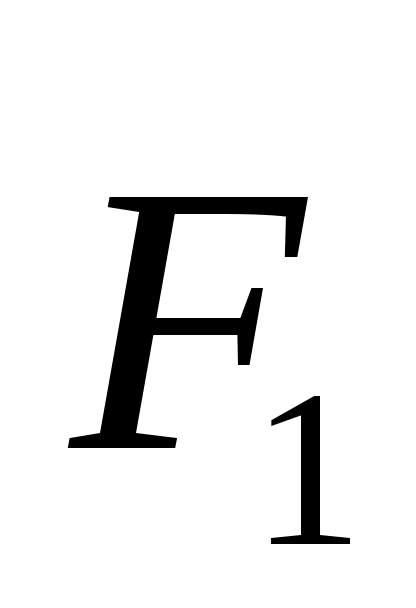 на эту же осьF1х = 7 Н. Определить алгебраическое значение проекции на ось ОхсилыF2.(-2) на эту же осьF1х = 7 Н. Определить алгебраическое значение проекции на ось ОхсилыF2.(-2)
2.1.11. Определить модуль равнодействующей сходящихся сил 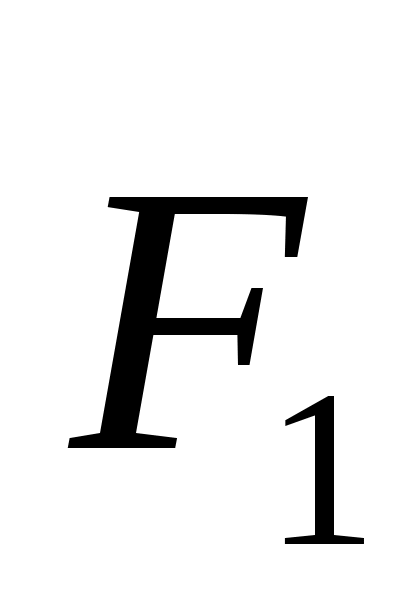 и и 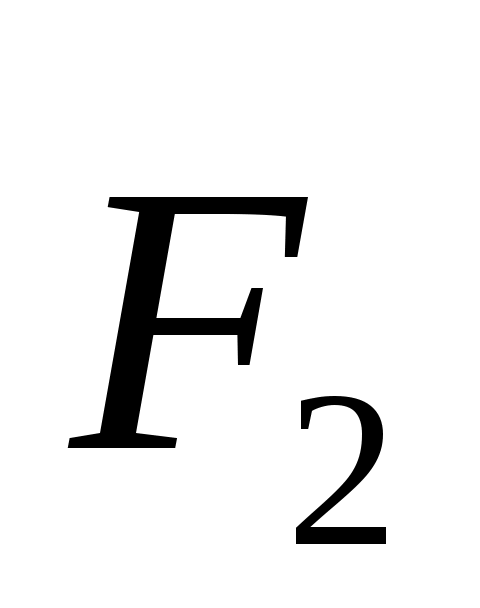 , если известны их проекции на декартовы оси координат: F1х= 3 Н, F1y= 6 Н, F2х= 5 Н, , если известны их проекции на декартовы оси координат: F1х= 3 Н, F1y= 6 Н, F2х= 5 Н,
F2y = 4 Н. (12,8)
2.1.12. Определить, находится ли данная плоская система трех сходящихся сил в равновесии, если извест-ны проекции сил на оси координат: F1х= 10 Н; F1y = 2 Н; F2x= - 4 Н; F2y = 3 Н; F3x = - 6 Н; F3у =- 5 Н. (Да)
2.1.13. Равнодействующая плоской системы сходящихся сил 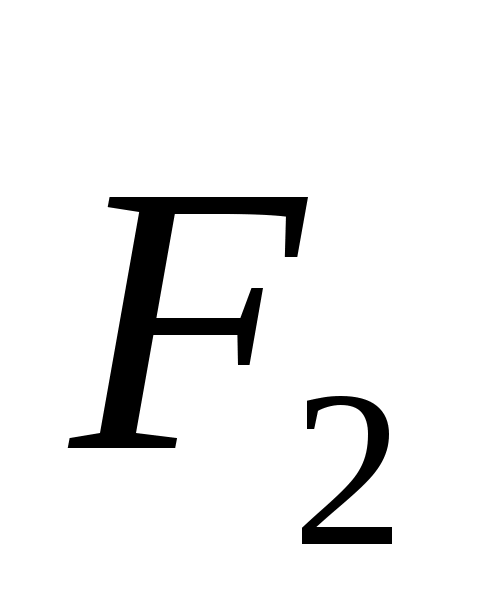 , ,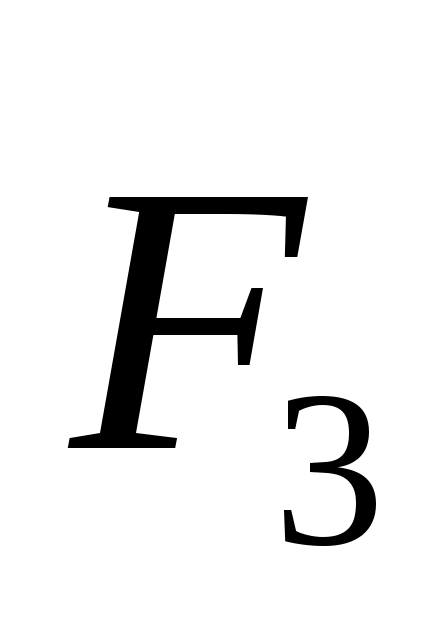 и и 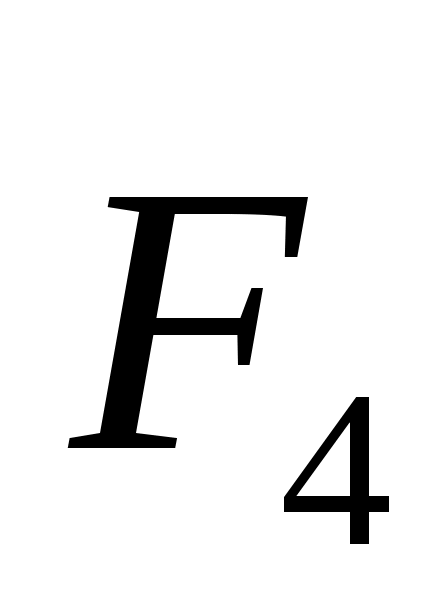 равна нулю. Определить модуль силы равна нулю. Определить модуль силы 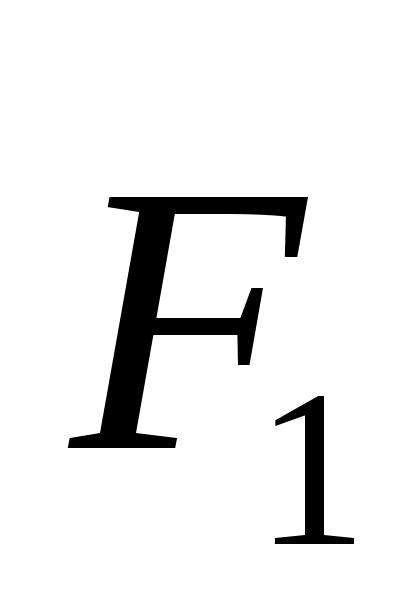 , если известны проекции трех других сил на оси координат: F2x = 4 Н, F2y = 7 Н; F3x = - 5 Н; F3y= - 5 Н; F4х = - 2H; F4y = 0. (3,61) , если известны проекции трех других сил на оси координат: F2x = 4 Н, F2y = 7 Н; F3x = - 5 Н; F3y= - 5 Н; F4х = - 2H; F4y = 0. (3,61)
2.1.14. Известны проекции на оси координат Rx = 18 Н и Rу= 24 Н равнодействующей 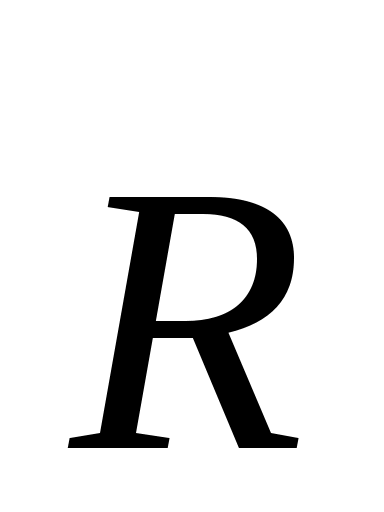 плоской системы сходящихся сил плоской системы сходящихся сил 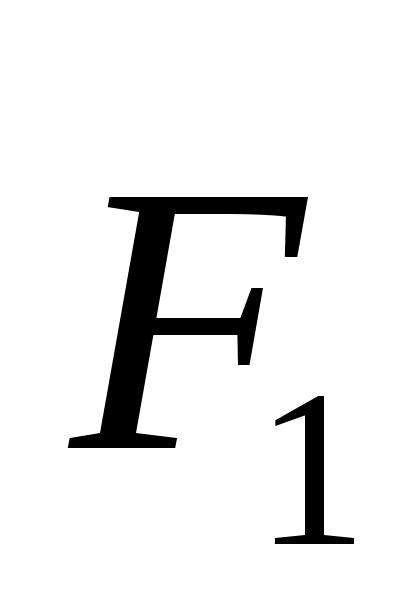 , , 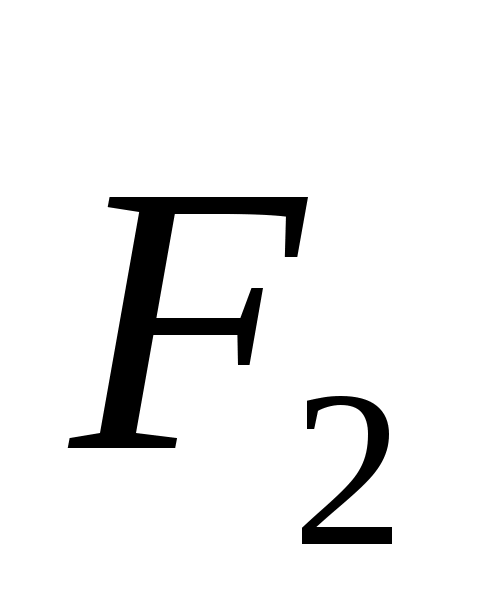 , и , и 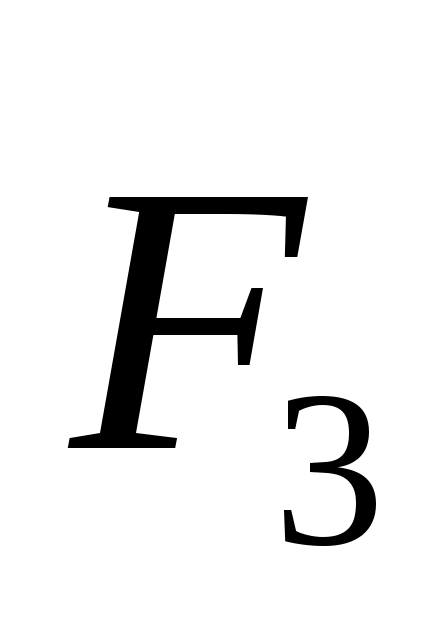 , а также проекции сил , а также проекции сил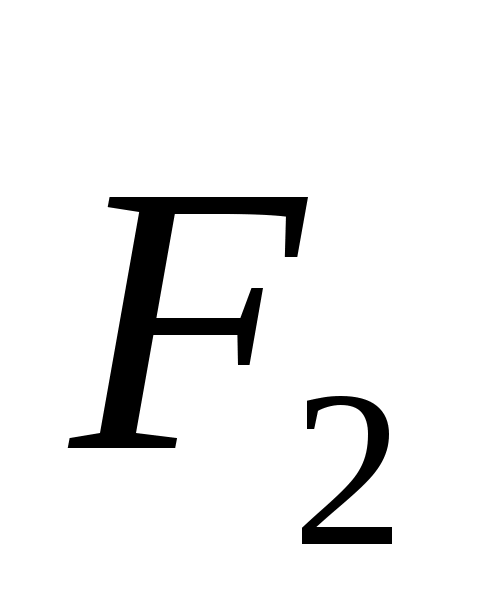 , и , и 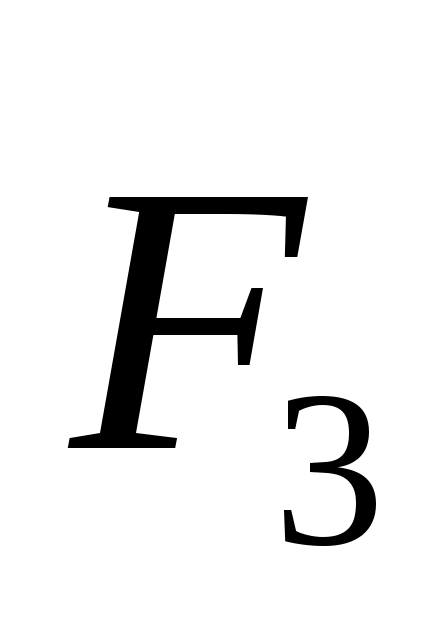 на эти же оси: F2x= - 9 Н, F2у = - 7 Н, F3x = 12 Н, F3у = 0. Определить модуль силы на эти же оси: F2x= - 9 Н, F2у = - 7 Н, F3x = 12 Н, F3у = 0. Определить модуль силы 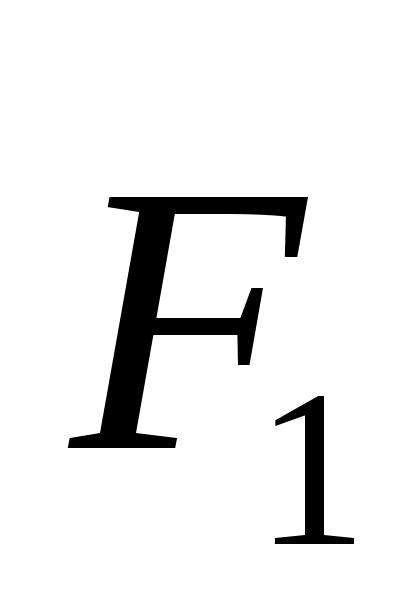 . (34,4) . (34,4)
2.1.15. Определить в градусах угол между вектором равнодействующей 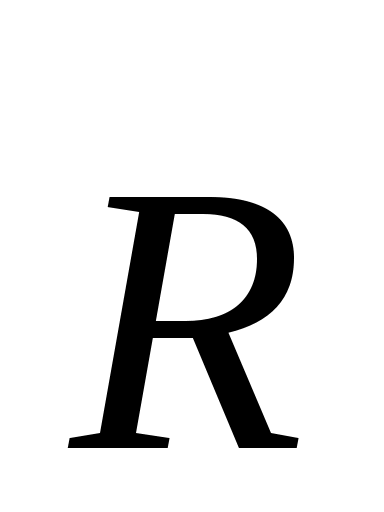 системы сил (Н) системы сил (Н) 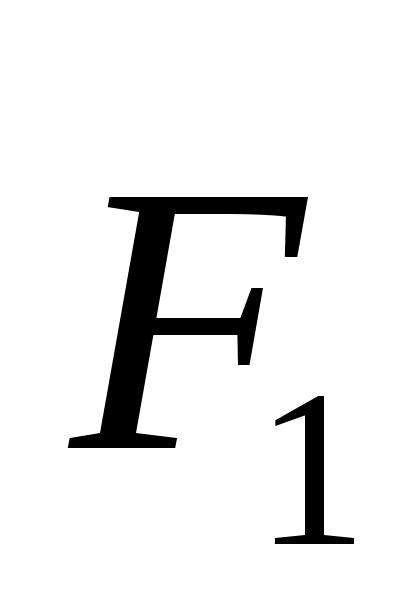 = 3 = 3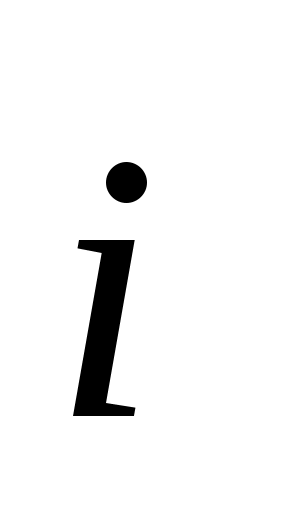 + 2 + 2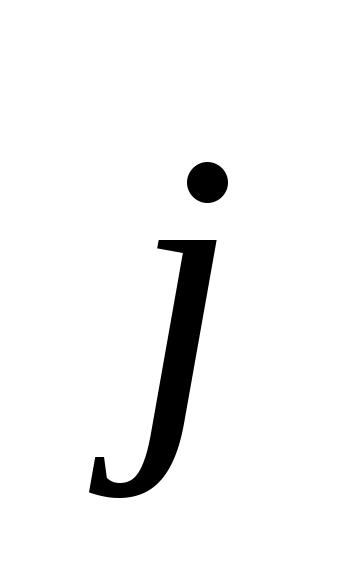 и и 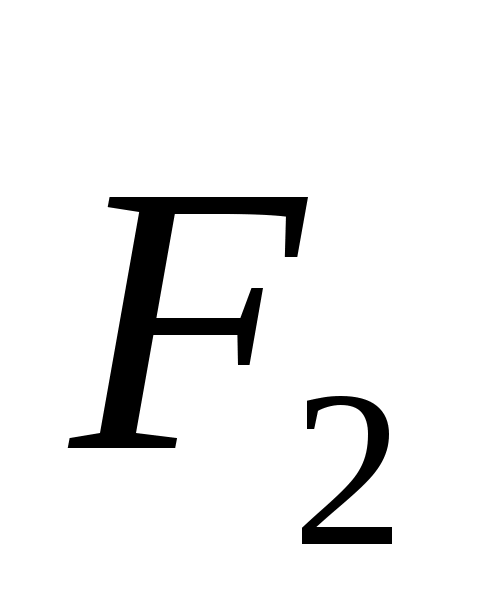 = 5 = 5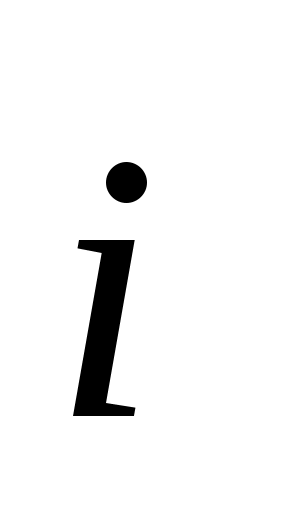 + 7 + 7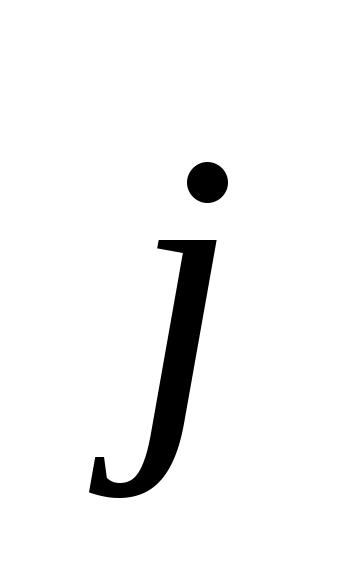 и положительным направлением оси Оу. (41,6) и положительным направлением оси Оу. (41,6)
Равновесие плоской системы сходящихся сил
2.1.16. Силы F1= F2 = 10 Н и 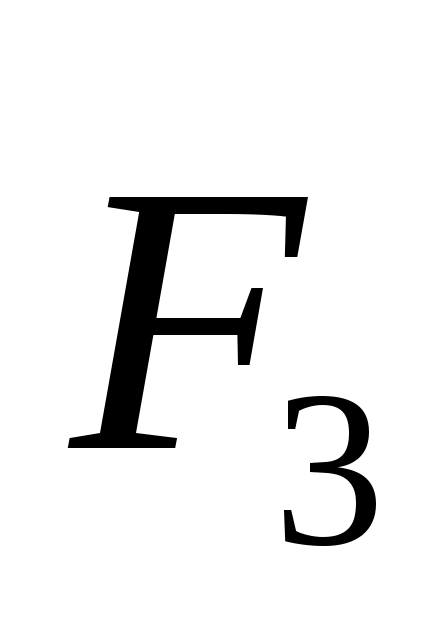 находятся в равновесии. Линии действия сил между собой образуют углы по 120°. Определить модуль силы находятся в равновесии. Линии действия сил между собой образуют углы по 120°. Определить модуль силы 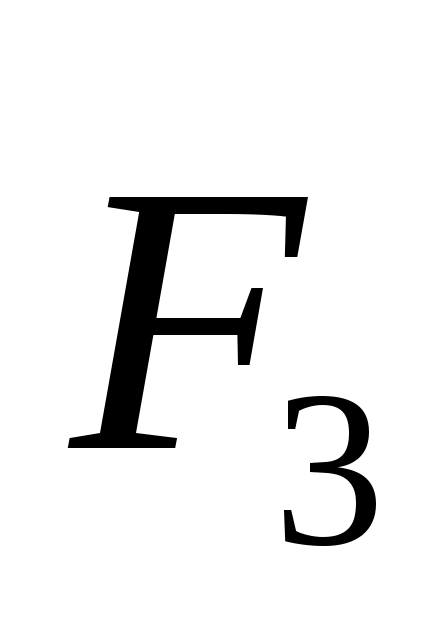 . (10) . (10)
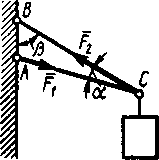
2.1.17. Определить модуль силы 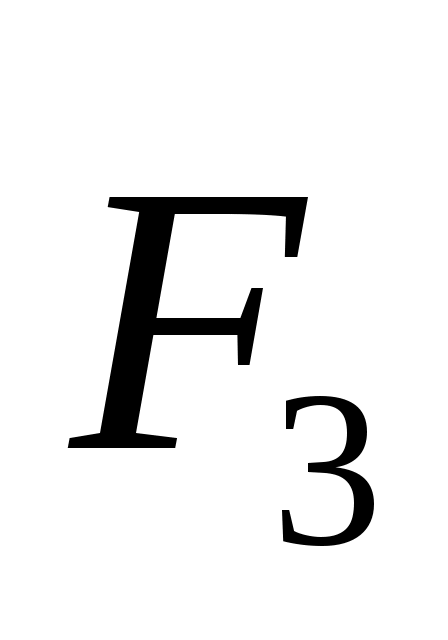 натяжения троса ВС (рис.186), если известно, что натяжение троса АС равно F2 = 15 Н. В положении равновесия углы α = 30° и β = 75°. (7,76) натяжения троса ВС (рис.186), если известно, что натяжение троса АС равно F2 = 15 Н. В положении равновесия углы α = 30° и β = 75°. (7,76)
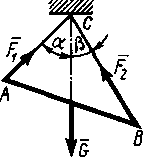
2.1.18. Определить вес балки АВ (рис. 187), если известны силы натяжения веревок Fl = 120 Н и F2 = 80 Н. Заданы углы α= 45° и β= 30° между вертикалью и веревками АС и ВСсоответственно. (154)
|
|
|
 Скачать 1.32 Mb.
Скачать 1.32 Mb.