Статика7. 2. статика в статике изучаются условия равновесия твердых тел под действием сил
 Скачать 1.32 Mb. Скачать 1.32 Mb.
|
Плоская система параллельных силПример. Система, состоящая из трех грузов М1, M2,M3 и блоков (рис. 198, а), находится в равновесии. Определить зависимость между весами грузов Р1, Р2, Р3 и 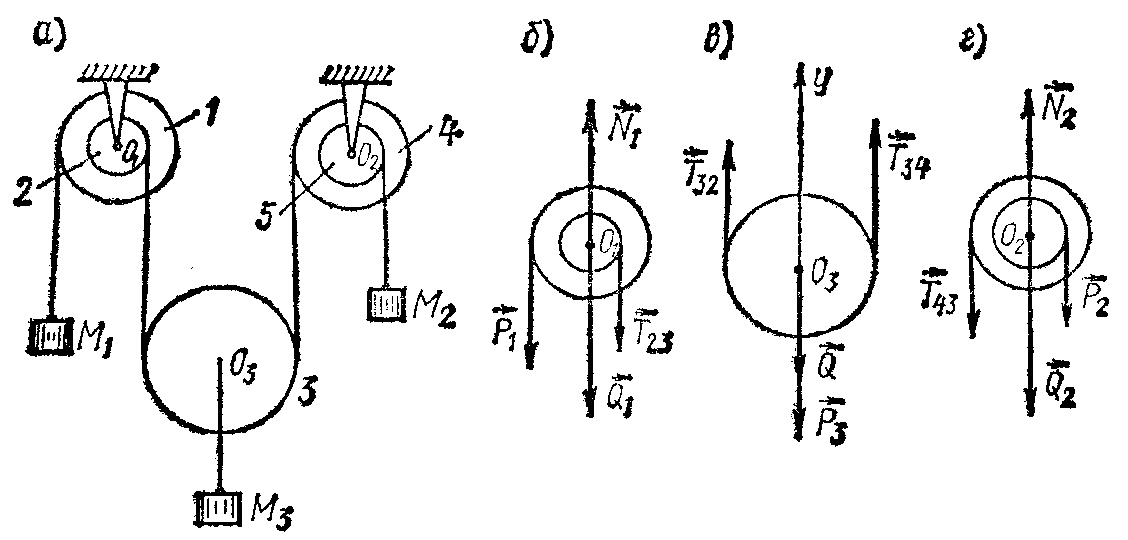 Рис. 198 силы в тросах, если вес блока 3 равен Q, радиусы блоков r1, r2, r3, r4, r5. Блоки 1 и 2, а также 4 и 5 попарно жестко соединены между собой. Решение. Система состоит из нескольких тел и находится в равновесии, следовательно, находятся в равновесии и блоки 1—2, 3, 4—5. Рассмотрим равновесие спаренных блоков 1—2 (рис. 198, б). Непосредственно приложенные силы: вес Реакция троса откуда Рассмотрим равновесие блока 3. Кроме веса груза Составим уравнения равновесия этого блока (рис. 198, в); Отсюда находим Рассмотрим равновесие спаренных блоков 4—5 (рис. 198, г). На них действуют вес груза отсюда Задачи Равновесие плоской системы параллельных сил 2.1.30. При расчете на изгиб поршневой палец рассматривается как балка, свободно лежащая на двух опорах (рис. 199). Определить модули реакций опор, принимая нагрузку интенсивностью q равномерно распределенной по длине l и расположенной симметрично относительно опор. Весом пальца пренебречь. О 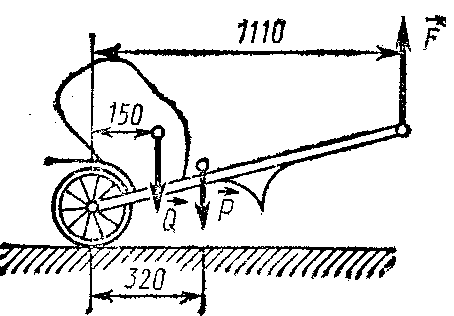 твет: RA= RB = ql/2. твет: RA= RB = ql/2.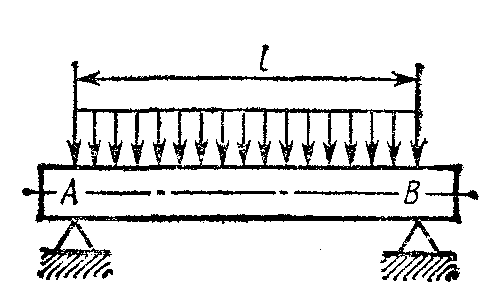 Рис. 199 Рис. 200 2.1.31. Определить модуль силы вертикальной силы Ответ: F = 152,3 H. На балку АВ действуют (рис. 201) вертикальная сила F = 5 кН и распределенная нагрузка интенсивностью q = 4 кН/м. Определить в кН реакцию опоры В, если длины АС = 3 м, ВС = 6 м. (2,0) 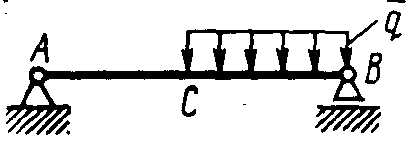 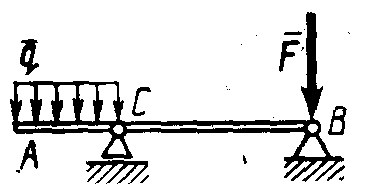 Рис. 201 Рис. 202 2.1.33. На однородную балку АВ (рис. 202), вес которой G = 20 кН, действует распределенная нагрузка интенсивностью q = 0,5 кН/м. Определить в кН реакцию опоры А, если длины АВ = 6 м, АС = ВС. (10,4) 2.1.34. На балку АВ (рис. 203) действуют силы F = 9 Н и распределенная нагрузка интенсивностью q = 3 кН/м. Определить реакцию опоры В, если длины АВ = 5м, ВС = 2 м. (10,2) 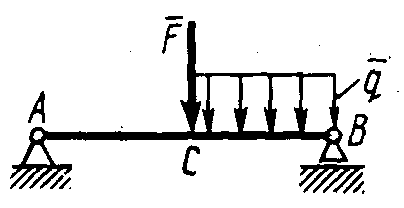 Рис. 203 Рис. 204 2.1.35. Какой должна быть длина участка АС (рис. 204)сдействующей на него распределенной нагрузкой интенсивностью q = 5 кН/м, для того чтобы реакция опоры В была равна 10 кН, если длина балки АВ = 9 м? (6,0) 2.1.36. Определить реакцию опоры С (рис. 205), если интенсивность распределенной нагрузки qmax= 120 Н/м, размеры АВ = 4,5м, ВС = 1,5 м. (135) 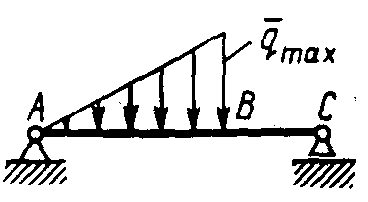 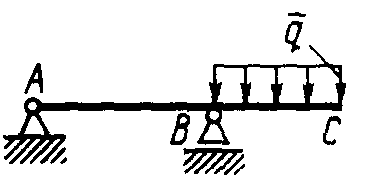 Рис. 205 Рис. 206 2.1.37. Определить реакцию опоры В (рис. 206), если интенсивность распределенной нагрузки q = 40 Н/м, размеры балки АВ = 4 м, ВС = 2 м. (100) 2.1.38. Какой должна быть интенсивность qmax распределенной нагрузки (рис. 207), для того чтобы реакция опоры В равнялась 200 Н, если размеры АС = 2 м, CD = 3 м, DB = 1 м? (200) 2 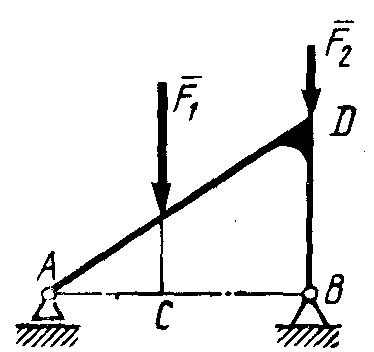 .1.39. На раму ADB (рис.208) действуют вертикальные силы F1= 9 кН и F2 = 4 кН. Определить в кН реакцию опоры В если расстояния АС = 2,5 м, АВ = 6м. (7,75) .1.39. На раму ADB (рис.208) действуют вертикальные силы F1= 9 кН и F2 = 4 кН. Определить в кН реакцию опоры В если расстояния АС = 2,5 м, АВ = 6м. (7,75) 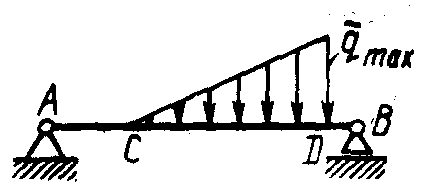 Рис. 207 Рис. 208 2 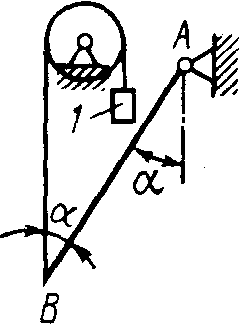 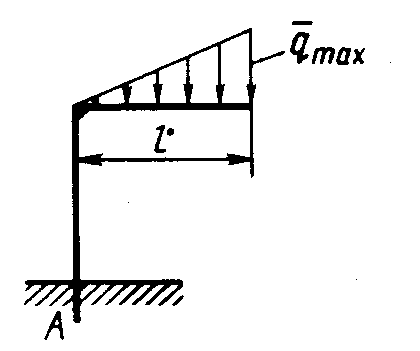 .1.40. Определить вес груза 1 (рис. 209) необходимый для того, чтобы однородная балка АВ весом 340 Н в положении равновесия была горизонтальна. (170) .1.40. Определить вес груза 1 (рис. 209) необходимый для того, чтобы однородная балка АВ весом 340 Н в положении равновесия была горизонтальна. (170)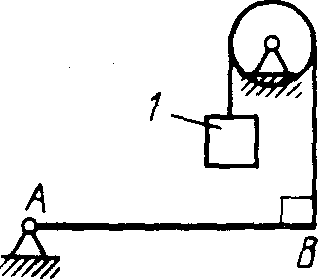 2 Рис. 209 Рис. 210 Рис. 211 2.1.41. Вес однородной балки АВ (рис. 210) равен 140 Н. Определить вес груза 1, необходимый для того, чтобы балка АВ находилась в равновесии в указанном положении. (70) 2.1.42. Определить длину l кронштейна (рис. 211), при которой момент в заделке МА = 3Н·м, если интен-сивность распределенной нагрузки qmax = 1 Н/м. (3,0) 2 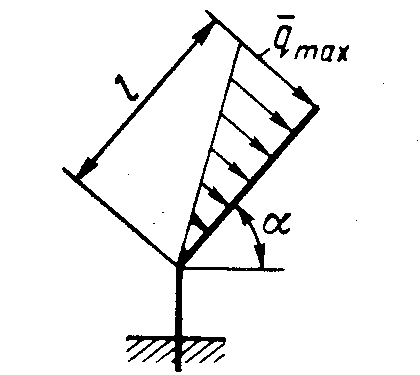 .1.43. На кронштейн (рис.212) действует распределенная нагрузка интенсивностью qmax = 4 Н/м. При каком значении угла αв градусах вертикальная составляющая реакции заделки в точке А равна 1 Н, если расстояние l =1 м? (60,0) .1.43. На кронштейн (рис.212) действует распределенная нагрузка интенсивностью qmax = 4 Н/м. При каком значении угла αв градусах вертикальная составляющая реакции заделки в точке А равна 1 Н, если расстояние l =1 м? (60,0) Рис. 212 |
