Статика7. 2. статика в статике изучаются условия равновесия твердых тел под действием сил

• Название: 2. статика в статике изучаются условия равновесия твердых тел под действием сил
• Дата: 06.04.2021
• Размер: 1.32 Mb.
• Имя файла: Статика7.doc
• Тип: Документы; #191778
• страница: 5 из 9

Равновесие произвольной плоской системы сил

2.1.44. На закрепленную балку действует произвольная плоская система сил. Сколько независимых уравнений равновесия балки можно составить? (3)

2.1.45. Определить реакцию опоры D (рис.213),если силы F₁ = 84,6 Н, F₂ = 208 Н, размеры АВ = 1 м, ВС = 3м, СО=2м. (130)

2.1.46. На балку (рис. 214), длина которой l = 3 м, дейст­вуют пары сил с моментами М₁= 2 кН·м и M₂= 8 кН·м. Определить в кН модуль реак­ции опоры В. (2,0)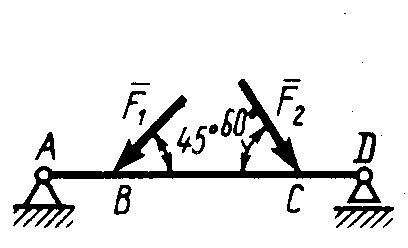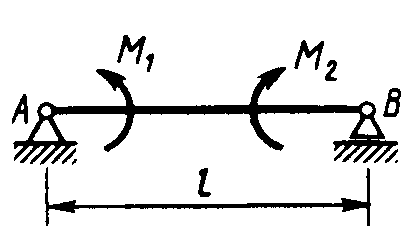




Рис. 213 Рис. 214

2.1.47. Определить момент М пары сил (рис. 215), при кото­ром реакция опоры В равна 250 Н, если ин­тенсивность распределенной нагрузки q = 150 Н/м, размеры АС = В = 2 м. (200)

2.1.48. На рычаг (рис. 216) действуют силы F₁ = 50 кН и . Определить в кН силу F₂, при которой рычаг в указанном положении находится в равновесии, если угол

α = 60°, а длины АО = 3 м, ОВ = ВС = 4 м. (65,0)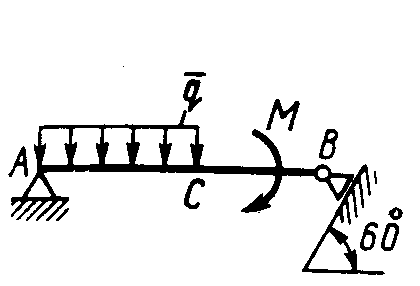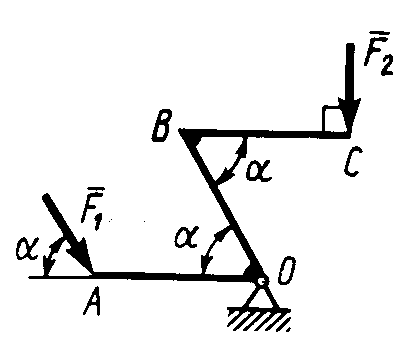


Рис. 215 Рис. 216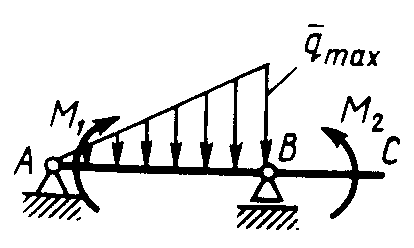

2.1.49. На балку АВ (рис.217) действуют распределенная нагрузка интенсивностью q = 2 Н/м и сила F = 6 Н Определить реакцию опоры В, если длина АС = '/з АВ, угол α = 45°. (4,08)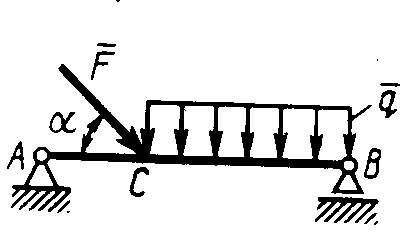



Рис. 217 Рис. 218

2.1.50. На балку АС (рис. 218) действуют распределенная нагрузка интенсивностью q_max= 2,5 Н/м и пары сил с моментами M₁ = 4 Н·м и М₂ = 2 Н·м. Определить реакцию опоры В, если длина АВ = 4 м, ВС = 0,5 АВ. (3,83)

2 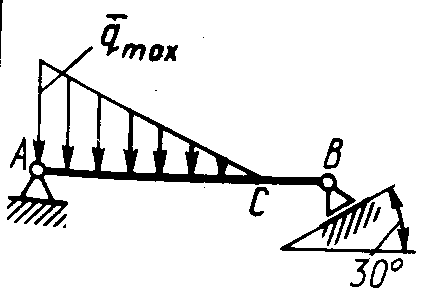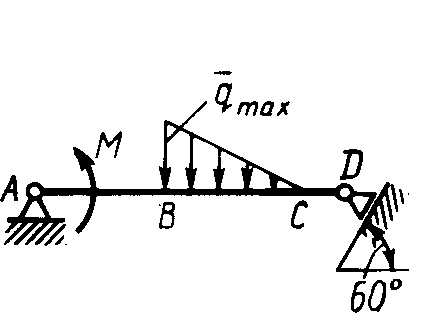.1.51. Определить интенсивность q_max распре­деленной нагрузки (рис. 219), при которой реакция шарнира В равна 346 Н, если размеры АВ = 8м, АС = 6м. (400)
Рис.219 Рис. 220

2.1.52. Определить реакцию опоры D в кН (рис. 220), если момент пары сил М = 13 кН·м, интенсивность распределенной нагрузки q_тах = 8 кН/м, размеры

АВ = ВС = 3 м, CD = 1 м. (10,0)

2 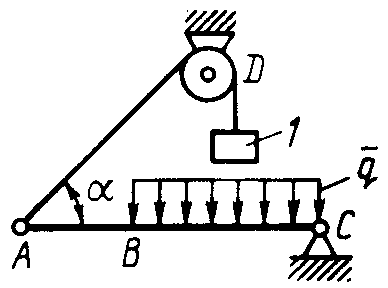.1.53. Балка АС закреплена в шарнире С и под­держивается в горизонтальном положении веревкой AD, перекинутой через блок (рис. 221). Опре­делить интенсивность распределенной нагруз­ки q, если длины ВС = 5 м, АС = 8 м, угол α = 45°, а вес груза 1 равен 20 Н. (9,05)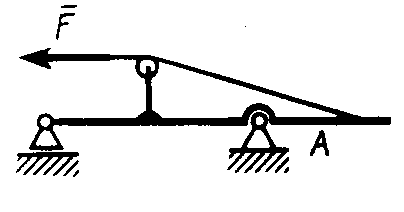



Рис. 221 Рис. 222

2.1.54. Определить вес груза 1, необходимый для удержания однородной балки АВ в равнове­сии в горизонтальном положении (рис.222), если ее вес равен 346 Н. (200)

2.1.55. Определить в кН горизонтальную состав­ляющую реакции неподвижного шарнира А балки (рис.223), если натяжение троса F = 35 кН. (35,0)

2.1.56. Определить реакцию опоры А рис.(224), если длина балки l = 0,3 м, интенсивность распределен­ной нагрузки q_тах= 20 Н/м, угол α = 60°. (2.0)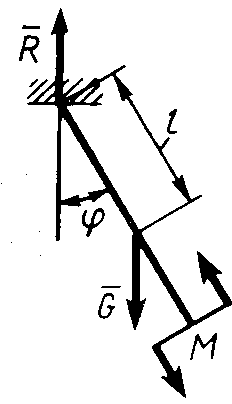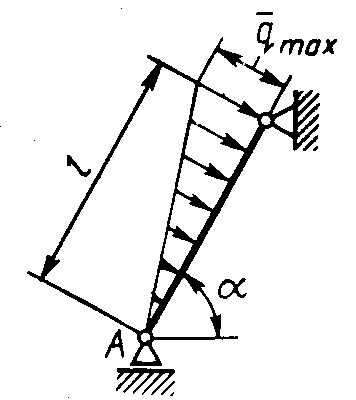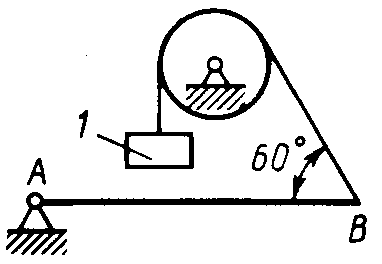





Рис. 223 Рис. 224 Рис. 225

2.1.57. Маятник находится в равновесии под дей­ствием пары сил с моментом

М 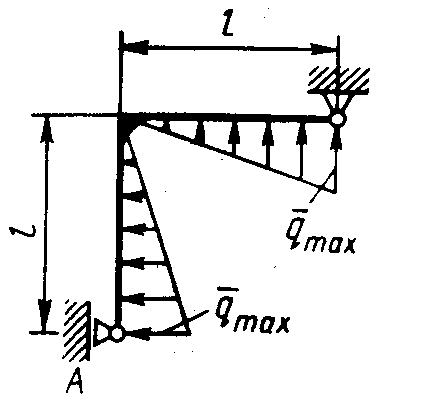= 0,5 Н·м и второй пары силы, образованной весом G и опорной реакцией R(рис.225). Найти значение угла φ отклонения маятника в градусах, если G = 10 Н и расстояние l = 0,1 м. (30,0)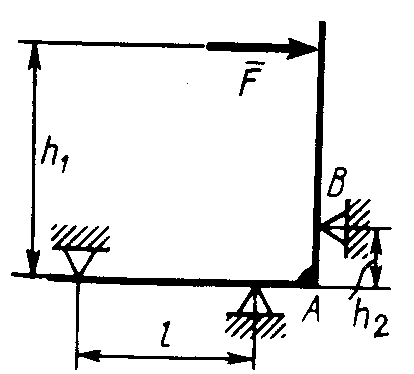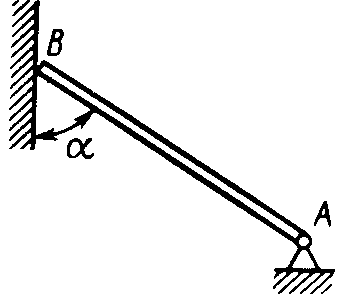




Рис.226 Рис. 227 Рис. 228

2.1.58. Конец В однородного бруса весом 100 кН (рис.226), закрепленного в шарнире А, опирается на глад­кую стену. Определить в кН давление бруса на стену, если угол α = 60°. (86,6)

2.1.59. На раму действует распределенная нагруз­ка интенсивностью q_mах=20 Н/м (рис.227). Определить реакцию опоры А, если размер l = 0,3 м. (3,0)

2.1.60. На угольник действует горизонтальная си­ла F (рис.228). На каком расстоянии h₂ надо поместить опору В, для того чтобы реакции опор А и В были одинаковы, если размеры l = 0,3 м, h₁ = 0,4м. (0,10)

2.1.61. Определить горизонтальную составляю­щую реакции опоры С горизонтальной балки АВ (рис. 229), если к ней подвешен груз 1 весом 18 кН. (0)

2.1.62. Стержень удерживается под углом α = 30° к горизонту (рис. 230). Определить реакцию опоры А, если момент пары сил М = 25 кН·м. (0)

2 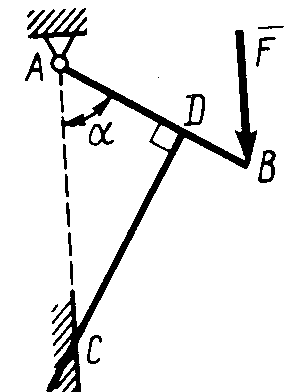.1.63. Балка АВ опирается на стержень CD(рис. 231). Опре­делить реакцию стержня CD, если длины АВ = 2 м, BD = '/зАВ, сила F = 4 Н, угол α = 60° . (5,20)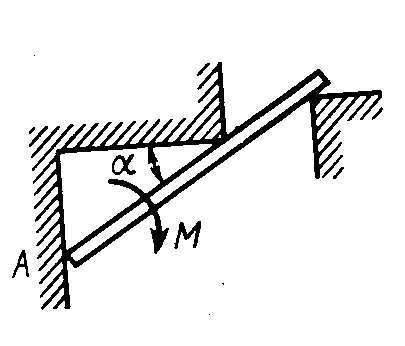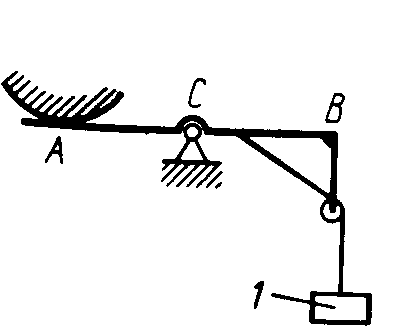






Рис. 229 Рис. 230 Рис. 231

2.1.64. На изогнутую балку АВ (рис. 232), заделанную в сте­ну, действуют распределенные нагрузки интен­сивностью q₁ = 5 Н/м и q₂= 3 Н/м. Опреде­лить момент заделки, если длины ВС = 3 м, AD = 5 м. (-60,0)

2.1.65. Определить горизонтальную силу F (рис. 233), при которой реакция опоры В арки АВ равна 200 Н, если размеры а = 1 м, АВ = 4 м. (693)

2 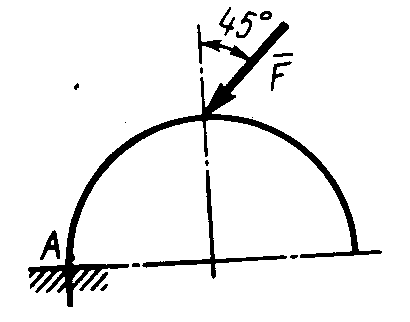.1.66. Арка, имеющая форму полуокружности (рис. 234), жестко заделана в точке А. Определить момент в заделке, если сила F = 100 Н. (0)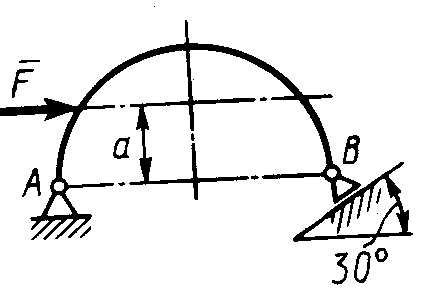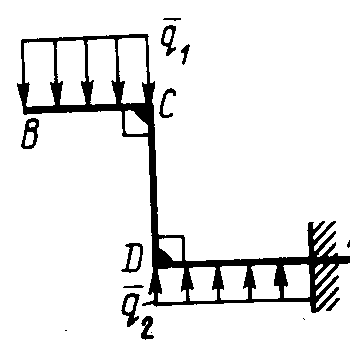




Рис. 232 Рис. 233 Рис. 234

2.1.67. Грузы 1 и 2 висят на канатах, намотанных на ступенчатый барабан (рис. 235). Определить в кН гори­зонтальную составляющую реакции шарнира А, если угол α = 60°, вес груза 1 равен 30 кН. Система находится в равновесии. (15,0)

2.1.68. Грузы 1 и 2 висят на канатах (рис. 236), намотанных на ступенчатый барабан. Определить в кН вер­тикальную составляющую реакции шарнира А, если радиус R = 2r, угол α = 30°, вес груза 1 равен 20 кН. Система находится в равновесии. (50,0)

2.1.69. Стержень АВ жестко связан с диском (рис. 237). Определить в кН реакцию опоры В, если сила

F = 24 кН, угол α = 30°. (6,0)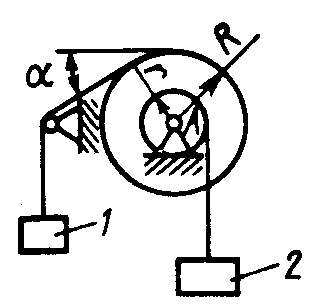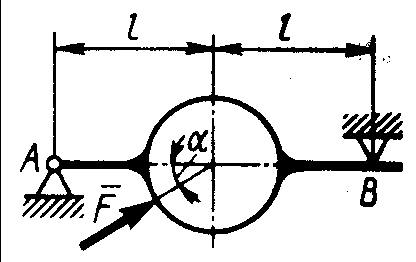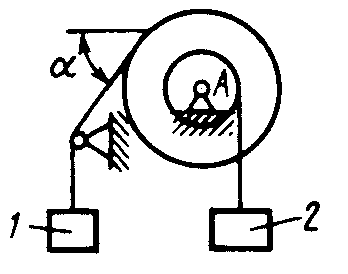




Рис. 235 Рис. 236 Рис. 237

2.1.70. Стержень АС жестко связан с рамой (рис. 238). Оп­ределить в кН реакцию опоры В, если силы F₁= F₂= 20 кН, момент пары сил М = 80 кН·м, расстояние l = 2 м. (50,0)

2 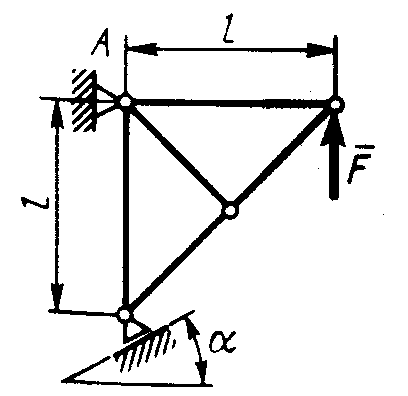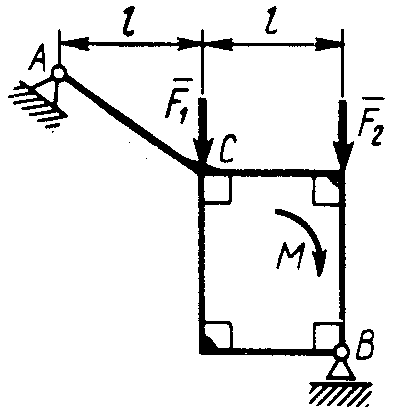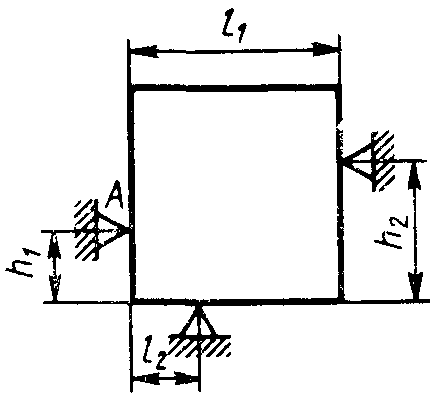.1.71. На ферму действует вертикальная сила F (рис. 239). При каком значении в градусах угла α реакция опоры R_А = 2 F? (30,0)
Рис. 238 Рис. 239 Рис. 240
2.1.72. Однородная квадратная пластина весом 1 Н закреплена в вертикальной плоскости на трех опорах (рис. 240). Определить реакцию опоры А,если размеры

l₁ = 0,3 м, l₂= 0,1 м,h₁ = 0,1 м, h₂ = 0,2 м. (0,50)

2 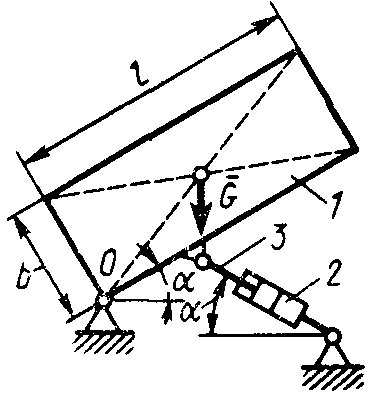.1.73. Лестница 1 (рис. 241) весом G = 2 кН удерживается в горизонтальном положении с помощью силового гидроцилиндра 2. Определить в кН силу, действующую на шток 3 гидроцилиндра, если момент силы М_О(G) = 2 кН·м, угол α = 30°, расстояние АО = АВ = 0,5 м. (2,93)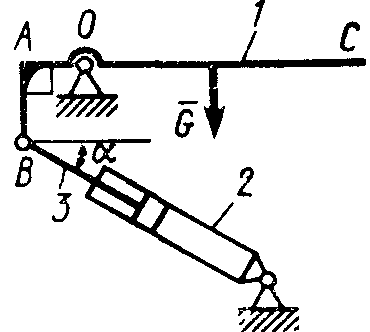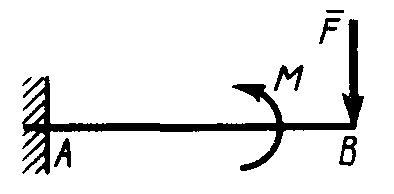






Рис. 241 Рис. 242 Рис. 243

2.1.74. Кузов 1 весом G = 10 кН удерживается в равновесии силовым гидроцилиндром 2 (рис. 242). Опре­делить в кН силу, действующую на шток 3 гид­роцилиндра, если расстояния l = 3 м, a = 1,2 м, АО = 1 м и угол α = 30°. (11,5)

2.1.75. На консольную балку АВ (рис. 243), заделанную в стену, действуют сила F = 4 Н и пара сил с мо­ментом М = 2 Н·м. Определить момент в заделке, если длина АВ = 4 м. (14,0)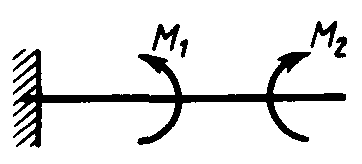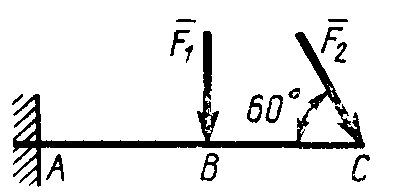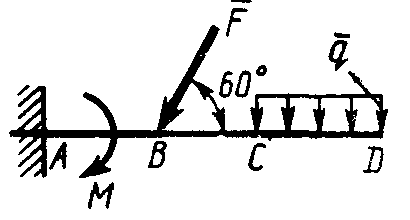



Рис. 244 Рис. 245 Рис. 246

2.1.76. Консольная балка (рис. 244) нагружена парами сил с моментами M₁ =1790 Н·м и М₂= 2135 Н·м. Определить момент в заделке. (-345)

2.1.77. К балке AD (рис.245) приложена пара сил с момен­том М = 200 Н·м, распределенная нагрузка интенсивностью q = 20 Н/м и сила F. Какой должна быть эта сила, для того чтобы момент в заделке А равнялся 650 Н·м, если размеры AB = BС =CD = 2м? (144)

2.1.78. Определить момент в заделке А (рис. 246), если F₁ = 50 Н, F₂ = 100 Н, размеры АВ = ВС = 2 м. (446)

2.1.79. Определить интенсивность q распределен­ной нагрузки (рис. 247), при которой момент в заделке А равен 546 Н·м, если сила F =173 Н, мо­мент пары сил

М 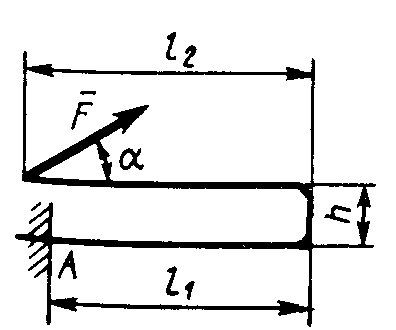= 42 Н·м, размеры АВ = CD = 2 м, ВС = 1 м. (36,0)


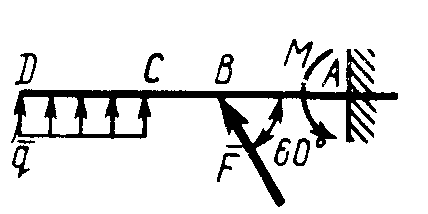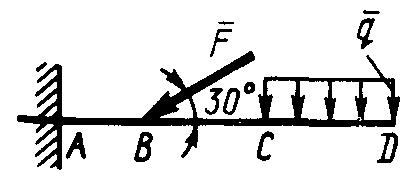Рис. 247 Рис. 248 Рис. 249

2 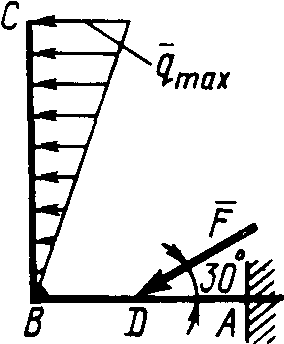.1.80. Определить силу F (рис. 248), при которой момент в заделке А равен 3700 Н·м, если интенсив­ность распределенной нагрузки q = 200 Н/м, размеры АВ = ВС = 2 м, CD = 3 м. (400)

2.1.81. Определить в кН·м момент в заделке А (рис. 249),если сила F = 80 кН, угол α = 30°, расстояния l₁= 1,8 м, l₂ = 2 м, Рис. 250 h = 0,4 м. (35,7)

2.1.82. Определить модуль момента в заделке А (рис. 250),если сила F = 150 Н, интенсивность q_max рас­пределенной нагрузки равна 40 Н/м, размеры ВС = 3м.

AD = BD = 1м,(195)