Статика7. 2. статика в статике изучаются условия равновесия твердых тел под действием сил

• Название: 2. статика в статике изучаются условия равновесия твердых тел под действием сил
• Дата: 06.04.2021
• Размер: 1.32 Mb.
• Имя файла: Статика7.doc
• Тип: Документы; #191778
• страница: 6 из 9

Равновесие тела с учетом трения скольжения

2.1.83. На наклонной плоскости лежит груз. Определить в градусах максимальный угол наклона плоскости к горизонту, при котором груз останется в покое, если коэффициент трения скольжения равен 0,6. (31)

2.1.84. Каким должен быть наименьший вес тела 2 (рис.251), для того чтобы тело 1 весом 200 Н начало скользить по горизонтальной плоскости, если коэффициент трения скольжения f = 0,2. (40,0)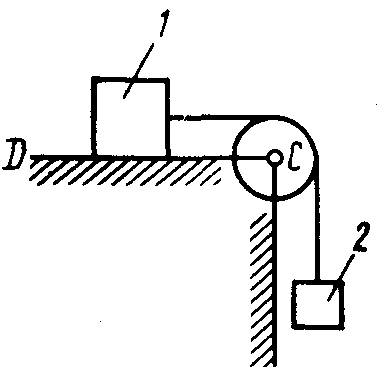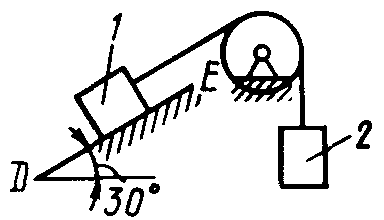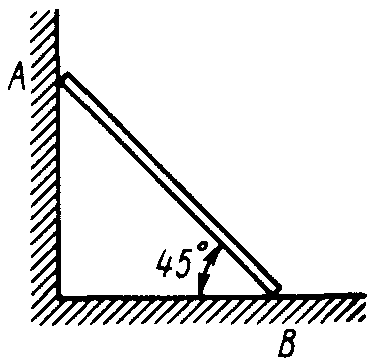


Рис. 251 Рис. 252 Рис.253

2.1.85. Определить наименьший вес тела 1, при котором оно скользит вниз по плоскости DE(рис. 252),если вес груза 2 равен 320 Н, коэффициент трения сколь-жения между телом 1 и плос­костью DE равен 0,2. (979)

2.1.86. Однородный брус АВ (рис. 253) опирается в точке А на гладкую стену, а в точке В на негладкий пол. Определить наименьший коэффициент трения скольжения между брусом и полом, при котором брус останется в указанном поло­жении в покое. (0,50)

2.1.87. Определить наименьший коэффициент тре­ния скольжения между грузом 1 весом 400 Н и плоскостью DC(рис. 254), при котором груз 1 оста­нется в покое, если вес груза 2 равен 96 Н. (0,24)

2.1.88. Определить наименьший вес груза 1(рис. 255), при котором он останется в покое, если вес груза 2 равен 140 Н, а коэффициент трения скольже­ния между грузом 1 и плоскостью равен 0,2. (700)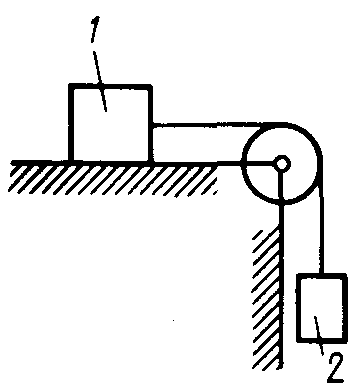

2.1.89. Каким должен быть вес тела 1(рис. 256), для того чтобы началось скольжение вверх по наклон­ной плоскости, если сила F = 90 Н, а коэффи­циент трения скольжения f = 0,3? (118)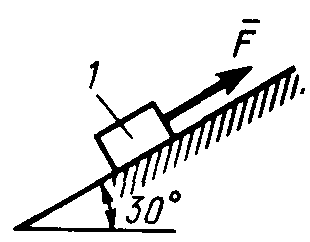







Рис. 254 Рис. 255 Рис. 256

2 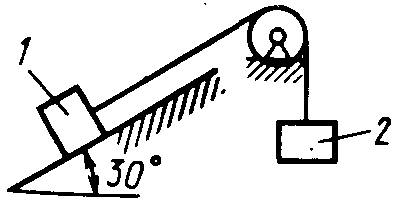.1.90. Каким должен быть наибольший вес груза 2 (рис.257), для того чтобы груз 1 весом 100 Н оставал­ся в покое на наклонной

Рис. 257 плоскости, если коэффициент трения скольжения f = 0,3? (76,0)

Равновесие тела с учетом трения качения

2.1.91*. Определить модуль горизонталь­ной силы , под действием которой тележка весом G движется равномерно по рельсовому пути (рис. 258), если веса всех колес равны Q, их ра­диусы R,а коэффициент трения качения колес о рельсы равен k. Принять АО=ОВ.

Ответ:

2.1.92*. Катушка радиусом R и весом Р находится в равновесии на горизонтальной плоскости (рис. 259). На среднюю цилиндрическую часть катушки радиусом rнамотана нить, переброшенная через идеальный блок А и несущая на своем конце груз D весом Q. Участок нити АВ составляет с вертикалью угол α. Определить момент сил трения качения и реакцию плоскости в точке каса­ния С.

О 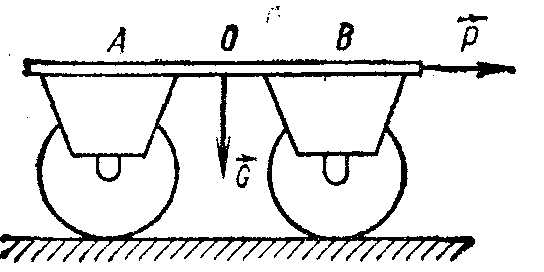твет: M = Q(R sinα - r) (при М > 0 пара трения качения стремится вращать катушку против хода часовой стрелки); Х_С = - Qsin α; Y_С = Р -Q cos α.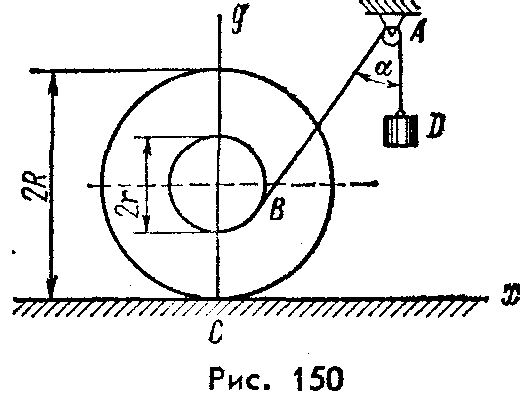


Рис. 258 Рис. 259

2.1.93. Цилиндр весом 520 Н лежит на горизон-тальной плоскости. Опре­делить наименьший модуль момента пары сил, необходимый для качения цилиндра. Коэффициент трения качения δ = 0,007 м. (3,64)

2.1.94. К однородному катку (рис. 260) весом 700 Н прило­жена сила . Определить наименьший модуль этой силы, для того чтобы каток начал ка­титься со скольжением, если радиус R = 1 м, коэффициенты трения скольжения и качения соответственно равны: f= 0,2, δ = 0,008 м. (183)

2.1.95. На однородный каток (рис. 261) весом 2 кН дейст­вуют горизонтальная сила F₂ = 10 Н и верти­кальная сила F₁. Каким должен быть наиболь­ший модуль силы F₁, для того чтобы началось качение катка, если коэффициент трения ка­чения δ = 0,005 м, радиус R = 0,8 м, размер А = 0,4 м? (400)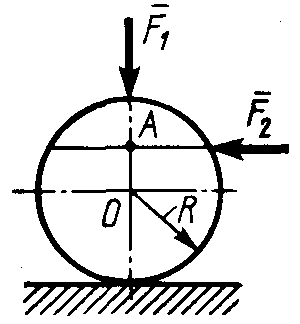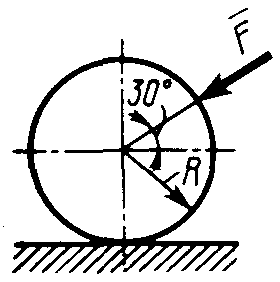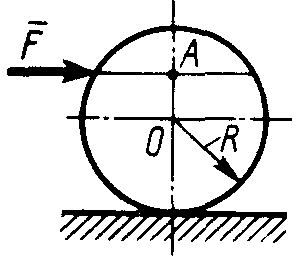



Рис. 260 Рис. 261 Рис. 262

2.1.96. К однородному катку (рис. 262) весом 2 кН прило­жена горизонтальная сила F. Определить наи­больший модуль силы F, при котором каток не скользит и не катится, если коэффициент трения качения δ = 0,006 м, коэффициент трения скольжения f = 0,2, радиус R = 0,6 м, размер ОА = 0,4м. (12,0)

2.1.97. К катку 1 (рис. 263) с помощью нерастяжимой нити подвешен груз 2. Определить наибольший вес этого груза, при котором каток 1 весом 3,2 кН останется в покое, если коэффициент трения качения δ = 0,004 м, радиус R = 32,4 см. (40,0)

2.1.98. К однородному катку 1 (рис. 264) весом 5 кН при­ложена пара сил с моментом М = 210 Н·м. Определить, каким должен быть наибольший вес груза 2, для того чтобы каток катился влево, если коэффициент трения качения δ = 0,003 м, радиус R = 0,453 м. (428)

2.1.99. Однородный каток 2 весом 4 кН связан с телом 1 нерастяжимой нитью (рис. 265). Радиус R = 0,5 м, коэффициент трения качения δ = 0,005 м, момент пары сил М = 50 Н·м. Определить наибольший вес тела 1, при котором оно начнет скользить, если коэффициент трения скольжения для катка и тела f = 0,2. (150)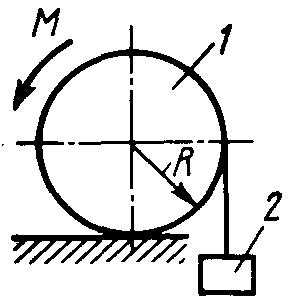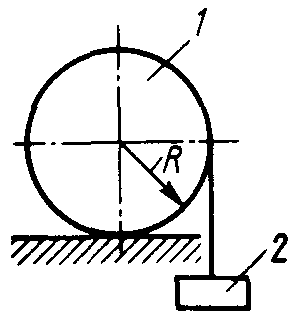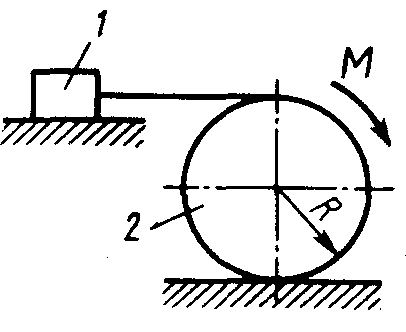



Рис. 263 Рис. 264 Рис. 265

2.1.100. Определить наименьшую силу F (рис. 266), необхо­димую для качения катка радиуса R = 0,3 м, если предельный момент трения качения равен 3,46 Н·м, угол

α 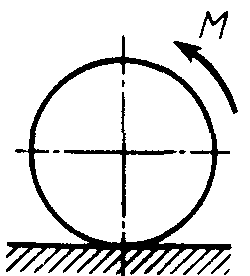= 30°, расстояние ОА = 0,2 м. (7,99)



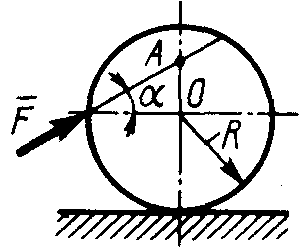Рис. 266 Рис. 267 Рис. 268

2.1.98. К однородному катку радиуса R = 0,4 м (рис. 267) приложена горизонтальная сила F=12 Н. Каким должен быть наименьший вес катка в кН, для того чтобы он находился в покое, если коэффициент трения качения δ = 0,008 м, размер ОА = 0,2 м? (0,9)

2.1.99. К однородному катку весом 4 кН (рис. 268) прило­жена пара сил с моментом М = 20 Н·м. Опре­делить наименьший коэффициент трения каче­ния, при котором каток находится в покое. (5.10^-3)

2.1.100. К однородному катку весом 4 кН (рис. 269) прило­жена горизонтальная сила F = 50 Н и пара сил с моментом М = 20 Н·м. Определить наимень­ший радиус R катка, при котором он будет катиться влево, если коэф-фициент трения качения δ = 0,005 м и ОА = 0,6R. (0,50)

2.1.101. К однородному катку, малый радиус которого 0,2 м (рис. 270), подвешен груз 1 весом 200 Н и приложена пара сил с моментом М = 57,6 Н·м. Определить в кН наибольший вес катка, при котором он будет катиться влево, если коэффициент трения качения δ = 0,008 м. (2,0)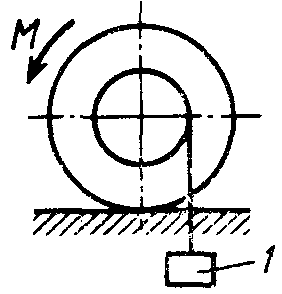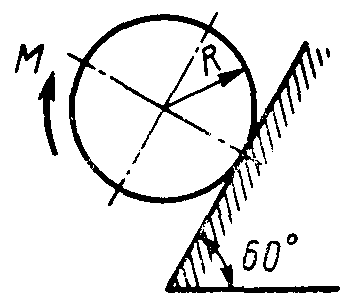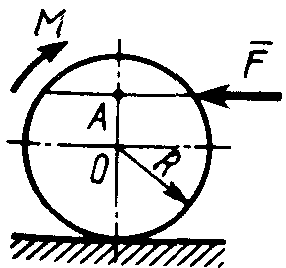



Рис. 269 Рис. 270 Рис. 271

2.1.102. К однородному катку (рис.271) радиуса R = 0,4 м приложена пара сил с моментом М = 210 Н·м. Каким должен быть наибольший вес катка, для того чтобы он мог катиться вверх по наклонной плоскости, если коэффициент тре­ния качения δ = 0,006 м? (601)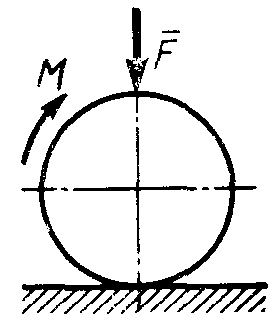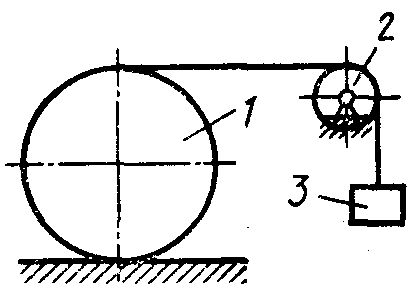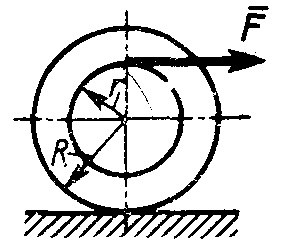



Рис. 272 Рис. 273 Рис. 274

2.1.103. Однородный каток (рис. 272), к которому приложе­на пара сил с моментом М = 18 Н·м, прижи­мается к опорной плоскости силой F= 600 Н. Каким должен быть наибольший вес катка в кН, при котором он будет катиться, если коэффициент трения качения δ = 0,006 м. (2,40)

2.1.104. Однородный каток 1 весом 10 кН и ради­усом 0,5м (рис. 273) связан с грузом 3, вес которого равен 80 Н, горизонтальной нерастяжимой нитью, перекинутой через блок 2. Определить наименьший коэффициент трения качения, при котором каток останется в покое. (0,008)

2.1.105. На конец кабеля (рис. 274), намотанного на барабан, действует сила F = 20 Н. Барабан катится рав­номерно по горизонтальной плоскости без скольжения. Определить в кН вес барабана, если его радиусы r = 0,5 м и R = 1 м. Коэф­фициент трения качения барабана δ = 0,01 м. (3,0)

2.2. РАВНОВЕСИЕ СИСТЕМЫ ТЕЛ ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ

2.2.1. Статическая определимость системы тел

2.2.1. Сколько независимых неизвестных величин можно определить для статически определимой системы трех тел, находящихся под дей­ствием плоской системы сил? (9)

2.2.2. Укажите номер статически определимой конструкции. (2)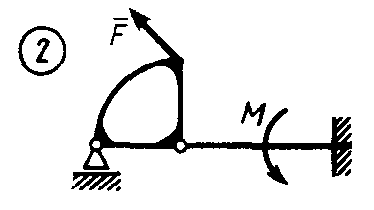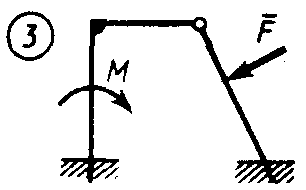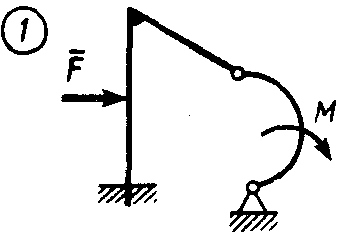



2.2.3. Укажите номер статически определимой конструкции. (1)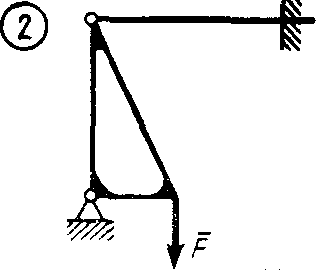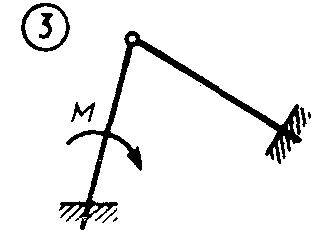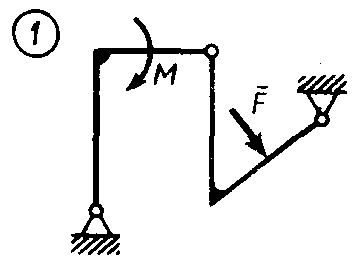




2.2.4. Укажите номер статически определимой конструкции. (3)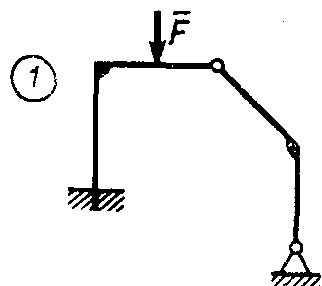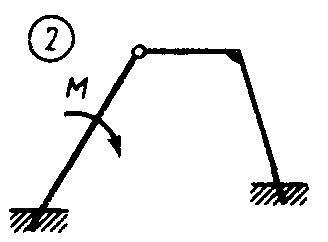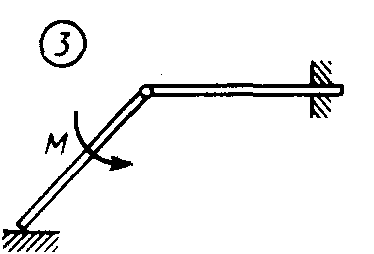



2.2.5. Укажите номер статически определимой конструкции. (2)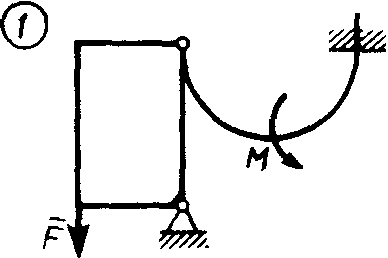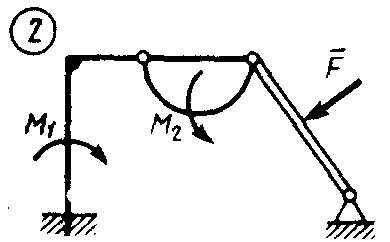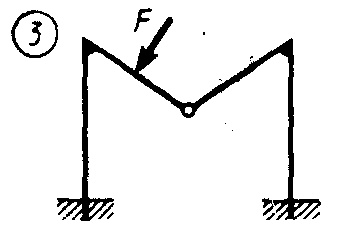




2 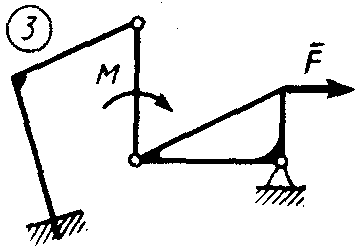.2.6. Укажите номер статически определимой конструкции. (3)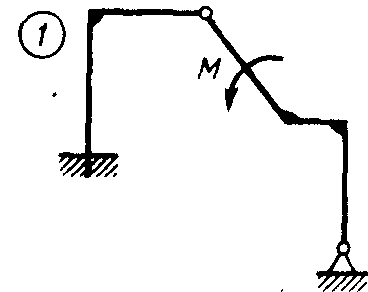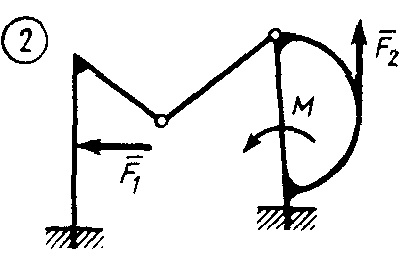




2.2.7. Укажите номер статически определимой конструкции. (1).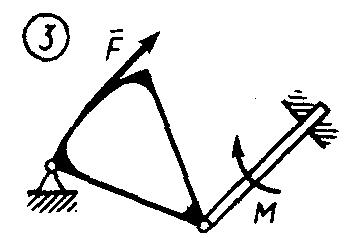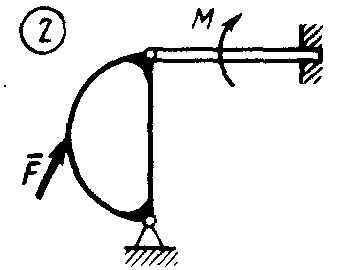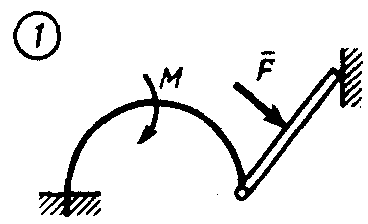




2 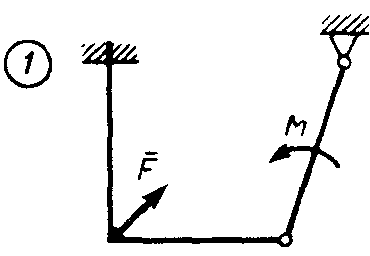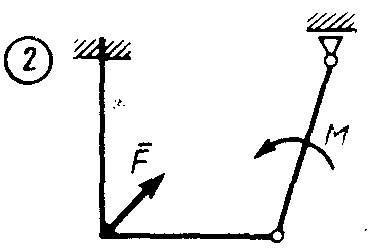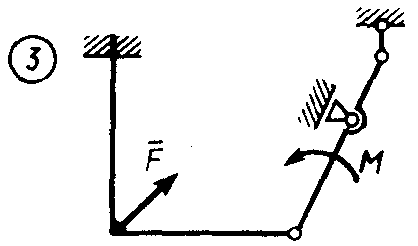.2.8. Укажите номер статически определимой системы(2).

2.2.9. Укажите номер статически неопределимой системы. (3)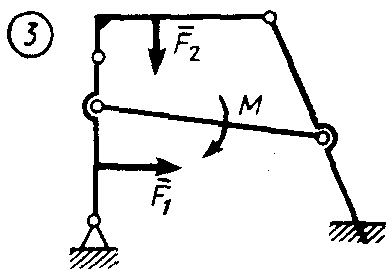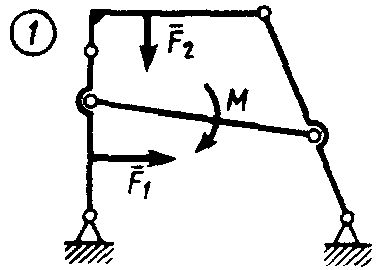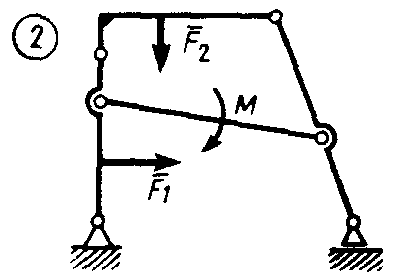




2.2.2. Равновесие статически определимой системы тел

2.2.10. Сколько независимых уравнений равновесия можно составить для системы четырех тел, находящихся в равновесии под действием плоской системы сил? (12)

2.2.11. Система тел (рис. 275) состоит из стержней ОА, АВ и троса ВС. Какое минимальное число уравнений равновесия необходимо составить для опреде­ления реакций в заделке О, шарнире А и тро­се ВС? (6)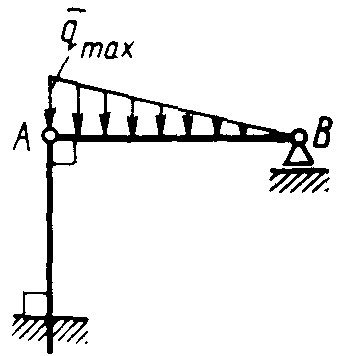

2.2.12. На балку АВ (рис. 276) действует пара сил с момен­том М = 800 Н·м. Определить момент в за­делке С, если АВ = 2 м и ВС = 0,5 м. (200)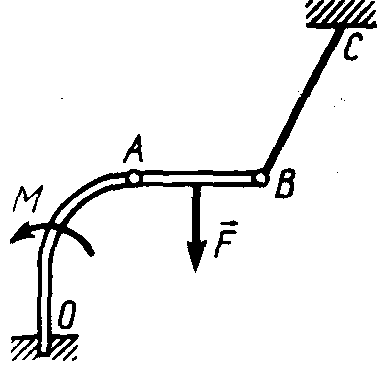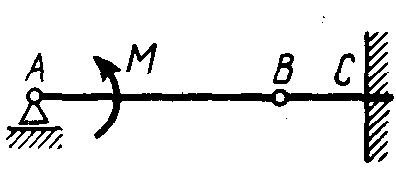





Рис. 275 Рис. 276 Рис. 277

2.2.13. На балку АВ (рис. 277) действует линейно распреде­ленная нагрузка интенсивностью q_max= 3 кН/м. Определить реакцию опоры В в кН, если расстояние

АВ = 2 м. (1)

2 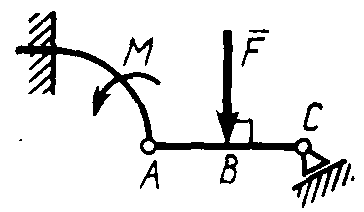.2.14. Определить реакцию опоры А в кН (рис. 278), если сила F = 3 Н, угол α = 30°, размеры АВ = ВС. (3)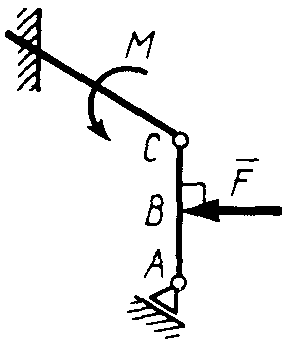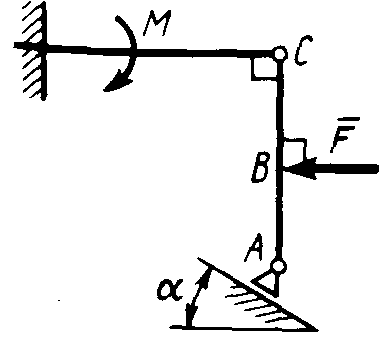



Рис. 278 Рис. 279 Рис. 280

2.2.15. Найти вертикальную составляющую реак­ции в шарнире А (рис. 279), если сила F = 900 Н, раз­меры АВ = ВС. (450)

2.2.16. Найти горизонтальную составляющую реакции в шарнире С (рис. 280), если сила F = 800 Н, размеры АВ = ВС. (400)

2.2.17. Стержни АВС и CD соединены между со­бой шарниром С (рис. 281). На стержень CD действует пара сил с моментом М = 400 Н·м. Опреде­лить составляющую реакции шарнира С,если длина CD = 2 м. (200)

2.2.18. Два стержня соединены в шарнире В (рис.282). Определить момент в заделке А, если силы

F ₁= 60H, F₂= 50Н. (240)


Рис. 281 Рис. 282 Рис. 283

2.2.19. Определить вертикальную составляющую реакции в шарнире А (рис. 283). (110)

2.2.20. Определить вертикальную составляющую реакции в шарнире В (рис. 284), если сила F = 850 Н, а размеры DC = СЕ = BE. (401)

2.2.21. Определить в кН·м момент М пары сил (рис. 287), при котором вертикальная составляющая ре­акции опоры А равна 10 кН, если размеры ВС=СЕ=1 м. (25,8)

2.2.22. Определить в кН силу F (рис. 286), при которой вер­тикальная составляющая реакции в шарнире А равна 9 кН, если размеры АВ = BD = 1 м, СЕ = DE, момент пары сил М = 6 кН·м. (4)



Рис. 284 Рис. 285 Рис. 286

2.2.23. Найти вертикальную составляющую реак­ции в шарнире С (рис.287), если сила F = 600 Н, разме­ры ВС = 2АВ. (200)

2.2.24. Найти вертикальную составляющую реак­ции в шарнире С (рис. 288), если к горизонтальному стержню АС приложена сила F₁ = 800 Н, к стержню CD — сила F₂, угол α = 30°, размеры АВ = ВС. (200)

2.2.25 Стержень АВ, длина которого 2 м (рис. 289), нагру­жен равномерно распределенной нагрузкой интенсивностью q = 100 Н/м. Определить реакцию опоры А. (141)


Рис. 287 Рис. 288 Рис. 289

2 .2.26. На конце однородного стержня АВ весом 80 Н с помощью шарнира В установлен одно­родный диск весом 200 Н (рис. 290). Диск опирается на вертикальную гладкую стену. Определить силу воздействия диска на стену. (240)




Рис. 290 Рис. 291 Рис. 292
2.2.27. Определить усилие в стержне 1 в случае равновесия системы (рис. 291), если вес тела 2 равен 100 Н. Весом остальных частей конструкции пренебречь. (905)

2 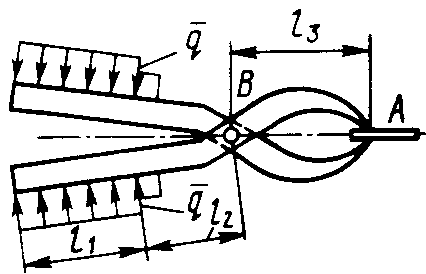.2.28. Определить в кН модуль силы F (рис. 292), при кото­рой момент в заделке А столба 2 равен нулю, если вес тела 1 равен 10 кН. Весом остальных элементов

конструкции пренебречь. (21,4)

Рис. 293

2.2.29. К щипцам (рис. 293) приложена равномерно распре­деленная нагрузка интенсивностью q = 5 кН/м. Определить вертикальную составляющую силы в кН, действующей на сжимаемый предмет, если размеры l₁ = 6 см, l₂ = 10 см, l₃ = 2 см.(1,95)

2.2.3. Равновесие плоских механизмов

2.2.30. Укажите максимальное число независимых неизвестных для механизма, состоящего из двух тел и находящегося в равновесии под действием плоской системы сил? (6)

2 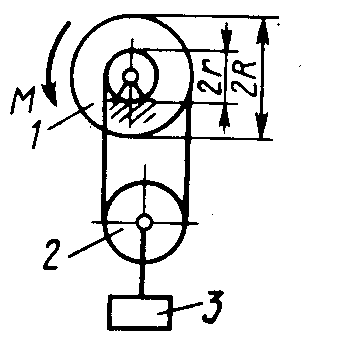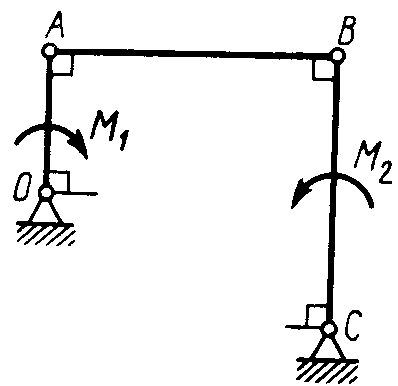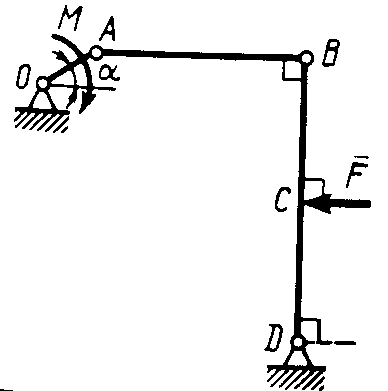.2.31. Определить момент М пары сил (рис. 294), который необходимо приложить к барабану 1 диффе­ренциального ворота для равномерного подъ­ема груза 3 весом 2·10³ Н, если радиусы R= 15 см и r =10 см. Весом блока 2 пренебречь. (50)
Рис. 294 Рис. 295 Рис. 296

2.2.32. На звено ВС шарнирного четырехзвенника (рис. 296) действует пара сил с моментом M₂ = 200 Н·м. Определить момент М₁ пары сил, который надо приложить к кривошипу ОА, для того чтобы механизм находился в равновесии, если длины звеньев ВС = 2 ОА = 400 мм. (100)

2.2.33. Шарнирный четырехзвенник (рис. 296), весом кото­рого можно пренебречь, находится в равнове­сии. Определить силу F, если к кривошипу ОА приложена пара сил с моментом М = 10 Н·м, а размеры ОА = 10 см, ВС = CD, угол α = 30°. (400)

2.2.34. На толкатель I кулачкового механизма (рис. 297) действует сила F = 100 Н. При каком моменте М пары сил, приложенных к кулачку 2, воз­можно равновесие механизма, если расстояние ОА = 10см. (7,07)

2.2.35. На призму 1 (рис. 298) действует сила F₁= 100 Н. Определить силу F₂, которую необходимо приложить к стержню 2, шарнирно связанному с роликом 3, для равновесия системы. (173)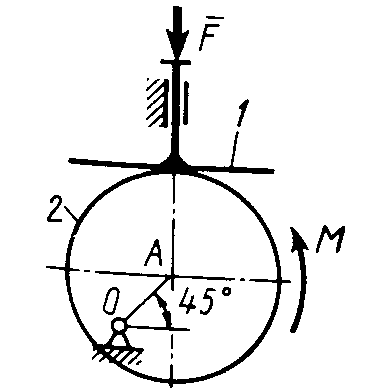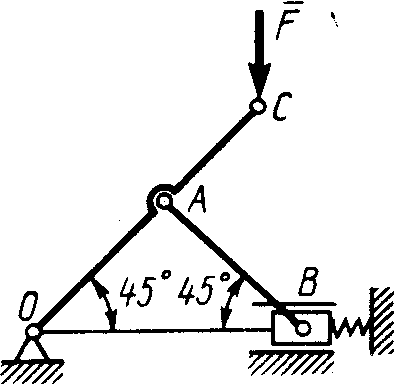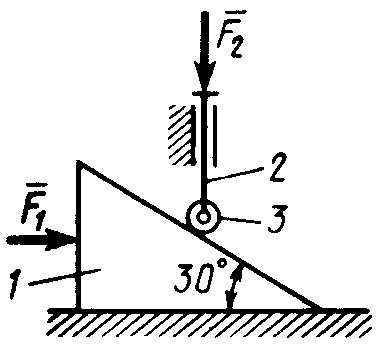




Рис. 297 Рис. 298 Рис. 299

2.2.36. Определить силу упругости пружины в кН при равновесии механизма (рис. 299), если сила взаимно­го давления кривошипа ОАС и шатуна АВ в шарнире А равна 1 кН. (0,707)

2.2.37. Кривошипно-ползунный механизм (рис. 300) нахо­дится в равновесии. Определить в кН силу взаимодействия кривошипа ОАС и шатуна АВ, если к точке С приложена вертикальная сила F₁ = 1 кН, размеры ОА = АС = 0,3 м, угол α =45°. (1,41)

2.2.38. Кулисный механизм (рис.301) находится в равновесии под действием сил F ₁= 1 кН и F₂. Опре­делить в кН силу давления втулки 1 на верти­кальный стержень 2, если углы φ = 30°, α = 60°, длины О = 0,5 м, ОД = 1,2 м. (2,08)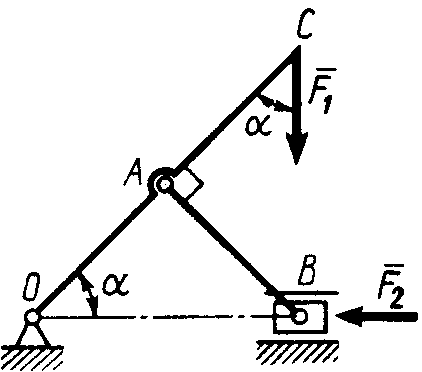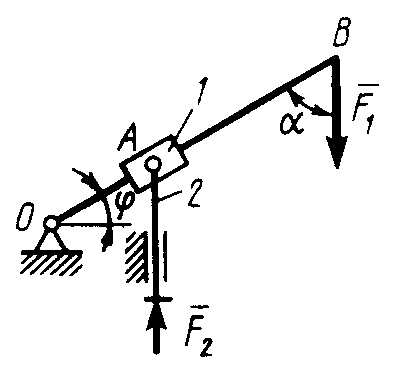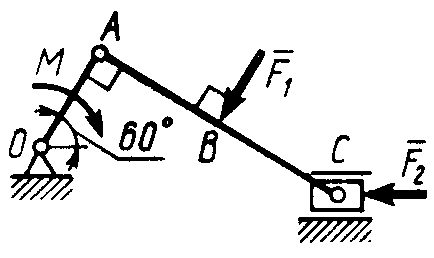



Рис. 300 Рис. 301 Рис. 302

2.2.38. Кривошипно-ползунный механизм (рис. 302) нахо­дится в состоянии равновесия под действием пары сил с моментом М, сил F₁ = 200 Н и F₂ = 500 Н. Определить силу воздействия поршня С на направляющую, если расстояния АВ = ВС = 30 см. (404)
2.3. ФЕРМЫ

2.3.1. Статически определимые и статически неопределимые фермы. Ненагруженные стержни

Фермой называется конструкция из стержней, соединенных между собой по концам шарнирно и образующих геометрически неизменяемую систему.

Фермой без лишних стержней называется такая ферма, в которой при удалении любого стержня нарушается ее геометрическая неизменяемость. Каждый стержень фермы испытывает только сжатие или растяжение, если выполняются следующие условия:

1. 
   Все стержни прямолинейные.
   
2. 
   Трение в шарнирах отсутствует.
   
3. 
   Заданные (активные) силы лежат в плоскости фермы (рассматриваем плоские фермы) и приложены только к узлам фермы.
   
4. 
   Весом каждого стержня можно пренебречь по сравнению с силами, приложенными к узлам фермы.
   
5. 
   Ферма без лишних стержней является фермой статически определимой. Это условие выражается формулой:
   

т = 2 п – 3,

где т – число стержней фермы, п – число узлов фермы.
Задачи

Статически определимые и статически неопределимые фермы

2.3.1. В скольких шарнирах нужно соединить 29 стержней, чтобы по­строенная с их помощью конструкция была плоской, статически определимой фермой? (16)

2.3.2. Которая из изображенных ферм является статически определимой? (2)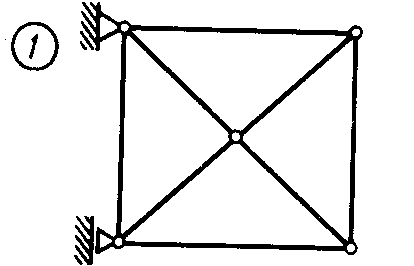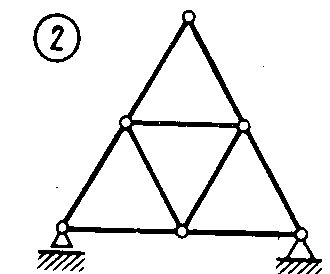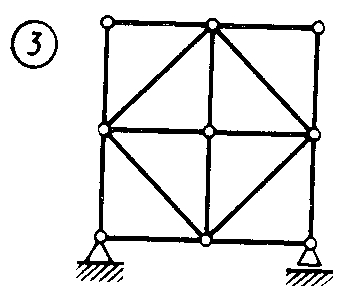




2 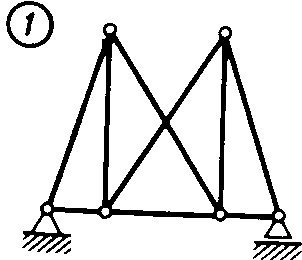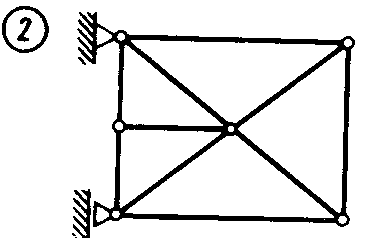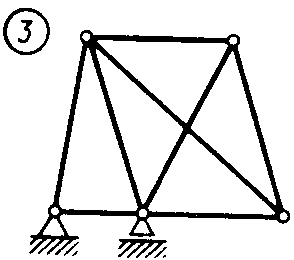.3.3. Которая из изображенных ферм является статически определимой? (1)

2.3.4. Которая из изображенных ферм является статически определимой? (3)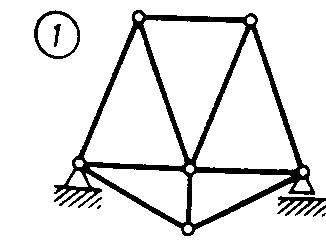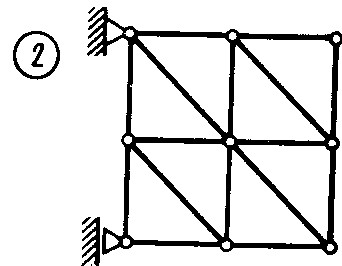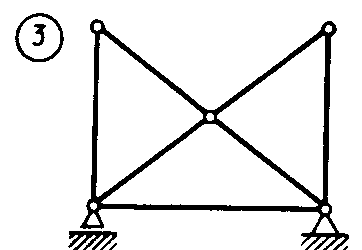




2.3.5. Которая из изображенных ферм является

с 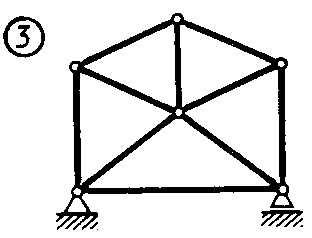татически неопределимой? (3)

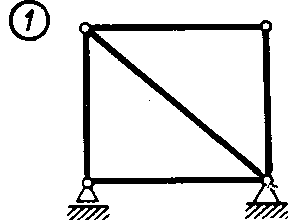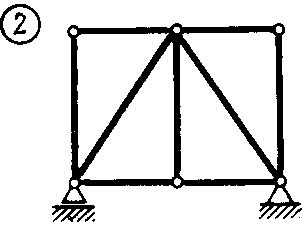2.3.6. Которая из изображенных ферм является статически неопределимой? (2)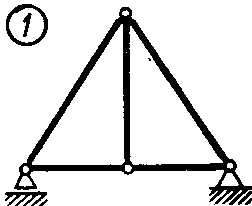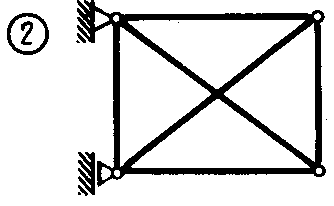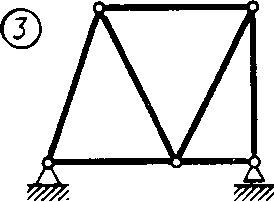




2.3.7. Который стержень фермы не нагружен? (5)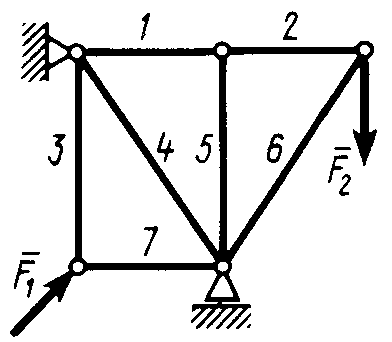

2.3.8. Который стержень фермы не нагружен? (7)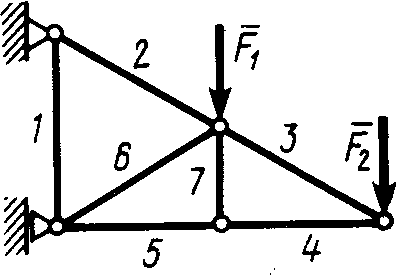



2.3.9. Который стержень фермы не нагружен? (5)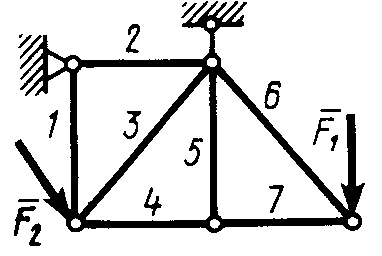

Способ вырезания узлов

2.3.10. Каким может быть максимальное число неизвестных реакций связей, приложенных к вырезаемому узлу плоской фермы, при определении усилий в стержнях фермы способом вырезания узлов? (2)

2 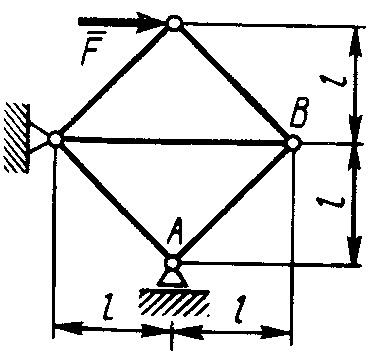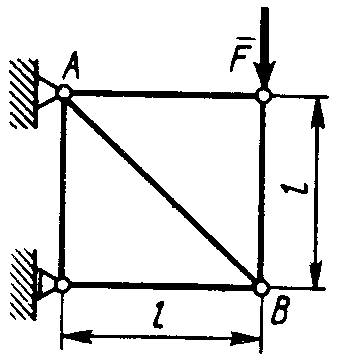.3.11. Определить усилие в стержне АВ (рис. 303). Сила F = 600 Н. (849)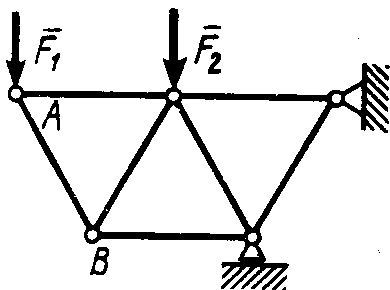



Рис. 303 Рис. 304 Рис. 305

2.3.12. Ферма состоит из стержней одинаковой длины (рис. 304). Определить усилие в стержне АВ. Силы F₁ = 100 H, F₂ = 200H. (-115)

2.3.13. Определить усилие в стержне АВ (рис. 305), если l = 0,4 м. Сила F=30 Н.

(-21,2)