Статика7. 2. статика в статике изучаются условия равновесия твердых тел под действием сил

• Название: 2. статика в статике изучаются условия равновесия твердых тел под действием сил
• Дата: 06.04.2021
• Размер: 1.32 Mb.
• Имя файла: Статика7.doc
• Тип: Документы; #191778
• страница: 9 из 9

Задачи

Центр тяжести линии

2.5.1. Определить координату х_С центра тяжести контура ABD(рис. 338), состоящего из однородных стер­жней АВ,AD и BD, имеющих одинаковый ли­нейный вес, если АВ = 2 м и угол α = 30°. (0,634)

2.5.2. Определить в см координату у_С центра тяжести однородной проволоки (рис. 339), состоящей из прямолинейного отрезка ОА и дуги АВ окруж­ности радиуса r = 20 см. (7,78)

2.5.3. Контур ОАВО состоит из прямолинейных отрезков ОА, ОВ и дуги АВ окружности ра­диуса r = 10 см (рис. 340). Определить в см² статический момент этого контура относительно оси Ох. (150)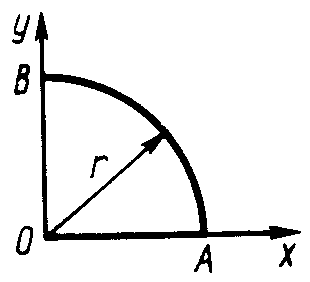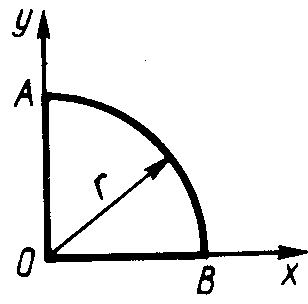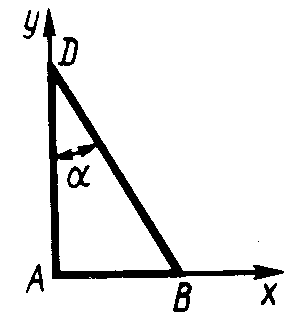




Рис. 338 Рис. 339 Рис. 340

2.5.4. Однородная проволока (рис. 341), согнутая в виде полуокружности, подвешена, как показано на рисунке. Определить угол α между вертикалью и диаметром полуокружности. (32,5)

2 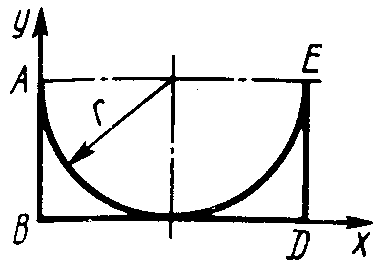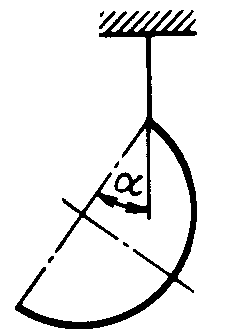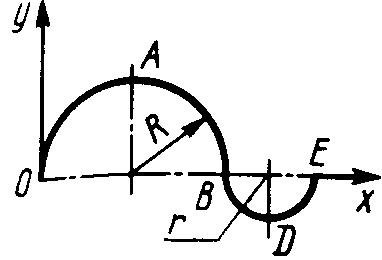.5.5. Контур состоит из двух однородных про­волок, согнутых в виде полуокружностей (рис. 342). Ли­нейный вес проволоки ОАВ равен 6 Н/м, а проволоки BDE - 10 Н/м. Определить коорди­нату х_Cцентра тяжести контура. (0,673)

Рис. 341 Рис. 342 Рис. 343

2.5.6. Определить координату у_C центра тяжести контура ABDEA(рис. 343), состоящего из прямолиней­ных отрезков АВ,BD,DE и полуокружности радиуса r = 1,2 м. (0,360)

2.5.7. Контур ОАВО состоит из прямолинейного отрезка ОА и полуокружности (рис. 344). Определить радиус r, если координата у_Cцентра тяжести этого контура равна 0,4 м. (1,03)

2.5.9. Определить координату х_C центра тяжести проволоки ABD (рис. 345), если даны следующие разме­ры: а = 1 м, b = 0,5 м, с = 0,8 м. (0,379)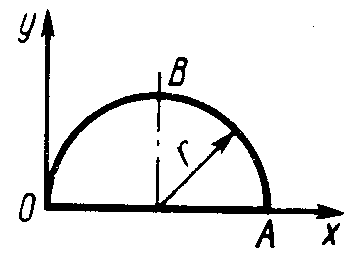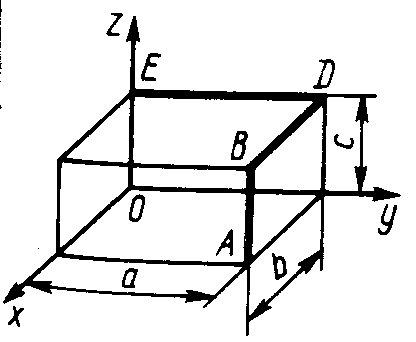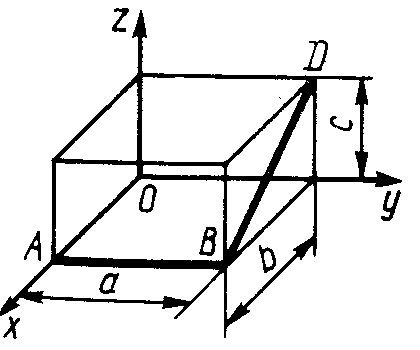



Рис. 344 Рис. 345 Рис. 346

2.5.10. Определить координату у_C центра тяжести проволоки ABDE(рис. 346), если даны следующие раз­меры: а = b= 2м, с = 1м. (1,60)

Центр тяжести плоских фигур

2.5.11. От пластины в виде прямо­угольного треугольника ОАВ (рис. 347) отсечен треугольник СDВ. Определить центр тяжести оставшейся части OADC, если СВ = а/3, ОА = ОВ = а. Ответ: х_С = 5а/18; у_С = 1За /3.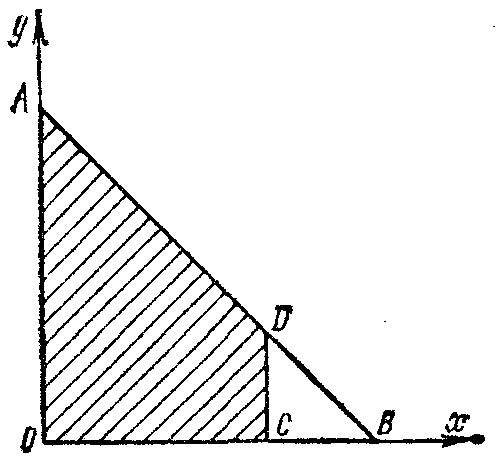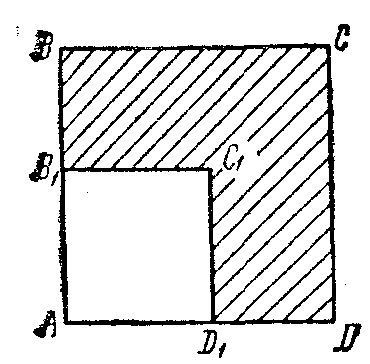






Рис. 347 Рис. 348

2.5.12. Из однородной пластины (рис. 348) в виде квадрата ABCD со стороной а вырезан квадрат AB₁C₁D₁так, что стороны обоих квадратов параллельны. Какова должна быть сторона а₁ меньшего квадрата для того, чтобы центр тяжести оставшейся после выреза части

совпал с точкой С₁? Ответ: .

2.5.13. Определить в см координату х_C центра тяжести однородной пластины, которая имеет вид прямоугольного треугольника ABD,если известны координаты вершин Х_A = Х_B = 3 см, X_D = 9 см. (5)

2.5.14. При каком расстоянии h от однородной пластины ABD (рис. 349) до оси Ох координата у_Cцентра тяжести пластины равна 0,3 м, если BD = 0,3 м. (0,2)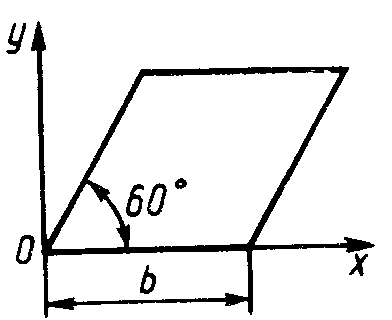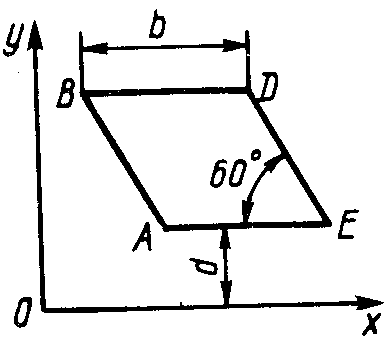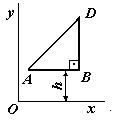




Рис. 349 Рис. 350 Рис. 351

2.5.15. Определить в см³ статический момент пло­щади ромба (рис. 350) относительно оси Ох, если сторо­на b = 8 см. (192)

2.5.16. Однородная пластина ABDE имеет вид ромба (рис. 351) со стороной b = 0,2 м. Определить ко­ординату у_C центра тяжести ромба, если рас­стояние d от основания АЕ до оси Ох равно 0,1 м. (0,187)

2.5.17. Определить координату у_Cцентра тяжести площади фигуры ABDEFG, стороны которой параллельны координатным осям (рис. 352). Размеры на рисунке заданы в м. (1,19)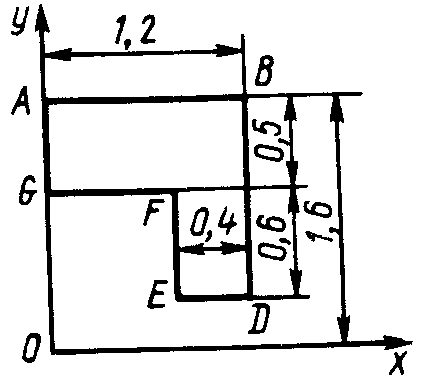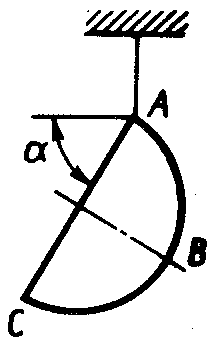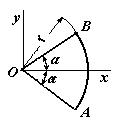




Рис. 352 Рис. 353 Рис. 354

2.5.18. Определить координату х_С центра тяжести площади кругового сектора ОАВ (рис. 353), если радиус r = 0,6 м, а угол α = 30°. (0,382)

2 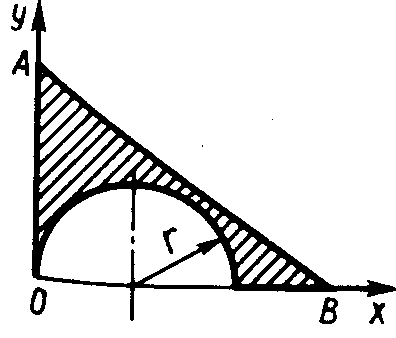.5.19. Однородная пластина АВС в виде полукру­га (рис. 354) подвешена за вершину А. Определить в гра­дусах угол α между горизонтальной осью и диаметром полукруга.( 67,0)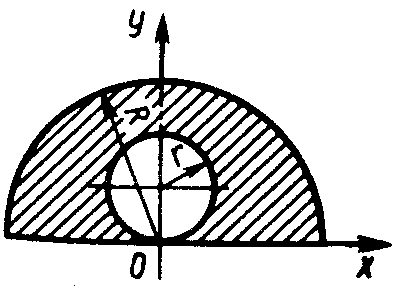



Рис. 355 Рис. 356

2.5.20. Определить координату центра тяжести у_Cзаштрихованной площади фигуры (рис. 355), если даны радиусы окружностей: R = 0,99 м, r = 0,33 м. (0,446)

2.5.21. Из однородной пластины в виде треуголь­ника ОАВ (рис. 356) с основанием OВ = 60 см и высотой ОА = 45 см вырезан полукруг радиуса r = 20 см. Определить в см координату x_Cоставшейся части треугольника. (20)

Центр тяжести тел

2.5.22*. Танкер водоизмещением 20 000 т в резуль­тате полученной подводной пробоины принял 600 т заборт­ной воды в танк (отсек) с координатами центра тяжести x₁ = 20 м, y₁ = 8м, z₁ = 2 м относительно координатных осей с началом в старом центре тяжести танкера. Для частичного выравнивания крена и дифферента (т. е. для устранения поворота судна вокруг продольной и поперечной осей) было принято дополнительно 400 т воды в танк с координатами центра тяжести х₂ = - 25 м, у₂ = 10 м, z₂ = 1 м. Определить новые координаты центра тяжести танкера.

Ответ: x_C = 9,5 см; у_C= 3,8 см; z_C = 7,6 см.

2.5.23*. Водоизмещение судна 1500 т. Определить новые координаты центра тяжести судна при заполнении носовой цистерны забортной водой плотностью ρ = 1,03 Н/м³, если объем цистерны V = 40 м³, а координаты центра тяже­сти цистерны х = 2 м, у = 30 м, z =1,5 м. До заполнения цистерны центр тяжести судна находился в начале коор­динат.

Ответ: х_С = 0,053 м; у_С = 0,8 м; z_C = 0,04 м.

2.5.24*. Как изменится абсцисса х_С общего центра тяжести корабля водоизмещением 1500 т, если поме­нять местами два груза, находящихся в диаметральной плоскости и отстоящих друг от друга по горизонтали на расстоянии s= 15 м? Массы грузов равны 10 и 2 т (ось Ох направлена на нос, более легкий груз был ближе к носу).

Ответ: Δх_С = 8 см (к носу).

2.5.25. Статический момент относительно плоско­сти Оху тела (рис. 357), состоящего из однородных ци­линдра и конуса, равен 0,166 м⁴ . Определить координату z_C центра тяжести тела, если ра­диус цилиндра r= 0,4 м и высота Н = 0,6 м. (0,413)

2.5.27. Тело состоит из однородного конуса 1 и однородного цилиндра 2 одинаковой высоты H(рис.358). Принимая удельные веса конуса и цилиндра соответственно равными γ₁ и γ₂. определить отношение γ₁/γ₂, при котором координата x_C центра тяжести тела равна нулю. (6)

2 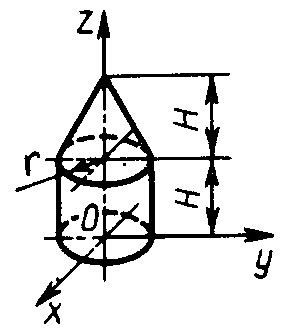.5.28. Определить высоту Н однородного прямо­угольного параллелепипеда (рис. 359) из условия, чтобы центр тяжести тела, состоящего из однородных призмы и параллелепипеда, находился в плос­кости ABCD. Высота призмы H₁ = 1,2. (0,490)

Рис. 357 Рис. 358 Рис. 359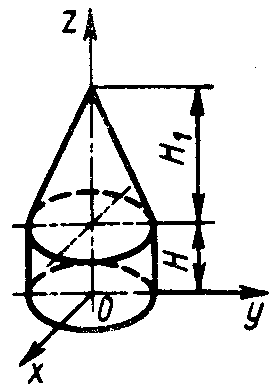

2 .5.29. Определить координату у_Cцентра тяже­сти однородного твердого тела (рис. 360), если даны сле­дующие размеры: r = 0,2 м, а = 0,5 м, b = 1,5м, с = 1,8м. (0,762)
Рис. 360 Рис. 361 Рис. 362

2.5.30. Определить высоту Н однородного цилин­дра (рис. 361), при которой ось симметрии тела, состоя­щего из двух цилиндров и подвешенного в точке А, будет горизонтальной. Высота ци­линдра H₁ = 0,5 м, радиус R = 3r. (1,5)

2.5.31. Определить координату z_C центра тяжести однородного тела (рис. 362), состоящего из конуса и цилиндра, если высота H₁ = 2H = 0,4. (0,18) 2.5.29. Определить координату z_C центр тяжести однородного тела (рис. 363), состоящего из прямоуголь­ного параллелепипеда и призмы, если высота

H₁= 3H = 1,2 м. (0,45)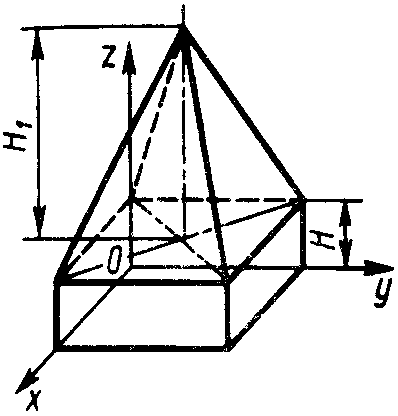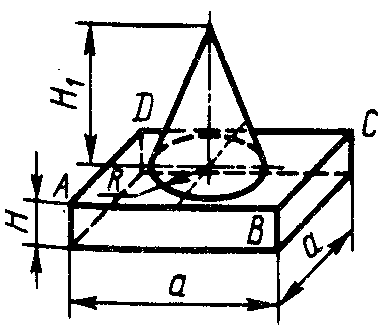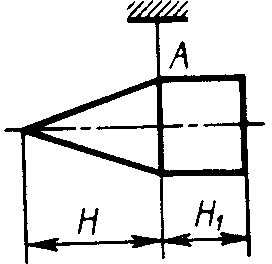




Рис. 363 Рис. 364 Рис. 365

2.5.32. Определить радиус R однородного конуса из

условия, чтобы центр тяжести однородного тела, состоящего из прямоугольного паралле­лепипеда и конуса, находился в плоскости ABCD(рис. 364). Высота H₁ = 3Н, размер а = 2 м. (0,92)

2.5.33. Определить высоту H однородного конуса (рис. 365), при которой ось симметрии тела, состоящего из конуса и однородного цилиндра и подве­шенного в точке А, будет горизонтальной. Высота H₁= 0,3 м. (0,735)