Произвольная система сил может быть в общем случае приведена к одной силе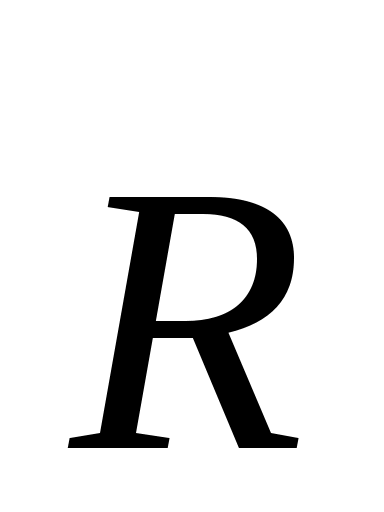 (главному вектору), равной сумме всех сил и приложенной в произвольном центре приведения О, и к одной паре, момент которой (главному вектору), равной сумме всех сил и приложенной в произвольном центре приведения О, и к одной паре, момент которой 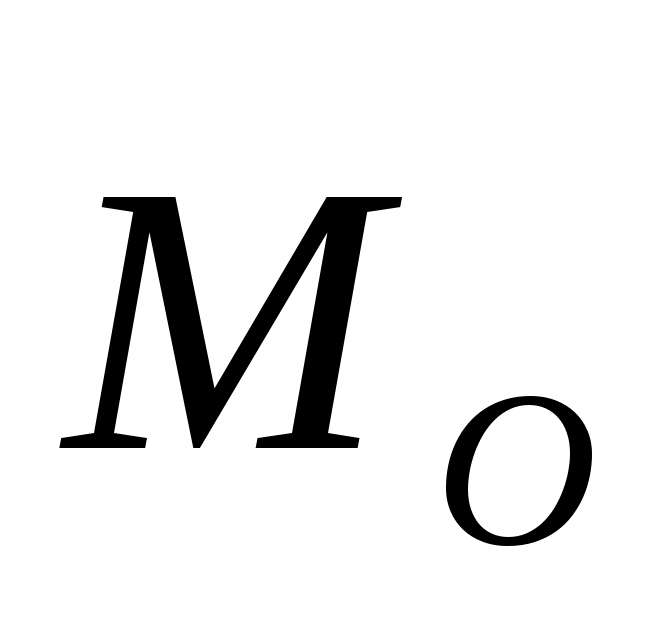 , называемый главным моментом, равен сумме моментов всех сил системы относительно этого центра: , называемый главным моментом, равен сумме моментов всех сил системы относительно этого центра:
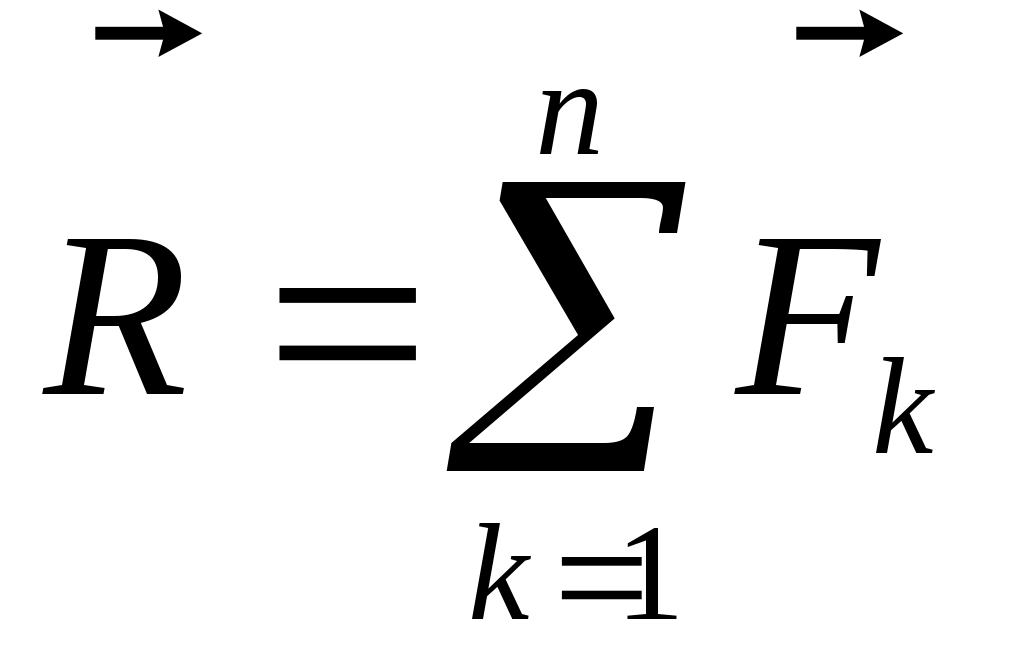 ; ; 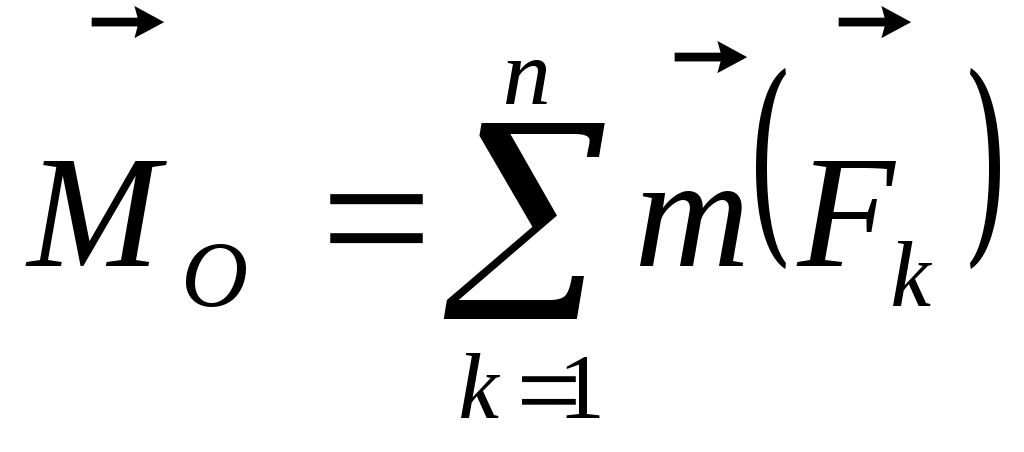 . (66) . (66)
При изменении центра приведения главный вектор сохраняет свой модуль и направление (первый инвариант), главный же момент изменяется, но так, что скалярное
произведение 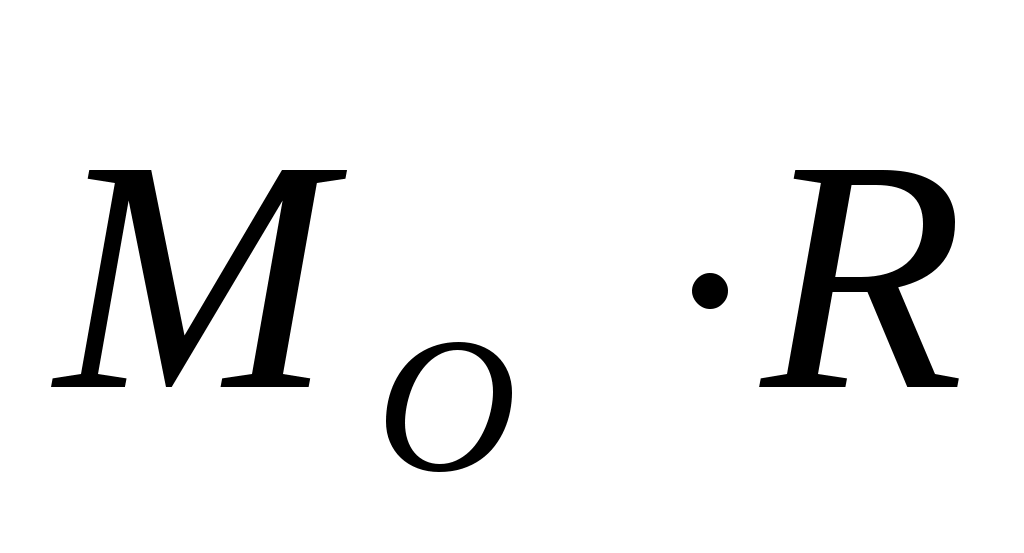 сохраняет одно и то же значение для всех точек приведения (второй инвариант). сохраняет одно и то же значение для всех точек приведения (второй инвариант).
Частные случаи;
1. Система приводится к равнодействующей, если 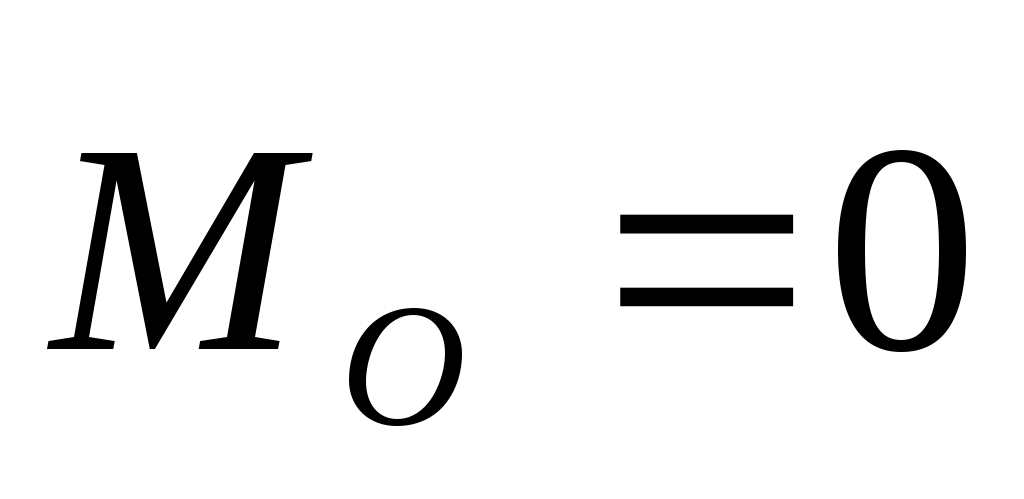 , , 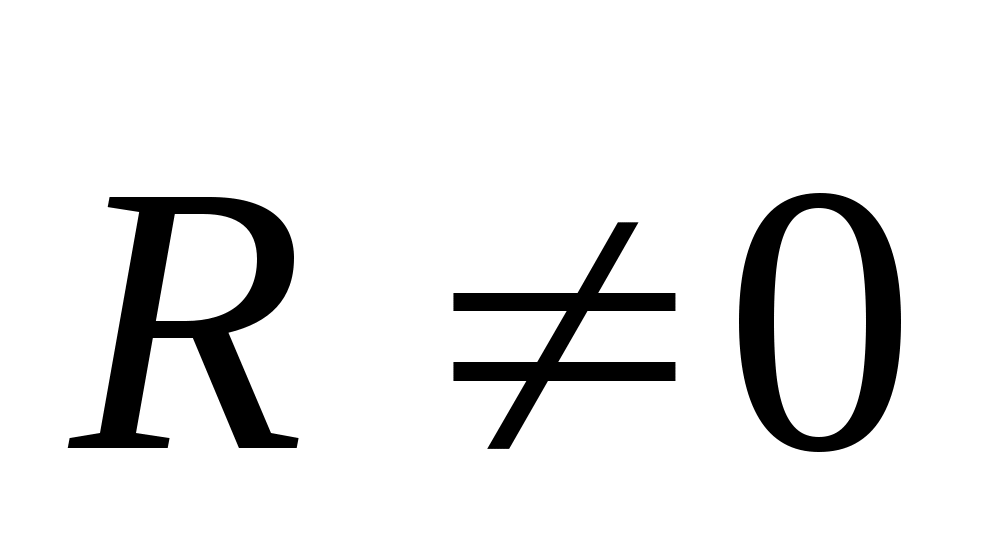 или или 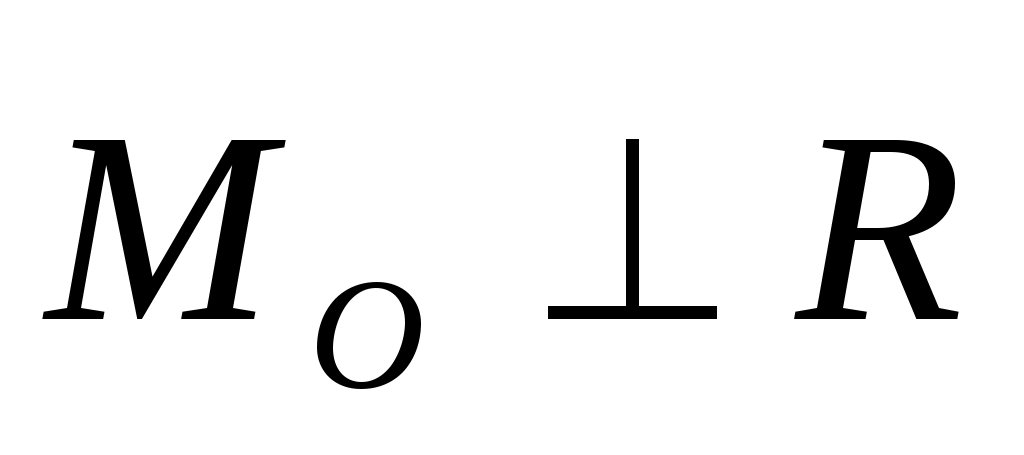
2. Система приводится к паре сил, если 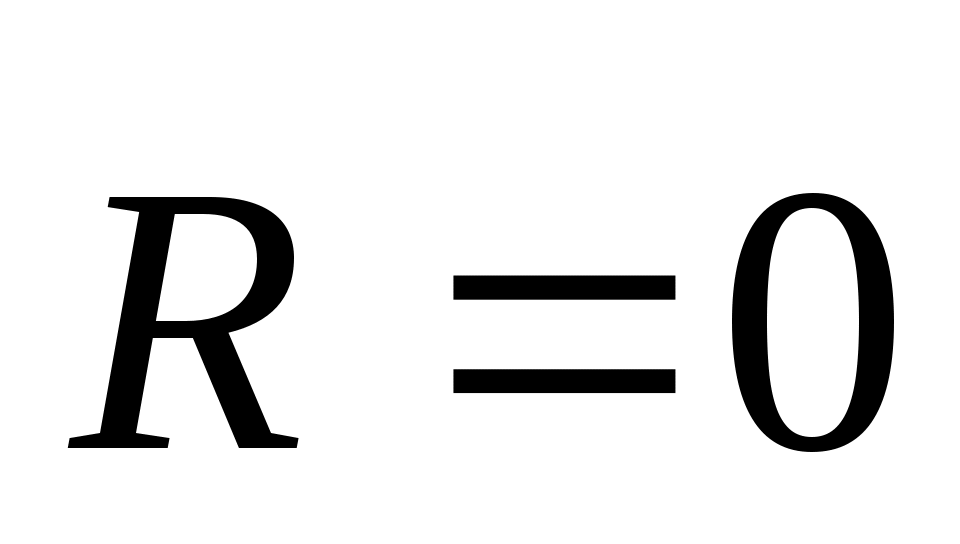 , ,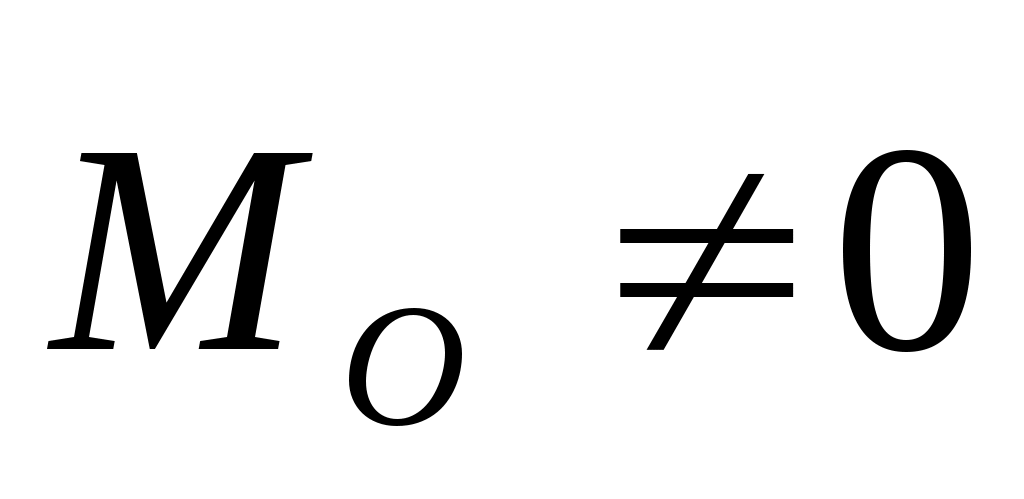
3. Система приводится к динамическому винту, если 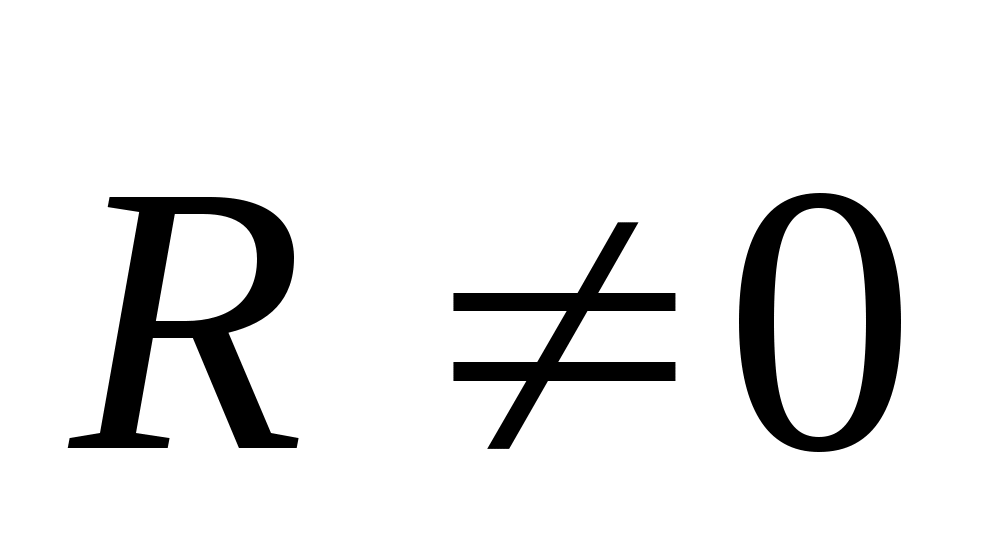 , ,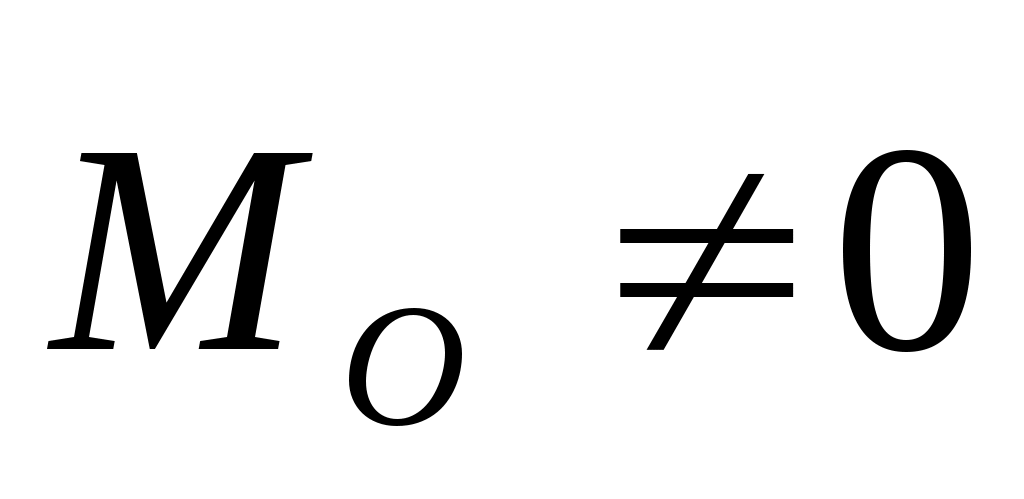 и эти векторы не перпендикулярны друг другу. При аналитическом задании сил ось динамы имеет уравнения и эти векторы не перпендикулярны друг другу. При аналитическом задании сил ось динамы имеет уравнения
: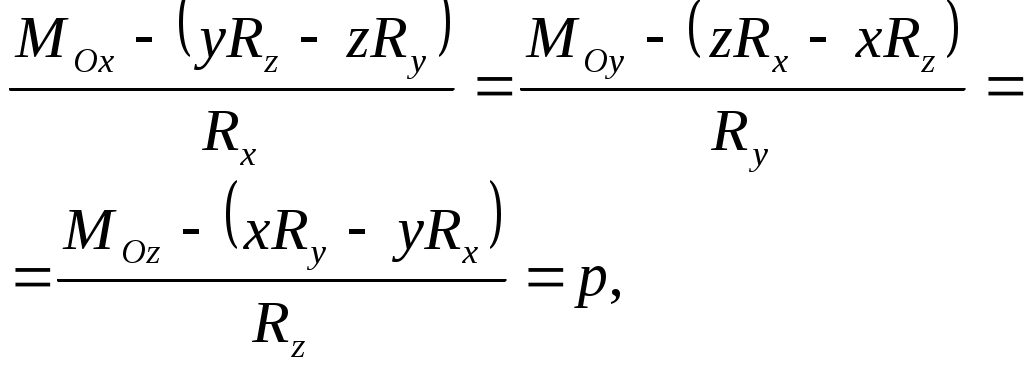 (67) (67)
где 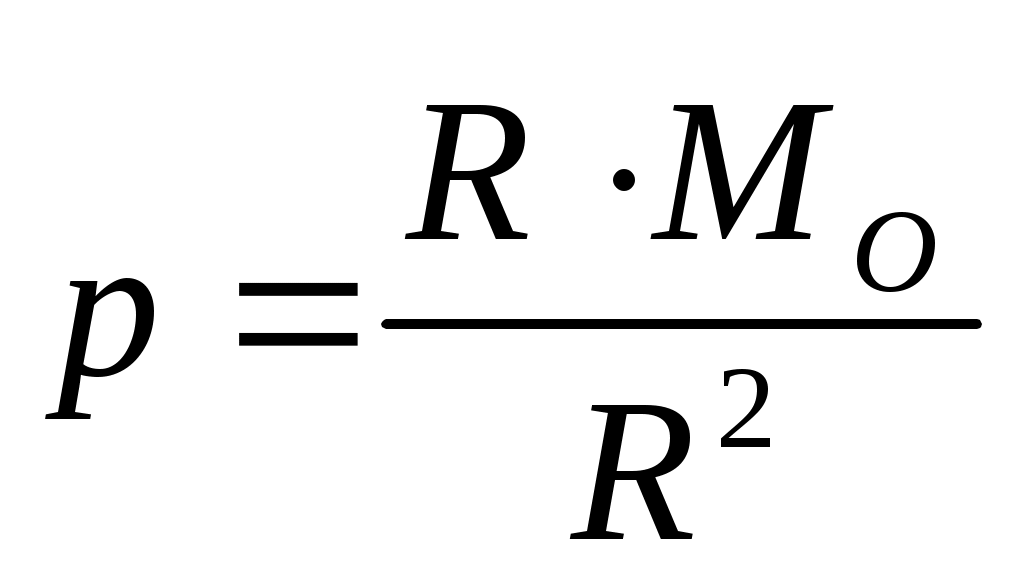 параметр динамического винта. параметр динамического винта.
4. Система находится в равновесии, если , 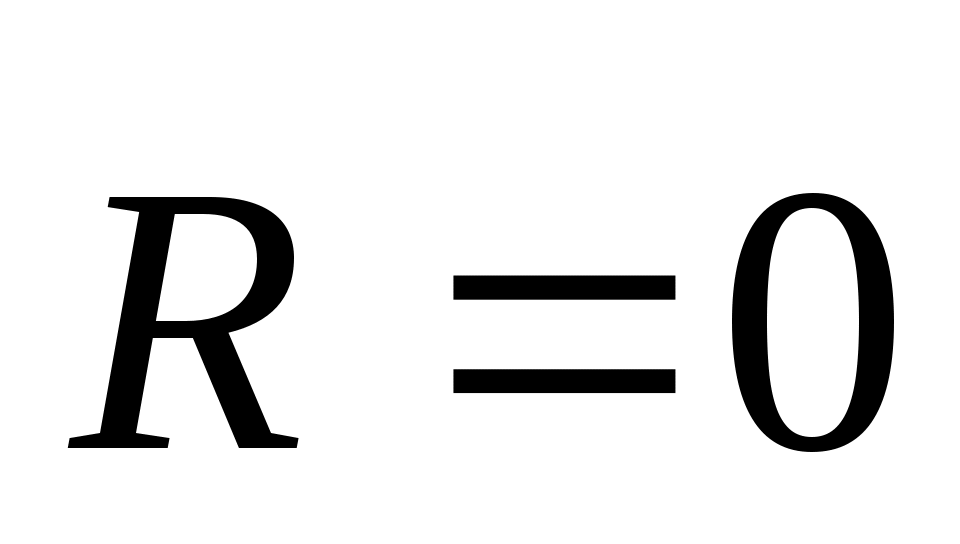 , ,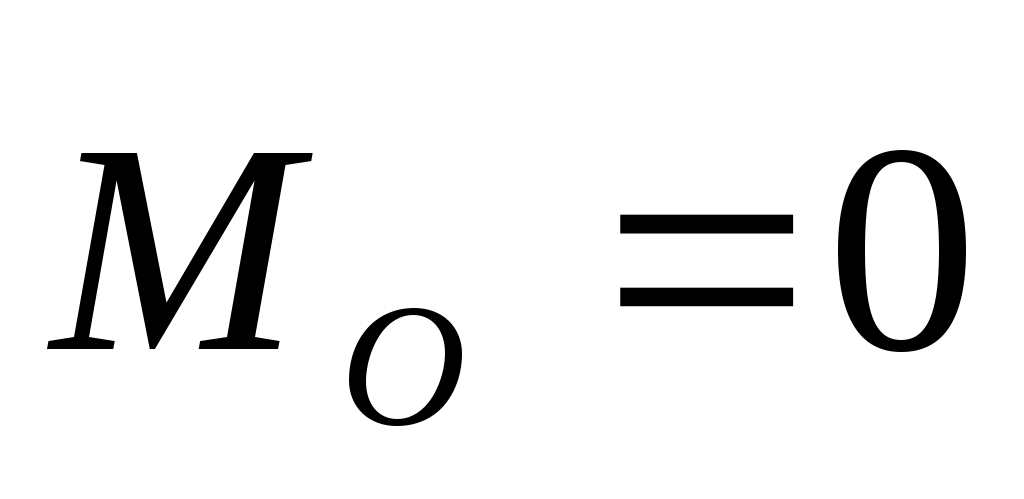 . Таким образом, для равновесия произвольной пространственной системы, сил необходимо и достаточно, чтобы для какого-либо центра приведения О главный вектор . Таким образом, для равновесия произвольной пространственной системы, сил необходимо и достаточно, чтобы для какого-либо центра приведения О главный вектор 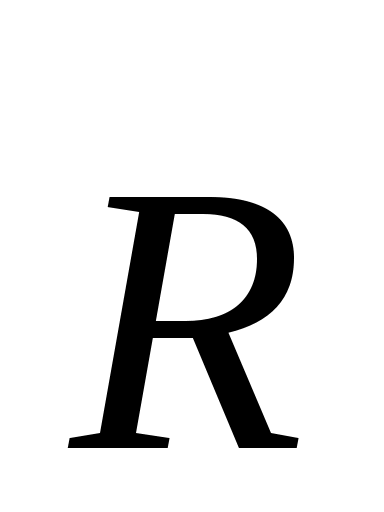 и главный момент и главный момент 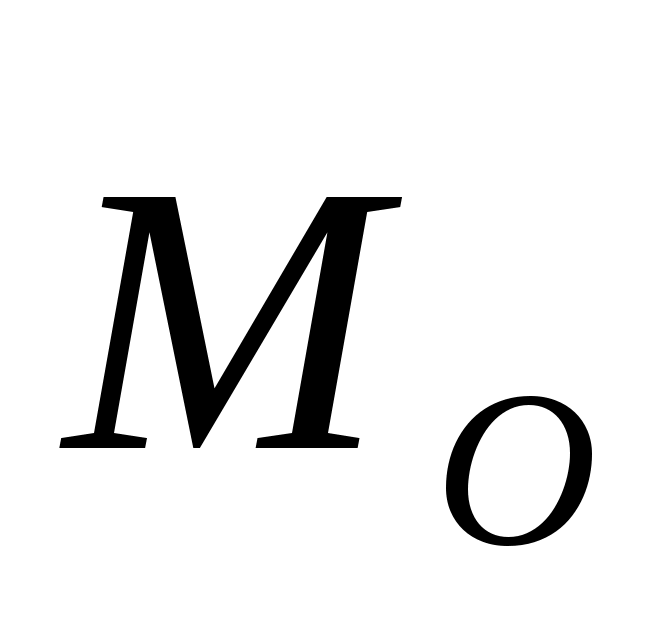 были равны нулю. были равны нулю.
Эти условия аналитически выражаются шестью уравнениями:
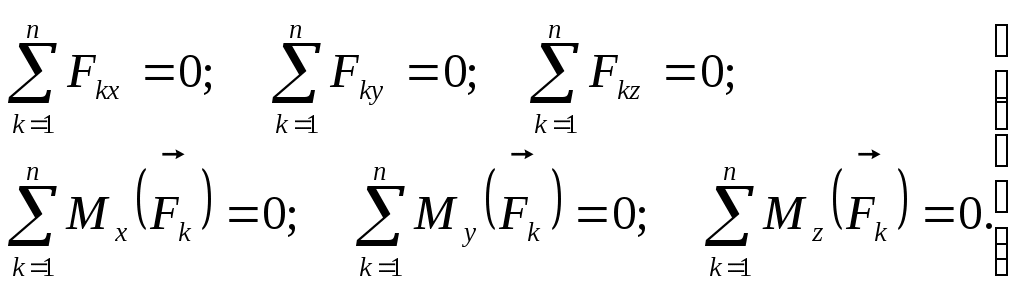 (68) (68)
Если на тело действует пространственная система параллельных сил, то, направив ось Оz параллельно этим силам, получим следующие три уравнения равновесия:
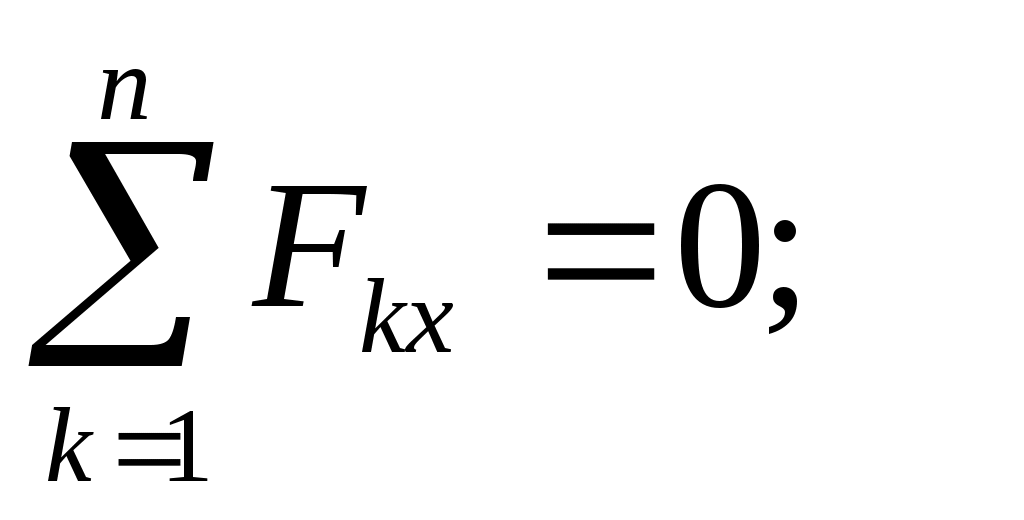 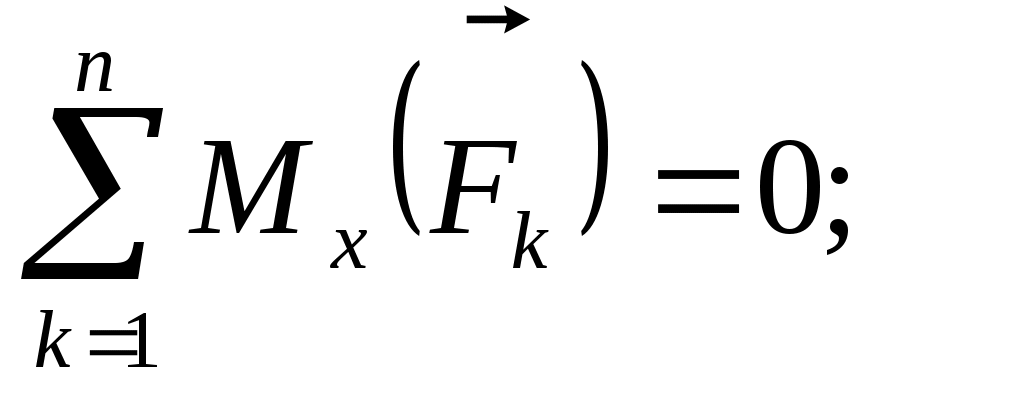 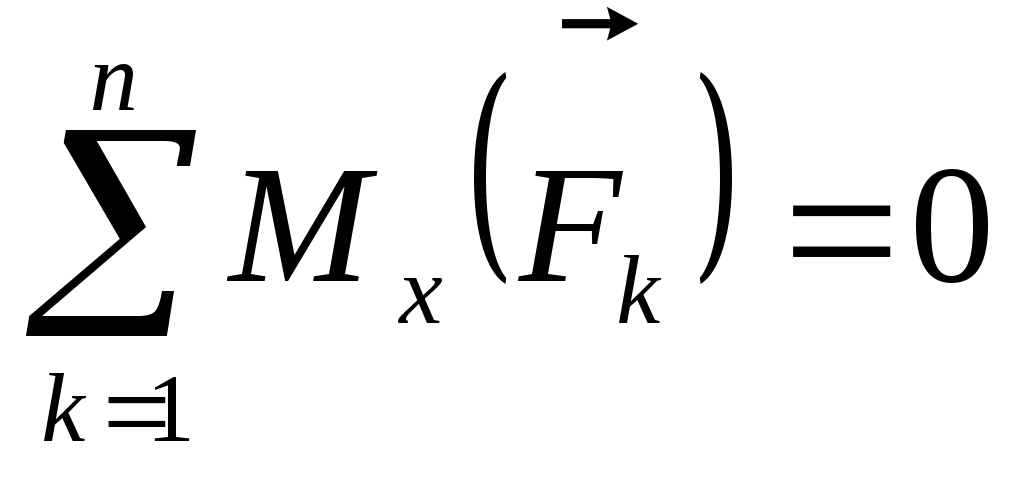 . (69) . (69)
Для нахождения момента силы относительно оси следует спроектировать силу на плоскость, перпендикулярную оси, после чего найти алгебраический момент полученной проекции относительно точки пересечения оси и проведенной плоскости. Момент силы относительно оси считается положительным, если при наблюдении с положительного конца оси кажется, что сила стремится повернуть тело против движения часовой стрелки.
Если сила параллельна оси или ее линия действия пересекает ось, то момент силы относительно оси равен нулю.
Значительно облегчает нахождение момента силы относительно оси применение теоремы Вариньона, согласно которой момент равнодействующей равен сумме моментов составляющих. Для применения этой теоремы силу, момент которой требуется определить, раскладывают на составляющие, одна из которых параллельна данной оси, а другие две перпендикулярны. Нахождение моментов этих составляющих обычно труда не представляет.
Если сила задана аналитически (т. е. заданы ее проекции и координаты точки приложения), то для определения моментов силы относительно координатных осей пользуются формулами
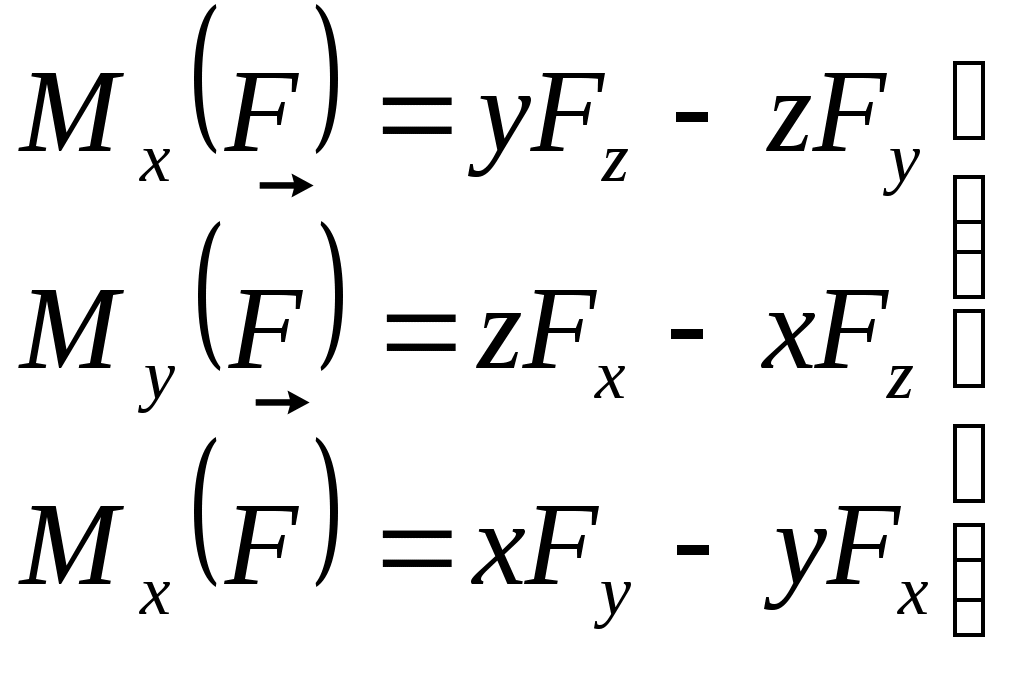 (70) (70)
где х, у, z - координаты точки приложения силы.
Рассмотрим теперь несколько примеров применения условий равновесия произвольной системы сил. При этом будем придерживаться следующей последовательности действий:
1) выяснить, равновесие какого тела будет рассматриваться в задаче и изобразить это тело на схеме;
2) построить на схеме все действующие на тело активные силы (как заданные, так и искомые);
3) определить виды связей, наложенных на рассматриваемое тело, мысленно отбросить их и заменить иx действие на тело соответствующими реакциями; построить эти реакции на схеме;
4) провести оси координат; желательно оси располагать так, чтобы они пересекали как можно больше неизвестных сил или были к ним перпендикулярны (если только это не усложнит вычисление проекций и моментов других сил);
5) определить вид полученной системы сил (включая активные силы и реакции), действующей на рассматриваемое тело, и составить соответствующие уравнения равновесия;
6) из полученных уравнений равновесия определить искомые величины и проанализировать полученные результаты.
В случае, когда из общей схемы трудно определить момент силы относительно оси, рекомендуется изобразить на вспомогательной схеме проекцию рассматриваемого тела (вместе с силой) на плоскость, перпендикулярную данной оси. Если же при вычислении момента силы относительно оси возникают затруднения в определении проекции силы на соответствующую плоскость или плеча этой проекции, то рекомендуется разложить силу на составляющие и воспользоваться теоремой Вариньона.
Пример 1. На горизонтальный вал, лежащий в подшипниках А и В, перпендикулярно оси вала насажены шкив D радиусом r2 = 30 см и барабан С радиусом r2 = 15 см (рис. 306). Вал приводится во вращение ремнем, накинутым на шкив; при этом равномерно поднимается груз М весом Р = 2500 Н. Трос, с помощью которою поднимается груз М, сходит с барабана по касательной, образующей с горизонтом угол 30°; ведомая ветвь ремня образует угол 30° с вертикалью. Пренебрегая весом конструкции, найти реакции подшипников А и В и натяжение Т1 ведущей ветви ремня, если Т1 = 2Т2. Необходимые размеры даны на рисунке
. Решение. Рассмотрим равновесие вала АВ со шкивом D и барабаном С. На это тело действуют активные силы натяжения ремней T1 и Т2, а также вес груза М. Последняя сила ( ) непосредственно к барабану не приложена; поэтому мысленно оборвав трос на его наклонном участке, заменим его действие на барабан реакцией. Так как силой трения в блоке Е можно пренебречь, реакция троса будет равна весу груза М. ) непосредственно к барабану не приложена; поэтому мысленно оборвав трос на его наклонном участке, заменим его действие на барабан реакцией. Так как силой трения в блоке Е можно пренебречь, реакция троса будет равна весу груза М.
Связями, наложенными на вал AВ, являются цилиндрические шарниры (подшипники) А и В. Поэтому реакция каждого из них имеет произвольное направление в плоскости, перпендикулярной оси вала. Проведя оси координат, как показано на рис. 306, а, представим каждую из этих реакций в виде их составляющих 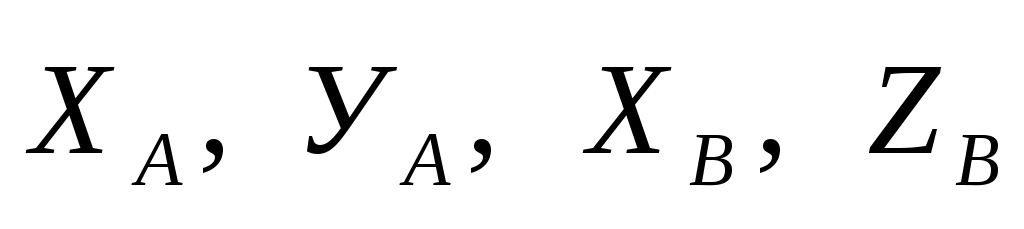 вдоль осей Ах и Az. Так как направление этих сил заранее неизвестно, направим их в сторону положительных направлений осей координат. Если в ответе величины данных составляющих реакций получатся положительными, то их выбранные направления соответствуют действительности, если же отрицательными, то в действительности они будут направлены в противоположном (по сравнению с рисунком) направлении. Число неизвестных в задаче равно пяти ( вдоль осей Ах и Az. Так как направление этих сил заранее неизвестно, направим их в сторону положительных направлений осей координат. Если в ответе величины данных составляющих реакций получатся положительными, то их выбранные направления соответствуют действительности, если же отрицательными, то в действительности они будут направлены в противоположном (по сравнению с рисунком) направлении. Число неизвестных в задаче равно пяти (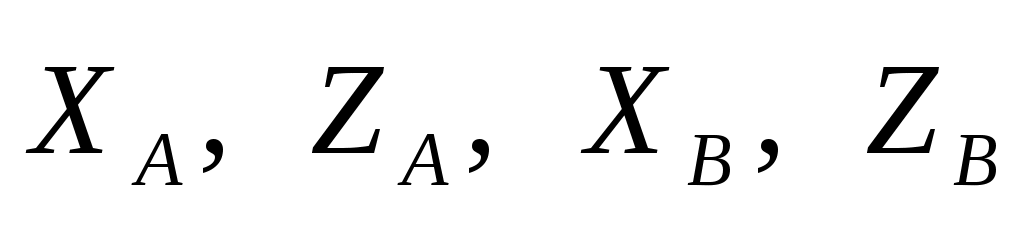 , , 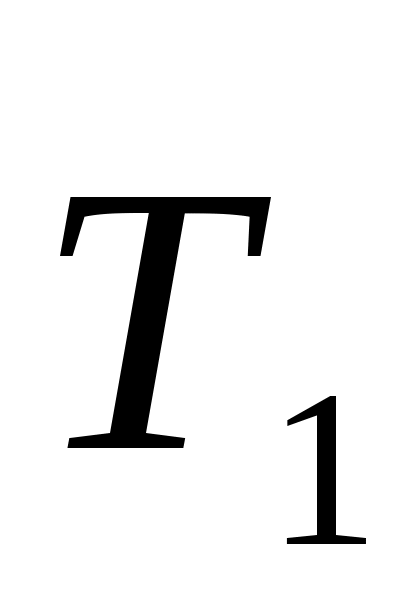 ) что не превышает числа уравнений равновесия; следовательно, задача является статически определимой ) что не превышает числа уравнений равновесия; следовательно, задача является статически определимой
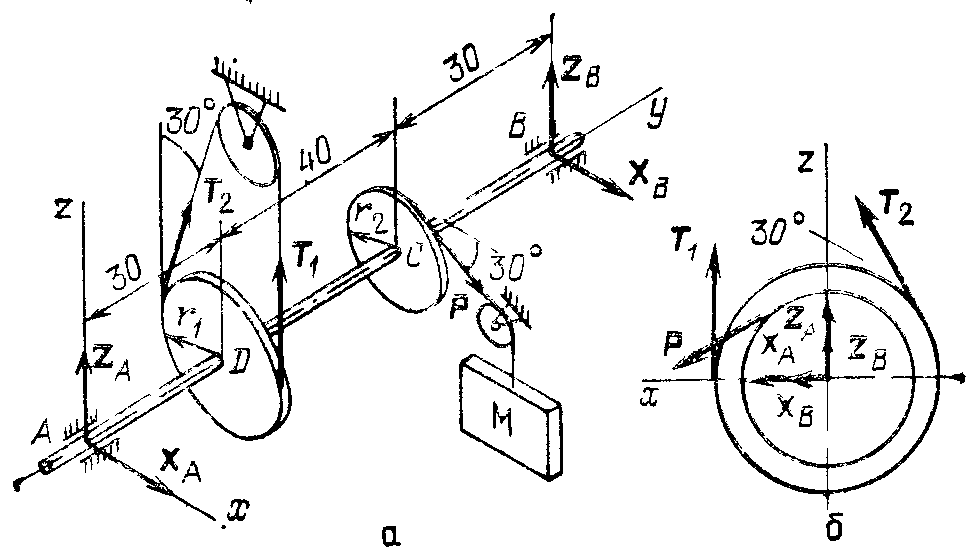
Рис. 306
Составим уравнения равновесия полученной произвольной системы сил {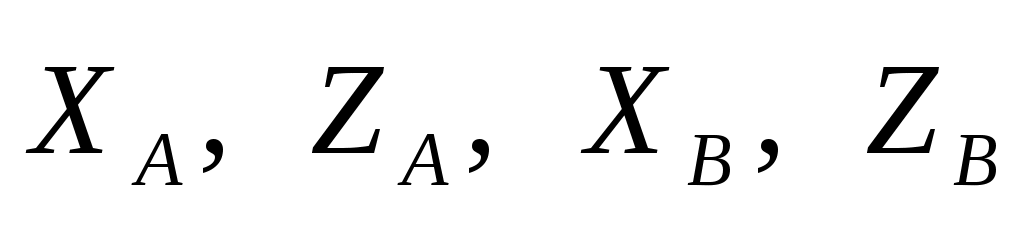 , , 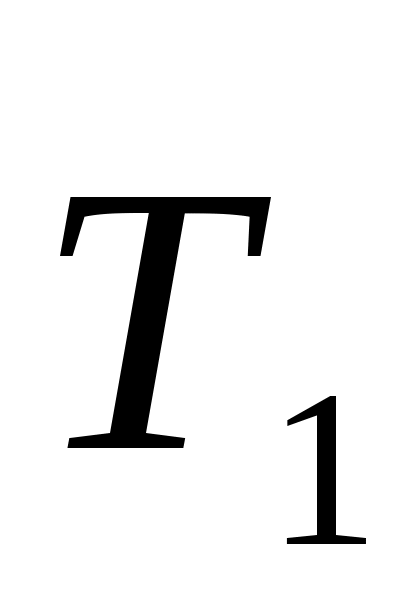 , , 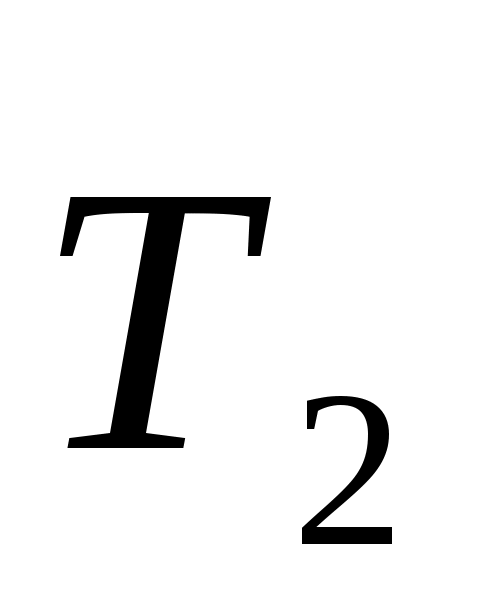 , , 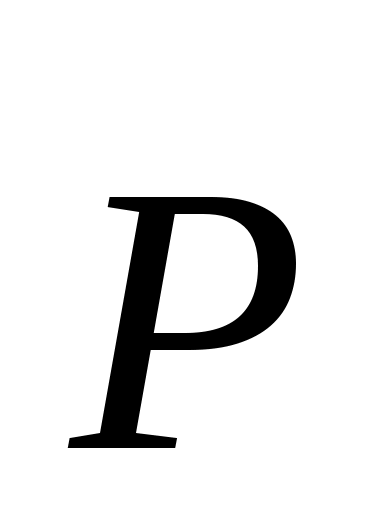 } ∞ 0. При определении проекций сил и их моментов воспользуемся видом на нашу конструкцию о положительного направления оси Ау (рис. 306, б) —такой вид полезен во всех тех случаях, когда рассматриваемое тело имеет ось вращения. Так как все силы перпендикулярны оси Ау, то на плоскость Axz они проектируются без искажения. } ∞ 0. При определении проекций сил и их моментов воспользуемся видом на нашу конструкцию о положительного направления оси Ау (рис. 306, б) —такой вид полезен во всех тех случаях, когда рассматриваемое тело имеет ось вращения. Так как все силы перпендикулярны оси Ау, то на плоскость Axz они проектируются без искажения.
Уравнения равновесия принимают вид
(1) 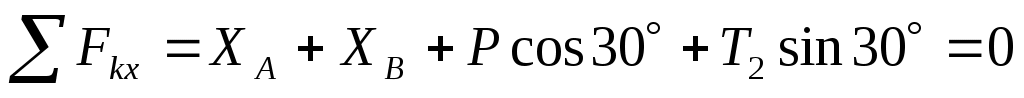 , ,
(2) 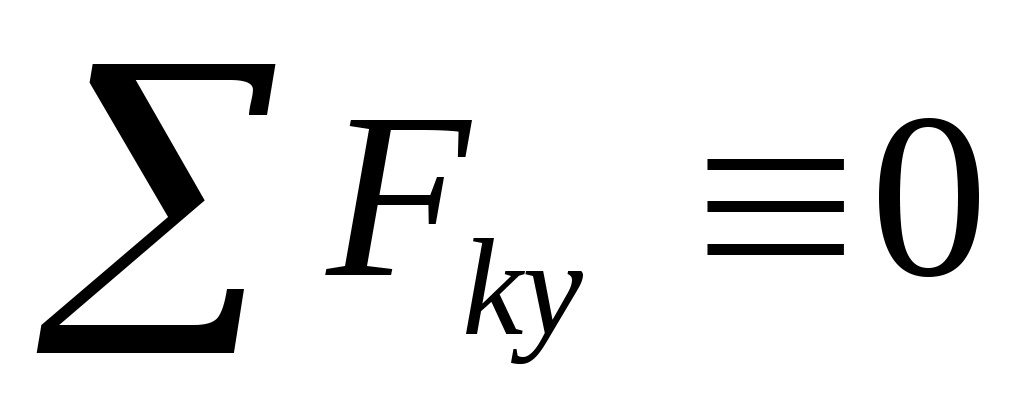 , ,
(3) 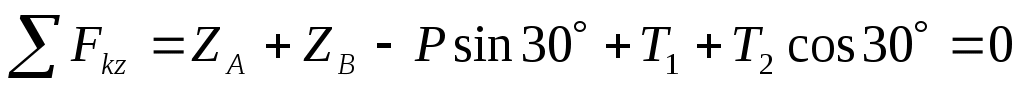 , ,
(4) 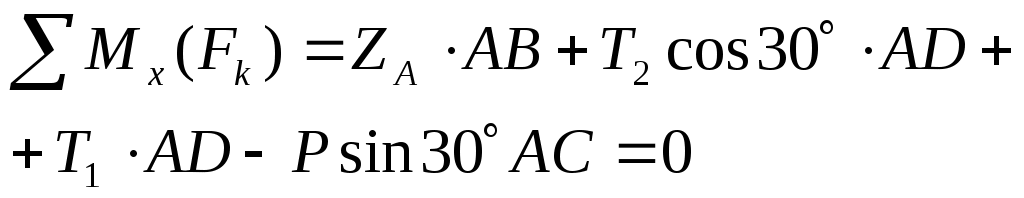 , ,
(5) 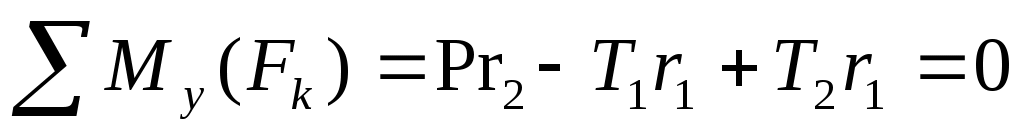 , ,
(6) 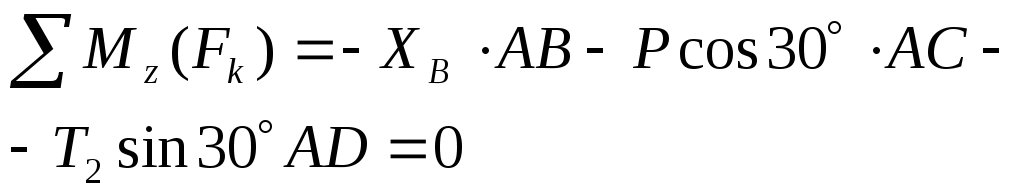 . .
Добавив к этим уравнениям равенство T1= 2Т2, получим систему шести уравнений с шестью неизвестными и решив ее, найдем из уравнения (5):
T2 = Pr2/r2 = 2500·15/30 = 1250 Н, Т1 = 2500 Н,
из уравнения (4): 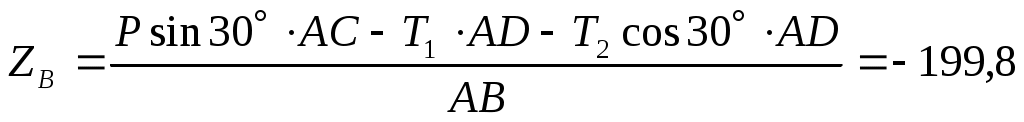 Н, Н,
из уравнения (6); 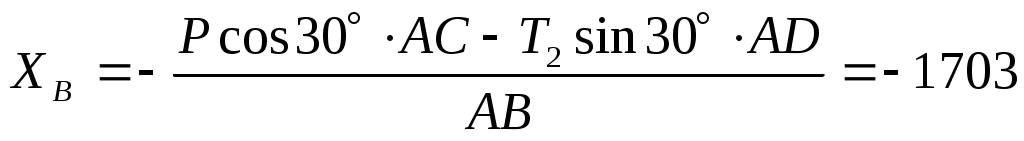 Н, Н,
из уравнения (1): ХА = ХВ – Рcos 30˚ - T2 sin 30˚= -1037 Н,
из уравнения (3): ZA = - ZB+ Р sin 30° - T1 - Т 2 cos 30° = -2133 Н.
Величины реакций 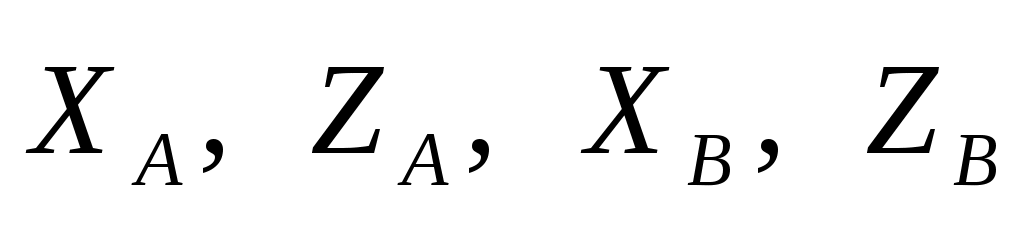 получились отрицательными. Это означает, что их направления в действительности противоположны указанным направлениям на рисунке. получились отрицательными. Это означает, что их направления в действительности противоположны указанным направлениям на рисунке.
Полные реакции шарниров А и В определятся по формулам
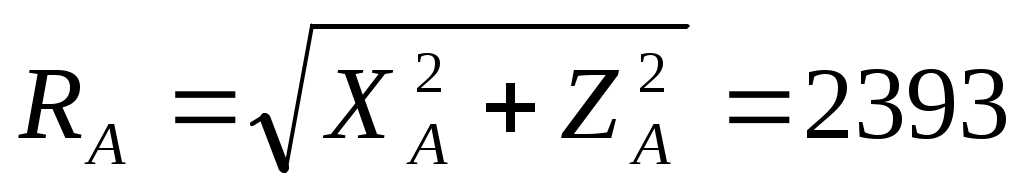 Н, Н, 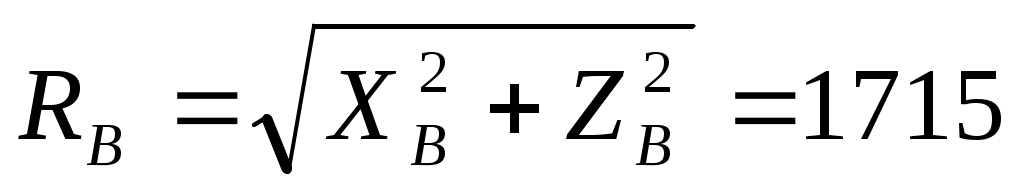 Н. Н. 
Пример 2. Однородная квадратная пластина ABCD весом Р = 120 Н (рис. 307) прикреплена к стене сферическим шарниром А и цилиндрическим шарниром В и удерживается в горизонтальном положении нитью CED, переброшенной в точке Е через гладкий гвоздь. Часть нити СЕ составляет с плоскостью пластины угол γ = 30°. Найти натяжение нити и реакции шарниров А и В.
Р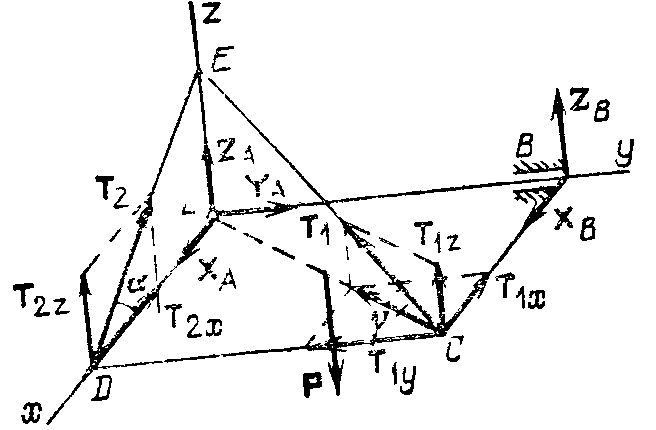 ешение. Рассмотрим равновесие пластины ABCD. На нее действует только одна активная сила ешение. Рассмотрим равновесие пластины ABCD. На нее действует только одна активная сила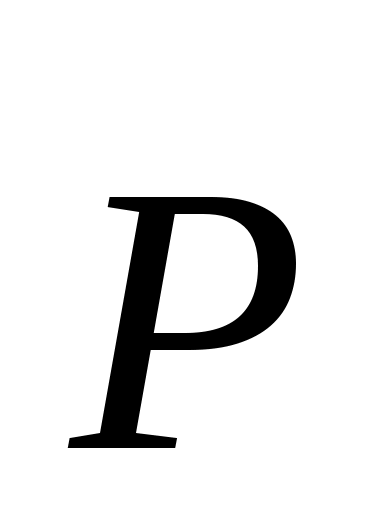 , приложенная в центре пластины. Связями являются сферический шарнир А с реакциями , приложенная в центре пластины. Связями являются сферический шарнир А с реакциями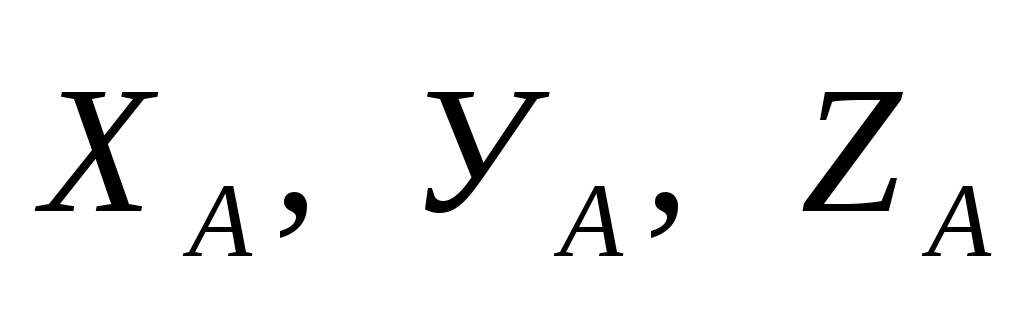 цилиндрический шарнир В с реакциями цилиндрический шарнир В с реакциями 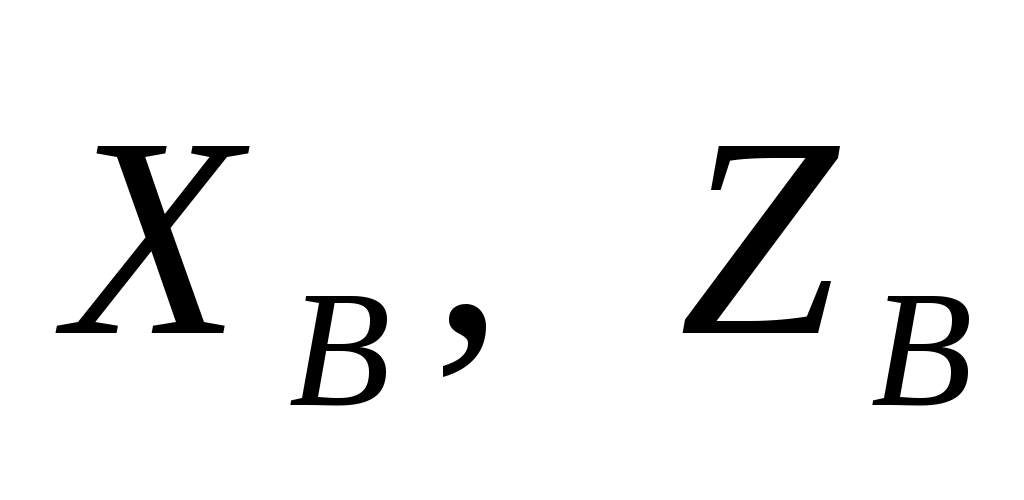 , а также нить DEC. Для того чтобы освободить пластину от действия нити, последнюю надо мысленно перерезать в двух местах, а именно на участке СЕ и на участке DE. , а также нить DEC. Для того чтобы освободить пластину от действия нити, последнюю надо мысленно перерезать в двух местах, а именно на участке СЕ и на участке DE.
Рис. 307 Поскольку гвоздь гладкий, натяжение нити в любом ее сечении постоянно, так что ее действие на пластину следует заменить двумя равными силами Т1 = Т2 = Т, приложенными в точках С и D.
Таким образом, освобожденная от связей пластина находится в равновесии под действием пространственной системы сил {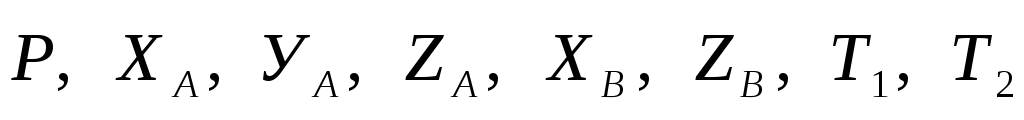 }∞0. Проведем оси координат, как показано на рисунке 307, и составим уравнения равновесия пластины. При этом, определяя проекции силы }∞0. Проведем оси координат, как показано на рисунке 307, и составим уравнения равновесия пластины. При этом, определяя проекции силы 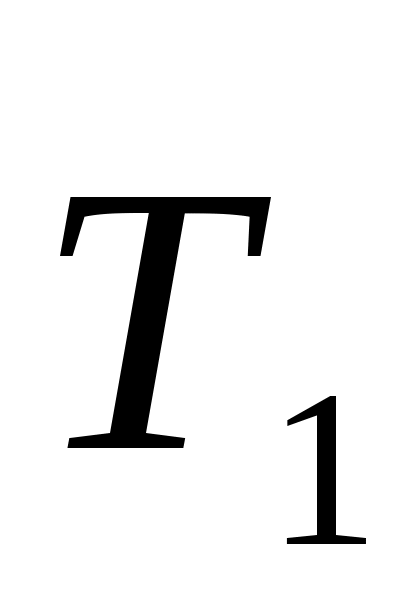 методом двойного проектирования, т. е. сначала найдем проекцию силы методом двойного проектирования, т. е. сначала найдем проекцию силы 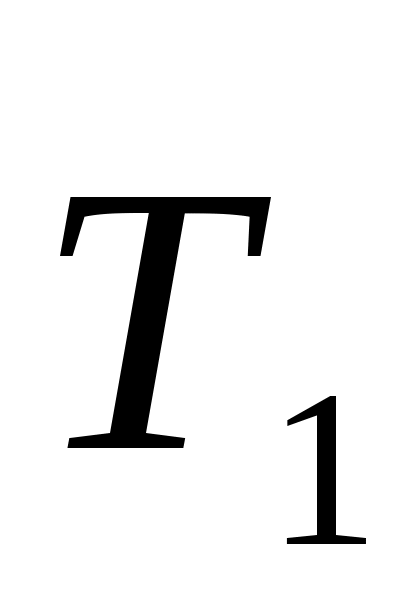 на плоскость Аху, а уже по ней найдем проекции на оси х и у: Т1ху =T1cos 30°, Т1х = Т1у = - Т1xу cos 45° = - T1 cos 30˚ cos 45°. на плоскость Аху, а уже по ней найдем проекции на оси х и у: Т1ху =T1cos 30°, Т1х = Т1у = - Т1xу cos 45° = - T1 cos 30˚ cos 45°.
Определяя моменты сил 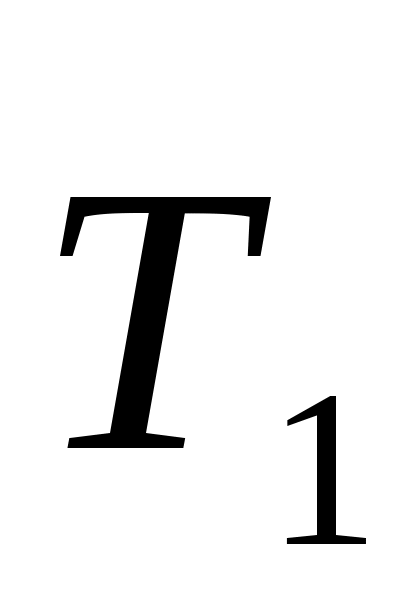 и и 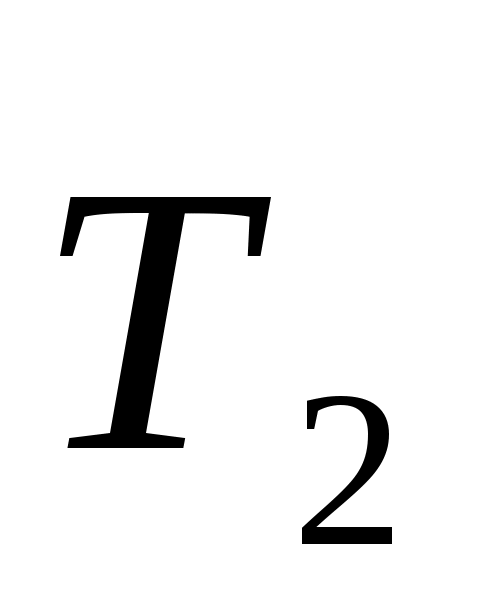 относительно осей координат, воспользуемся теоремой Вариньона. разложив cилy относительно осей координат, воспользуемся теоремой Вариньона. разложив cилy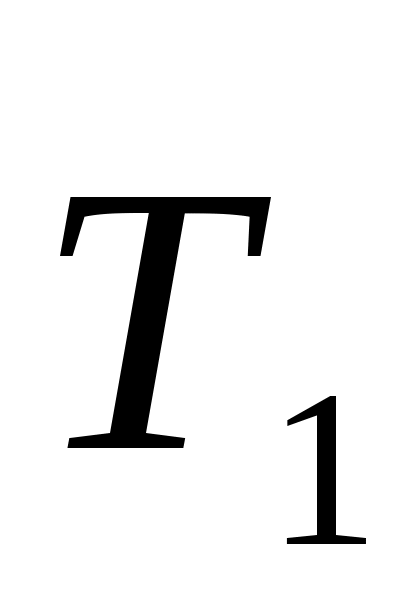 на составляющие на составляющие 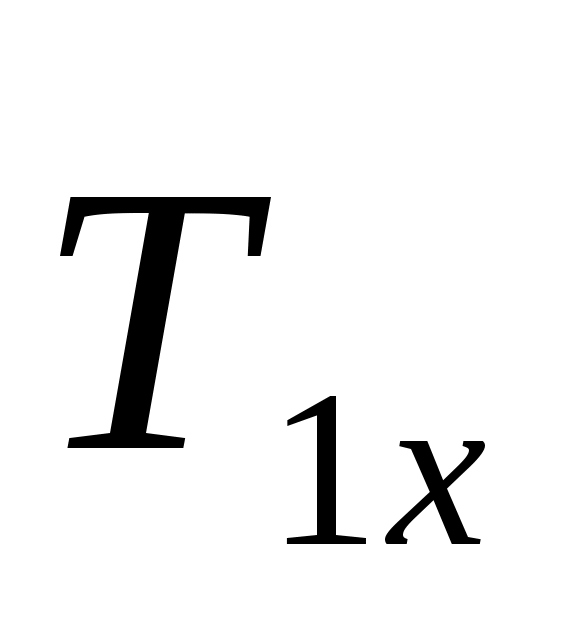 , ,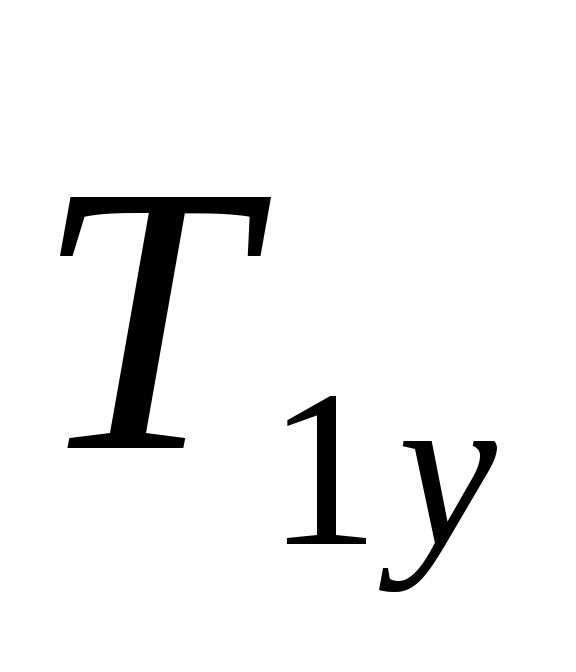 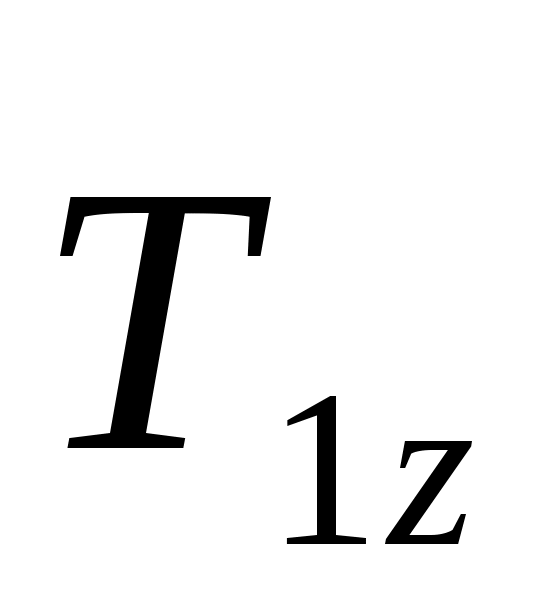 , а силу— , а силу—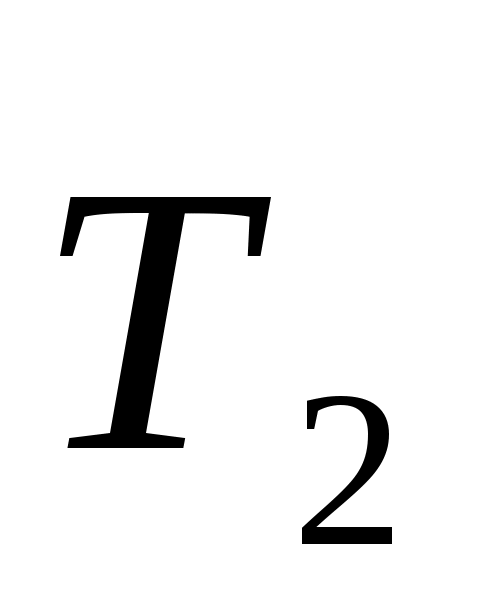 на составляющие на составляющие 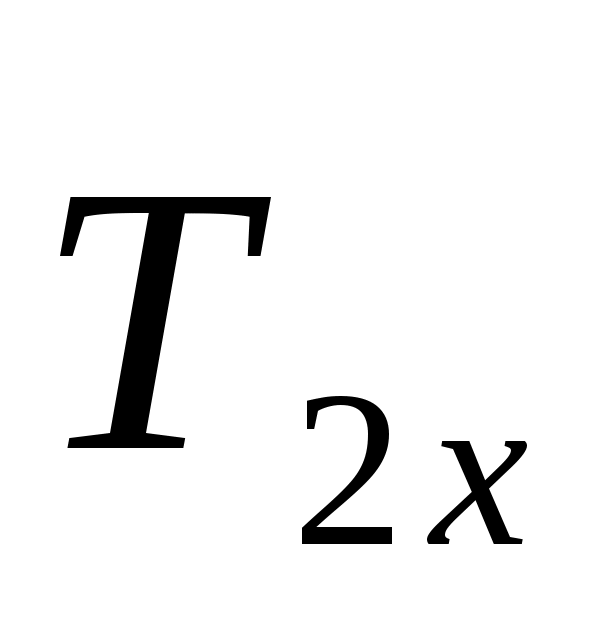 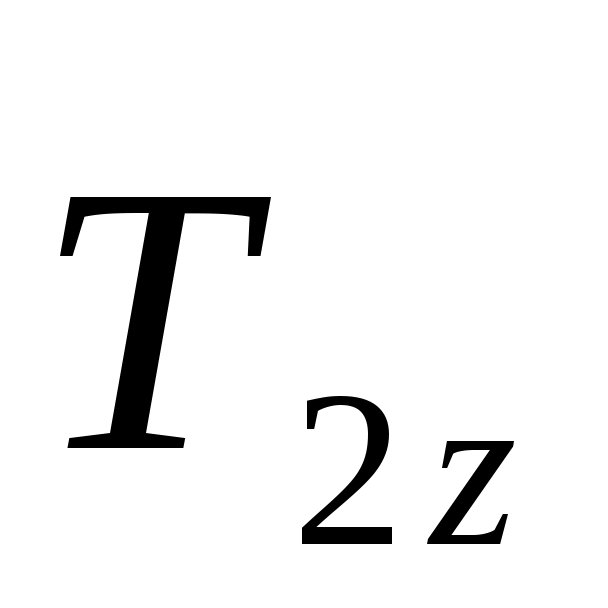 . Для определения величины Т2х и Т2z надо найти синус и косинус угла α, рассмотрев треугольники АЕС и AED:AC = AB√2, AE = AC tg 30° =АВ√6/3, . Для определения величины Т2х и Т2z надо найти синус и косинус угла α, рассмотрев треугольники АЕС и AED:AC = AB√2, AE = AC tg 30° =АВ√6/3, 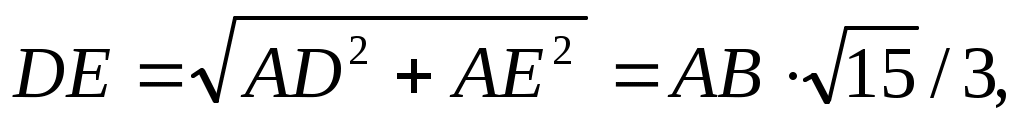 sin α= AE/DE = sin α= AE/DE =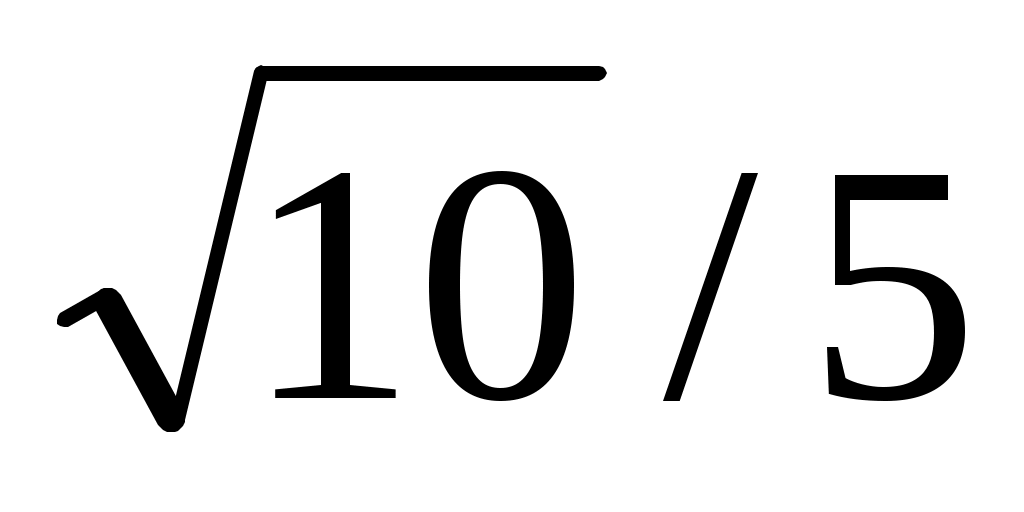 , , 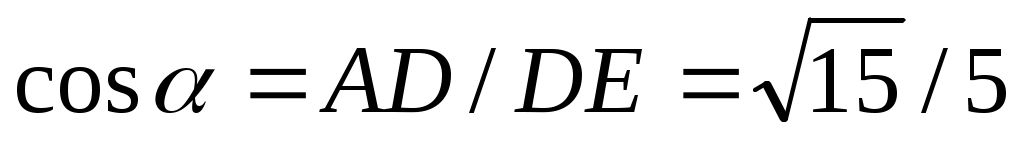 . .
Теперь составим уравнения равновесия:
(1) 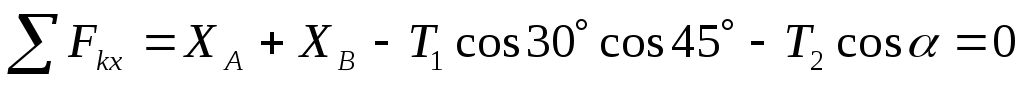 , ,
(2) 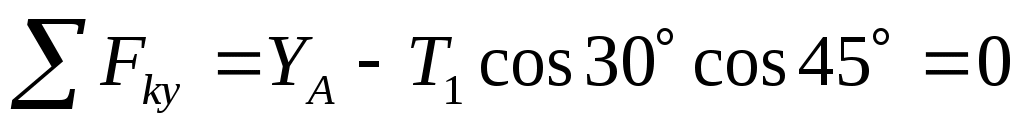 , ,
(3) 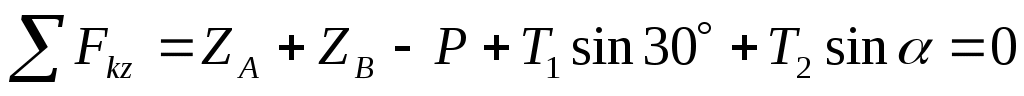 , ,
(4) 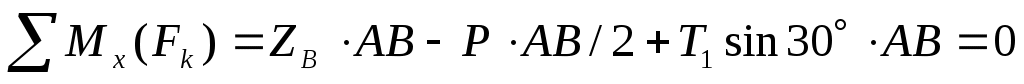 , ,
(5) 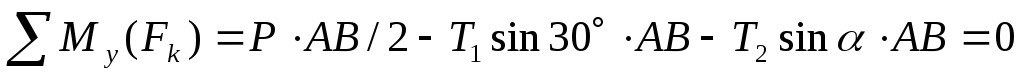 , ,
(6) 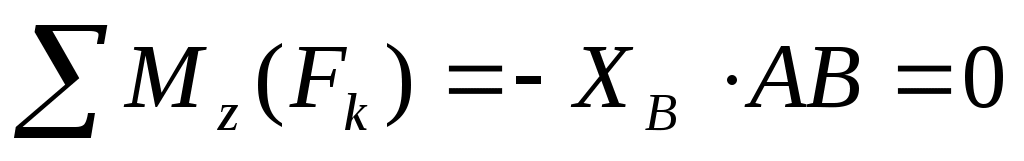 . .
Решив эту систему уравнении с учетом равенства Т1= Т2 = Т, получим
Т = 0,5Р/ (sin 30° + sin α) = 53 Н,
XA= T (cos 30° cos 45° + cos α) = 73,1 Н,
ХB = 0,
Yа= T cos 30° cos 45° = 32,6 Н,
ZB = - T sin 30° + 0,5P = 33,5 H,
Za = - Zb - T (sin 30° + sin α) + Р = 26,5 Н.
Найденные значения неизвестных положительны, поэтому направления реакций, показанные на риc. 307, соответствуют действительности. Как правило, при определении реакции ограничиваются нахождением лишь их составляющих, что мы и будем делать в дальнейшем.
Пример 3. На прямоугольный параллелепипед (рис. 308) действуют силы 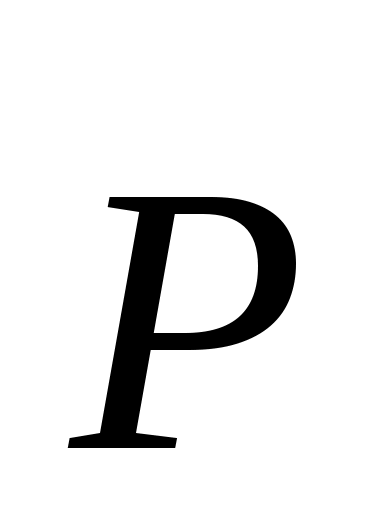 и и 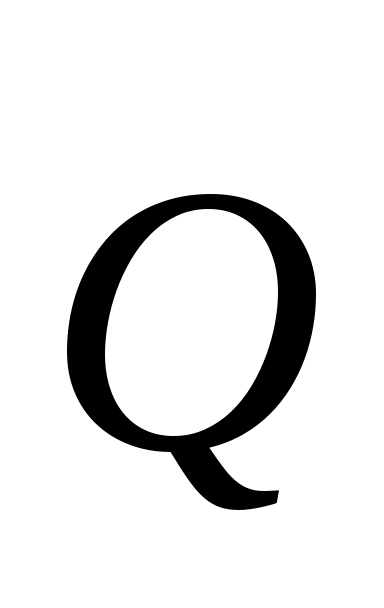 . Определить моменты этих сил относительно координатных осей, если ОA = 3 см, ОС = 4 см, . Определить моменты этих сил относительно координатных осей, если ОA = 3 см, ОС = 4 см,
OL = 5 см, а модули сил равны 3 Н.
Р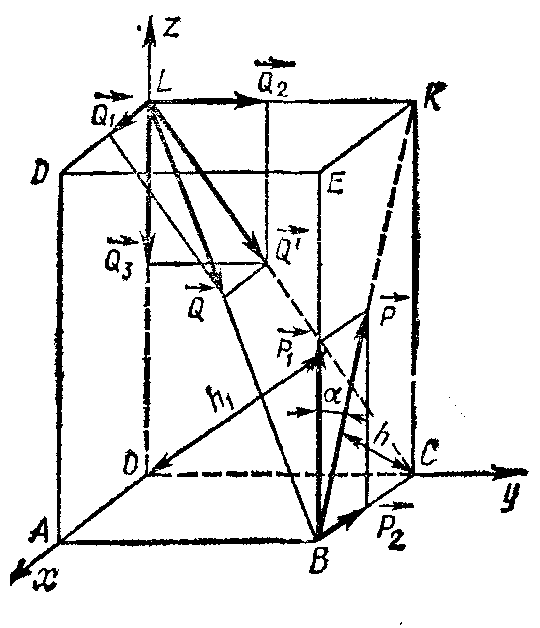 ешение. Найдем ешение. Найдем 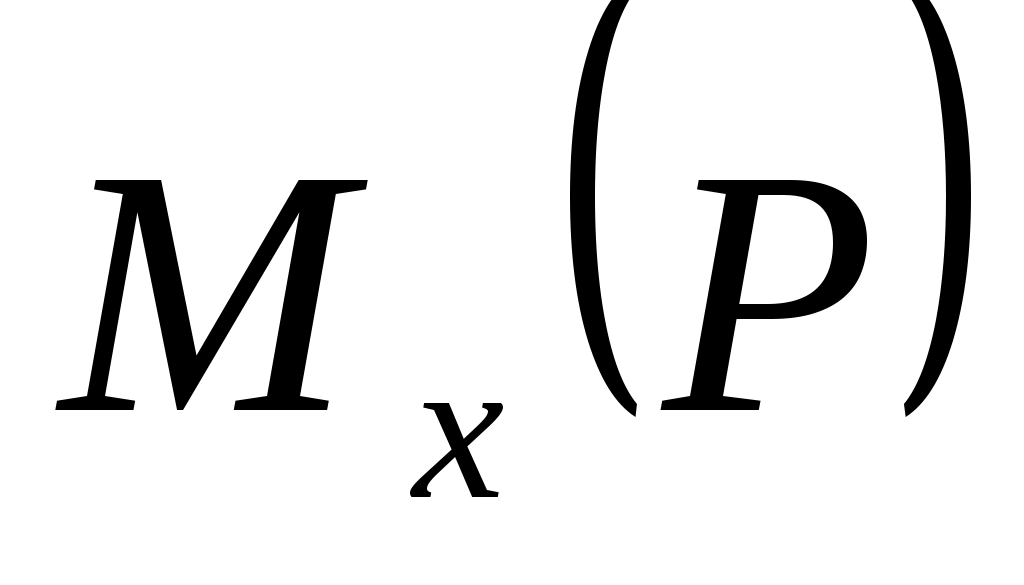 пользуясь опре-делением момента силы относительно оси. Для этого проектируем вектор пользуясь опре-делением момента силы относительно оси. Для этого проектируем вектор 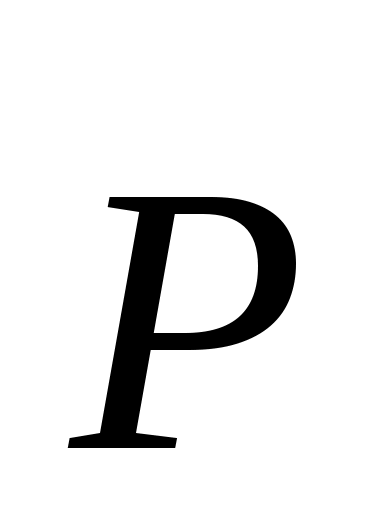 на плоскость ABED, перпендикуляр-ную оси Ох.Полученная проекция на плоскость ABED, перпендикуляр-ную оси Ох.Полученная проекция 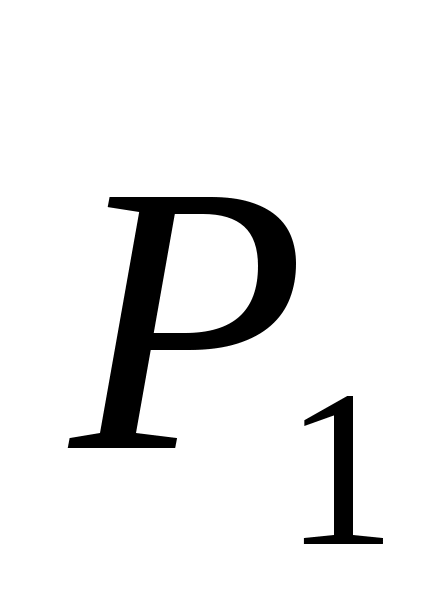 будет направлена по BE и равна по модулю будет направлена по BE и равна по модулю
P1= Р cos α.
Учитывая, что
сos α = ВЕ/ВК =5 /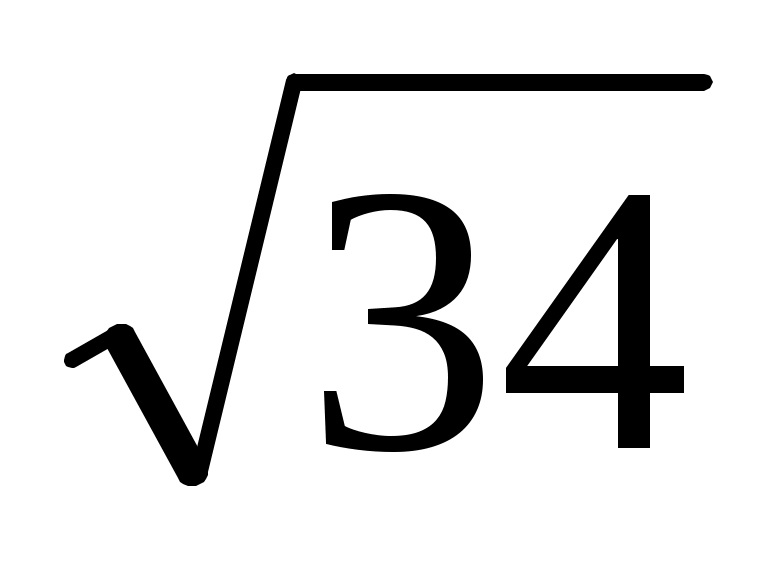 , ,
Рис. 308 получим P1=15/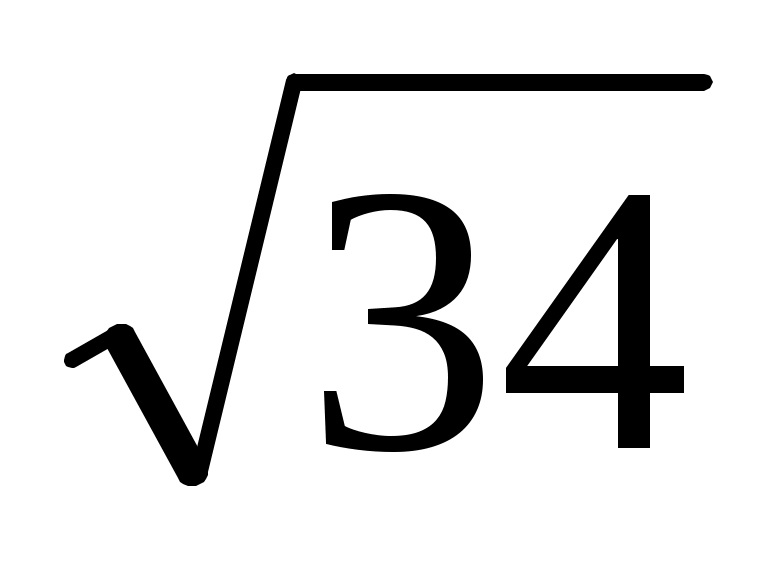 Н. Далее, Н. Далее,
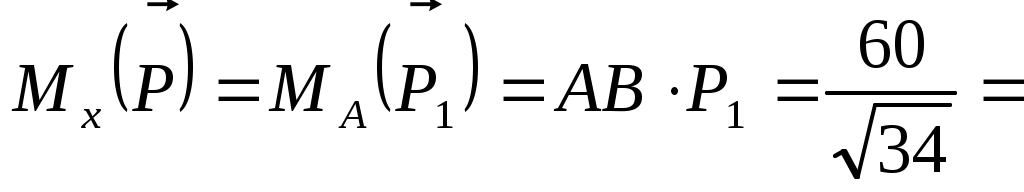 10,28 Н·см. 10,28 Н·см.
Найдем теперь 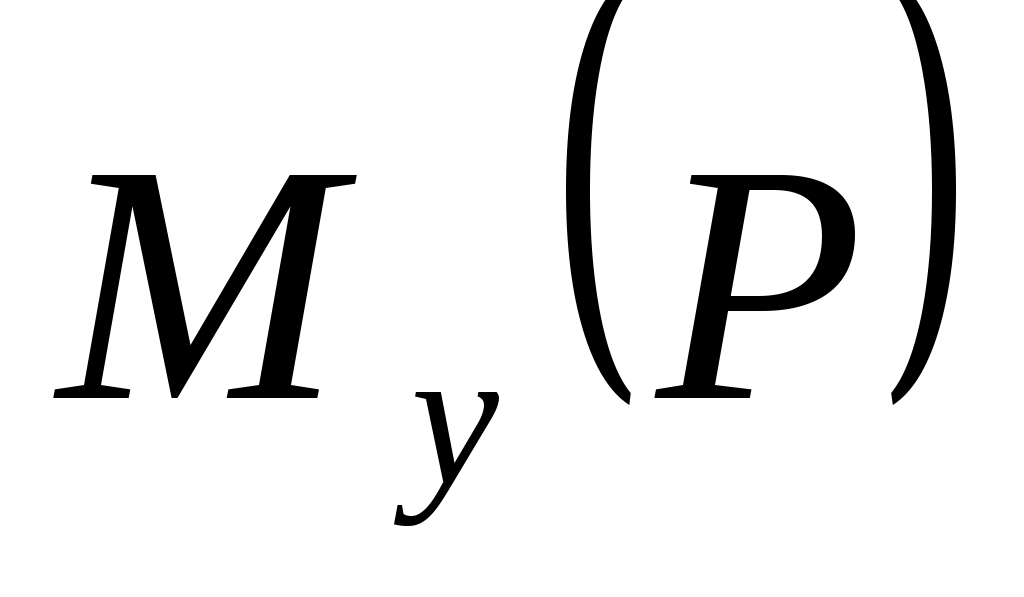 . Так как сила . Так как сила 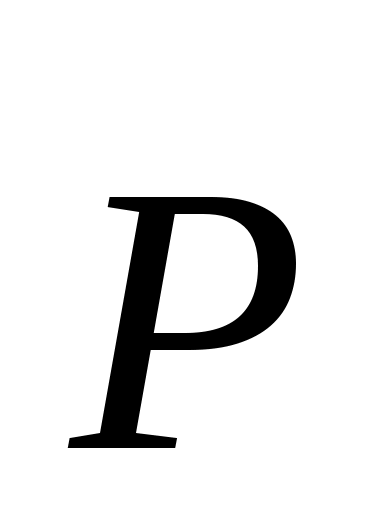 лежит в плос-кости ВЕКС, перпендикулярной оси Оу, то лежит в плос-кости ВЕКС, перпендикулярной оси Оу, то
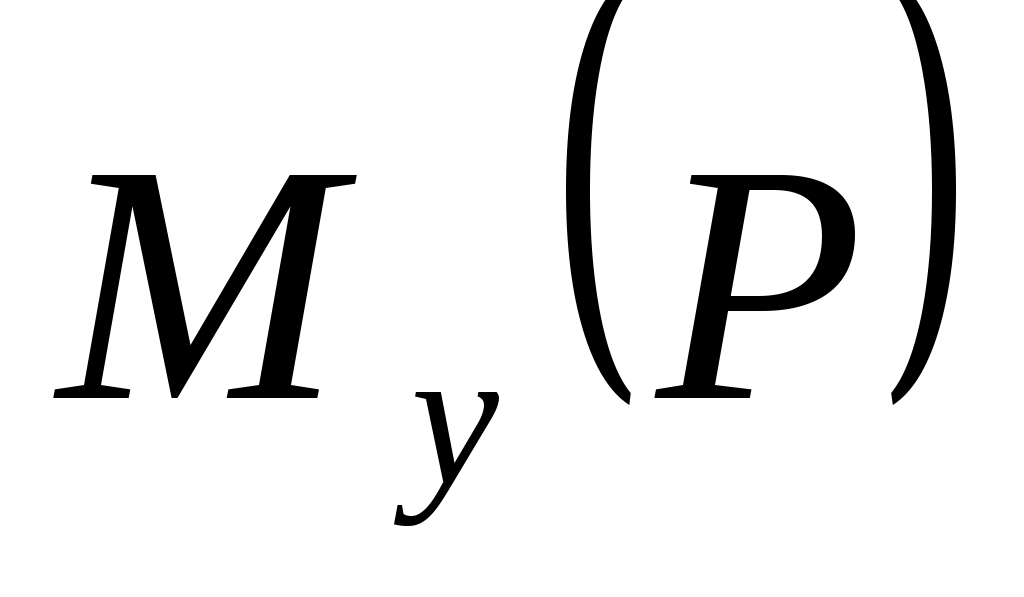 = =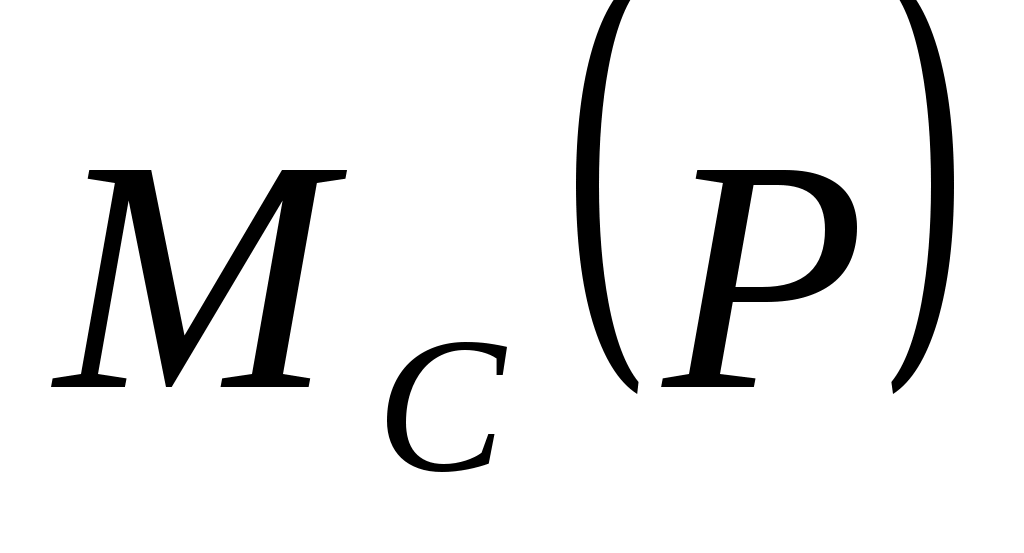 . .
В свою очередь,
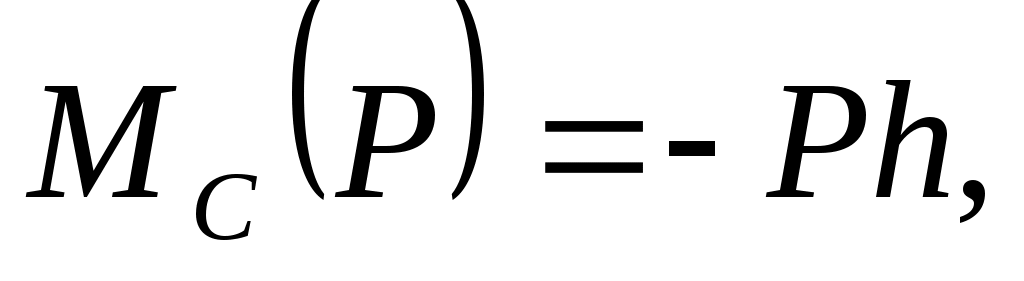
где h—длина перпендикуляра, опущенного из точки С на
линию действия силы Р.
Для определения h заметим, что
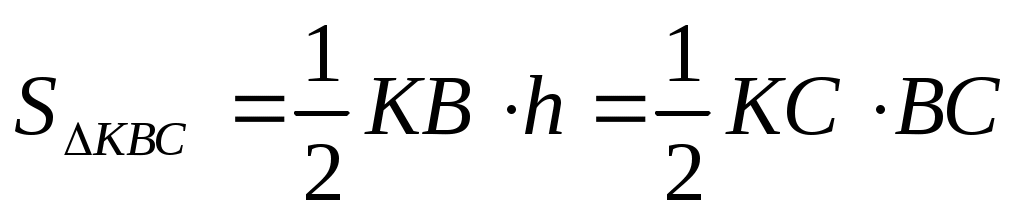 , ,
откуда
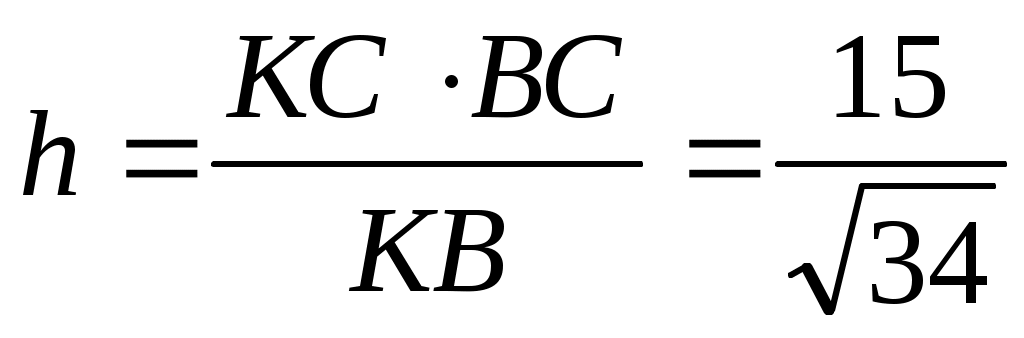 см. см.
Таким образом,
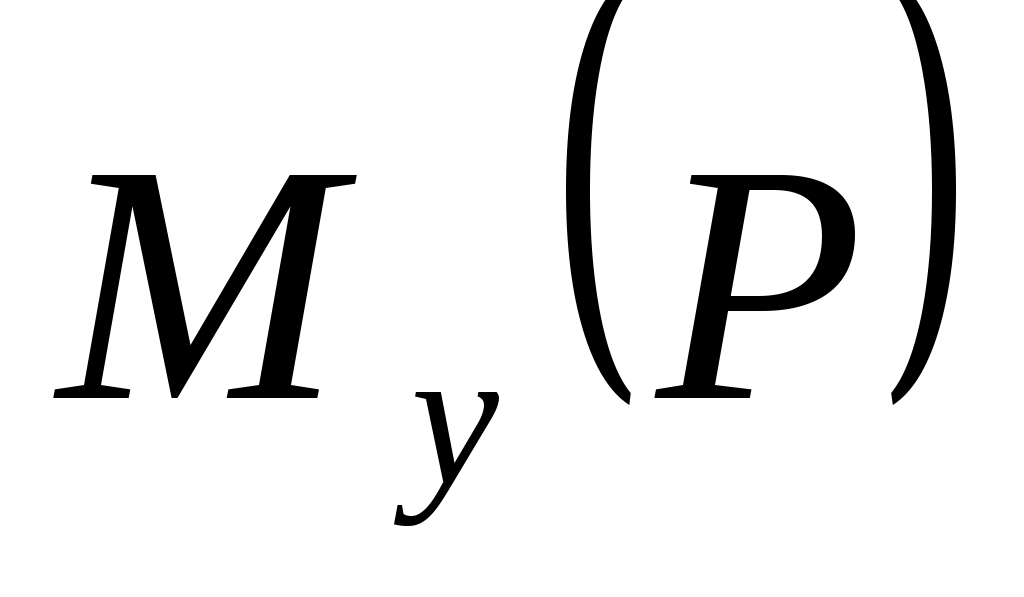 = =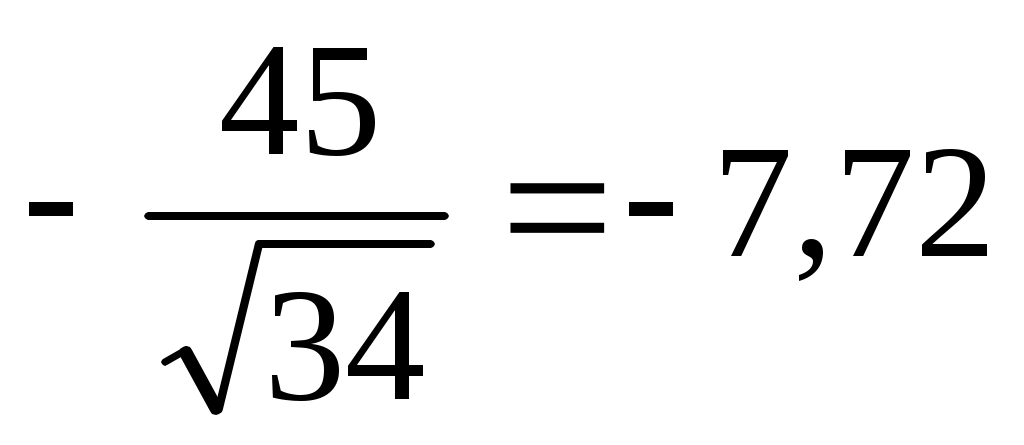 Н·см. Н·см.
Аналогично найдем
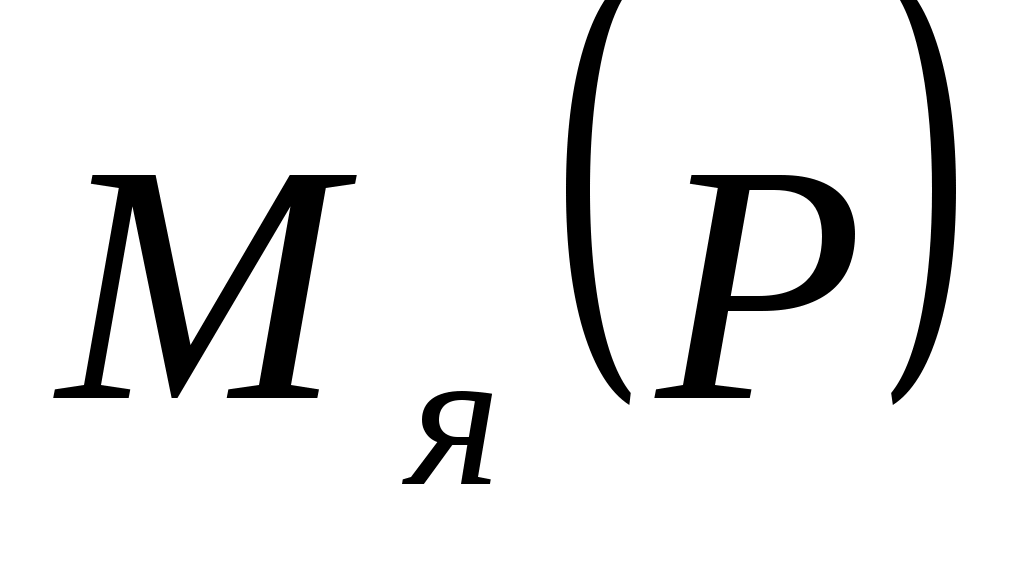 = =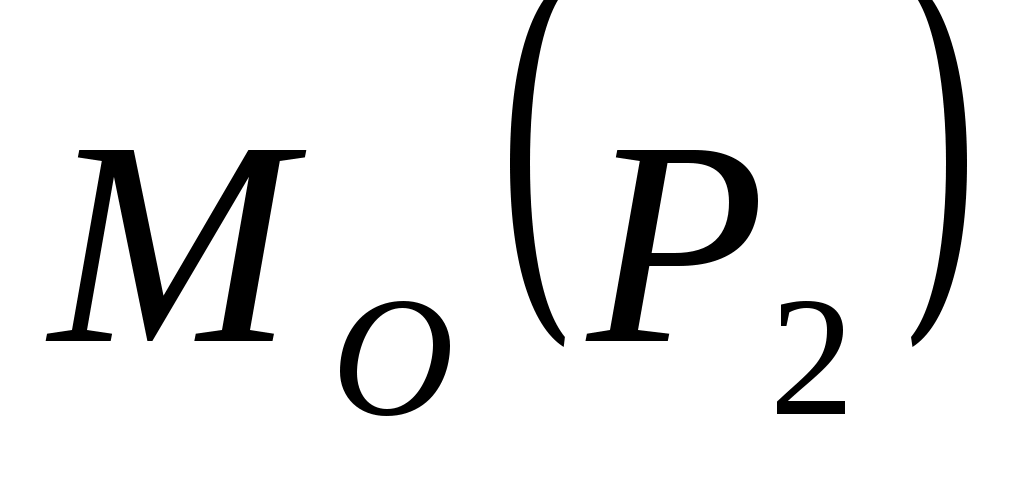 = =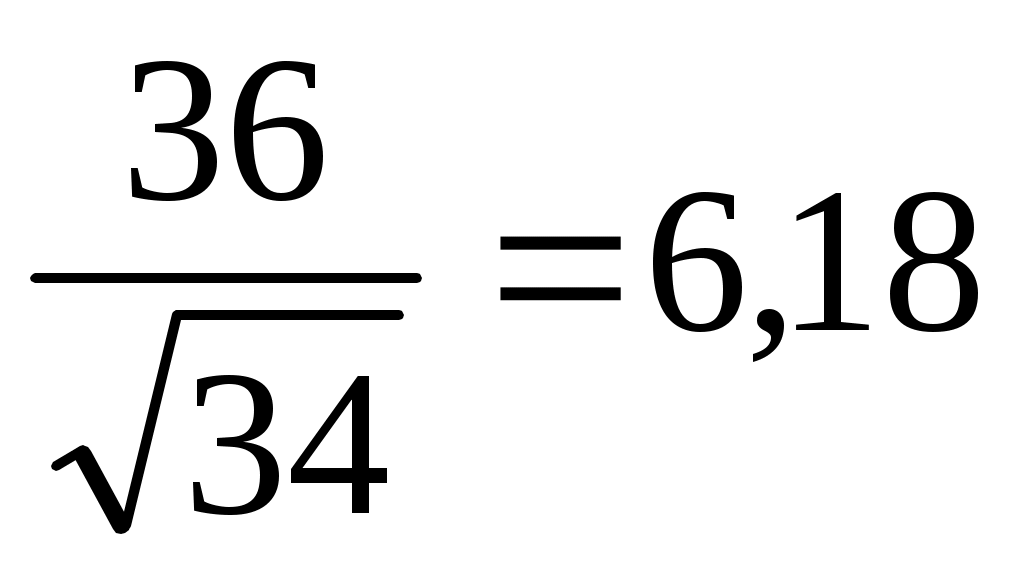 Н·см. Н·см.
Определим теперь 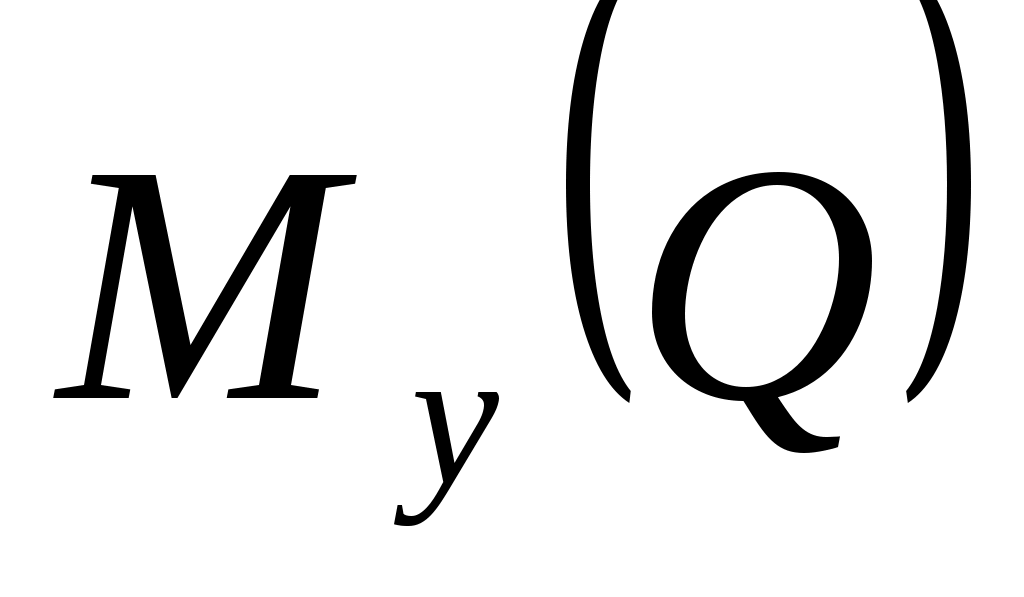 . Для этого проектируем силу . Для этого проектируем силу 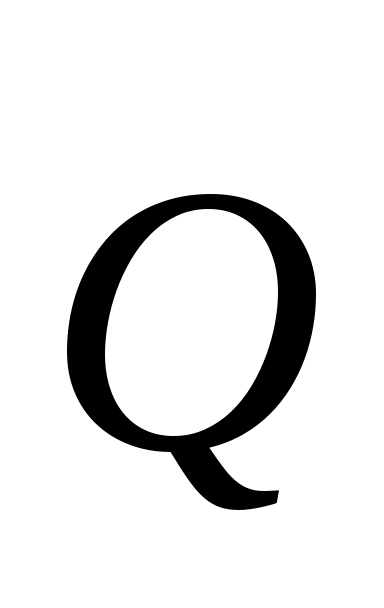 на плоскость LKCO, перпендикулярную оси Ох. Получим вектор на плоскость LKCO, перпендикулярную оси Ох. Получим вектор 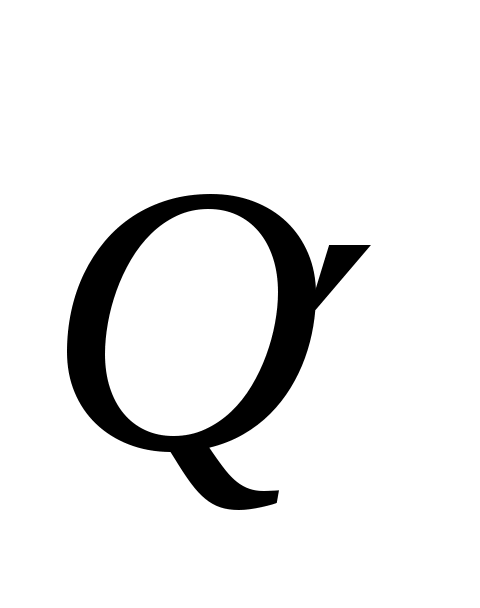 , направленный по диагонали LC и равный по модулю , направленный по диагонали LC и равный по модулю
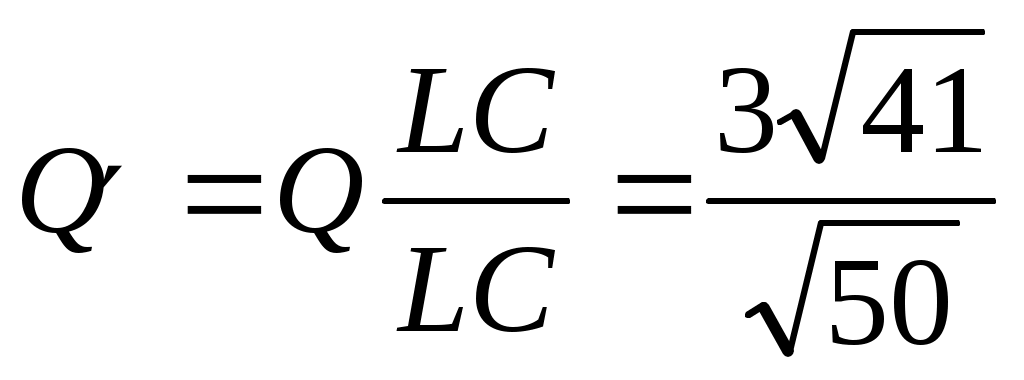 H. H.
Согласно определению момента
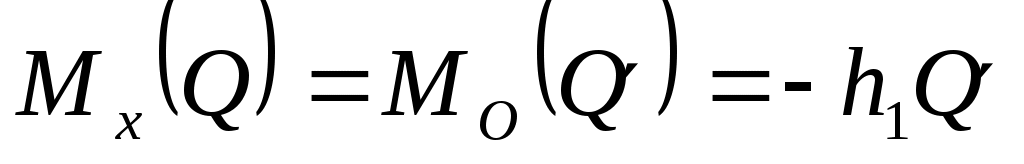 , ,
где h1 - длина перпендикуляра, опущенного из точки О на линию действия силы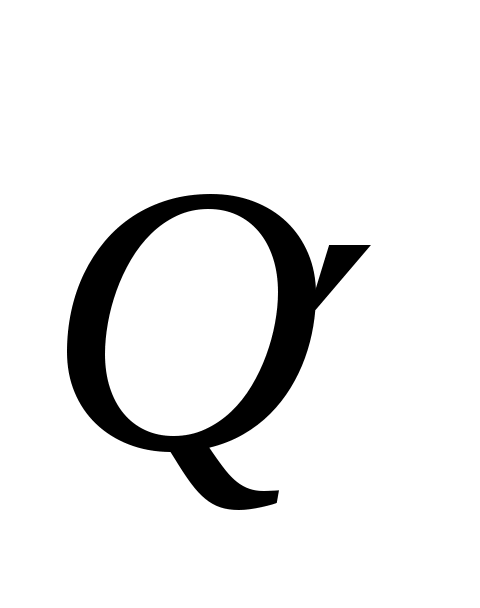 . .
Для определения h1 заметим, что
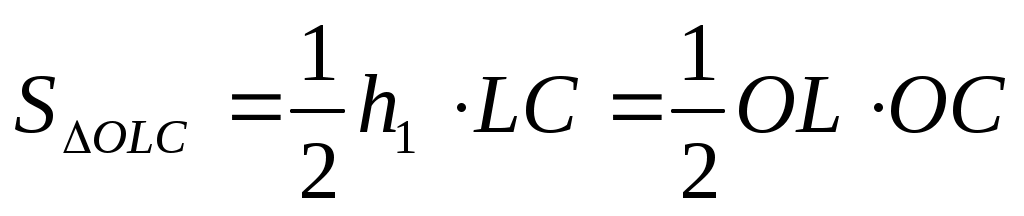 , ,
откуда
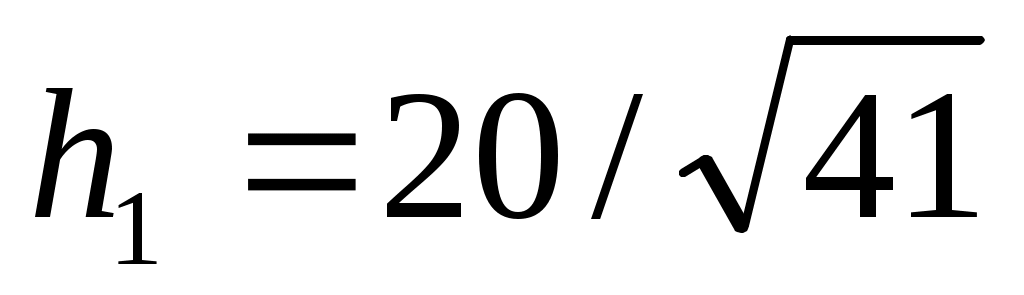 см.. см..
Таким образом,
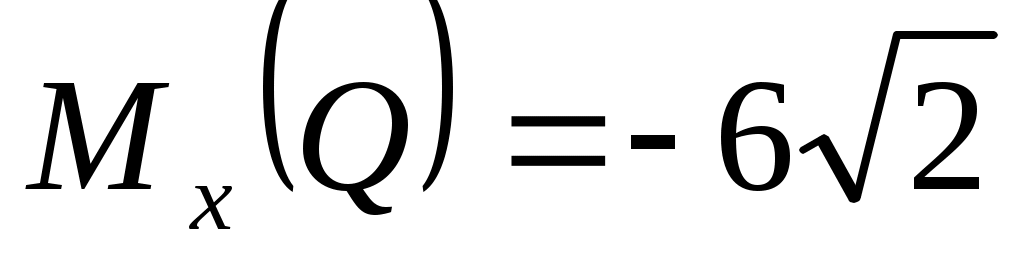 = - 8,49 Н·см.. = - 8,49 Н·см..
Аналогично найдем момент силы относительно оси Оу:
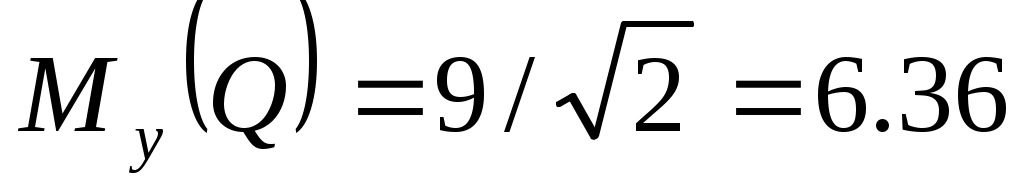 Н·см. Н·см.
Что касается 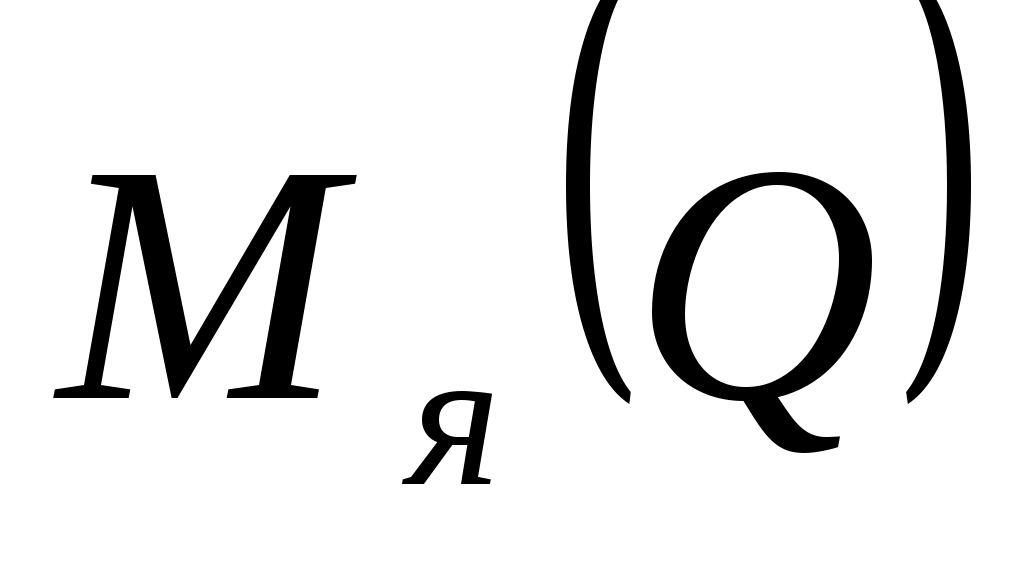 , то он равен нулю, так как линия действия силы , то он равен нулю, так как линия действия силы 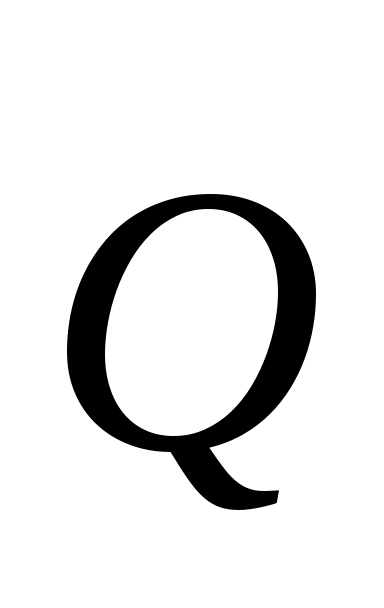 пересекает ось Оz. пересекает ось Оz.
Решим теперь эту задачу, используя теорему Вариньона. Для этого разложим силы на составляющие, параллельные осям. Так как 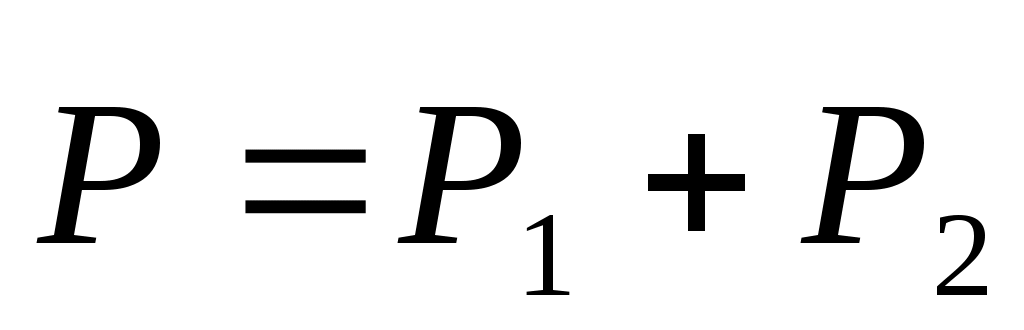 , то , то 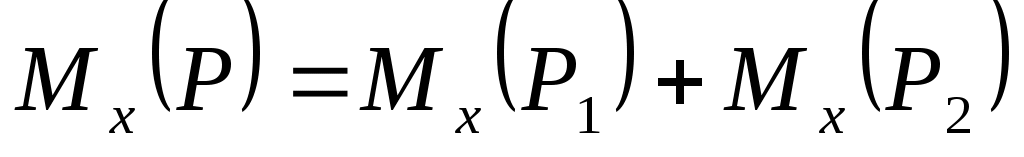 . .
Но 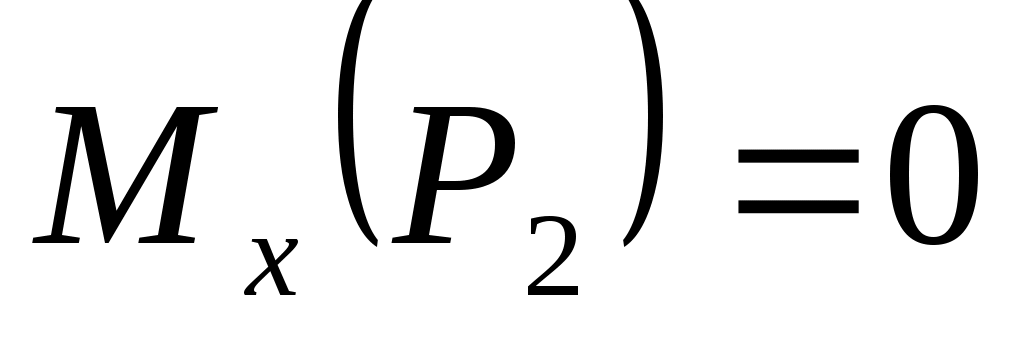 , так как линия действия силы , так как линия действия силы 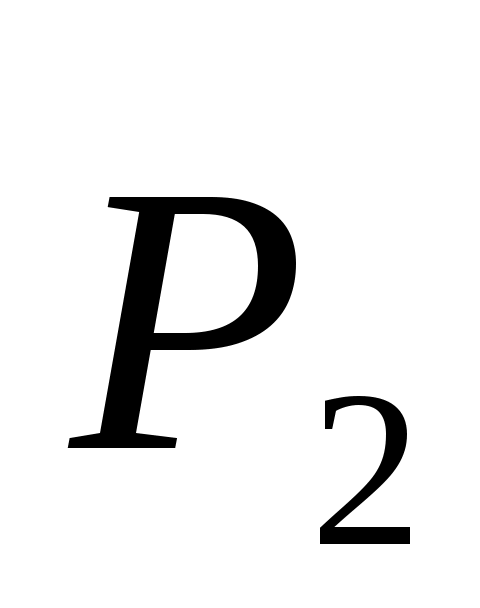 параллельна оси Ох, следовательно, параллельна оси Ох, следовательно,
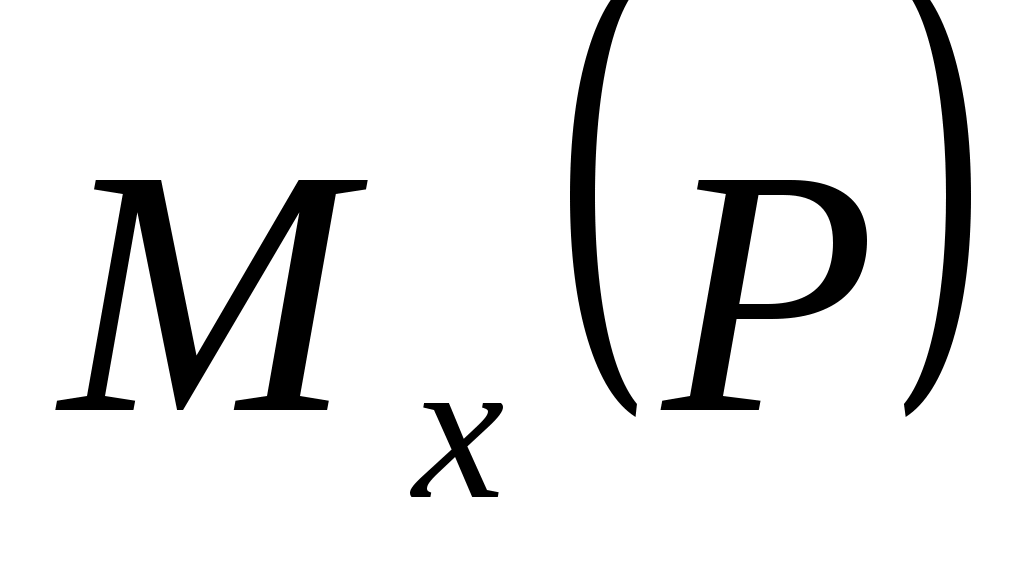 + +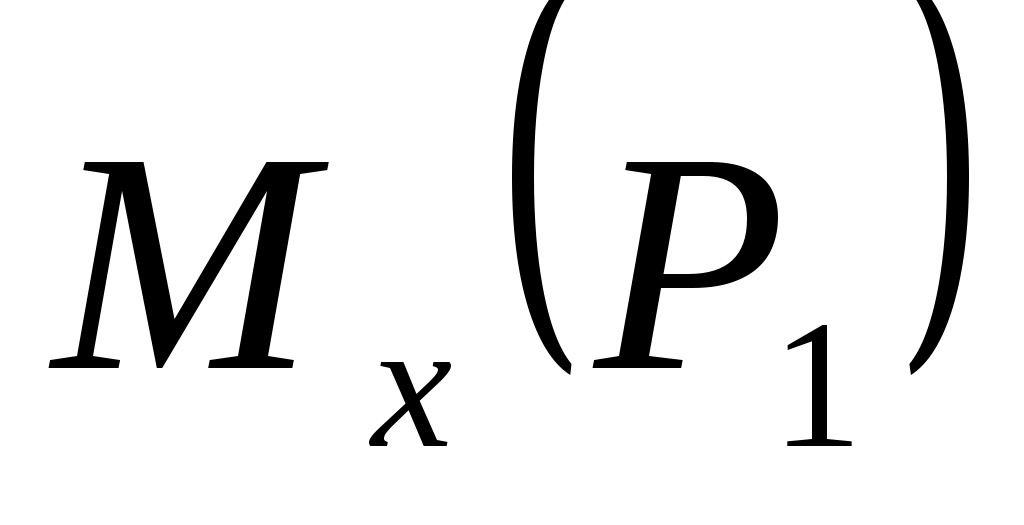 = АB·P1 = 10,28 Н·см. = АB·P1 = 10,28 Н·см.
Разложим теперь силу 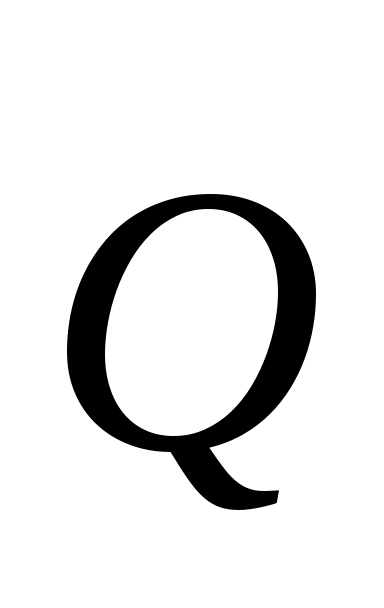 на составляющие, направленные параллельно координатным осям: на составляющие, направленные параллельно координатным осям: 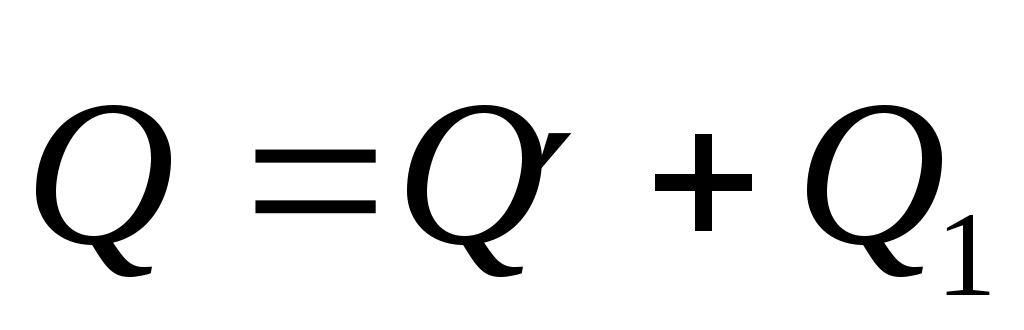 , где , где 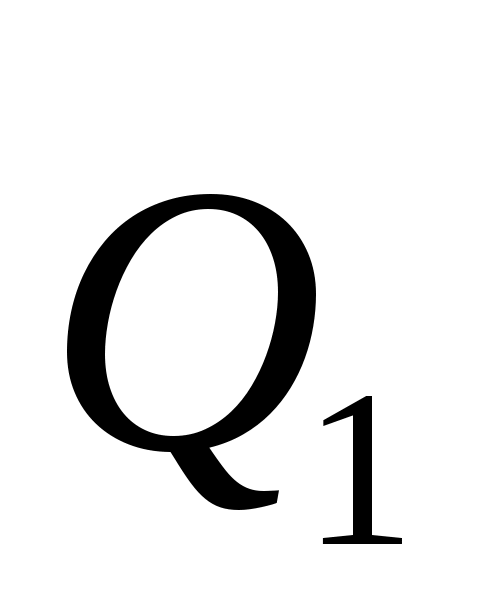 - составляющая, параллельная оси Ох. - составляющая, параллельная оси Ох.
Силу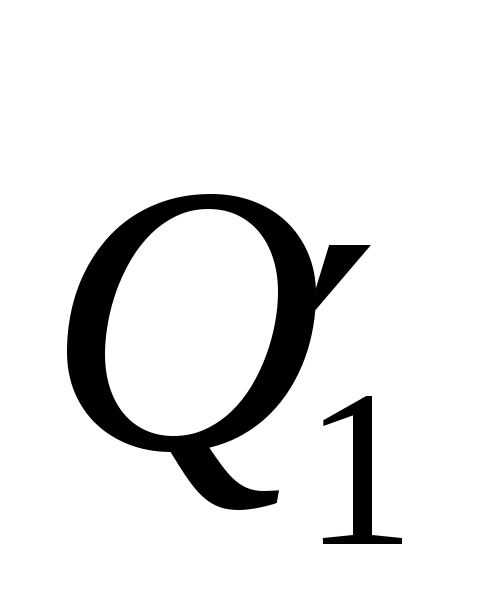 , направленную по диагонали LC, разложим на две составляющие: , направленную по диагонали LC, разложим на две составляющие: 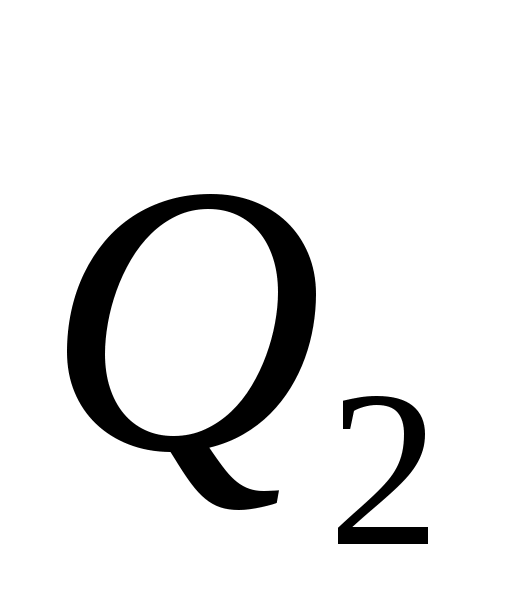 - пo линии LKи - - пo линии LKи - 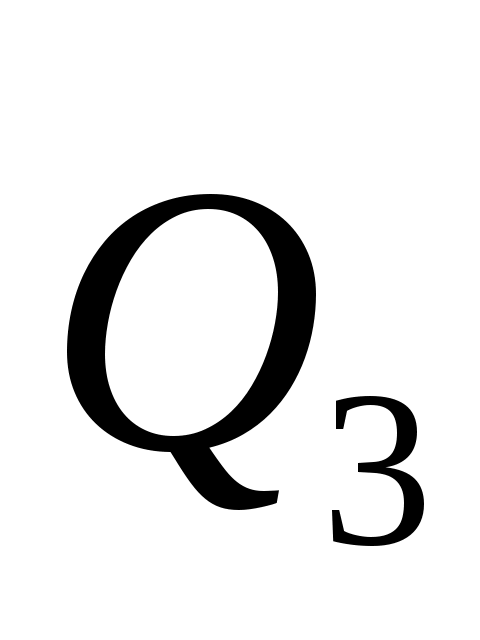 по линии LO. по линии LO.
Таким образом, 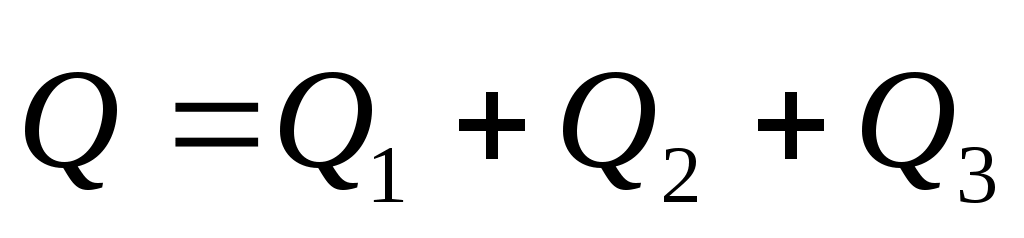 . .
Модуль Q1 определим из подобия треугольников:
Q1/Q = DL/LB,
откуда
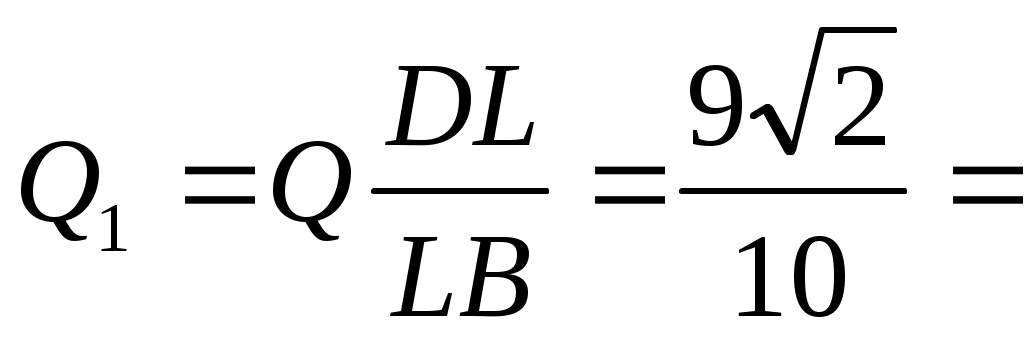 1,273 Н. 1,273 Н.
Далее найдем
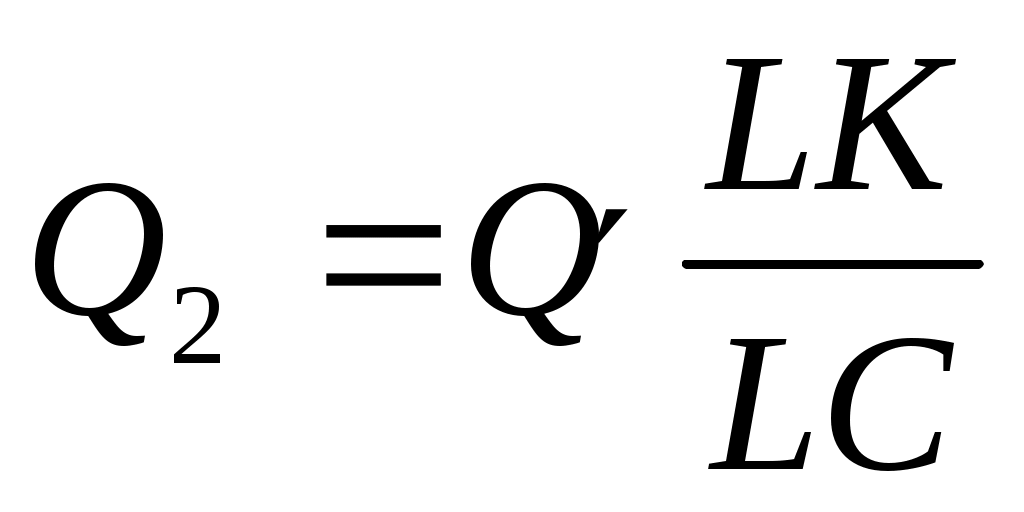 , ,
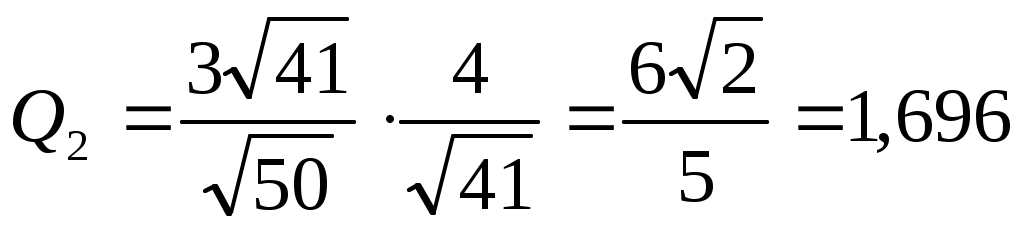 Н, Н,
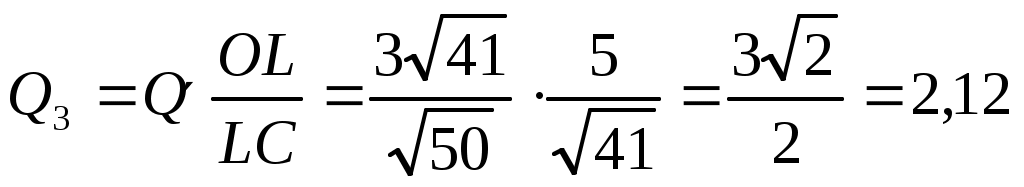 Н. Н.
По теореме Вариньона
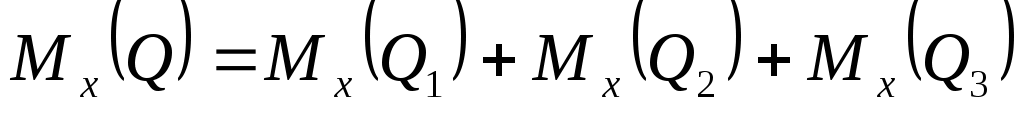 . .
Силы 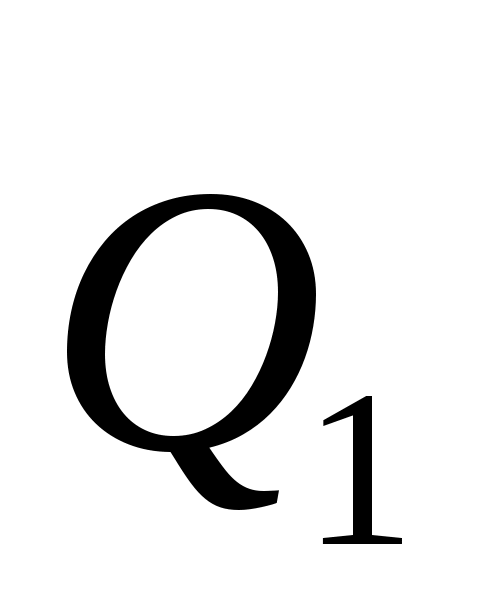 и и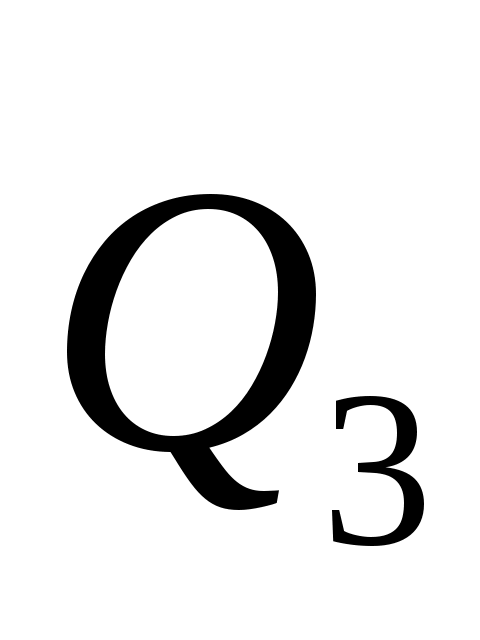 моментов относительно оси Ох не дают, следовательно, моментов относительно оси Ох не дают, следовательно,
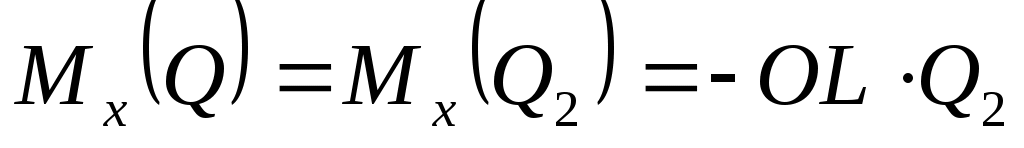 = - 8,49 Н·см. = - 8,49 Н·см.
Аналогично определяют моменты относительно других осей. Эту же задачу можно решить, используя формулы (12). Предварительно найдем проекции силы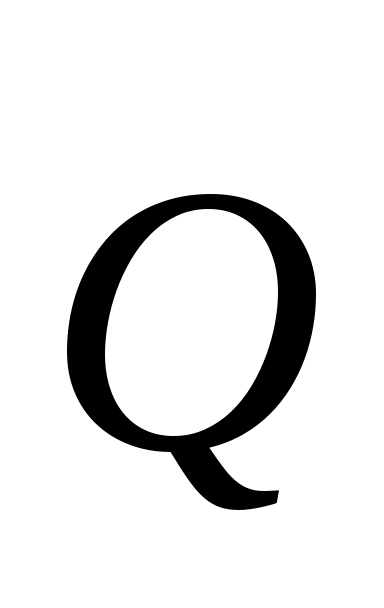 : :
Qx= Q1; Qy= Q2; Qz= - Q3
и координаты точки ее приложения: xL = 0; уL= 0; zL= 5. По формуле (12)
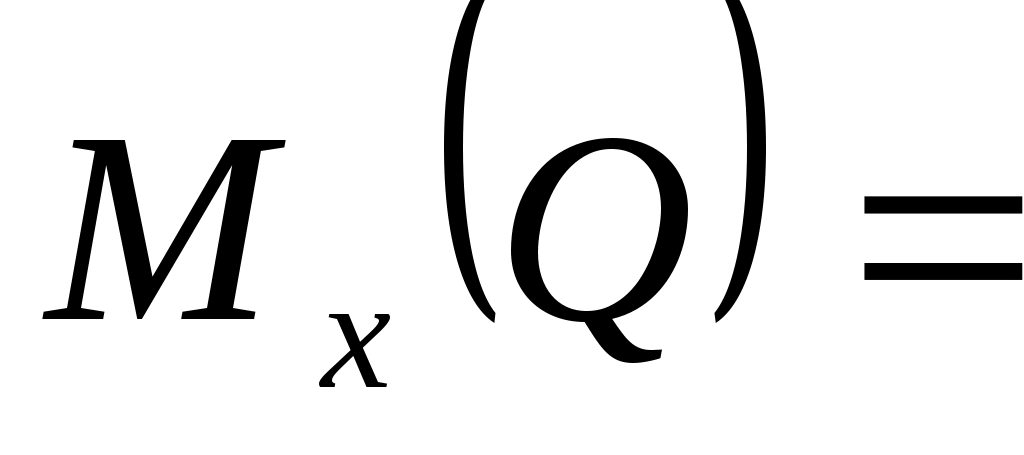 - yLQ3 - zLQ2= - 6 - yLQ3 - zLQ2= - 6 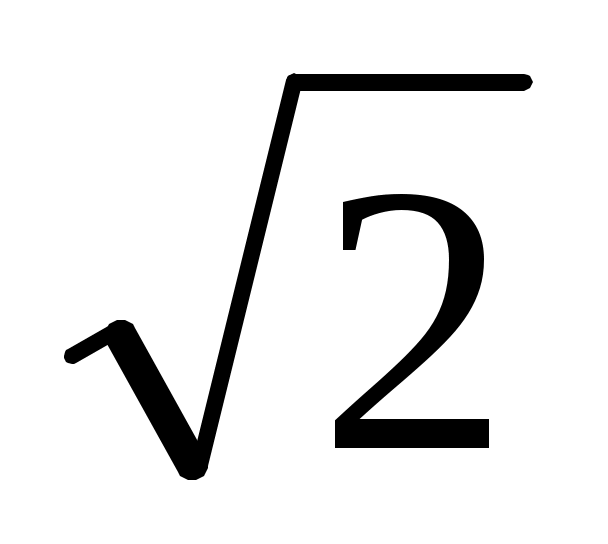 = - 8,49 Н·см, = - 8,49 Н·см,
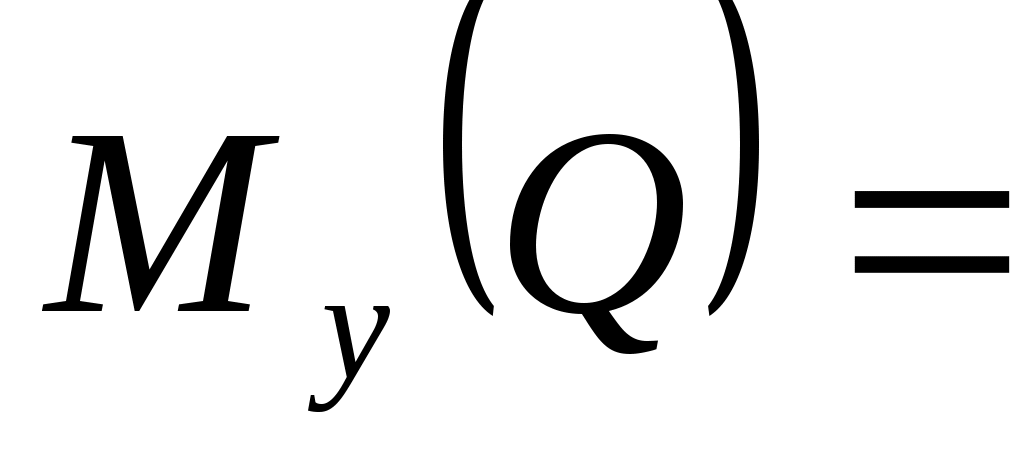 zLQ1 + xLQ3 = 6,38 Н·см. zLQ1 + xLQ3 = 6,38 Н·см.
Аналогично находят остальные моменты.
Задачи
Момент силы относительно оси и точки
2.4.1. Определить модуль момента силы 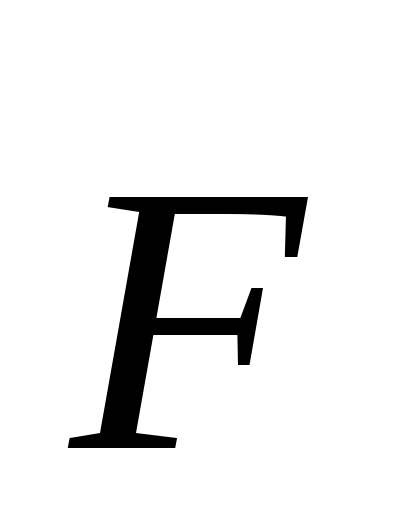 относи-тельно точки О, если задано: относи-тельно точки О, если задано: 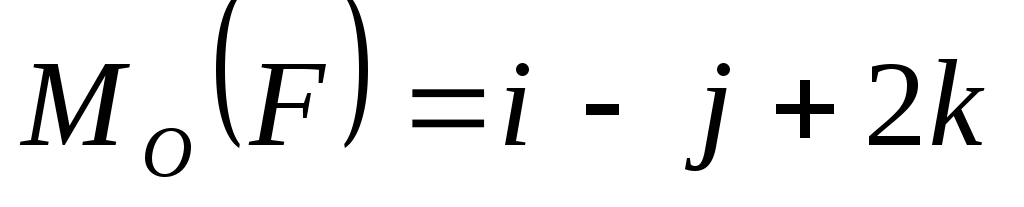 (2,45) (2,45)
2.4.2. Положение точки А в пространстве (рис. 309) определяется радиус-вектором (м) 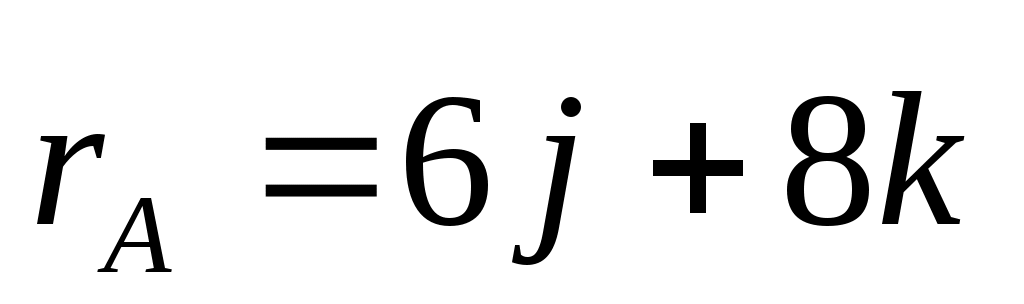 . К точке А приложена сила (Н) . К точке А приложена сила (Н) 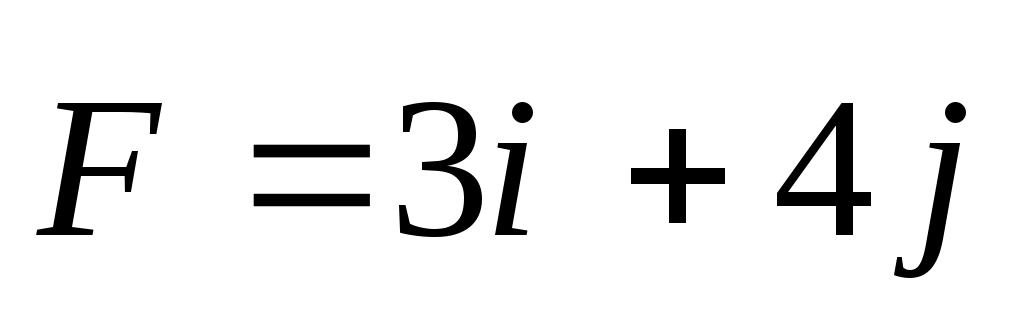 . Определить модуль момента этой силы относительно точки О. (43,9) . Определить модуль момента этой силы относительно точки О. (43,9)
2.4.3. Момент силы 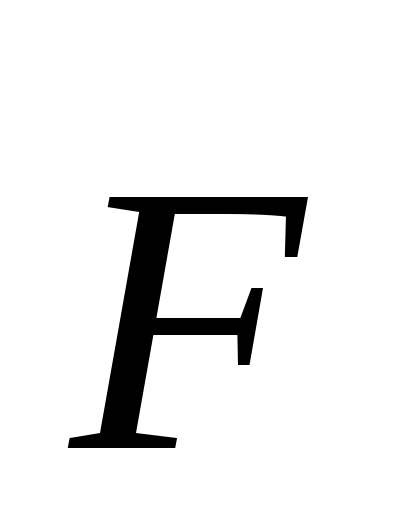 (рис. 310) относительно центра О равен МО( (рис. 310) относительно центра О равен МО(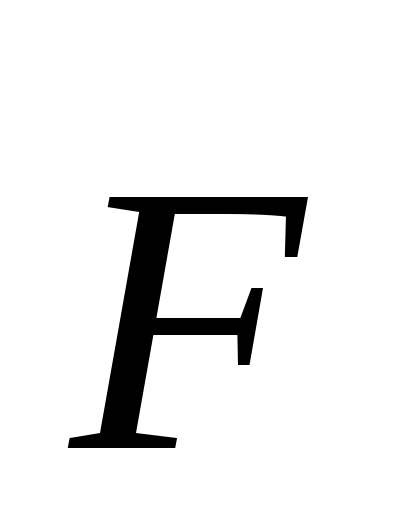 ) = 10 Н·м и образует с осями Ох и Оу углы α = 120° и β = 120°. Определить момент этой силы о ) = 10 Н·м и образует с осями Ох и Оу углы α = 120° и β = 120°. Определить момент этой силы о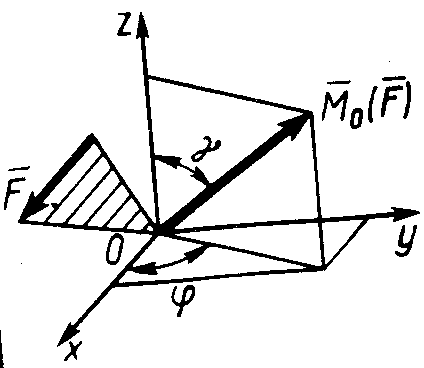 тносительно оси Ох. (-5) тносительно оси Ох. (-5)
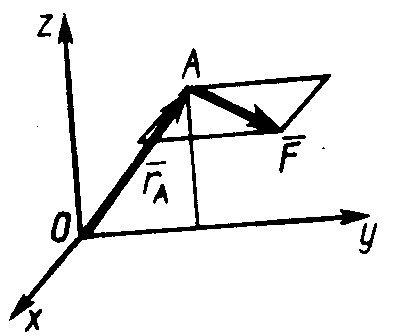 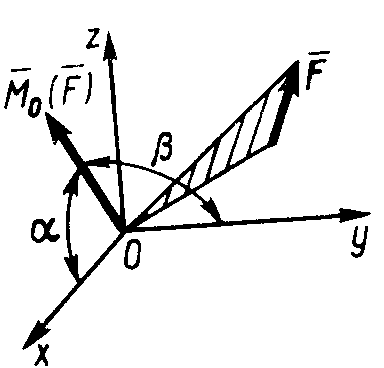
Рис. 309 Рис. 310 Рис. 311
2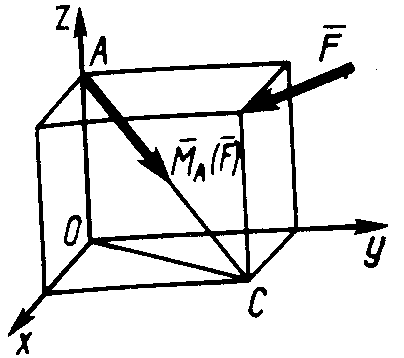 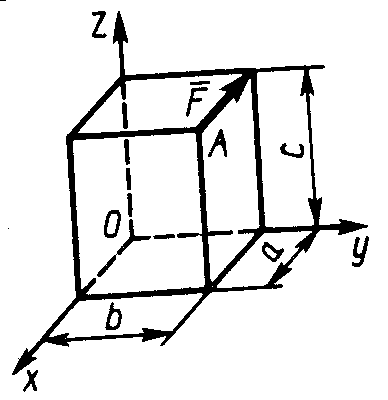 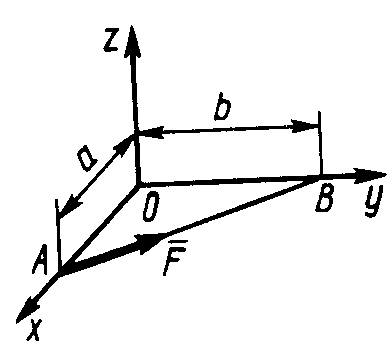 .4.4. Момент силы .4.4. Момент силы 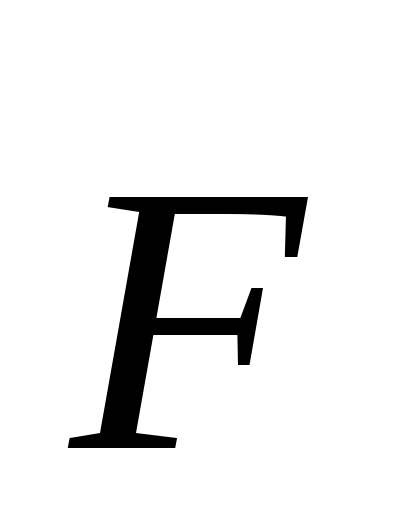 (рис. 311) относительно центра О равен МО( (рис. 311) относительно центра О равен МО(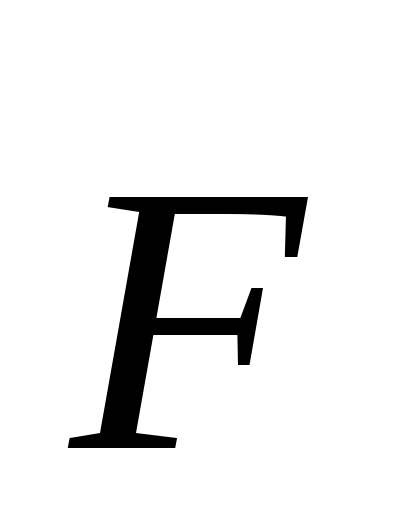 ) = 100 Н·м и расположен в пространстве так, что углы γ = 30° и φ = 30° . Определить момент этой силы относительно оси Оу. (25) ) = 100 Н·м и расположен в пространстве так, что углы γ = 30° и φ = 30° . Определить момент этой силы относительно оси Оу. (25)
Рис. 312 Рис. 313 Рис. 314
2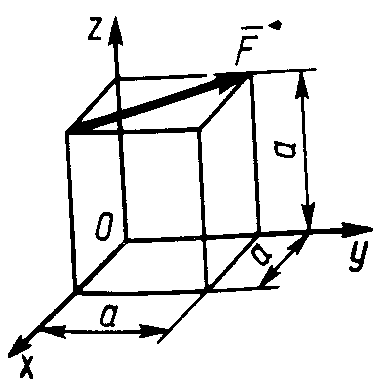 .4.5. Момент силы .4.5. Момент силы 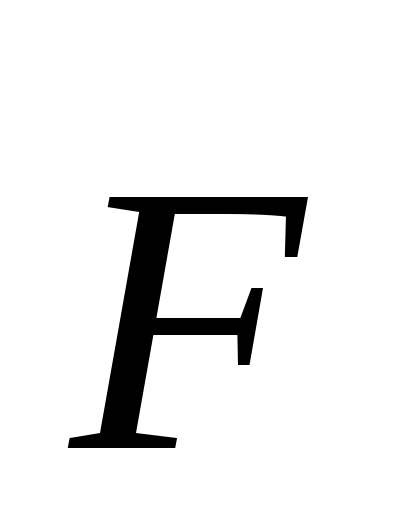 (рис. 312) относительно точки А по модулю равен МО( (рис. 312) относительно точки А по модулю равен МО(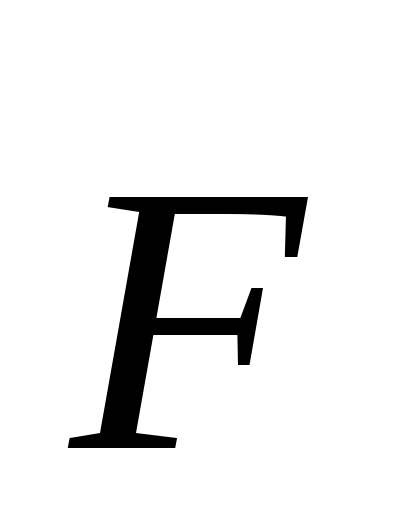 ) = 50 Н·м и направлен по диагонали АС параллелепипеда. Определить момент этой силы относительно оси Оz, если ОА = 0,3 м и АС = 0,5 ) = 50 Н·м и направлен по диагонали АС параллелепипеда. Определить момент этой силы относительно оси Оz, если ОА = 0,3 м и АС = 0,5
Рис. 315 м. (-30)
2.4.6. К точке А прямоугольного параллелепипеда (рис. 313) приложена сила F = 4 кН. Определить момент этой силы относительно оси Оу, если размеры а = 10 м, b = 6 м, с = 20 м. (-8 ·104)
2.4.7. Определить момент силы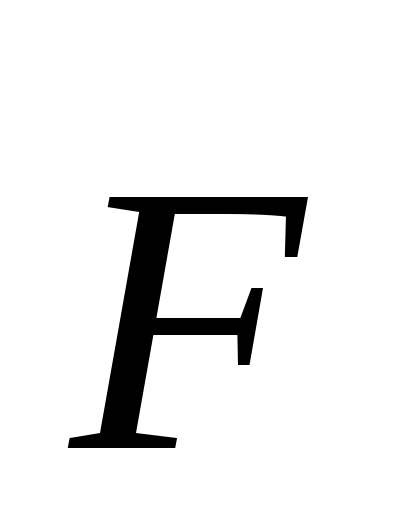 (рис. рис. 314) относительно оси Ох, если сила F = 20 Н пересекает оси Ох и Оу на расстояниях а = 2 м и b = 3 м. (0) (рис. рис. 314) относительно оси Ох, если сила F = 20 Н пересекает оси Ох и Оу на расстояниях а = 2 м и b = 3 м. (0)
2.4.8. Определить момент силы (рис. 315) относительно оси Ох, если ее значение F = 16 Н, ребро куба а = 0,75 м. (-8,49) (рис. 315) относительно оси Ох, если ее значение F = 16 Н, ребро куба а = 0,75 м. (-8,49) Равновесие пространственной системы параллельных сил
2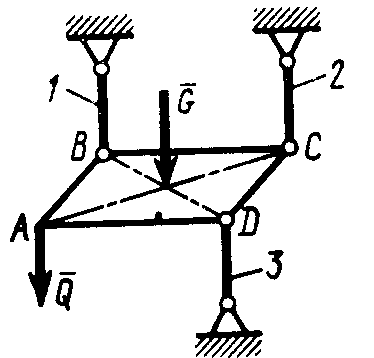 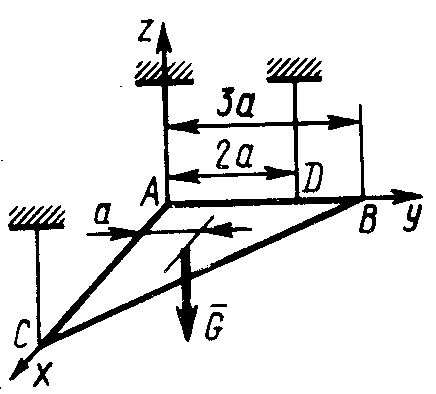 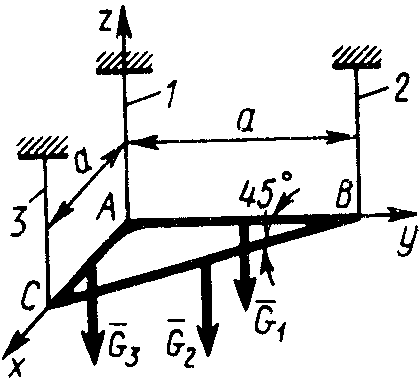 .4.9. Квадратная пластина ABCD (рис. 316) весом G = 115 Н в горизонтальном положении закреплена шарнирно в трех вертикальных стержнях 1, 2 и 3. В точке А приложена вертикальная сила Q = 185 Н. Из уравнения равновесия моментов сил относительно оси BD определить усилие в стержне 2. (-185) .4.9. Квадратная пластина ABCD (рис. 316) весом G = 115 Н в горизонтальном положении закреплена шарнирно в трех вертикальных стержнях 1, 2 и 3. В точке А приложена вертикальная сила Q = 185 Н. Из уравнения равновесия моментов сил относительно оси BD определить усилие в стержне 2. (-185)
Рис. 316 Рис. 317 Рис. 318
2.4.10. Однородная пластина (рис. 317) весом G = 500 Н в форме прямоугольного треугольника АВС в горизонтальном положении висит на трех веревках, закрепленных в точках А, С и D. Определить натяжение веревки, привязанной в точке D, если расстояние а = 1 м. (250)
2.4.11. Однородная треугольная сварная рама АВС (рис. 318) в горизонтальном положении удерживается тремя вертикальными тросами 1, 2 и 3. Определить натяжение троса 3, если вес частей рамы G1 = G3 = 101 Н, G2 = 143 Н. (122)
2.4.12. Пластинка ABCD (рис. 319) закреплена в горизонтальном положении с помощью шарниров и трех стержней 1, 2 и 3. Вес пластинки G1 = 10 Н. В точках А и Dк пластинке шарнирно подвешена вторая пластинка шириной EF = AD и весом G2= 8 Н. Определить усилие в стержне 1, если расстояние а = 0,4 м. (-4)
2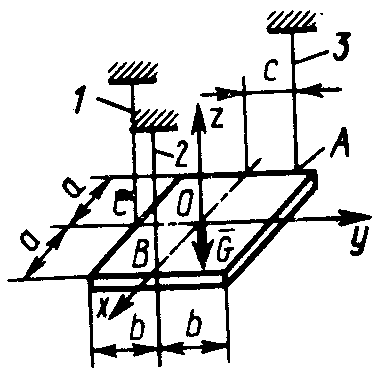 .4.13. Прямоугольная однородная пластинка закреплена горизонтально(рис. 320) с помощью трех нитей 1, 2 и 3, закрепленных в точках А, В и С. Определить расстояние с расположения точки А от оси симметрии, при котором нити будут натянуты одинаково, если вес пластинки G = 3Н, расстояния а = 0,2 м и b = 0,1 м. (0,1) .4.13. Прямоугольная однородная пластинка закреплена горизонтально(рис. 320) с помощью трех нитей 1, 2 и 3, закрепленных в точках А, В и С. Определить расстояние с расположения точки А от оси симметрии, при котором нити будут натянуты одинаково, если вес пластинки G = 3Н, расстояния а = 0,2 м и b = 0,1 м. (0,1)
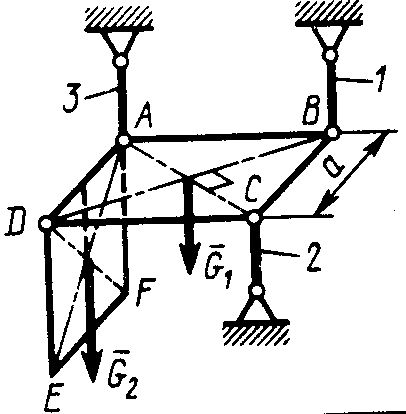 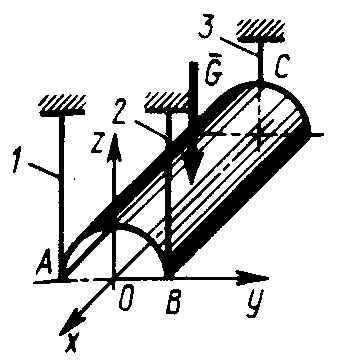
Рис. 319 Рис. 320 Рис. 321
2.4.14. Однородная оболочка весом G = 40 кН в виде полуцилиндра радиуса R висит на трех вертикальных тросах 1, 2 и 3, закрепленных в точках А, В и С (рис. 321). Определить в кН реакцию в тросе 1, если известно, что реакция в тросе 3 равна 20 кН. (10)
2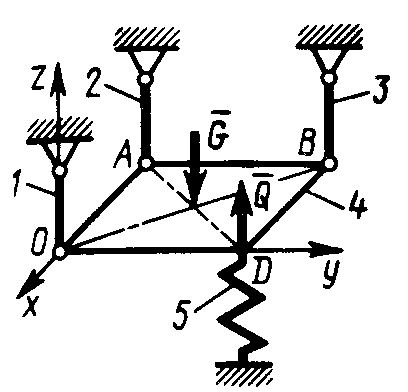 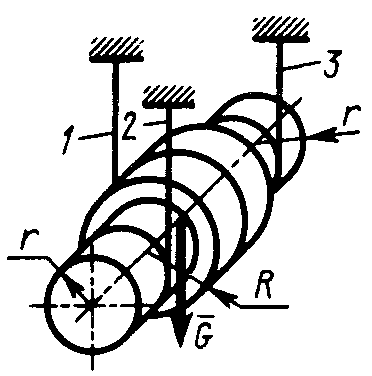 .4.15. На трех вертикальных стержнях 1, 2 и 3 шарнирно закреплена горизонтальная прямоугольная платформа 4 с размерами ОА = 1,5 АВ и весом G = 1 кН (рис. 322). В точке Dна платформу давит пружина 5 с силой Q = 0,5 кН. Определить в кН реакцию в стержне 2. (0,5) .4.15. На трех вертикальных стержнях 1, 2 и 3 шарнирно закреплена горизонтальная прямоугольная платформа 4 с размерами ОА = 1,5 АВ и весом G = 1 кН (рис. 322). В точке Dна платформу давит пружина 5 с силой Q = 0,5 кН. Определить в кН реакцию в стержне 2. (0,5)
Рис. 322 Рис. 323
2.4.16. Вал весом G = 6 кН (рис. 323) удерживается в горизонтальном положении вертикальными тросами 1, 2 и 3, намотанными на цилиндрические части вала, радиусы которых r = 0,1 м и R = 0,14 м. Зная, что натяжения тросов 2 и 3 T2 = T3 = 1,75 кН, определить натяжение троса 1. (2,5·103)
Равновесие произвольной пространственной системы сил
2.4.17*. Груз весом Р = 2 кН, подвешенный на нерастяжимой веревке, равномерно поднимается при помощи ворота радиусом r= 20 см, приводимого в движение бесконечной цепью, надетой на колесо радиусом R = 50 см (рис. 324). Размеры на чертеже даны в сантиметрах. Веревка сходит с ворота по горизонтали, силы натяжения ветвей цепи 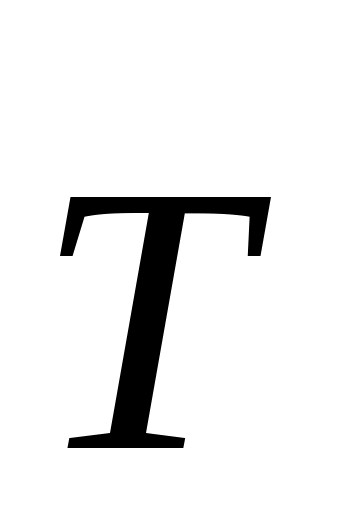 и и 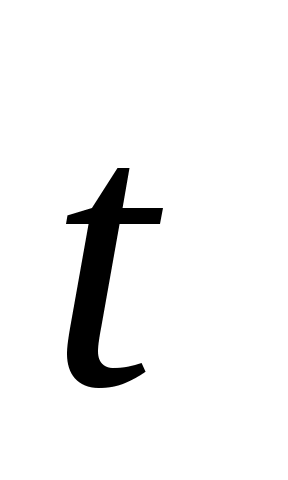 составляют с вертикалью углы α = 30°. Найти реакции подшипников А и В натяжения Т иt,если Т = 2t. составляют с вертикалью углы α = 30°. Найти реакции подшипников А и В натяжения Т иt,если Т = 2t.
Ответ:t = 0,8 кН, ХA = 0,6 кН, ZA= 1,04 кН, XB = 0,2 кН, ZB = 1,04 кН.
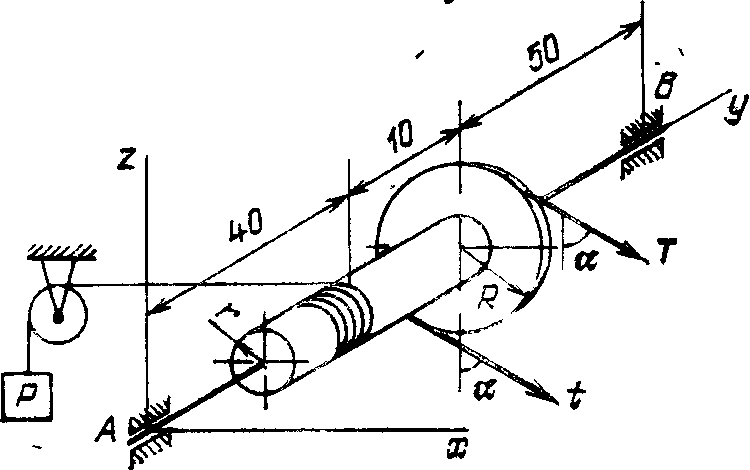
Рис. 324
2.4.18*. Груз Q = 2 кН равномерно поднимается при помощи ворота (рис. 325). Рукоятка КЕ перпендикулярна оси АВ ворота. Сила Р лежит в плоскости, перпендикулярной оси АВ и составляет угол 30° с вертикалью. К колесу D в плоскости, перпендикулярной оси АВ, приложена пара сил с моментом М =20 кН·см. Размеры на чертеже даны в сантиметрах, r= 10 cм. Найти силу Р и реакции подшипников А и В.
Ответ: Р = 3,08 кН, YA = 1,85 кН, ZA= 4,8 кН,
YB = - 0,31 кН, ZB = - 0,13 кН.
2.4.19*. Горизонтальный невесомый стержень АВ прикреплен к стене сферическим шарниром А и удержи-вается в положении равновесия двумя растяжками КЕ и CD (рис. 326). К стержню подвешен груз весом Р = 180 Н. Дано α= 30°, β = 60°, АЕ = ЕС = AB/3, АС = AD1. Найти реакции шарнира А и натяжение растяжек КЕ и CD.
Ответ: ТС = 312 Н, TЕ = 441 Н, ХА = - 110 Н, Уа= 491 Н, ZA = - 90 Н.
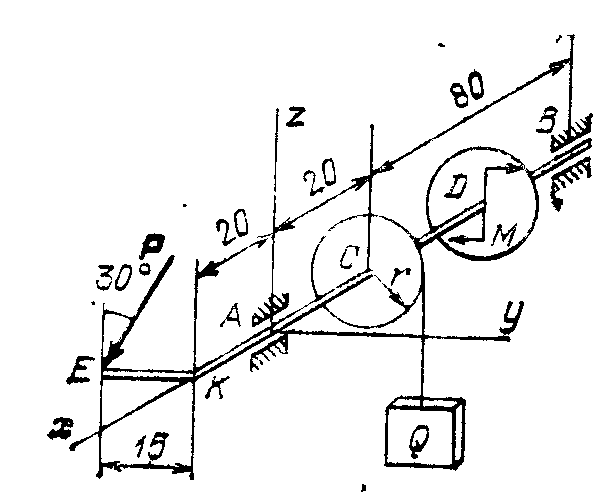
Рис. 325
2.4.20. Сколько уравнений равновесия имеет произвольная пространственная система сил? (б)
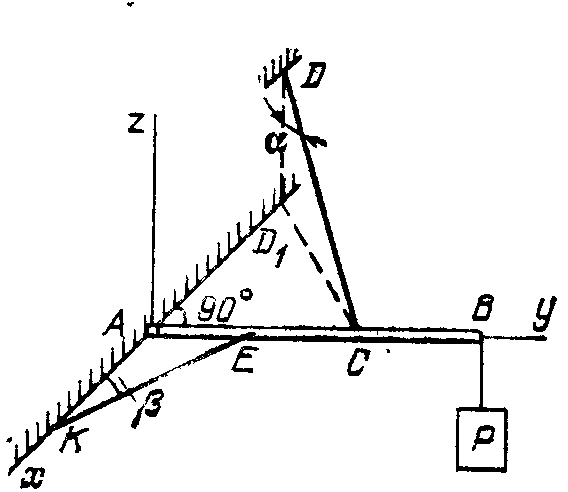
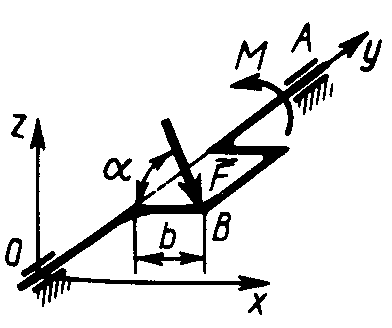
Рис. 326 Рис. 327
2.4.21. К коленчатому валу ОА (рис. 327) в точке В под углом α = 60° к горизонту приложена сила F = 10 Н, которая уравновешивается парой сил с моментом М. Определить модуль момента, если сила 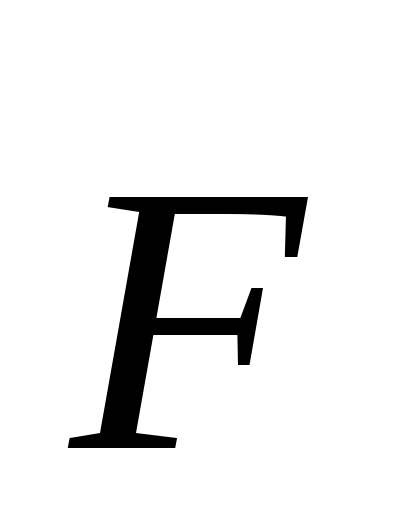 || Oxz и b = 0,9 м. (7,79) || Oxz и b = 0,9 м. (7,79)
2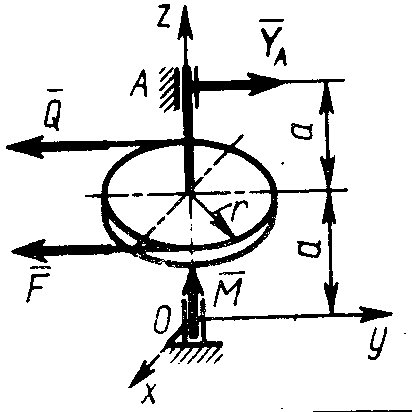 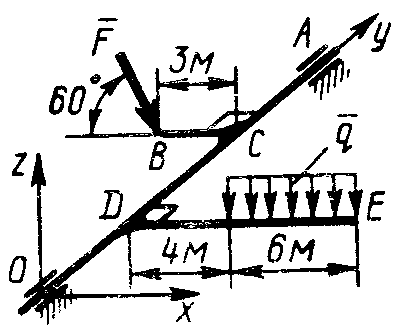 .4.22. К валу. ОА под прямым углом прикреплены стержни ВС и DE(рис. 328). К стержню DE приложена распределенная нагрузка q= 0,5 Н/м. Определить модуль силы, уравновешивающей данную нагрузку, если .4.22. К валу. ОА под прямым углом прикреплены стержни ВС и DE(рис. 328). К стержню DE приложена распределенная нагрузка q= 0,5 Н/м. Определить модуль силы, уравновешивающей данную нагрузку, если 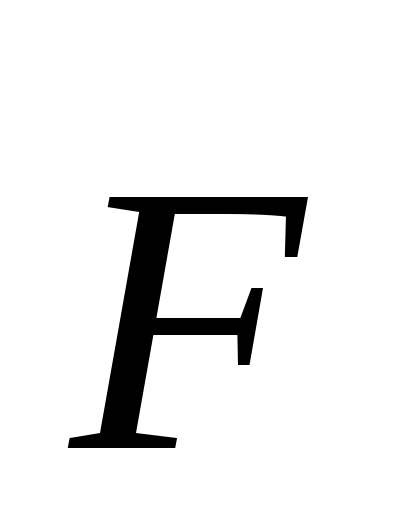 || Oxz. (8,08) || Oxz. (8,08)
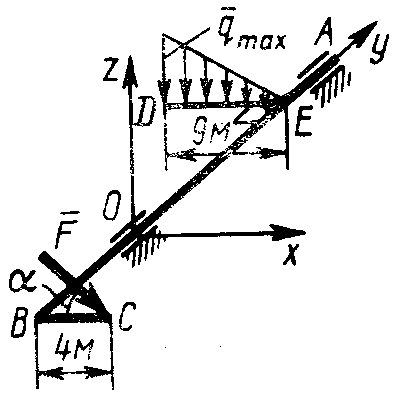
Рис. 328 Рис. 329 Рис. 330
2.4.23. К валу АОВ (рис. 329) под прямым углом прикреплены стержень DE, несущий распределенную нагрузку qmax = 0,5 Н/м, и стержень ВС. Нагрузка уравновешивается силой 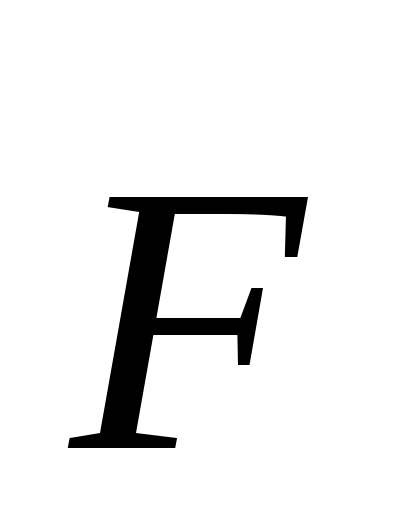 ||Oxz, приложенной к точке С под углом α = 30°. Определить модуль этой силы. (6,75) ||Oxz, приложенной к точке С под углом α = 30°. Определить модуль этой силы. (6,75)
2.4.24. Сила F = 2Q = 120 Н, приложенная к шкиву, уравновешивается парой сил с моментом М = 18 Н·м (рис. 330). Составив уравнение моментов сил относительно оси Ох, определить реакцию 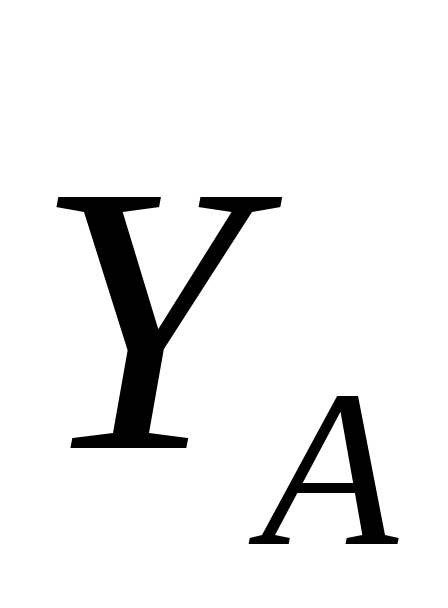 подшипника А, если радиус шкива r = 0,3 м, а = 0,3 м и сила подшипника А, если радиус шкива r = 0,3 м, а = 0,3 м и сила 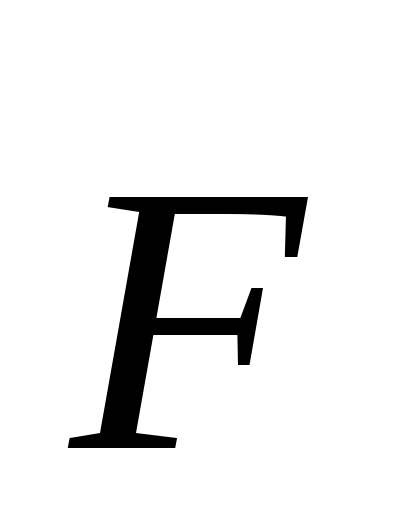 || || 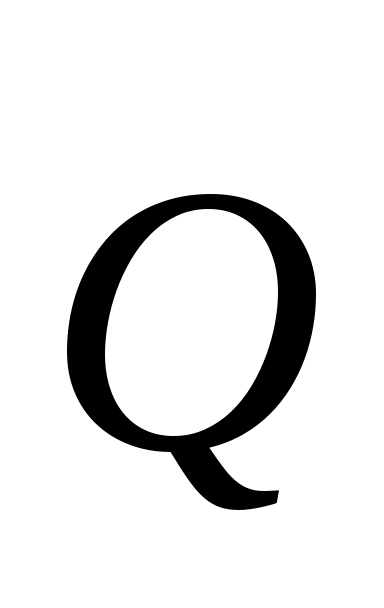 || Оу. (90) || Оу. (90)
2.4.25. Однородная плита ОАВС весом G = 30 Н (рис. 331) удерживается в горизонтальном положении шарнирами О, А и тросом BD. Определить натяжение троса, если а =2 м и угол α = 60°. (30)
2.4.26. Однородная квадратная рама ОАВС (рис. 332)со стороной а = 0,5 м и весом G = 140 Н под действием наложенных связей удерживается в горизонтальном положении. Составить уравнение моментов сил относительно линии ОВ и определить реакцию  шарнира А, если угол α = 60°.(0) шарнира А, если угол α = 60°.(0)
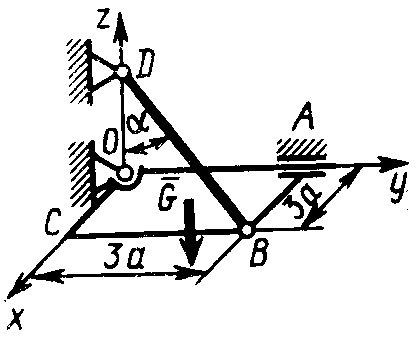 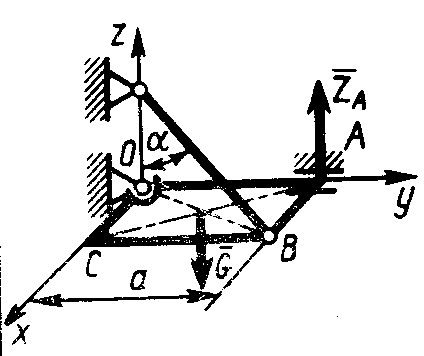
Рис. 331 Рис. 332
2.4.27. Однородное тело весом G = 60 Н (рис. 333) под действием наложенных связей находится в равновесии. Составив уравнение моментов сил относительно оси Ох, определить вертикальную составляющую реакции шарнира В, если размер а = 0,1 м. (40)
2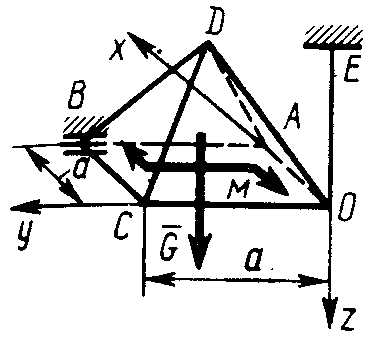 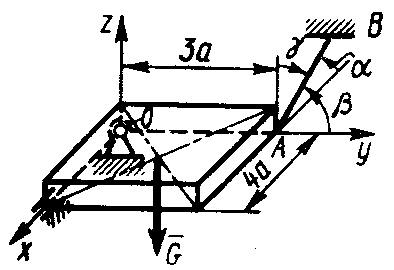 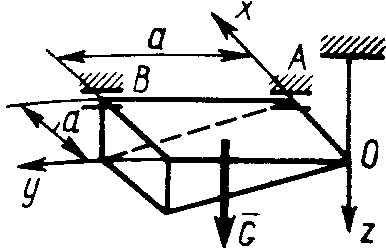 .4.28. Однородная пирамида OABCD весом G = 60 Н (рис. 334) под действием пары сил с моментом М = 150 Н·м и наложенных связей находится в равновесии. Определить составляющую реакции шарнира В, параллельную оси Ох, если размер а = 3 м, а пара сил лежит в плоскости Оху. (50) .4.28. Однородная пирамида OABCD весом G = 60 Н (рис. 334) под действием пары сил с моментом М = 150 Н·м и наложенных связей находится в равновесии. Определить составляющую реакции шарнира В, параллельную оси Ох, если размер а = 3 м, а пара сил лежит в плоскости Оху. (50)
Рис. 333 Рис. 334 Рис. 335
2.4.29. Однородная плита весом G = 400 Н под действием наложенных связей находится в равновесии (рис. 332). Составив уравнение моментов относительно оси Ох, определить натяжение троса АВ, если а = 20 см и углы α = 61°, β = 44°, γ = 60°. (400)
2.4.30. Тело весом G = 11 кН под действием наложенных связей и приложенной силы F = 3 кН находится в равновесии (рис. 336). Составить уравнение моментов сил относительно оси Ох, затем определить натяжение троса АВ, если размер а = 0,2м. (4·103)
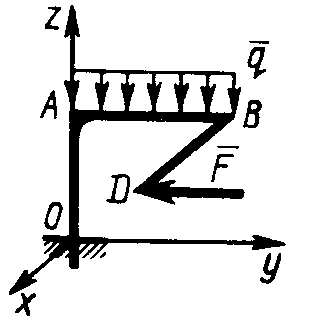
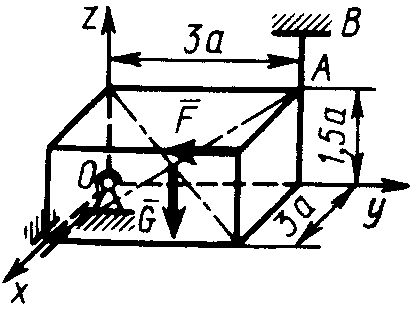
Рис. 336 Рис. 337
2.4.31. Фигурная балка OABD находится в равновесии (рис. 337). Определить в тоннах составляющую реакции заделки вдоль оси Oz, если дано:ОА = 1,7 м, АВ = 2 м,
BD = 3,4 м, BD || Ох,сила F = 1 т и интенсивность распределенной нагрузки q = 2 т/м. (4)
|
 Скачать 1.32 Mb.
Скачать 1.32 Mb.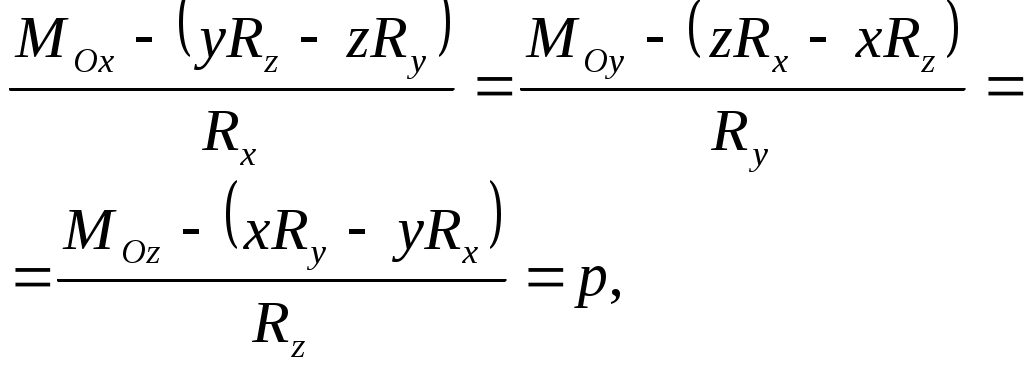 (67)
(67)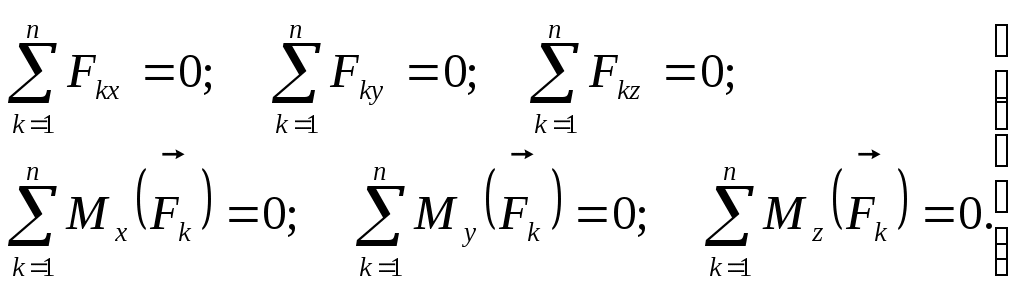 (68)
(68)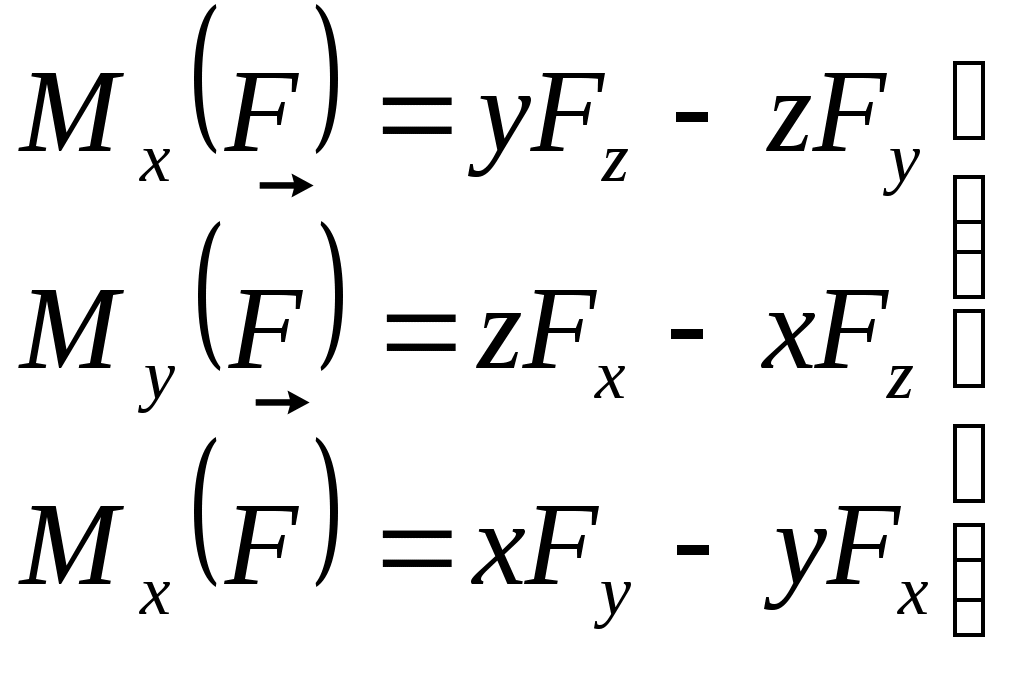 (70)
(70)
 ешение. Рассмотрим равновесие пластины ABCD. На нее действует только одна активная сила
ешение. Рассмотрим равновесие пластины ABCD. На нее действует только одна активная сила ешение. Найдем
ешение. Найдем  тносительно оси Ох. (-5)
тносительно оси Ох. (-5)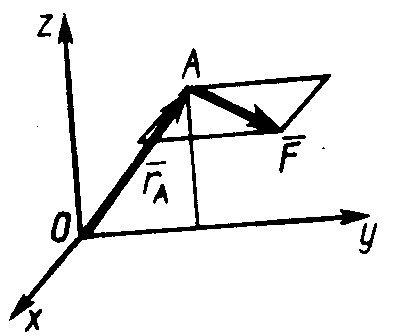



 .4.4. Момент силы
.4.4. Момент силы  .4.5. Момент силы
.4.5. Момент силы 


 .4.9. Квадратная пластина ABCD (рис. 316) весом G = 115 Н в горизонтальном положении закреплена шарнирно в трех вертикальных стержнях 1, 2 и 3. В точке А приложена вертикальная сила Q = 185 Н. Из уравнения равновесия моментов сил относительно оси BD определить усилие в стержне 2. (-185)
.4.9. Квадратная пластина ABCD (рис. 316) весом G = 115 Н в горизонтальном положении закреплена шарнирно в трех вертикальных стержнях 1, 2 и 3. В точке А приложена вертикальная сила Q = 185 Н. Из уравнения равновесия моментов сил относительно оси BD определить усилие в стержне 2. (-185)  .4.13.
.4.13.
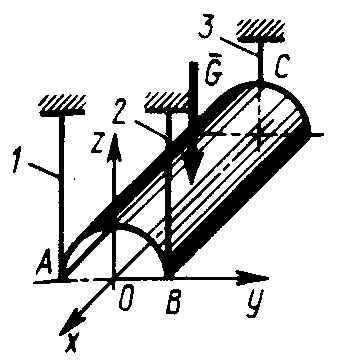

 .4.15. На трех вертикальных стержнях 1, 2 и 3 шарнирно закреплена горизонтальная прямоугольная платформа 4 с размерами ОА = 1,5 АВ и весом G = 1 кН (рис. 322). В точке Dна платформу давит пружина 5 с силой Q = 0,5 кН. Определить в кН реакцию в стержне 2. (0,5)
.4.15. На трех вертикальных стержнях 1, 2 и 3 шарнирно закреплена горизонтальная прямоугольная платформа 4 с размерами ОА = 1,5 АВ и весом G = 1 кН (рис. 322). В точке Dна платформу давит пружина 5 с силой Q = 0,5 кН. Определить в кН реакцию в стержне 2. (0,5) 




 .4.22. К валу. ОА под прямым углом прикреплены стержни ВС и DE(рис. 328). К стержню DE приложена распределенная нагрузка q= 0,5 Н/м. Определить модуль силы, уравновешивающей данную нагрузку, если
.4.22. К валу. ОА под прямым углом прикреплены стержни ВС и DE(рис. 328). К стержню DE приложена распределенная нагрузка q= 0,5 Н/м. Определить модуль силы, уравновешивающей данную нагрузку, если 




 .4.28. Однородная пирамида OABCD весом G = 60 Н (рис. 334) под действием пары сил с моментом М = 150 Н·м и наложенных связей находится в равновесии. Определить составляющую реакции шарнира В, параллельную оси Ох, если размер а = 3 м, а пара сил лежит в плоскости Оху. (50)
.4.28. Однородная пирамида OABCD весом G = 60 Н (рис. 334) под действием пары сил с моментом М = 150 Н·м и наложенных связей находится в равновесии. Определить составляющую реакции шарнира В, параллельную оси Ох, если размер а = 3 м, а пара сил лежит в плоскости Оху. (50) 
