Статика7. 2. статика в статике изучаются условия равновесия твердых тел под действием сил

• Название: 2. статика в статике изучаются условия равновесия твердых тел под действием сил
• Дата: 06.04.2021
• Размер: 1.32 Mb.
• Имя файла: Статика7.doc
• Тип: Документы; #191778
• страница: 3 из 9

Рис. 186 Рис. 187 Рис. 188

2.1.19. Груз удерживается в равновесии двумя стержнями АС и ВС, шарнирно соединенными в точках А, В и С (рис.188). Стержень ВС растянут силой F₂ = 45 Н, а стержень АС сжат силой F₁ = 17 Н. Определить вес груза, если заданы углы α =15° и β = 60°. (18,1)

2 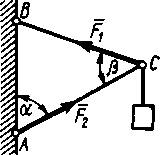.1.20. Шарнирный трехзвенник ABC (рис.189) удерживает в равновесии груз, подвешенный к шарнирно­му болту С. Под действием груза стержень АС сжат силой F₂ = 25 Н. Заданы углы α = 60° и β = 45°. Считая стержни АС и ВСневесомыми, определить усилие в

Рис. 189 стержне ВС. (48,3)

2.1.2. Момент силы относительно точки. Момент пары сил

2.1.21. Определить момент силы относительно начала координат, если сила задана проекциями F_х = F_y = 210 Н и известны координаты точки приложения силы

х = у = 0, 1 м.(0)

2.1.22. К вершине А квадратной пластины (рис.190), длины сторон которой равны 0,2 м, приложена сила F = 150 Н. Определить момент этой силы отно­сительно точки В. (-21,2)

2.1.23. Сила F = 420 Н, приложенная к точке А,лежит в плоскости Оху (рис.191). Определить момент силы относительно точки О, если координаты х_А = 0,2 м, у_А = 0,3 м и угол α = 30°. (151)

2.1.24 . На зубчатое колесо действует пара сил (рис. 192). Оп­ределить момент этой пары, если силы F = F' = 100 Н действуют на точки А и В, распо­ложенные на окружности радиуса r = 0,04 м, и образуют угол а = 20° с касательными к этой окружности. (7,52)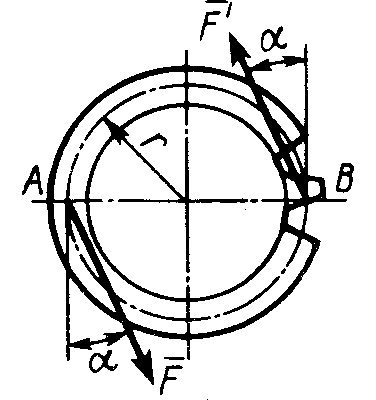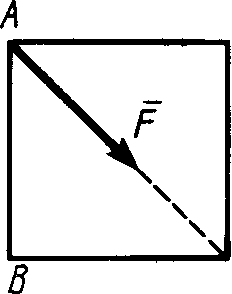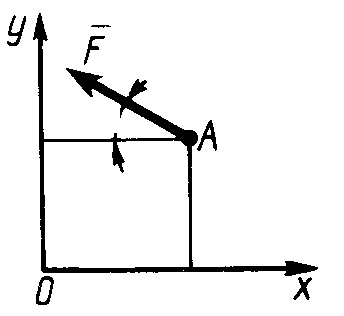







Рис. 190 Рис. 191 Рис. 192

2.1.25. Определить момент пары сил ( ), если силы (рис. 193) заданы проекциями F_x= - = 7,5 Н, F_y= - , = 2,5 Н и даны координаты точек приложения сил х₁ = 0,1 м, у₁ = 0,15, х₂= 0,015 м, у₂ = 0,02 м. (-0,762)

2.1.26. На плиту в ее плоскости действуют две пары сил (рис. 194).Определить сумму моментов этих пар, если сила F = 8 Н, Q = 5 Н, расстояния АВ = 0,25 м, CD = 0,20 м, углы α = 60°, β = 70°. (0,792)

2.1.27. На арку АВС (рис.195) действуют пара сил ( 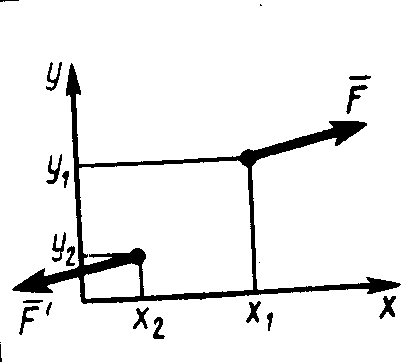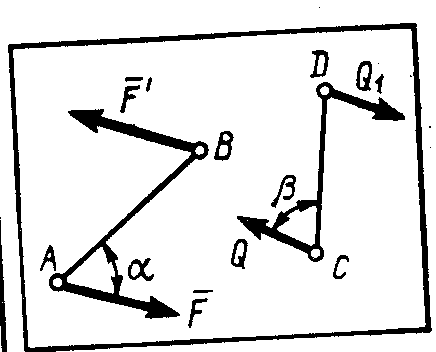) и сила F = 2 Н. Определить сумму их момен­тов относительно точки В, если сила F₁=3 Н, радиус r =1 м, плечо DE = 1,2 м, угол α = 45°. (5,01)


Рис. 193 Рис. 194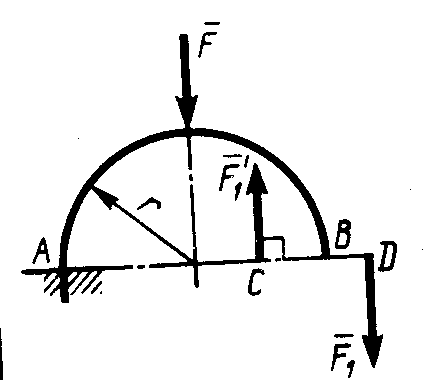

2.1.28. На арку АВ (рис.196) действуют пара сил ( ) и сила . Определить сумму их моментов отно­сительно точки А, если силы F= 4 Н, F₁= 2 Н, радиус r = 2 м, плечо CD = 1,5 м. (-11,0)


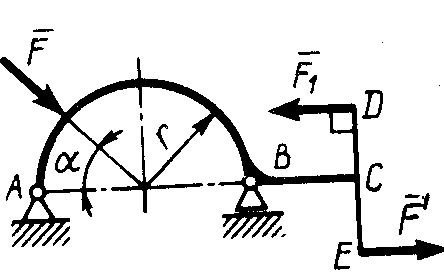Рис. 195 Рис. 196

2 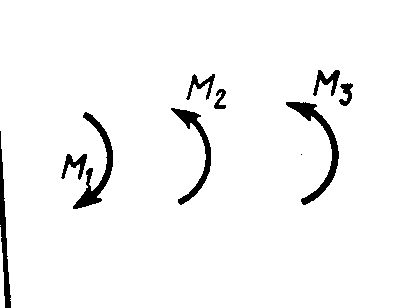.1.29. В одной плоскости расположены три пары сил (рис. 197). Определить момент пары сил М₃, при ко­тором эта система находится в равновесии, если моменты

Рис. 197 M₁ = 510 Н · м, М₂ = 120 Н · м. (390)

2.1.3. Система параллельных сил и произвольная плоская система сил

Уравнения равновесия твердого тела под действием произвольной плоской системы сил можно записать в од­ной из следующих форм: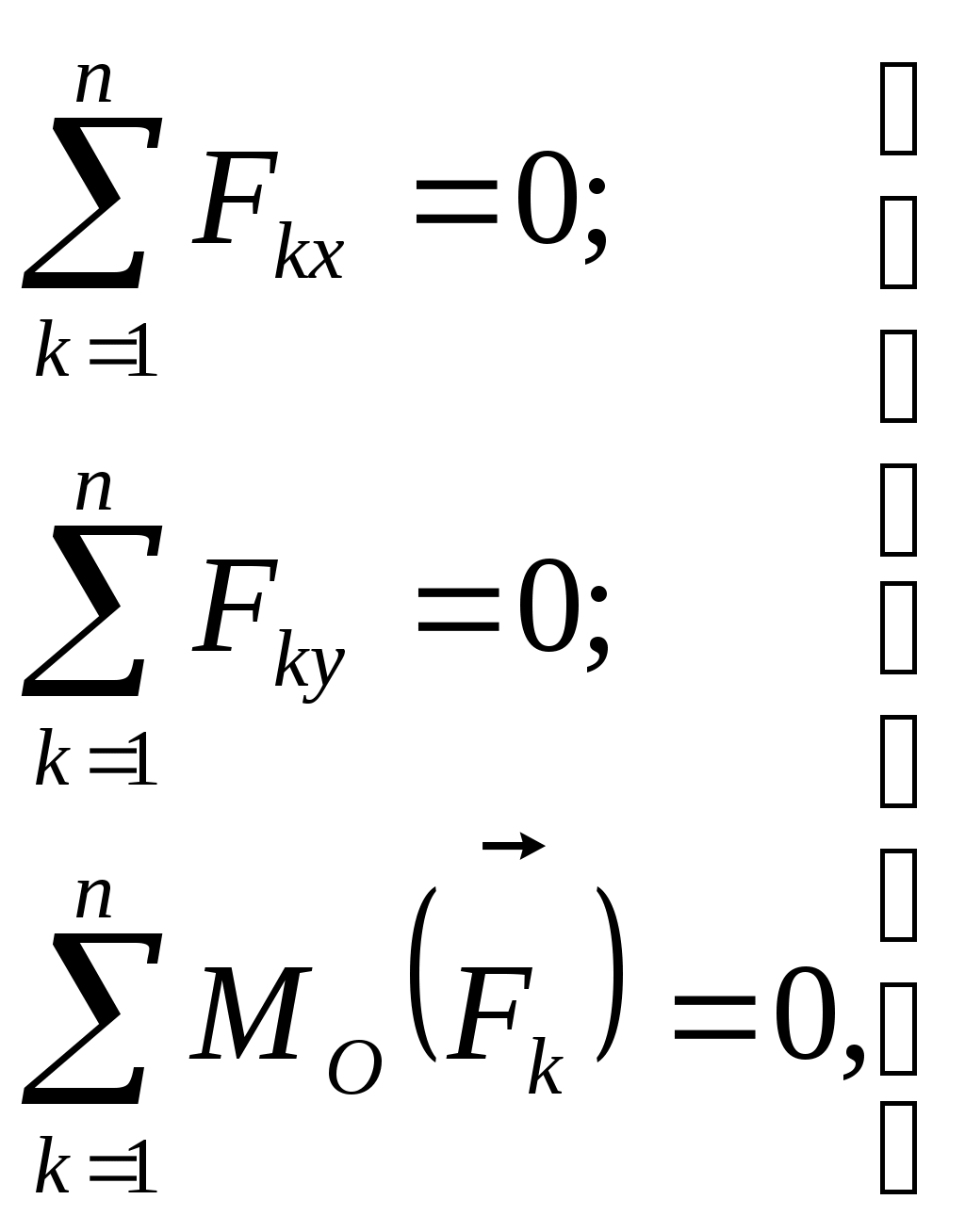

(59)

причем за центр моментов О принимают любую точку на плоскости;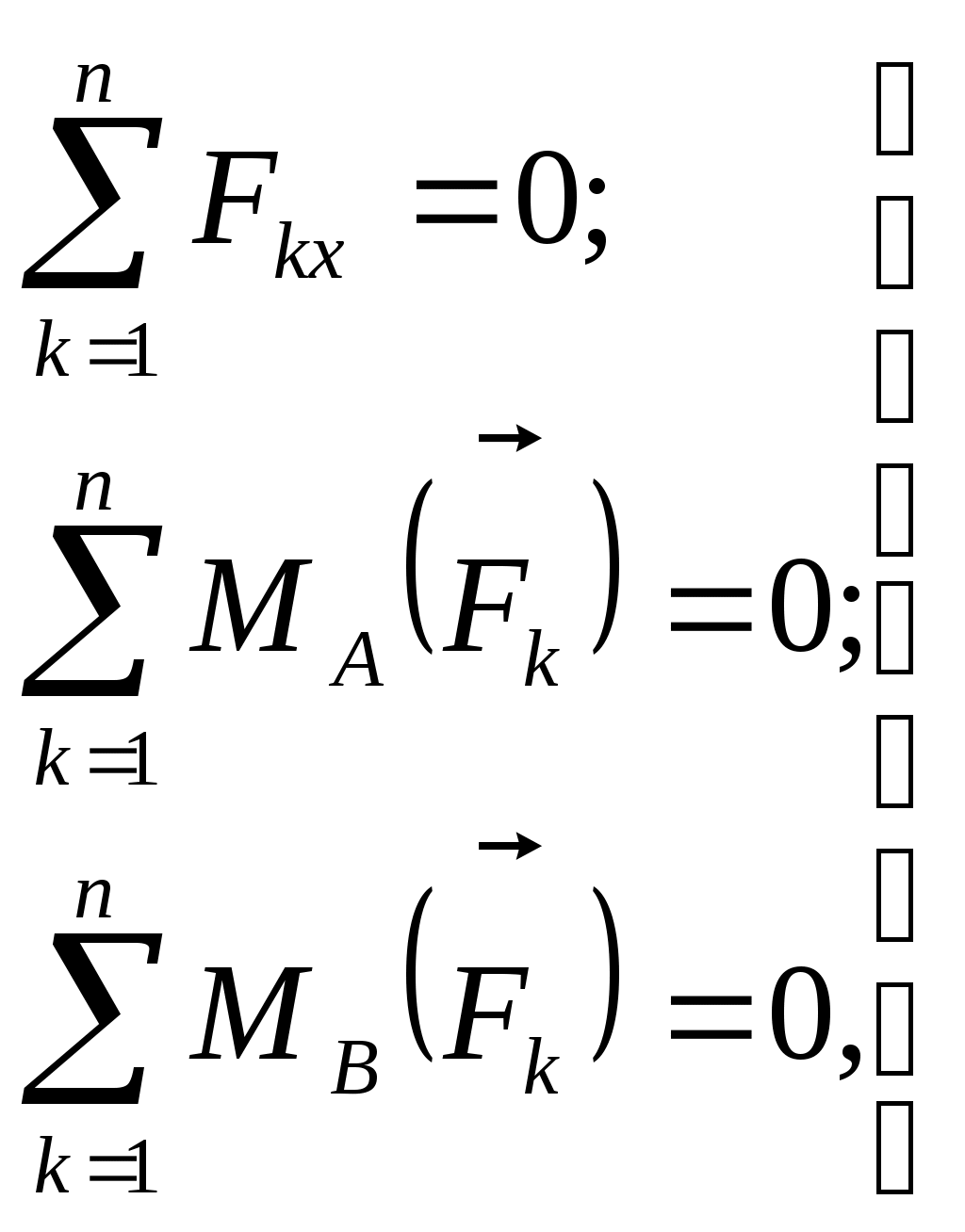

(60)

при этом прямая АВ, соединяющая центры моментов А и В, не должна быть перпендикулярной оси проекций х: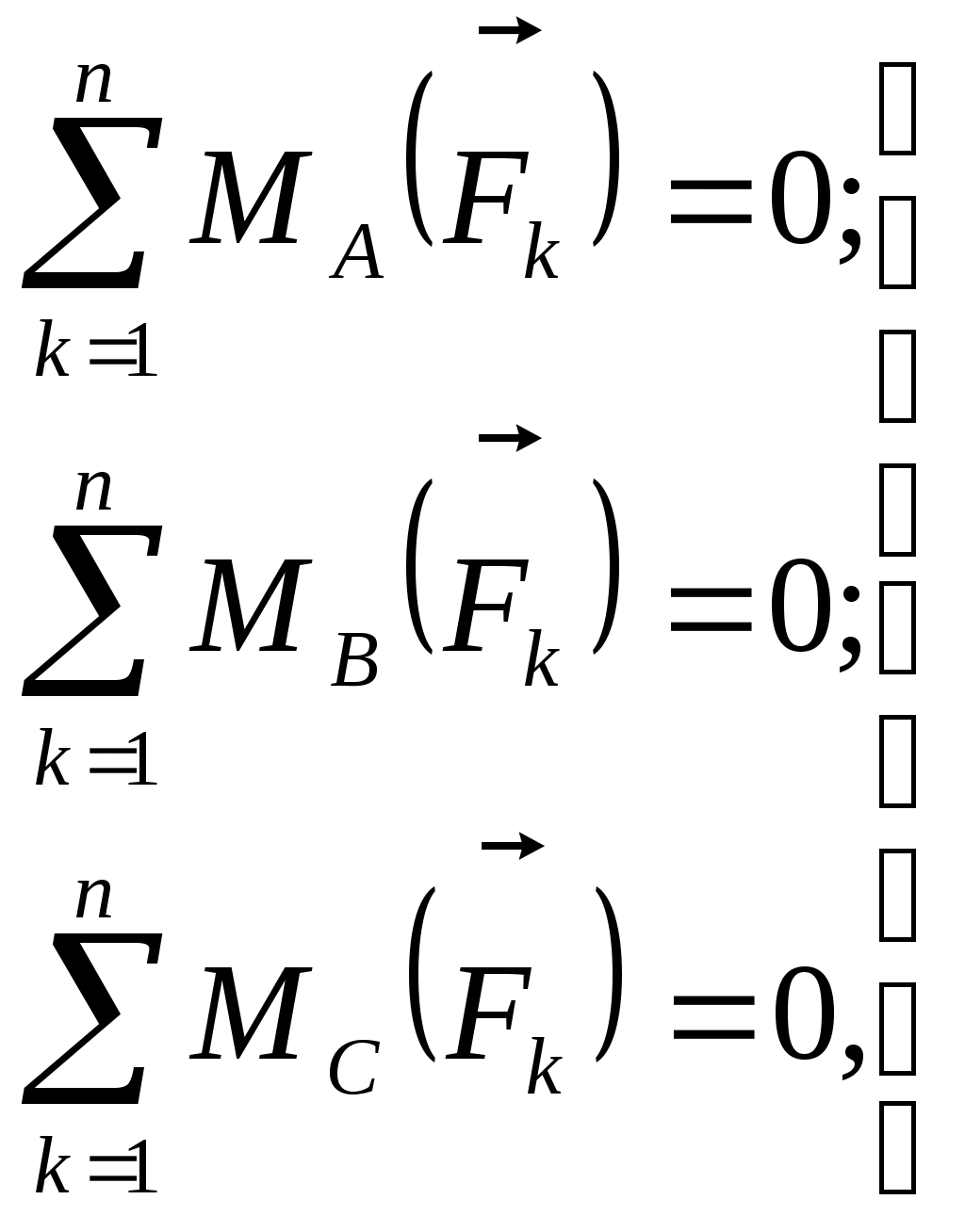

(61)

при этом центры моментов А, В, С не должны лежать на одной прямой.

Если все силы, расположенные в плоскости, взаимно параллельны, то число уравнений равновесия сократится до двух. Эти уравнения можно записать в одной из двух форм: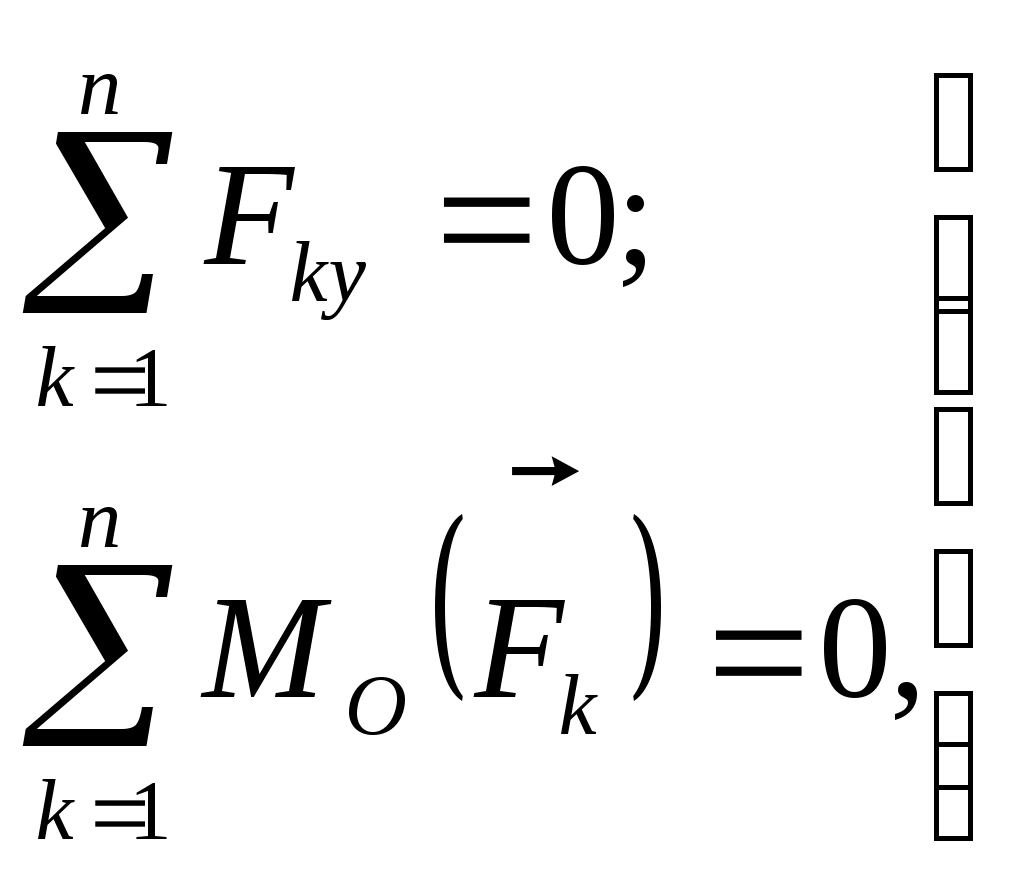

(62)

где ось у параллельна силам: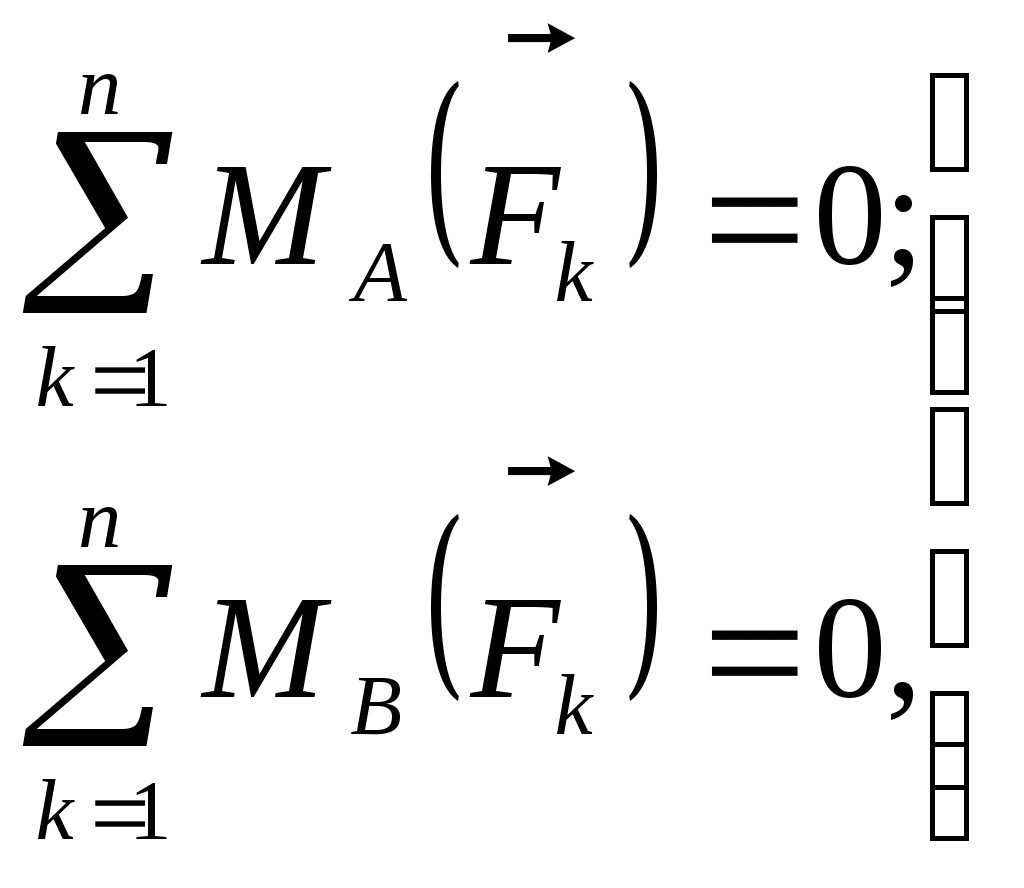

(63)

при этом отрезок АВ, соединяющий центры моментов А и В, не должен быть параллелен силам.

Для получения наиболее простых уравнений равнове­сия (если это не усложняет ход решения в остальном) следует одну из координатных осей проводить перпенди­кулярно возможно большему числу неизвестных сил, а за центр моментов брать точку, в которой пересекается возможно большее число неизвестных сил.

При вычислении момента силы удобно иногда разла­гать данную силу на составляющие и пользоваться тео­ремой о моменте равнодействующей (теоремой Вариньона).

Если на тело наряду с силами действуют и пары, ле­жащие в плоскости сил, то при составлении уравнений равновесия в уравнения проекций пары не войдут, так как сумма проекций сил пары на любую ось равна нулю. В уравнениях же моментов к моментам сил алгебраически прибавятся моменты пар, так как сумма моментов сил пары относительно любого центра равна моменту пары. При решении некоторых задач следует учитывать тре­ние скольжения или качения. Сила трения скольжения определяется по формуле

F_тр = fN, (64)

наибольшее значение момента трения каче­ния определяется по формуле

M = δN, (65)

где f – коэффициент трения скольжения,

δ - коэффициент трения качения в см;

N - модуль нор­мального давления.