Вопросы к экзамену Полесский. 29. Тесты гетероскедастичнсоти. 46
 Скачать 5.25 Mb. Скачать 5.25 Mb.
|
Понятие прогнозирования и его особенностиПрогнозирование – это вид познавательной деятельности человека, направленной на формирование прогнозов развития объектов, на основе анализа тенденций и закономерностей его развития. Прогнозирование – это научное, основанное на системе установленных причинно-следственных связей и закономерностей, выявление состояния и вероятностных путей развития явлений и процессов. Целью построения регрессионной функции на основе эмпирических данных является не только аппроксимация исходных данных с хорошей точностью, но и возможность дальнейшего применения полученного уравнения в экономических расчетах. В частности, на основе регрессионной модели можно вычислить прогнозное значение результативного признака при любых заданных значениях факторов. Под прогнозированием в эконометрике понимается построение оценки В прогнозных расчетах по уравнению регрессии определяется предсказываемое значение Так для линейной регрессии Точечный прогноз дополняется расчетом стандартной ошибки Поставим в уравнение регрессии выражение параметра Отсюда вытекает, что стандартная ошибка Соотношение (2) вытекает из свойств дисперсии: дисперсия групповой средней равна сумме дисперсий двух независимых слагаемых выражения (1). Учтено также, что Дисперсия выборочной средней 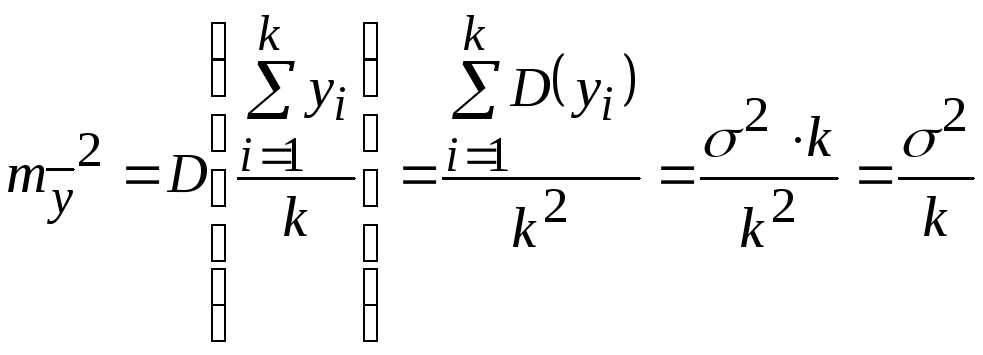 . .Для нахождения дисперсии 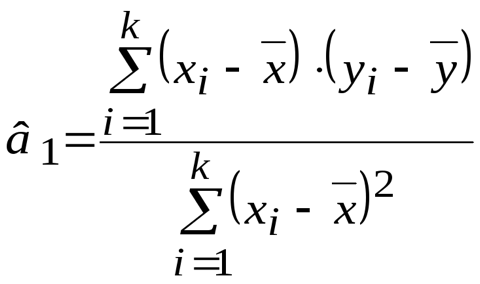 . Тогда . Тогда (вывод смотри ранее в разделе проверка качества уравнения регрессии). (вывод смотри ранее в разделе проверка качества уравнения регрессии).Используем в качестве оценки 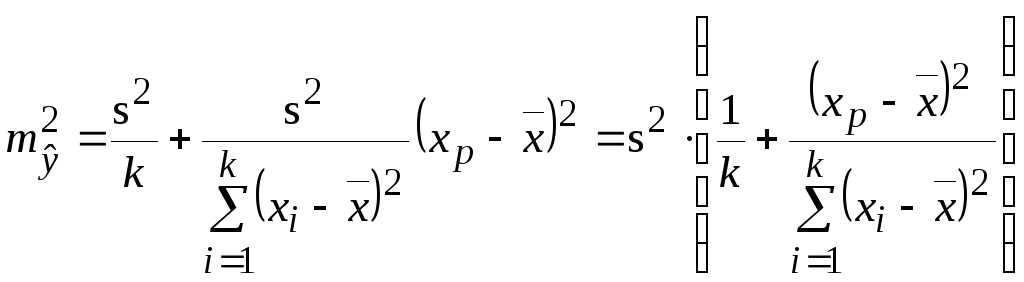 . (3) . (3)Основываясь на предпосылках регрессионного анализа, можно показать, что статистика  имеетt–распределение Стьюдента с ( имеетt–распределение Стьюдента с (где Таким образом, мы построим доверительный интервал для функции регрессии, то есть для математического ожидания. Он с заданной надежностью Прогноз значений зависимой переменной у по уравнению регрессии оправдан, если значение х объясняющей переменной не выходит за диапазон ее значений по выборке. Другими словами, экстраполяция кривой регрессии, то есть ее использование вне пределов обследованного диапазона значений объясняющей переменной может привести к значительным погрешностям. Рассмотренная формула (3) показывает, что величина Построенный доверительный интервал определяет местоположение модельной линии регрессии (среднего значения), но не отдельных возможных значений зависимой переменной, которые отклоняются от средней. Поэтому при определении доверительного интервала для индивидуальных значений Средняя ошибка прогнозируемого индивидуального значения  . (5) . (5) Соответствующий доверительный интервал для прогнозов индивидуальных значений будет определяться по формуле: где |
