Вопросы к экзамену Полесский. 29. Тесты гетероскедастичнсоти. 46

• Название: 29. Тесты гетероскедастичнсоти. 46
• Анкор: Вопросы к экзамену Полесский
• Дата: 12.03.2023
• Размер: 5.25 Mb.
• Имя файла: Voprosy_k_ekzamenu_po_distsipline_Ekonometrika_1.doc
• Тип: Документы; #982220
• страница: 12 из 34

Анализ структурных изменений.

Как отмечено в гл. 6, значения временного ряда формируются под действием большого числа различных показателей. Кроме факторов, определяющих долгосрочные тенденции, циклические и сезонные колебания, на динамику изучаемого признака могут оказывать влияние единовременное качественное изменение экономической ситуации, которое обычно вызвано событиями глобального характера (экономические кризисы и реформы, войны, стихийные бедствия и т.п.), а также переменой рыночной ситуации. В этих случаях говорят, что наблюдаются структурные изменения в динамике временного ряда. Их последствия заключаются в том, что, начиная с некоторого момента времени t*, меняется характер динамики временного ряда. Поэтому может быть целесообразно построение двух отдельных моделей, описывающих динамику изучаемого показателя до момента времени t* и после него. Следует отметить, что по типу воздействия на значения временного ряда структурные изменения могут быть разделены на две группы — структурные изменения мгновенного действия (землетрясения, резкие изменения котировок акций и различных экономических индексов вследствие банкротства крупных международных корпораций и др.) и проявляющиеся в процессе развития экономической ситуации (различные инфляционные и дефляционные процессы).

Пример. На рис. 7.2 представлены подобные изменения в динамике продаж одного из новосибирских супермаркетов [77], вызванные открытием в июле в микрорайоне, где он расположен, магазина-конкурента, работающего в аналогичном формате.

Основная цель анализа структурных изменений во временных рядах заключается в обосновании выбора между единой (общей) моделью, построенной на всем рассматриваемом промежутке времени, и кусочной моделью, составленной из двух отдельных моделей, построенных на промежутках времени до и после t*. Каждая из представленных моделей обладает своими характерными особенностями. Очевидным преимуществом кусочной модели является ее большая гибкость, позволяющая точнее описывать исходные данные. Это приводит к тому, что, как правило, остаточная сумма квадратов кусочной модели заметно ниже остаточной суммы квадратов единой модели. Однако разделение исходных данных на две группы влечет за собой существенное снижение степеней свободы для каждой составляющей кусочной модели и, следовательно, приводит к потере части информации, содержащейся в исходных данных.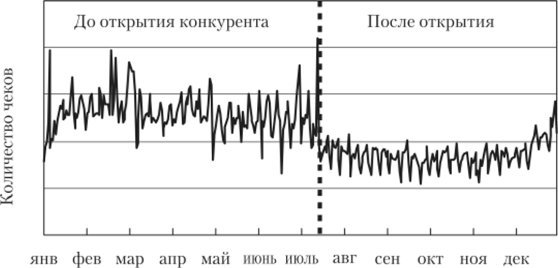



Выбор между единой и кусочной моделью должен основываться на анализе соотношения между снижением остаточной суммы квадратов и потерей числа степеней свободы. Для статистического обоснования этого выбора разработан ряд специальных критериев [2, 3, 281. Рассмотрим некоторые из них, для простоты изложения предполагая, что временной ряд не подвержен влиянию сезонных и циклических воздействий или их последствия каким-либо образом оценены, а соответствующие компоненты исключены из временного ряда.

8. Тест структурных изменений.

Исходные данные, которые не обладают определенностью, т.е. имеется излом тенденции, можно моделировать с помощью следующих способов:

1. Разделить имеющиеся данные на однородные участки и рассмотреть каждый участок в отдельности, Применяется, когда излом тенденции значительный, а выборка позволяет разбить ее на 2 подвыборки (выборка должна быть большая).

2. Построить единую модель по всем данным. Используется, если излом тенденции несущественен и объем выборки не позволяет разбить ее на 2 части.

3. Ввести в модель фиктивные переменные, т.е. получить кусочно-линейные регрессионные модели, которые позволяют, с одной стороны, не разбивать исходную выборку, с другой – улучшить качество подгонки уравнений.

Формальный критерий выбора между моделями раздельными и объединенной – критерий Чоу.

Схема теста Чоу:

Пусть P – общая выборка, A, B – под выборки

Уравнения	yp=ap+b1px1p+…+bkp (k-факторов)	yA=aA+b1Ax1+…+bkAA (kA-факторов)	YB=aB+b1Bx1+…+bkBB(kB-факторов)
Число наблюдений	n(nA+nB-n)	nA	nB
Сумма квадратов остатков
Число степеней свободы	n-k	nA-kA	nB-kB
Сумма квадратов остатков в общей регрессии для наблюдений, относящихся к подвыборкам	E=EAp+EBp	EAp	EBp

После определения всех показателей таблицы рассматривается F-статистика

Определяется F_табл со степенями свободы V₁=(k_A+k_B-k), V₂=(n-k_A-k_b).

Если F_расчтабл, то делается вывод, что лучше оценивать объединенную модель.

Кроме сезонных и циклических колебаний весьма важную роль играют единовременные изменения характера тенденции временного ряда. Эти (относительно) быстрые однократные изменения тренда (его характера) вызываются структурными изменениями в экономике либо мощными глобальными (внешними) факторами. Прежде всего выясняется, значимо ли повлияли общие структурные изменения на характер тренда. При условии значимости такого влияния (структурных изменений) на характер тренда используется кусочно-линейная модель регрессии. Кусочно-линейная модель означает представление исходной совокупности данных ряда в виде двух частей. Одна часть данных моделируется просто линейной моделью с одним коэффициентом регрессии (углом наклона прямой) и представляет данные до момента (периода) структурных изменений. Вторая часть данных — это тоже линейная модель, но уже с иным коэффициентом регрессии (углом наклона).

После построения двух таких моделей (подмоделей) линейной регрессии получают уравнения двух соответствующих прямых. Если структурные изменения незначительно повлияли на характер тенденции ряда, то вместо построения точной кусочно-линейной модели вполне можно использовать единую аппроксимирующую модель, т.е. одну общую линейную зависимость (одну прямую), тоже вполне приемлемо представляющую данные в целом. Незначительное ухудшение в отдельных данных при этом непринципиально.

Если строится кусочно-линейная модель, то снижается остаточная сумма квадратов по сравнению с единым для всей совокупности уравнением тренда. В то же время разделение исходной совокупности на две части ведет к потере числа наблюдений и тем самым к снижению числа степеней свободы в каждом уравнении кусочно-линейной модели. Единое уравнение для всей совокупности данных позволяет сохранить число наблюдений исходной совокупности. Остаточная сумма квадратов по этому уравнению в то же время выше, чем такая же сумма для кусочно-линейной модели. Выбор конкретной — кусочно-линейной или просто линейной — модели, т.е. единого уравнения тренда, зависит от соотношения между снижением остаточной дисперсии и потерей числа степеней свободы при переходе от единого уравнения регрессии к кусочно-линейной модели.

Для оценки этого соотношения был предложен статистический тест Грегори — Чоу. В этом тесте рассчитываются параметры уравнений трендов, вводится гипотеза о структурной стабильности тенденции исследуемого ряда динамики. Ясно, что остаточную сумму квадратов кусочно-линейной модели можно найти как сумму соответствующих сумм квадратов для обеих линейных компонент модели. Сумма числа степеней свободы этих компонент дает число степеней свободы всей модели в целом. Тогда сокращение остаточной дисперсии при переходе от единого уравнения тренда к кусочно-линейной модели — это просто остаточная сумма квадратов, из которой вычтены соответствующие суммы для обеих компонент кусочно-линейной модели. Столь же просто определяется и соответствующее число степеней свободы.

После этого рассчитывается фактическое значение F-критерия по дисперсиям на одну степень свободы. Это значение сравнивают с табличным, полученным по таблицам распределения Фишера для требуемого уровня значимости и соответствующего числа степеней свободы. Как всегда, если расчетное (фактическое) значение больше табличного (критического), то гипотеза о структурной стабильности (незначимости структурных изменений) отклоняется. Влияние же структурных изменений на динамику изучаемого показателя признается значимым. Таким образом, следует моделировать тенденцию ряда динамики с помощью кусочно-линейной модели. Если же расчетное значение меньше критического, то нельзя отклонять нуль-гипотезу без риска сделать неверный вывод. В этом случае следует использовать единое для всей совокупности уравнение регрессии как наиболее достоверное и минимизирующее вероятность ошибки.