Вопросы к экзамену Полесский. 29. Тесты гетероскедастичнсоти. 46

• Название: 29. Тесты гетероскедастичнсоти. 46
• Анкор: Вопросы к экзамену Полесский
• Дата: 12.03.2023
• Размер: 5.25 Mb.
• Имя файла: Voprosy_k_ekzamenu_po_distsipline_Ekonometrika_1.doc
• Тип: Документы; #982220
• страница: 15 из 34

Тест Голдфельда – Квандта.

В тесте Голдфелда-Квандта используется предположение о прямой зависимости дисперсии ошибки (остатка) от величины некоторой независимой переменной. Схема применения этого теста такова. Сначала данные упорядочиваются по убыванию той независимой переменной, относительно которой имеется подозрение на гетероскедастичность. Затем в этом упорядоченном наборе данных исключают несколько средних наблюдений, где несколько означает примерно четверть от общего количества наблюдений.

Далее проводятся две независимые регрессии для первых из оставшихся (после выполненного исключения) средних наблюдений и двух последних из этих оставшихся средних наблюдений. После этого строятся два соответствующих остатка. Наконец, составляется F-статистика Фишера и, если верна исследуемая гипотеза, то F действительно является распределением Фишера с соответствующими степенями свободы. Тогда большая величина этой статистики означает, что проверяемую гипотезу необходимо отвергнуть. Без шага исключения наблюдений мощность данного теста уменьшается.

Алгоритм: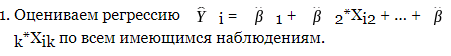

2. 
   Строим и анализируем график остатков. Может появиться предположение о том, что дисперсия возмущений увеличивается с некоторой переменной - Xj.
   
3. 
   Упорядочиваем все наблюдения по модулю переменной Xj, начиная с ее наименьшего значения и заканчивая наибольшим.
   
4. 
   Выкидываем m центральных переменных, а по первым n1 и по последним n2 наблюдениям оцениваем регрессию из (1). Обычно, если количество наблюдений велико, то m=n1=n2.
   
5. 
   Для регрессий по n1 и n2 наблюдениям получаем, соответственно, RSS1 и RSS2.
   

6. Составляем F-статистику:



7. Если Fn1-k,n2-k>Fкрит, то гипотеза о гомоскедастичности отвергается, следовательно, в модели присутствует гетероскедастичность.

8. Тест Уайта. Метод Глейзера.

Пусть имеется линейная регрессия:



Необходимо проверить гетероскедастичность случайных ошибок модели  . Тест использует остатки регрессии, оценённой с помощью обычного метода наименьших квадратов. Для теста оценивается (также обычным МНК) вспомогательная регрессия квадратов этих остатков на все регрессоры (включая константу, даже если её не было в исходной модели), их квадраты и попарные произведения:



 — остатки регрессии;

 — факторы исходной регрессии;

 — параметры вспомогательной регрессии — соответственно константа, вектор линейных коэффициентов и матрица коэффициентов при квадратах и попарных произведениях факторов.

-случайная ошибка вспомогательной модели.

В данной записи без ограничения общности матрицу   можно считать треугольной. В другом варианте теста в модель не включаются попарные произведения, тогда матрица   - диагональная.

В тесте проверяется нулевая гипотеза об отсутствии гетероскедастичности (то есть ошибки модели предполагаются гомоскедастичными — с постоянной дисперсией). В таком случае вспомогательная регрессия должна быть незначимой. Для проверки этой гипотезы используется LM-статистика  , где   — коэффициент детерминации вспомогательной регрессии,  -количество наблюдений. При отсутствии гетероскедастичности данная статистика имеет асимптотическое распределение  , где   - количество параметров вспомогательной регрессии. Следовательно, если значение статистики больше критического значения этого распределения для заданного уровня значимости, то нулевая гипотеза отвергается, то есть имеется гетероскедастичность. В противном случае гетероскедастичность признается незначимой (случайные ошибки скорее всего гомоскедастичны).

Метод Глейзера.

С помощью обычного МНК оценивается исходная регрессионная модель



и находятся остатки регрессии  .

Далее для различных значений   (обычно начинают с  ) оценивается (также с помощью обычного МНК) вспомогательная регрессия:



Для каждого значения   проверяется статистическая значимость коэффициента   с помощью стандартного критерия Стьюдента или эквивалентного ему в данном случае F-теста на значимость вспомогательной регрессии в целом. Если для некоторых   коэффициент   признается значимым (тестовая статистика больше критического значения), то гетероскедастичность данного вида признается значимой и выбирается модель с тем значением  , для которого коэффициент   наиболее значим (с наибольшим значением тестовой статистики).