Вопросы к экзамену Полесский. 29. Тесты гетероскедастичнсоти. 46
 Скачать 5.25 Mb. Скачать 5.25 Mb.
|
Гетероскедастичность: суть, причины, последствия.Гетероскедастичность— понятие, означающее неоднородность наблюдений, выражающуюся в неодинаковой (непостоянной) дисперсии случайной ошибки регрессионной (эконометрической) модели. Гетероскедастичность противоположна гомоскедастичности, означающей однородность наблюдений, то есть постоянство дисперсии случайных ошибок модели. Причины: в пространств выборках при зависимости масштаба измерений зависимой переменной от некоторой переменной, называемой фактором пропорциональности во врем рядах, когда зависимая переменная имеет большой интервал качественно неоднородных значений или высокий темп изменений в любой модели – если качество данных варьируется внутри выборки. Наличие гетероскедастичности случайных ошибок приводит к неэффективности оценок, полученных с помощью метода наименьших квадратов. Кроме того, в этом случае оказывается смещённой и несостоятельной классическая оценка ковариационной матрицы МНК-оценок параметров. Следовательно, статистические выводы о качестве полученных оценок могут быть неадекватными. В связи с этим тестирование моделей на гетероскедастичность является одной из необходимых процедур при построении регрессионных моделей. Методы анализа гетероскедастичнсоти ошибки.Наличие гетероскедастичности можно проверить визуально на основе графиков остатка. Для этого нужно провести построение уравнения регрессии с выводом графика остатка. О наличии гетероскедастичности свидетельствует величина разброса остатков относительно оси абсцисс. Если разброс примерно одинаков, то можно считать, что выполняется условие гомоскедастичности, если же разброс увеличивается/уменьшается с ростом какого-либо из факторов, то остатки скорее всего гетероскедастичны. Для получения информации об адекватности построенной модели многомерной линейной регрессии исследуют регрессионные остатки. Если выбранная регрессионная модель хорошо описывает истинную зависимость, то остатки должны быть независимыми нормально распределенными случайными величинами с нулевым средним, и в их значениях должен отсутствовать тренд. Анализ регрессионных остатков — это процесс проверки выполнения этих условий. Пример проверки см. в статье «Анализ регрессионных остатков (пример)». Для того, чтобы регрессионная модель хорошо описывала истинные данные, регрессионные остатки должны обладать следующими свойствами: (1) Эту гипотезу можно проверять любым параметрическим или непараметрическим критерием сравнения среднего с заданным значением ( в данном случае - с нулём). - т.е. одинаковая дисперсия. Проверяется аналогично, любым параметрическим или непараметрическим критерием сравнения дисперсии с заданным значением. Например, Критерий Зигеля-Тьюки. Это дополнительное предположение. Его важно проверить, если для проверки других свойств регрессионных остатков мы хотим использовать статистический критерий, предполагающий нормальность данных. Для проверки этой гипотезы можно использовать Критерий нормальности. (4) - независимы. Тесты гетероскедастичнсоти.Явление гетероскедастичности возникает, как правило, при анализе неоднородных объектов. Например, при построении зависимости прибыли фирмы от размера основного фонда (или каких-либо других факторов) гетероскедастичность вызвана тем, что у больших фирм колебания прибыли будут выше, чем у малых. МНК при наличии гетероскедастичности позволяет получить несмещенные оценки параметров модели, но оценка дисперсии ошибки, и, следовательно, границы доверительных интервалов оценок параметров модели и прогноза зависимой переменной будут неверными, т.к. они вычисляются на основании предположения гомоскедастичности ошибок. Для проверки на гетероскедастичность существует большое число тестов. Наиболее популярные: тест Голдфельда-Квандта и тест Уайта. Тест Голдфельда-Квандта 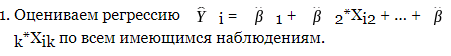 Строим и анализируем график остатков. Может появиться предположение о том, что дисперсия возмущений увеличивается с некоторой переменной - Xj. Упорядочиваем все наблюдения по модулю переменной Xj, начиная с ее наименьшего значения и заканчивая наибольшим. Выкидываем m центральных переменных, а по первым n1 и по последним n2 наблюдениям оцениваем регрессию из (1). Обычно, если количество наблюдений велико, то m=n1=n2. Для регрессий по n1 и n2 наблюдениям получаем, соответственно, RSS1 и RSS2. 6. Составляем F-статистику: 7. Если Fn1-k,n2-k>Fкрит, то гипотеза о гомоскедастичности отвергается, следовательно, в модели присутствует гетероскедастичность. Тест Глейзера Строим уравнение регрессии Для уравнения регрессии из (1) находим ряд остатков Оцениваем следующие модели: 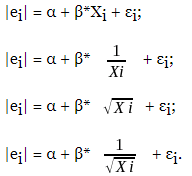 Для каждой из 4ех моделей тестируем значимость коэффициента β. 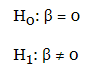 Если хотя бы в одной модели коэффициент β оказался значимым, то в модели присутствует гетероскедастичность. Если во всех моделях коэффициент β оказался незначимым, то имеет место гомоскедастичность. Тест Парка Строим уравнение регрессии Для уравнения регрессии из (1) находим ряд остатков Выбираем фактор пропорциональности и оцениваем вспомогательную регрессию Проверяем значимость α2. Если коэффициент значим, то в модели присутствует гетероскедастичность. |
