Вопросы к экзамену Полесский. 29. Тесты гетероскедастичнсоти. 46

• Название: 29. Тесты гетероскедастичнсоти. 46
• Анкор: Вопросы к экзамену Полесский
• Дата: 12.03.2023
• Размер: 5.25 Mb.
• Имя файла: Voprosy_k_ekzamenu_po_distsipline_Ekonometrika_1.doc
• Тип: Документы; #982220
• страница: 8 из 34

Анализ вариации зависимой переменной.

Цель регрессионного анализа состоит в объяснении поведения зависимой переменной y.

Пусть на основе выборочных наблюдений построено уравнение регрессии  , тогда значение зависимой переменной y в каждом наблюдении можно разложить на две составляющие: , где остаток ei есть та часть зависимой переменной y, которую невозможно объяснить с помощью уравнения регрессии.

Разброс наблюдаемых значений зависимой переменной характеризуется выборочной дисперсией var(y).

Разложим дисперсию var(y):



Поскольку   то



Таким образом, разложили дисперсию var(y) на две части:

 – часть, объясненную регрессионным уравнением;

 – необъясненную часть

8. Коэффициент детерминации модели.

Коэффициент детерминации отражает меру качества регрессионной модели, описывающей связь между зависимой и независимыми переменными модели. Коэффициент детерминации показывает, какая доля вариации объясняемой переменной y учтена в модели и обусловлена влиянием на нее факторов, включенных в модель:



где   – значения наблюдаемой переменной,   – среднее значение по наблюдаемым данным,   – модельные значения, построенные по оцененным параметрам.

В случае, когда значение константы задается вручную, коэффициент детерминации рассчитывается по следующей формуле:



где   – фиксированное значение константы. В случае линейной регрессии с константой справедлива следующая формула:



Заметим, что данная формула справедлива только для модели с константой, в общем случае используется предыдущая формула.

Чем ближе   к 1, тем выше качество модели.

При равенстве коэффициента единице линия регрессии точно соответствует всем наблюдениям.

Равенство коэффициента нулю означает, что выбранные факторы не улучшают качество предсказания   по сравнению с тривиальным предсказанием  .

Достаточно качественной можно признать модель с коэффициентом детерминации выше 0,8.

Недостатком коэффициента детерминации является то, что он увеличивается при добавлении новых объясняющих переменных, что необязательно означает улучшение качества регрессионной модели. По этой причине, для устранения этого недостатка, на практике чаще используется скорректированный коэффициент детерминации

8. Проверка гипотез о значимости коэффициентов регрессии и адекватности модели.

Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.

Основная гипотеза состоит в предположении о незначимости коэффициентов модели множественной регрессии, т. е.



Обратная - о значимости коэффициентов модели множественной регрессии, т. е.



Данные гипотезы проверяются с помощью t-критерия Стьюдента, который вычисляется посредством частного F-критерия Фишера-Снедекора.

При проверке основной гипотезы применяется зависимость, которая существует между t-критерием Стьюдента и частным F-критерием Фишера-Снедекора: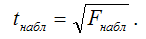



Значение t-критерия определяется как tкрит(а;n-l-1), где а – уровень значимости, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров, (n-l-1) – число степеней свободы, которое определяется по таблице распределений t-критерия Стьюдента.

При проверке основной гипотезы вида



наблюдаемое значение частного F-критерия Фишера-Снедекора рассчитывается по формуле:



При проверке основной гипотезы возможны следующие ситуации.

Если tнабл>=tкрит (tкрит берется из таблицы распределения Стьюдента), то основная гипотеза отвергается, и наблюдаемое значение является значимым.

Если tнабл k модели множественной регрессии принимается.

Наблюдаемое значение F-критерия (вычисленное на основе выборочных данных) сравнивают со значением Fкритическое, которое определяется по таблице распределения Фишера-Снедекора.

При проверке значимости коэффициента множественной корреляции, F критическое определяется как Fкрит(a;k1;k2), где а – уровень значимости, k1=l–1 и k2=n–l – число степеней свободы, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров.

При проверке основной гипотезы Fнаблюдаемое рассчитывается :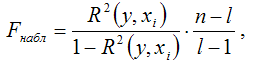



где R2(y,xi) – коэффициент множественный детерминации.
При проверке основной гипотезы возможны следующие ситуации.

Если наблюдаемое Fнабл>Fкрит, то с вероятностью а основная гипотеза отвергается, и признак признаётся значимым. Следовательно, модель множественной регрессии в целом также значима.

Если Fнабл<=Fкрит, то основная гипотеза принимается, и признак незначим. И модель - незначима.

Адекватность модели — совпадение свойств (функций/параметров/характеристик и т. п.) модели и соответствующих свойств моделируемого объекта. 

Оценка адекватности модели — проверка соответствия модели реальной системе. Оценка адекватности модели реальному объекту оценивается по близости результатов расчетов экспериментальным данным.

Два основных подхода к оценке адекватности:

1) по средним значениям откликов модели и системы

2) по дисперсиям отклонений откликов модели от среднего значения откликов систем