Вопросы к экзамену Полесский. 29. Тесты гетероскедастичнсоти. 46

• Название: 29. Тесты гетероскедастичнсоти. 46
• Анкор: Вопросы к экзамену Полесский
• Дата: 12.03.2023
• Размер: 5.25 Mb.
• Имя файла: Voprosy_k_ekzamenu_po_distsipline_Ekonometrika_1.doc
• Тип: Документы; #982220
• страница: 9 из 34

Доверительные интервалы. Ошибки спецификации модели.

//доверительные интервалы

Доверительным называется интервал, который с заданной надежностью альфа  покрывает оцениваемый параметр.

Для оценки математического ожидания   случайной величины  , распределенной по нормальному закону, при известном среднем квадратическом отклонении   служит доверительный интервал:


где 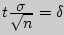  - точность оценки,

   - объем выборки, 

 - выборочное среднее, 

  - аргумент функции Лапласа, при котором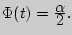 

Для нормального распределения существуют следующие соотношения между доверительными интервалами и доверительной вероятностью: 1s (Р=0,68), 2s (Р= 0,95), 3s (Р= 0,997), 4s (Р=0,999)

//ошибки спецификации

Возможные ошибки спецификации модели:

1. Неправильный выбор вида уравнения регрессии

2. В уравнение регрессии включена лишняя (незначимая) переменная

3. В уравнении регрессии пропущена значимая переменная

1. 
   Неправильный выбор вида функции в уравнении
   

Пусть на первом этапе была сделана спецификация модели в виде: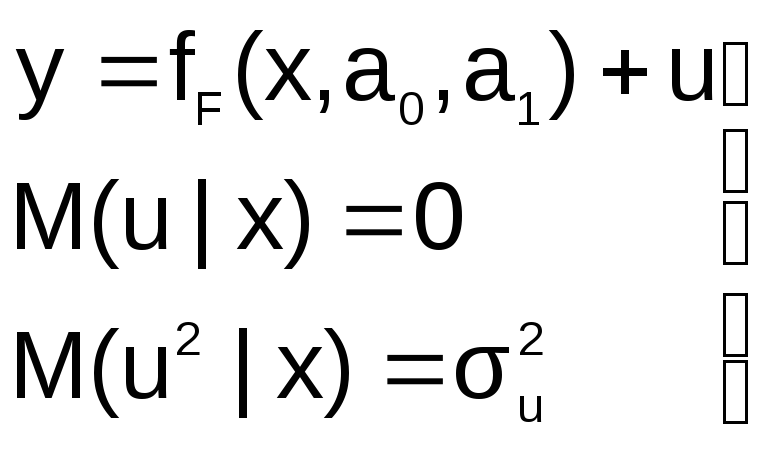




в которой функция f_F(x,a₀,a₁) выбрана не верно. Предположим, что y_T=f_T(x,a₀,a₁)+v – правильный вид функции регрессии.
Тогда справедливо выражение: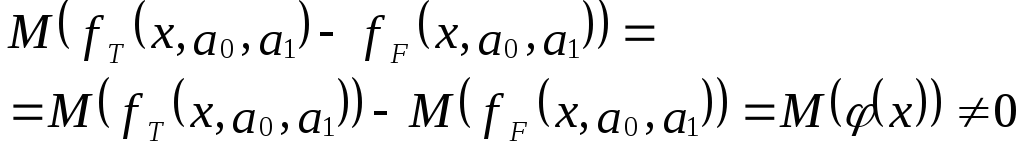

Из выражения следует:



Иными словами, математические ожидания эндогенной переменной, полученные с помощью функций f_T и f_F не совпадают, т.е. первая предпосылка теоремы Гаусса-Маркова M(ulx)=0 не выполняется

Следовательно, в результате оценивания такой модели параметры а₀ и а₁ будут смещенными

2. В уравнение регрессии включена лишняя переменная

Пусть на этапе спецификации в модель включена «лишняя» переменная, например, X₂



«Правильная» спецификация должна иметь вид: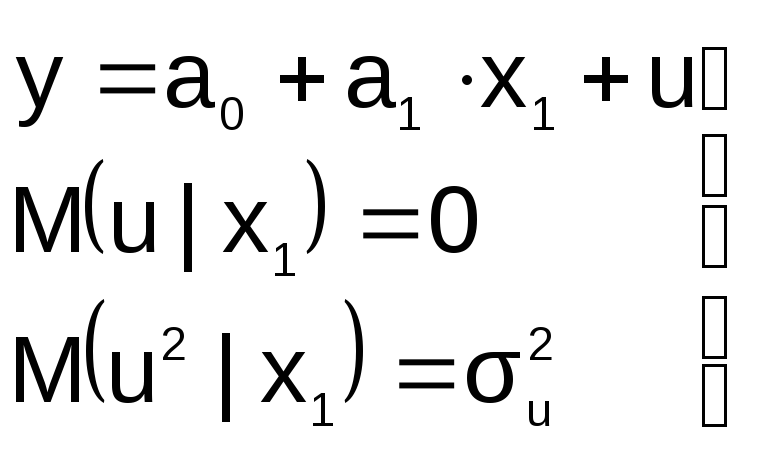







Последствия:

1. Оценки параметров а₀, а₁, а₂ останутся несмещенными, но потеряют свою эффективность (точность)

2. Увеличивается ошибка прогноза по модели

как за счет ошибок оценок коэффициентов и σ_u, так и за счет последнего слагаемого. Это особенно опасно при больших абсолютных значениях регрессора

3. В модели не достает важной переменной

Последствия такие же, как и в первом случае: получаем смещенные оценки параметров модели

Для устранения необходимо вернуться к изучению особенностей поведения экономического объекта, выявить опущенные переменные и дополнить ими модель

8. Прогнозирование в регрессионных моделях.

Регрессионные связи – связи между случайными и неслучайными величинами.

Регрессионный анализ – изучение регрессионных связей.

Математическая формулировка задачи регрессионного анализа

Требуется найти аналитическое выражение зависимости экономического явления (например, производительности труда) от определяющих его факторов, т.е. ищется функция следующего вида:

y=f(x₁, x₂, ... x_n);
Данная функция отражает зависимость, по которой можно найти приближенное значение зависимого показателя y. В качестве функции в регрессионном анализе принимается случайная переменная, а аргументами являются неслучайные переменные.

Примерами возможного применения регрессионного анализа в экономике являются исследование влияния на производительность труда и себестоимость таких факторов, как величина основных производственных фондов, заработная плата и др. Влияния безработицы на изменения заработной платы на рынках труда (кривые Филипса); зависимость структуры расходов от уровня доходов (кривые Энгеля); функции потребления и спроса и многие другие.

При выборе вида регрессионной зависимости руководствуются следующим: он должен согласовываться с профессионально-логическими соображениями относительно природы и характера и исследуемых связей; по возможности используют простые зависимости, не требующие сложных расчетов, легко экономически интерпретируемые и практически применимые.

Практика регрессионного анализа говорит о том, что уравнение линейной регрессии часто достаточно хорошо выражает зависимость между показателями даже тогда, когда на самом деле они оказываются более сложными. Это объясняется тем, что в пределах исследуемых величин самые сложные зависимости могут носить приближенно линейный характер.

В общей форме прямолинейное уравнение регрессии имеет вид:
y=a₀ + b₁*x₁ + b₂*x₂ + … + b_m*x_m;
где y – результативный признак, исследуема переменная;

x_i – обозначение фактора (независимая переменная);

m – общее число факторов;

a₀ – постоянный (свободный) член уравнения;

b_i – коэффициент регрессии при факторе.

Увеличение результативного признака при изменении фактора x_i на единицу равно коэффициенту регрессии b_i (с положительным знаком); уменьшение – с отрицательным знаком.

Очевидная экономическая интерпретация результатов линейной регрессии одна из основных причин ее применения в исследовании и прогнозировании экономических процессов. В зависимости от числа факторов, влияющих на результативный показатель, различают парную и множественную регрессии.

Кратко изложим основные положения по разработке и использованию в прогнозировании множественных линейных регрессионных моделей (парная регрессия может быть рассмотрена как частный случай множественной). Экономические явления определяются, как правило, большим число совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной переменной y от нескольких объясняющих переменных x₁, x₂, ... x_n Эта задача решается с помощью множественного регрессионного анализа. Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели, включающего отбор факторов и выбор вида уравнения регрессии. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

• 
  Они должны быть количественно измеримы (качественным факторам необходимо придать количественную определенность);
  
• 
  Между факторами не должно быть высокой корреляционной, а тем более функциональной зависимости, т.е. наличия мультиколлинеарности.
  

Включение в модель мультиколлинеарных факторов может привести к следующим последствиям:

• 
  Затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом виде», поскольку факторы связаны между собой;
  
• 
  Параметры линейной регрессии теряют экономический смысл;
  
• 
  Оценки параметров ненадежны, имеют большие стандартные ошибки изменяются с изменениями объема наблюдений.