Вопросы к экзамену Полесский. 29. Тесты гетероскедастичнсоти. 46

• Название: 29. Тесты гетероскедастичнсоти. 46
• Анкор: Вопросы к экзамену Полесский
• Дата: 12.03.2023
• Размер: 5.25 Mb.
• Имя файла: Voprosy_k_ekzamenu_po_distsipline_Ekonometrika_1.doc
• Тип: Документы; #982220
• страница: 7 из 34

Теорема Гаусса – Маркова.

Пусть матрица X коэффициентов уравнений наблюдений имеет полный ранг, а случайные возмущения удовлетворяют четырем условиям:

E(ε1) = E(ε2) = … = E(εn) = 0,

Var(ε1) = Var(ε2) = … = Var(εn) =  σ2

Cov(εi, εj) = 0 при i≠j

Cov(xi,εj) = 0 при всех значениях i и j

В этом случае справедливы следующие утверждения:

а) наилучшая линейная процедура, приводящая к несмещенной и эффективной оценке, имеет вид: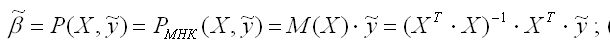

(1)

б) линейная несмещенная эффективная оценка обладает свойством наименьших квадратов:


в) ковариационная матрица оценки вычисляется по правилу:



Г) несмещенная оценка параметра σ2 модели находится по формуле:



С ледствие теоремы Гаусса-Маркова.

Оценка доставляемая процедурой (1) метода наименьших квадратов, может быть вычислена в процессе решения системы двух линейных алгебраических уравнений: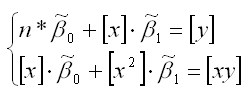



Данная система называется системой нормальных уравнений. Ее коэффициенты и свободные члены определяются по правилам: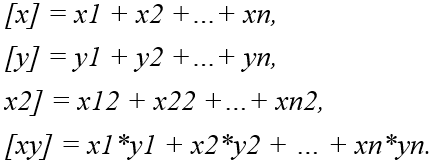



Явный вид решения системы: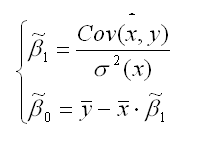

8. Статистические свойства МНК – оценок.

Предположим, что методом наименьших квадратов получена оценка

Для того, чтобы данная оценка могла быть принята за оценку параметра

необходимо и достаточно выполнения трёх статистических свойств:

1) свойства несмещённости;

2) свойства состоятельности;

3) свойства эффективности.

Сделаем следующие предположения об отклонениях єi:

1) величина є iявляется случайной переменной;

2) математическое ожидание єi равно нулю: М (єi) = 0;

3) дисперсия є постоянна: D(єi) = D(єi) = s для всех i, j;

4) значения єi независимы между собой, следовательно, справедливо следующее выражение: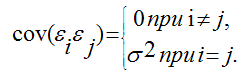



Если данные предпосылки выполняются, то оценки, найденные с помощью метода наименьших квадратов, обладают свойствами несмещённости, состоятельности и эффективности.

Если третье и четвёртое предположения не выполняются, т. е. дисперсия случайных компонент непостоянна и/или значения є коррелируют друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойство эффективности – нет.

Величина



называется несмещённой оценкой параметра

если её выборочное математическое ожидание равно оцениваемому параметру генеральной совокупности:



Отсюда следует, что



где φi – это величина смещения оценки.

Рассмотрим свойство несмещённости МНК-оценок на примере модели парной регрессии.

Необходимо доказать, что оценка

п олученная методом наименьших квадратов, является несмещённой оценкой параметра

для нормальной линейной модели регрессии, т. е. необходимо доказать справедливость равенства