Экзамен по Шарову (Оптика 30-66). 30. Природа света
 Скачать 2.91 Mb. Скачать 2.91 Mb.
|
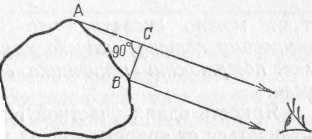
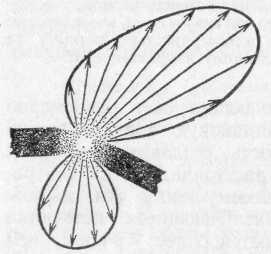
§ 72. Единицы световых величин. В системе световых единиц за исходную величину принята единица силы света. Эта единица имеет условный характер: в качестве единицы силы света принята сила света некоторого эталонного источника. Таким источником, дающим силу света I=1, вначале условились считать пламя свечи, изготовленной строго стандартным образом. Однако этот эталонный источник оказался мало удобным, так как даваемая им сила света несколько изменяется по мере образования «нагара» и, кроме того, зависит от температуры и влажности воздуха. Для установления эталона силы света было предложено много других источников, в частности эталонные электрические лампы накаливания, образцы которых хранятся в крупных государственных измерительных лабораториях и контролируются взаимными сравнениями.•E. В зависимости от диаграммы рассеяния яркость по разным направлениям может быть различна, и вычисление ее представляет очень сложную задачу. Задача эта упрощается, если поверхность рассеивает свет равномерно по всем направлениям. В таком случае и яркость по всем направлениям будет одинаковой и равнойЕсли освещенность Е выражается в люксах, то яркость получится в канделах на квадратный метр. Найдем, например, яркость киноэкрана, если его коэффициент отражения =0,75, а освещенность равна 50 лк. Пользуясь формулой (77.1), имеем Приведем значения яркости освещенных поверхностей (табл. 3), с которыми часто приходится встречаться в жизни Таблица 3. Яркость некоторых освещенных поверхностей (в кд/м2)  34. Световые измерения и измерительные приборы. Световые измерения и измерительные приборы. Измерение световых величин может производиться непосредственно с помощью глаза (визуальные методы) или с помощью фотоэлемента, или термостолбика (объективные методы). Приборы, служащие для измерения световых величин, называются фотометрами. Визуальные методы основаны на свойстве глаза очень хорошо устанавливать равенство яркостей двух смежных поверхностей. В то же время с помощью глаза очень трудно оценить, во сколько раз яркость одной поверхности больше яркости второй. Поэтому во всех визуальных фотометрах роль глаза сводится к установлению равенства яркостей двух смежных площадок, освещаемых сравниваемыми источниками. Так как сравниваемые поверхности делаются диффузно отражающими, то равенство их яркостей соответствует, согласно сказанному в предыдущем параграфе, равенству освещенностей. Освещенность площадки, на которую падает свет от более сильного источника, ослабляется тем или иным способом в известное число раз. Установив равенство освещенностей обеих площадок и зная, во сколько раз ослаблен свет одного из источников, мы можем количественно сравнить силы света обоих источников. Таким образом, во всяком фотометре должны быть два смежных световых поля, одно из которых освещено только одним источником, второе — только другим. Вид сравниваемых полей может быть различен. В большинстве случаев они имеют форму двух смежных полукругов (рис. 164, а) или двух концентрических кругов (рис. 164, б).Оба сравниваемых поля должны освещаться каждое своим источником под одним и тем же углом; глаз наблюдателя также должен рассматривать оба поля под одинаковыми углами зрения. 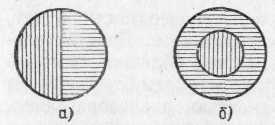 Рис. 164. Вид сравниваемых полей в фотометре На рис. 165 показано устройство одного из простейших фотометров. Свет от сравниваемых источников S1 и S2 падает на белые грани призмы ABC, помещенной внутри зачерненной трубки. Глаз наблюдателя рассматривает призму по направлению СО. Простой фотометр был предложен немецким физиком и химиком Робертом Бунзеном (1811—1899). В этом фотометре световое поле представляет собой экран из белой бумаги, в середине которого небольшая часть поверхности промаслена и благодаря этому просвечивает. Масляное пятно должно иметь резкие края. Два источника света помещаются по обе стороны от экрана и путем ослабления одного из них добиваются, чтобы масляное пятно и остальная часть экрана сделались одинаково яркими. На этом принципе «просвечивающего участка» построены многие более совершенные фотометры. Для того чтобы получить одинаковую освещенность обеих площадок 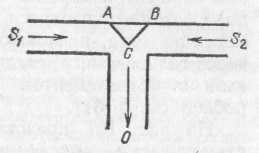 Рис. 165. Устройство простейшего фотометра фотометра, наиболее простым средством является изменение расстояний сравниваемых источников от фотометра при условии применимости закона обратных квадратов (см. § 71). Как мы знаем, освещенность площадки пропорциональна силе света источника и обратно пропорциональна квадрату его расстояния от площадки. Если освещенности обеих площадок фотометра одинаковы, то гдеI1 и I2 — силы света, а R1, R2— расстояния от источников до фотометра. Измерив R1 и R2, мы можем сказать, во сколько раз сила света одного источника больше или меньше силы света другого. Этот способ имеет тот недостаток, что варьировать расстояния R1и R2практически можно «лишь в не очень широких пределах. Другой способ ослабления светового потока от одного из источников состоит в том, что на пути его вводится поглощающее тело, представляющее собой два скользящих друг относительно Друга клина, сделанных из материала, Поглощающего свет (рис. 166). Передвигая их, мы изменяем толщину поглощающего слоя и тем самым изменяем степень поглощения светового потока. Предварительно производится градуирование ослабителя: устанавливается, насколько меняется поглощение при смещении клина на определенное расстояние. 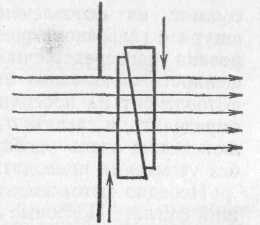 Рис. 166. Устройство для ослабления светового потока, обеспечивающее прохождение лучей без отклонения Существуют фотометры, приспособленные для непосредственного измерения освещенности; такие фотометры называются люксметрами. В фотометрах воспринимающим свет устройством является фотоэлемент. Под действием света фотоэлемент дает электрический ток тем больший, чем больше освещенность фотоэлемента, конечно, при условии, что вся поверхность фотоэлемента равномерно освещена. Таким образом, измерение освещенности с помощью объективного фотометра сводится к измерению тока, протекающего через гальванометр, соединенный с. фотоэлементом (подробнее см. § 181). На рис. 167 представлен схематически люксметр. Он 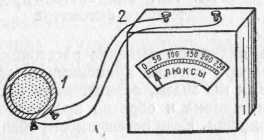 Рис. 167. Люксметр: 1 — фотоэлемент, 2 — гальванометр со шкалой, градуированной в люксах 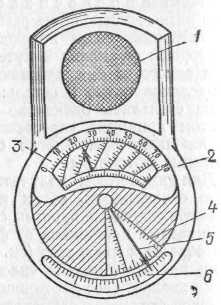 Рис. 168. Экспонометр: 1 — фотоэлемент, 2 — гальванометр, 3— шкала времени экспозиции, 4— шкала чувствительности фотоматериалов, 5 — указатель, 6 — шкала диаметра диафрагмы состоит из фотоэлемента 1, соединенного с помощью шнура с гальванометром 2. Шкала гальванометра градуирована непосредственно в люксах. Для измерения освещенности с помощью этого прибора достаточно положить фотоэлемент на поверхность, освещенность которой хотят определить, и сделать отсчет по шкале. Фотоэлектрические люксметры очень удобны в работе и позволяют быстро и без утомления проводить измерения. Нередко фотоэлемент и гальванометр заключают в общий футляр. Подобные люксметры применяются фотолюбителями для определения освещенности фотографируемого объекта и, следовательно, для правильного выбора времени экспозиции; их называют поэтому экспонометрами (рис. 168). Шкала гальванометра экспонометра, проградуированная в продолжительностях экспозиции, нанесена на полуокружности вращающегося кольца 3, На секторе 4, вращающемся вместе с кольцом 3, нанесены деления, соответствующие чувствительности применяемых фотоматериалов. Указатель 5 устанавливается на деление неподвижной шкалы 6, соответствующее диаметру применяемой при съемке диафрагмы; затем кольцо 3 вращается до совпадения с указателем 5 нужного деления на секторе 6. Тогда стрелка гальванометра указывает экспозицию, нужную для съемки с выбранной диафрагмой при данных фотоматериалах. 35. Прямолинейное распространение света и световые лучи. Прямолинейное распространение света и световые лучи. Наблюдения показывают, что в однородной среде свет также распространяется вдоль прямых линий. Ряд опытов, иллюстрирующих это положение, общеизвестен. При освещении предмета точечным источником получается резкая тень (рис. 172), форма которой подобна форме некоторого сечения предмета, параллельного плоскости экрана; размеры же тени определяются взаимным расположением источника, предмета и экрана в полном соответствии с проецированием при помощи прямых линий. Наблюдающиеся иногда нерезкие тени (полутени) объясняются не отступлением направления распространения 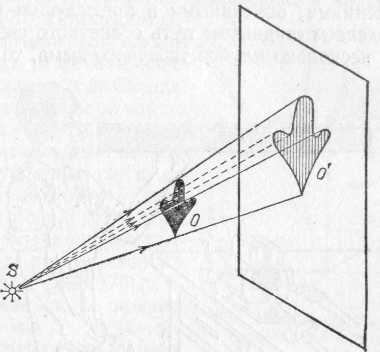 Рис. 172. При освещении точечным источником света S плоского объекта О, параллельного экрану, на экране появляется резкая тень O', подобная этому объекту 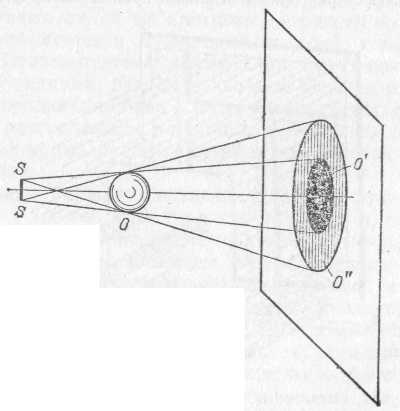 Рис. 173. При освещении шарика О протяженным источником SS появляющаяся на экране тень О' окаймлена полутенью О" света от прямолинейности, а конечными размерами источника света (рис. 173). Всем известен способ, применяемый столярами, проверки «по лучу» прямолинейности кромки отстроганной доски (рис. 174). Явления прямолинейного распространения света представляют полную аналогию с явлениями, описанными в предыдущем параграфе. Если мы сделаем «видимым» путь солнечного света, пустив в комнату несколько клубов табачного дыма, то мы можем повторить опыт с перегородками. Поставим на пути света непрозрачный картон с одним или несколькими небольшими отверстиями, которые, конечно, во много раз превосходят длину световой волны; мы увидим путь света в комнате в виде узких каналов, опирающихся на края отверстий (рис. 175). При любом положении картона эти каналы имеют одно и то же направление: они указывают на Солнце. 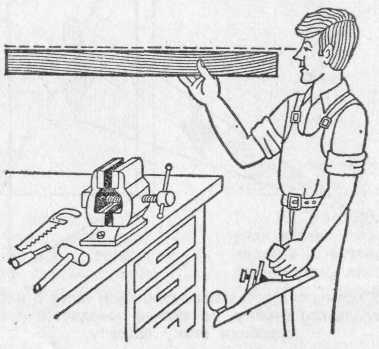 Рис. 174. Проверка прямолинейности кромки «по лучу зрения» 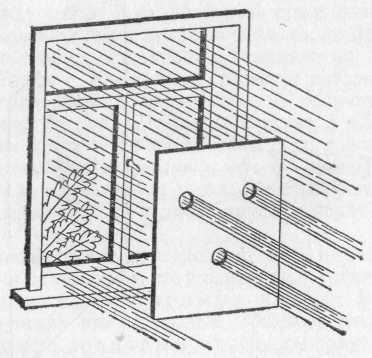 Рис. 175. Пучки, выделенные из плоской световой волны (источник — Солнце) экраном с небольшими отверстиями. Размеры отверстий еще очень велики по сравнению с длиной световой волны Если в затемненной комнате поставить внутри темного ящика с несколькими отверстиями яркую лампочку с маленькой нитью, то путь выходящего света обрисуется в запыленном воздухе в виде расходящихся в разные стороны узких пучков (рис. 176). Отметив на стене ящика положение лампы, мы без труда заметим, что пучки эти пересекаются в том месте, где находится нить лампы. Поступая так же, как мы делали в опытах с волнами на поверхности воды, проведем линии, указывающие направление распространения света. Если выделенные пучки узки, то проведение таких линий не вызывает затруднений. Эти геометрические линии и представляют собой световые лучи. В рассмотренных случаях они будут почти параллельными линиями, направленными на Солнце, или радиусами, перпендикулярными к поверхности сферы, описанной из места расположения источника света (нить лампочки). Вдоль этих прямолинейных лучей и распространяется световая волна. Нередко в учебниках название «световой луч» приписывают тем узким световым пучкам, с помощью которых мы находим направление лучей. Это — неправильное выражение: мы называем лучом геометрическую линию, указывающую направление распространения света, а не самые световые пучки. Конечно, чем уже световой пучок, тем легче и точнее с его помощью отыскать направление распространения света, т. е. определить световой луч. Мы не можем, однако, осуществить бесконечно узкий световой пучок. Уменьшая размеры отверстия, ограничивающего пучок, мы можем уменьшить ширину пучка лишь до извест- 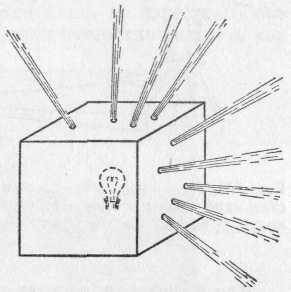 Рис. 176. Пучки, выделенные из сферической световой волны ных пределов. Дальнейшее уменьшение отверстия не только не приводит к уменьшению сечения пучка, но, наоборот, ведет, как показывает опыт, к расширению его. В §41 мы познакомились с этим явлением при изучении волн на поверхности воды (рис. 87, б и в). 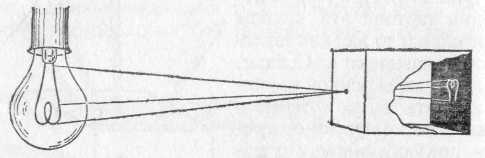 Рис. 177. Изображение предмета в «дырочной камере». Размеры отверстия камеры не показаны. Каждому лучу на самом деле соответствует конус лучей, поэтому изображение нити лампы оказывается слегка размытым Для световых волн это явление можно наблюдать, получая изображение с помощью малого отверстия (так называемая дырочная камера*). Эти наблюдения показывают также, что закон прямолинейного распространения света соблюдается только при известных условиях. Соответствующий опыт изображен на рис. 177. На матовом стекле (или фотопластинке), прикрывающем заднюю стенку дырочной камеры, получается перевернутое изображение расположенного перед ней ярко освещенного объекта (например, нить лампы накаливания). Изображение хорошо воспроизводит форму предмета и не зависит от формы отверстия, если отверстие достаточно мало. Этот результат нетрудно понять. Действительно, от каждой точки источника через отверстие проходит узкий световой пучок, который дает на экране небольшое пятнышко, воспроизводящее форму отверстия. Свет от всего источника в целом дает на экране картину, нарисованную такими светлыми пятнышками, накладывающимися друг на друга. Если размер отверстия таков, что отдельные пятнышки превосходят детали картины, то она получится размытой, плохо передающей объект. Но при достаточно малых размерах отверстия размеры пятнышек будут меньше деталей картины, и изображение получится вполне удовлетворительное. *) Эту камеру называют камерой-обскурой. Рис. 178 воспроизводит фотографию, полученную с помощью такой дырочной фотокамеры. На рис. 179 изображена схема действия «дырочной камеры» и вид изображений, полученных при разных размерах отверстия. Улучшение изображения при уменьшении размеров отверстия наблюдается лишь да известного предела. При дальнейшем уменьшении отверстия резкость кар-  Рис. 178. Фотография, полученная дырочной камерой 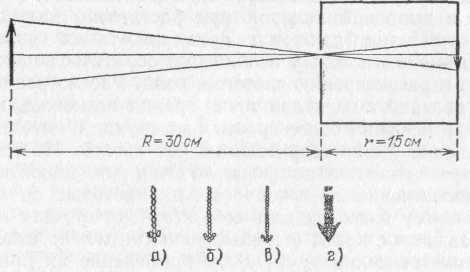 Рис. 179. Схема действия дырочной камеры (вверху) и изображения источника света при разных размерах отверстий (внизу): а) диаметр отверстия около 3 мм; б) около 1 мм; в) около 0,5 мм; г) около 0,03 мм. Источником служит ярко освещенная щель в экране, имеющая вид стрелки ширины около 1 мм. тины начинает ухудшаться (рис. 179, г). При очень малых отверстиях «изображение» совсем теряет сходство с источником. Этот опыт показывает, что светлые пятнышки, которые рисуют отдельные точки источника, при малых размерах отверстия расширяются настолько, что превосходят детали картины, которая размывается тем больше, чем меньше отверстие. Но так как эти пятнышки есть следы световых пучков, вырезаемых отверстием, то опыт обнаруживает расширение светового пучка при чрезмерном уменьшении отверстия. Итак, мы не можем физически выделить сколь угодно узкий пучок. Мы должны ограничиться выделением по возможности узких световых пучков конечной ширины и заменить их затем линиями, представляющими как бы оси этих пучков. Таким образом, световые лучи являются геометрическим понятием. Польза, которую мы извлекаем из этого понятия, состоит в том, что с его помощью мы можем устанавливать направление распространения световой энергии. Законы, определяющие изменение направления лучей, позволяют решать очень важные в оптике задачи об изменении направления распространения световой энергии. Для разбора такого рода задач вполне уместно заменить физическое понятие — световую волну — геометрическим понятием — лучом — и проводить все рассуждения с помощью лучей. Однако далеко не всегда вопрос о характере распространения световых волн может быть решен при помощи понятия о световых лучах. Существует много оптических явлений (опыты с дырочной камерой при достаточно малых размерах отверстия являются примером таких явлений), для понимания которых необходимо обратиться непосредственно к рассмотрению световых волн. Рассмотрение световых явлений с волновой точки зрения возможно, конечно, и для решения более простых задач, где и метод лучей дает вполне удовлетворительные результаты. Но так как метод лучей значительно проще, то его и применяют обычно для рассмотрения всех вопросов, для которых он пригоден. Поэтому надо отдавать себе ясный отчет, для какого круга задач и с какой степенью точности можно использовать геометрические лучи, а где применение их приводит к значительным ошибкам и, следовательно, недопустимо. Таким образом, метод оптики лучей или, как ее называют, геометрической, или лучевой, оптики является приближенным приемом решения, совершенно достаточным для разбора определенного круга вопросов. Поэтому одна из задач изучения оптики состоит в приобретении уменья правильно использовать метод лучей и устанавливать границы его применения 36. Законы отражения и преломления света. Понятие дисперсии. Законы отражения и преломления света. Как уже указывалось (см. §76), возможность видеть несветящиеся предметы связана с тем обстоятельством, что всякое тело частично отражает, а частично пропускает или поглощает падающий на него свет. В § 76 нас интересовали главным образом явления диффузного отражения и пропускания. Именно благодаря этим явлениям свет, падающий на тело, рассеивается в разные стороны, |и мы получаем возможность видеть тело с любой стороны. В частности, благодаря рассеянному свету, хотя и слабому, мы видим отовсюду даже очень хорошие зеркала, которые должны были бы отражать свет только по одному направлению и, следовательно, быть заметными только по одному определенному направлению. Рассеянный свет возникает в этом случае из-за мелких дефектов поверхности, царапин, пылинок и т. д. В настоящей главе мы рассмотрим законы направленного (зеркального) отражения и направленного пропускания (преломления) света. Для того чтобы имело место зеркальное отражение или преломление, поверхность тела должна быть достаточно гладкой (не матовой), а его внутренняя структура — достаточно однородной (не мутной). Это означает, что неровности поверхности, равно как и неоднородности внутреннего строения, должны быть достаточно малы. Как и во всяком физическом явлении, выражение «достаточно мало» или «достаточно велико» означает малое или большое по сравнению с какой-то другой физической величиной, имеющей значение для изучаемого явления. В данном случае такой величиной является длина световой волны. В дальнейшем мы укажем способы ее определения. Здесь же ограничимся указанием, что длина световой волны зависит от окраски светового пучка и имеет значение от 400 нм (для фиолетового цвета) до 760 нм (для красного цвета). Таким образом, для того чтобы поверхность была оптически гладкой, а тело оптически однородным, необходимо, чтобы неровности и неоднородности были значительно меньше микрометра. В этой главе мы ограничимся рассмотрением случая, когда поверхность тела плоская; вопрос о прохождении света через искривленную (сферическую) поверхность будет рассмотрен в следующей главе. Примером плоской поверхности может служить граница раздела воздуха и какой-нибудь жидкости в широком *) сосуде. Соответствующая полировка твердых тел также позволяет получать весьма совершенные плоские поверхности, среди которых металлические поверхности выделяются своей способностью отражать много света. Из стекла легко можно сделать плоские пластинки, которые затем покрываются слоем металла, в результате чего получаются обычные зеркала. Рассмотрим следующий простой опыт. Направим, например, узкий пучок лучей на поверхность воды в большом сосуде (рис. 180). Мы обнаружим, что часть света отразится от поверхности воды, другая часть пройдет из воздуха в воду. Для того чтобы падающий луч SO, отраженный луч ORи прошедший в воду луч ODбыли лучше видны, рекомендуется слегка запылить воздух над сосудом (например, дымом), а в воде, заполняющей сосуд, растворить немного мыла, благодаря чему вода станет слегка мутной. На опыте видно, что вошедший в воду луч не является простым продолжением луча, падающего на границу раздела, а испытывает преломление. При изучении данного явления нас будут интересовать, во-первых, направления отраженного и преломленного лучей и, во вторых, доля отраженной световой энергии и энергии, прошедшей из первой среды во вторую. Рассмотрим вначале отраженные лучи. Накроем поверхность раздела (зеркало) сверху непрозрачной цилиндрической поверхностью АСВ, которую можно сделать, например, из плотной бумаги (рис. 181, а). На дуге АСВ проделаем небольшие отверстия, расположенные, например, через каждые 5°. Тогда окажется, что если луч света пропущен в одно из этих отверстий и направлен по радиусу 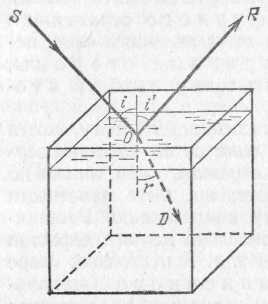 Рис. 180. Преломление и отражение света при падении луча на поверхность воды *) В узких сосудах поверхность жидкости может быть заметно искривлена вследствие явлений капиллярности, шуги АСВ к центру О, то после отражения он выйдет из [прибора через симметричное относительно перпендикуляра NOотверстие в цилиндрическом колпаке, покрывающем зеркало. С какой бы точностью этот опыт ни осуществлялся, на самом совершенном угломерном инструменте результат его остается тем же. Этот надежно установленный результат можно формулировать в виде следующего закона отражения света: луч падающий, луч отраженный и перпендикуляр к отражающей поверхности лежат 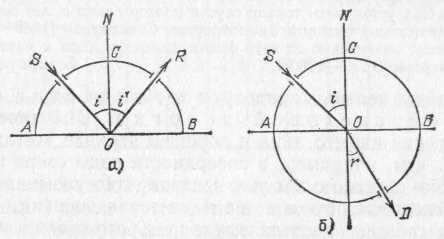 Рис. 181. Измерение угла отражения (а) и преломления (б) в одной плоскости, причем угол отражения луча равен углу падения. Измерение угла, образуемого преломленным лучом [с перпендикуляром к поверхности раздела (угла преломления), можно проделать тем же способом, какой мы использовали при измерении угла отражения. Для этого нужно продолжить цилиндрическую поверхность ACBво вторую среду (рис. 181, б).Точные измерения угла падения iи угла преломления rприводят к следующему закону преломления: луч падающий, луч преломленный и перпендикуляр к поверхности раздела лежат в одной плоскости. Угол падения и угол преломления связаны соотношением где показатель преломления nесть постоянная величина, не зависящая от угла падения и определяющаяся оптическими свойствами граничащих сред. Углы падения i, отражения i' и преломления rпринято измерять от перпендикуляра к поверхности раздела до соответствующего луча. Первые попытки найти закон преломления были сделаны известным александрийским астрономом Клавдием Птолемеем (умер около 168 г.) почти два тысячелетия назад. Однако точность измерений в то время была еще недостаточно высока, и Птолемей пришел к выводу, что отношение углов падения и преломления при заданных средах остается постоянным. Заметим, что для получения правильной зависимости между углом падения и углом преломления нужно измерять эти углы с точностью до нескольких минут; это особенно существенно при небольших углах падения и преломления. При грубых измерениях при небольших углах вместо постоянства отношения синусов углов легко прийти к неправильному выводу о постоянстве отношения самих углов *), как и случилось с Птолемеем. В правильной форме закон преломления был установлен только спустя полторы тысячи лет после Птолемея голландским физиком Виллебрордом Снеллиусом (1580—1626) и, по-видимому, независимо от него французским физиком и математиком Рене Декартом (1596—1650). Перейдем теперь к вопросу о количестве отраженной световой энергии. Мы знаем, что изображение нашего лица в хорошем зеркале всегда более светлое, чем, например, в поверхности воды озера или колодца. Это связано с тем уже неоднократно упоминавшимся обстоятельством, что не вся световая энергия, падающая на границу раздела двух сред, отражается от нее: часть света проникает через границу раздела во вторую среду и проходит через нее насквозь или частично поглощается в ней. Доля отраженной световой энергии зависит от оптических свойств граничащих между собой сред и от угла падения. Если, например, свет падает на стеклянную пластинку перпендикулярно к ее поверхности (угол падения равен нулю), то отражается всего только около 5% световой энергии, а 95% проходит через границу раздела. При увеличении угла падения доля Таблица 4. Доля отраженной энергии при различных углах падения света на поверхность стекла 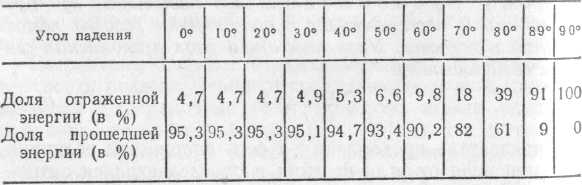 *) Так как при малых углах sin (угол выражен в радианах), то sinii, sinrr, а следовательно, n=sini/sinri/r(причем углы в последнем отношении могут быть выражены ив градусах, ибо отношение однородных величин не зависит от выбора единицы измерения их). отраженной энергии возрастает. В табл. 4 приводится в качестве примера доля отраженной энергии при различных углах падения света на поверхность, разграничивающую воздух и стекло (n=1,555). В табл. 5 приводятся аналогичные данные для поверхности раздела воздух— вода (n=1,333). Таблица 5. Доля отраженной энергии при различных углах падения света на поверхность воды 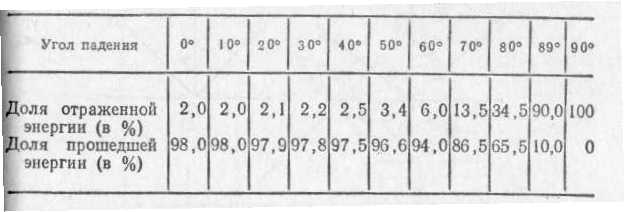 В заключение мы должны сделать оговорку, что закон отражения и закон преломления справедливы только в том случае, если поверхность раздела по своим размерам значительно превосходит длину волны света. Маленькое зеркало, например, действует как маленькое отверстие, с той только разницей, что оно еще изменяет направление падающих на него лучей. Если зеркало имеет размеры, меньшие 0,01 мм, то, так же как при прохождении света через очень малые отверстия, начинают уже заметно сказываться волновые свойства света. В этом случае узкий пучок, отражаясь, расширяется и притом тем значительнее, чем меньше размер зеркала. То же справедливо и по отношению к преломленному пучку. Разъяснение этих явлений будет дано в главе одифракции света. Диспе́рсия све́та (разложение света) — это явление, обусловленное зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты). Экспериментально открыта Ньютоном около 1672 года, хотя теоретически достаточно хорошо объяснена значительно позднее. Пространственной дисперсией называется зависимость тензора диэлектрической проницаемости среды от волнового вектора. такая зависимость вызывает ряд явлений, называемых эффектами пространственной поляризации. Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Сущностью явления дисперсии является неодинаковая скорость распространения лучей света c различной длиной волны в прозрачном веществе — оптической среде (тогда как в вакууме скорость света всегда одинакова, независимо от длины волны и следовательно цвета). Обычно чем больше частота волны, тем больше показатель преломления среды и меньше ее скорость света в ней: у красного цвета максимальная скорость в среде и минимальная степень преломления, у фиолетового цвета минимальная скорость света в среде и максимальная степень преломления. Однако в некоторых веществах (например в парах йода) наблюдается эффект аномальной дисперсии, при котором синие лучи преломляются меньше, чем красные, а другие лучи поглощаются веществом и от наблюдения ускользают. Говоря строже, аномальная дисперсия широко распространена, например, она наблюдается практически у всех газов на частотах вблизи линий поглощения, однако у паров йода она достаточно удобна для наблюдения в оптическом диапазоне, где они очень сильно поглощают свет. Дисперсия света позволила впервые вполне убедительно показать составную природу белого света. Белый свет разлагается на спектр и в результате прохождения через дифракционную решётку или отражения от нее (это не связано с явлением дисперсии, а объясняется природой дифракции). Дифракционный и призматический спектры несколько отличаются: призматический спектр сжат в красной части и растянут в фиолетовой и располагается в порядке убывания длины волны: от красного к фиолетовому; нормальный (дифракционный) спектр — равномерный во всех областях и располагается в порядке возрастания длин волн: от фиолетового к красному. По аналогии с дисперсией света, также дисперсией называются и сходные явления зависимости распространения волн любой другой природы от длины волны (или частоты). По этой причине, например, термин закон дисперсии, применяемый как название количественного соотношения, связывающего частоту и волновое число, применяется не только к электромагнитной волне, но к любому волновому процессу. Дисперсией объясняется факт появления радуги после дождя (точнее тот факт, что радуга разноцветная, а не белая). Дисперсия является причиной хроматических аберраций — одних из аберраций оптических систем, в том числе фотографических и видео-объективов. Коши пришел к формуле, выражающей зависимость показателя преломления от длины волны: где: L — длина волны в вакууме; a, b, c, … — постоянные, значения которых для каждого вещества должны быть определены в опыте. В большинстве случаев можно ограничиться двумя первыми членами формулы Коши. Дисперсия света в природе и искусстве Из-за дисперсии можно наблюдать разные цвета света. Радуга, чьи цвета обусловлены дисперсией, — один из ключевых образов культуры и искусства. Благодаря дисперсии света, можно наблюдать цветную «игру света» на гранях бриллианта и других прозрачных гранёных предметах или материалах. В той или иной степени радужные эффекты обнаруживаются достаточно часто при прохождении света через почти любые прозрачные предметы. В искусстве они могут специально усиливаться, подчеркиваться. Разложение света в спектр (вследствие дисперсии) при преломлении в призме - довольно распространенная тема в изобразительном искусстве. Например, на обложке альбома Dark Side Of The Moon группы Pink Floyd изображено преломление света в призме с разложением в спектр. 37. Интерференция света. Дифракция света. Геометрическая и физическая оптика. Изложенное во втором разделе книги показывает, что можно получить вполне удовлетворительное решение обширного круга вопросов практической оптики, не пользуясь волновыми представлениями о свете. Для этой цели было введено понятие светового луча как линии, указывающей направление распространения световой энергии. Далее, были установлены геометрические правила относительно изменения направления этих лучей при отражении и преломлении света. Пользуясь этими правилами, мы на протяжении глав X, XI и XII разобрали многочисленные и важные задачи практической оптики. Все вопросы, которые могут быть удовлетворительно решены геометрическим путем, составляют содержание геометрической, или лучевой, оптики. Однако даже при рассмотрении этих проблем возникают важные вопросы, касающиеся разрешающей силы оптических приборов, на которые метод геометрической оптики не может дать нужного ответа. Кроме того, существует обширный класс оптических проблем, относящихся главным образом к вопросам взаимодействия света и вещества, для понимания которых надо составить более глубокое представление о природе света. Все эти вопросы составляют содержание так называемой физической оптики, с основами которой мы и познакомимся в этой части. |