Экзамен по Шарову (Оптика 30-66). 30. Природа света

• Название: 30. Природа света
• Дата: 23.05.2023
• Размер: 2.91 Mb.
• Имя файла: Экзамен по Шарову (Оптика 30-66).docx
• Тип: Документы; #1154835
• страница: 3 из 15

§ 124. Опытное осуществление интерференции света. Опи­санные в § 66 явления цветов тонких пленок представляют собой один из наиболее распространенных и легко наблюда­емых случаев интерференции света. Однако условия воз­никновения интерференционной картины в этом случае значительно отличаются от условий, при которых наблюда­ется интерференция волн на поверхности воды (см. §44). В случае волн на поверхности воды мы имели два источника волн (два острия), в случае же интерференции в тон­ких пленках налицо был только один источник света. Воз­никают вопросы, откуда в этом случае берутся две взаимодей­ствующие волны, а также можно ли осуществить интерфе­ренцию света, заставляя взаимодействовать световые волны, посылаемые двумя различными источниками, например двумя лампочками накаливания или двумя участ­ками раскаленного тела. Ответ на последний вопрос дает повседневный опыт. Мы хорошо знаем, что при освещении одного и того же участка светом различных источников интерференционные явления не наблюдаются. Если в ком­нате горят две лампочки, то во всей освещенной обла­сти свет одного источника усиливает освещение, даваемое другим, добавление второго источника не ведет к образова­нию максимумов и минимумов освещенности.

Причина этого лежит в том, что для получения устойчи­вой интерференционной картины, необходимо, как указы­валось в § 44, обеспечить когерентность, или согласо­вание, двух систем волн. Источники должны испускать когерентные волны, т. е. волны, обладающие одним периодом и неизменной разностью фаз на протяжении вре­мени, достаточного для наблюдения. Все наши способы наблюдения (глаз, фотопластинка и т. д.) требуют срав­нительно длительных промежутков времени, измеряемых тысячными и более долями секунды. В независимых же источниках свет испускают различные атомы, условия излучения которых быстро и беспорядочно меняются. В на­стоящее время мы имеем ряд данных, которые позволяют считать, что такие изменения происходят в лучшем случае примерно через 10^-8 с, а обычно гораздо быстрее. Таким образом, интерференционная картина, получаемая от неза­висимых источников, сохраняется неизменной очень корот­кое время, а затем сменяется другой, с иным расположением максимумов и минимумов. Так как время, необходимое для наблюдения, измеряется, как сказано, тысячными и более долями секунды, то за это время интерференционные кар­тины успеют смениться миллионы раз. Мы наблюдаем ре­зультат наложения этих картин. Понятно, что такое наложение размывает картину, не оставляя никаких следов интерференционных максимумов и минимумов. Та­ким образом, становится понятным, почему при наблюде­нии действия двух независимых некогерентных источников света мы не обнаруживаем интерференции. Однако от двух разных лазерных источников света явле­ния интерференции могут наблюдаться.

Для наблюдения интерференции приходится прибегать к искусственному приему. Этот прием состоит в том, что за­ставляют интерферировать части одной и той же волны, идущие от единственного источника и достигающие точки наблюдения по разным путям, благодаря чему между ними возникает некоторая раз­ность хода. Когерентность обеспечивается тем, что обе интерферирующие волны одновременно испускаются одним источником. В опытах с тонкими пленками вол­на, идущая от источника, расщепляется на две путем отражения от передней и задней поверхностей пленки.

Той же цели можно достигнуть и другими приспособле­ниями, например при помощи так называемой бипризмы *) (рис. 263, а), где для раздвоения волны использовано пре­ломление. Здесь дело происходит так, как если бы два коге­рентных источника были расположены в точках S₁ и S₂.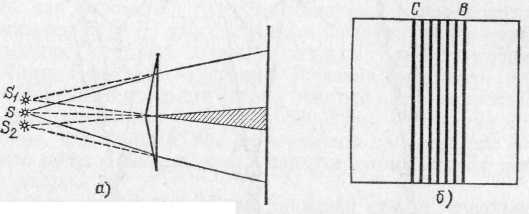



Рис. 263. Наблюдение интерференции света с помощью бипризмы Фре­неля: а) схема опыта (вид сверху); б) интерференционная картина

В действительности же имеется единственный ре­альный источник S. Этот источник представляет собой узкую освещенную щель, параллельную ребру бипризмы. Волна, идущая от источника S, раздваивается путем пре­ломления в двух половинах бипризмы и доходит до точек экрана по двум различным путям, т. е. с определенной раз­ностью хода. На экране будет наблюдаться система чередую­щихся светлых и темных полос, параллельных ребру би­призмы (рис. 263, б).Полосы располагаются в той части экрана, где происходит перекрывание световых пучков, идущих от двух половинок бипризмы (заштрихованная об­ласть на рис. 263, а).

Разность хода между обоими интерферирующими лу­чами ограничена по следующим соображениям. Атом в каж-

*) Би — от латинского слова bis — дважды; бипризма — двойная призма

дый акт излучения испускает систему волн (волновой цуг), которая распространяется во времени и пространстве, со­храняя синусоидальность (см. § 5). Однако длительность цуга ограничена затуханием колебаний электрона в самом атоме и столкновениями этого атома с другими атомами. Длина цуга, или, как ее называют, длина когерентности такого цуга, в самых благоприятных условиях излучения достигает около 30 см, а временная длительность его не больше 10^-8—10^-9 с. Необходимое условие интерференции заключается в том, чтобы разность хода (разность опти­ческих путей, т. е. произведения показателей преломления на геометрические длины путей) обоих лучей была не больше длины когерентности порождающего их волнового цуга. Рис. 264 иллюстрирует это условие.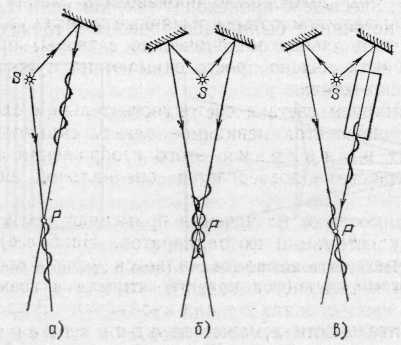



Рис. 264. К интерференции двух цугов световых волн: а) разность хода обоих цугов волн больше длины когерентности — интерференции нет; б) разность хода равна нулю— интерференция есть; в) на пути одного из цугов помещена стеклянная пластинка (n>1), разность хода обоих цугов больше длины когерентности — интерференции нет

Идеальным источником света служит квантовый генератор (лазер), который по своей физической природе, как источ­ник вынужденного излучения, является когерентным (см. §202). Длина когерентности лазерного цуга простирается на тысячи километров, а длительность цуга достигает со­тых долей секунды. Благодаря квантовому генератору уда­лось создать новую область оптики — когерентную оптику, имеющую огромные теоретические и технические достиже­ния и необозримые перспективы.

Если источник света в опыте с бипризмой (опыт Френеля) испускает белый свет, то мы увидим цветную интерферен­ционную картину, как это имеет место и при наблюдении интерференции в тонких пленках. Если же источник посы­лает одноцветный, т. е. монохроматический, свет (напри­мер, свет от дугового разряда в газе, прошедший сквозь соответствующий светофильтр), то интерференционная кар­тина состоит из чередующихся светлых и темных полос. Положение этих полое зависит от цвета, так что места, соответствующие минимуму в одном цвете, могут оказаться местами максимума для другого цвета. Это означает, что расстояние от источников S₁и S₂ до рассматриваемого места экрана выражается четным числом полуволн одного цвета и нечетным числом полуволн другого цвета. Иными сло­вами, длины световых волн различного цвета различны. Таким образом, свет различного цвета физически характеризуется различием в длинах волн.

Так как положение интерференционных полос зависит от длины волны, то с помощью опыта Френеля можно опре­делить длину световой волны, произведя соответствующие измерения. Подобные измерения показали, например, что пламя, окрашенное парами натрия (желтый цвет), испускает свет двух длин волн — 589,0 и 589,6 нм. Измерения по­казывают, что длина волны уменьшается при переходе от красного света к фиолетовому в порядке расположения цве­тов в радуге.

Известно, что оценка цвета, даваемая глазом, довольно неопределенна, так что под названием красного или желтого цвета, например, мы понимаем довольно раз­нообразные оттенки. Поэтому указание длины волны для каждого такого цвета имеет ориентировочный характер. Фиолетовый цвет соответствует длинам волн от 400 до 450 нм, синий — от 450 до 480 нм, голубой — от 480 до 500 нм, зеленый — от 500 до 560 нм, желтый— от 560 до 590 нм, оранжевый — от 590 до 620 нм, красный — от 620 до 760 нм. Таким образом, указание цвета характеризует свет прибли­женно. Наоборот, длина волны является точной количественной характеристикой цвета, которой и пользуются во всех научных измерениях.

§ 125. Объяснение цветов тонких пленок. Опираясь на ска­занное в предыдущем параграфе, мы можем составить себе отчетливое представление о происхождении цветов тонких пленок. При освещении прозрачной пленки часть световой волны отражается от передней поверхности, часть от задней, благодаря чему встречаются волны с некоторой разностью хода. Нетрудно видеть (рис. 265), что эта разность хода за­висит от толщины пленки, определяющей длину пути волны внутри пленки. В тех местах пленки, где эта разность хода достигает четного числа полуволн, обе части волны взаимно усиливают друг друга (максимум), там же, где разность хода выражается нечетным числом полуволн, имеет место взаимное ослабление (минимум). Так как пленка в разных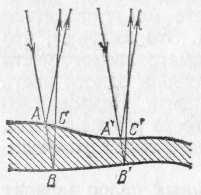



Рис. 265. Разность хода (AВС, А'В'С) двух частей световой волны, отражающейся от передней и задней поверхностей тонкой плен­ки, зависит от толщины пленки в месте от­ражения

местах может иметь разную толщину, то области макси­мумов и минимумов дают на ее поверхности картину темных и светлых мест, если опыт производится в монохро­матическом (одноцветном) свете, или картину разноцветных полос, если применяется белый свет. Для наблюдения этой интерференционной картины, надо рассматривать поверхность пленки, т. е. аккомодиро­вать глаз на ее поверхность. Это значит, что интерферен­ционная картина локализована (находится) вблизи поверх­ности пленки. В некоторых случаях это можно обнаружить, перемещая вдоль поверхности пленки миниатюрный прием­ник света (фотоэлемент или термоэлемент), соединенный с гальванометром. Чередующиеся при перемещении фотопри­емника максимальные и минимальные показания гальвано­метра подтверждают неравномерное распределение осве­щенности в интерференционном световом поле около пленки. Картина интерференционных полос в подобных опытах пока­зывает, каким образом распределены области одинаковой толщины в пленке, и позволяет в известной мере судить о виде пленки. Так, рис. 266 показывает, что пленка имеет вид вертикального клина. Такую пленку можно изготовить, окунув проволочное кольцо в мыльный раствор и располо­жив кольцо вертикально. Под действием силы тяжести раствор стекает книзу и пленка принимает форму клина, пологого вверху и постепенно расширяющегося книзу (рис. 266, б).Рассматривая такой клин, освещенный светом Солнца или проекционного фонаря, мы увидим ряд горизонтальных цветных полос, параллельных ребру клина, По­лосы повторяются в известной последовательности цветов. В монохроматическом свете (красный светофильтр) получим чередование светлых (красных) и темных полос той же фор­мы (см. рис. IV на форзаце). В пленках со случайным рас­пределением толщины (например, в пленке нефти на поверх­ности воды) расположение полос максимумов и минимумов



Рис. 266. Интерференционные полосы (а) в клинообразной пленке (б): ширина полос уменьшается книзу по мере увеличения толщины пленки; сечение пленки изображено по толщине сильно преувеличенным. Тол­щина ее даже внизу не превосходит нескольких микрометров

имеет прихотливый характер. Понятна также и роль угла, под которым наблюдается пленка. В зависимости от на­правления наблюдения и от угла падения света на плен­ку, путь света внутри пленки будет большим или меньшим, а следовательно, разность хода между частями волны, отра­женными от передней и задней поверхностей пленки, будет различной.

§ 126. Кольца Ньютона. Прихотливый вид интерференци­онных картин в тонких пленках объясняется, как сказано, случайными неравномерностями в толщине пленки. В плен­ке, имеющей вид клина, области одинаковой толщины вытя­нуты вдоль ребра клина и в соответствии с этим так же расположены темные и светлые (цветные) полосы интерфе­ренции.

Очень важным видоизменением опыта с клинообразной пленкой является опыт, произведенный еще в 1675 г. Ан­глийский физик и математик Исаак Ньютон (1643—1727) наблюдал цвета тонкой прослойки воздуха, заключенной между плоским стеклом и выпуклой поверхностью объектива астрономического рефрактора. Радиус кривизны выпук­лой поверхности объектива в опыте Ньютона был около 10 м, поэтому толщина прослойки воздуха между плотно сжатыми стеклами очень медленно и правильно возрастала от места соприкосновения стекол (где она равна нулю) к на­ружным частям объектива.

Если смотреть на такую систему, то темное место сопри­косновения обоих стекол оказывается окруженным светлой кольцевой полосой, которая постепенно переходит в темную, вновь сменяется светлой и т. д. По мере увеличения диамет­ра кольца толщина воздушной прослойки возрастает нерав­номерно, воздушный клин становится все круче и соответ­ственно ширина кольцевых полос, т. е. расстояние между двумя соседними минимумами, становится меньше. Такова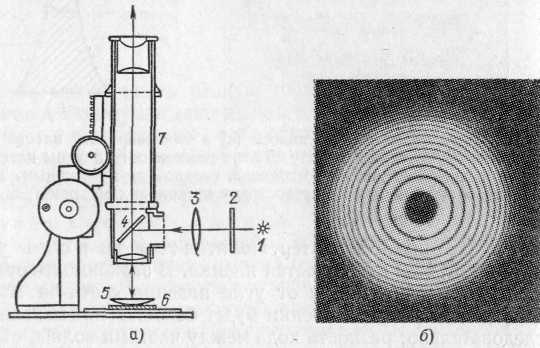



Рис. 267. Наблюдение интерференционных колец Ньютона: а) схема опыта; б) интерференционные кольца. 1 — источник света (лампочка с фильтром 2, или натриевая горелка), 3 — вспомогательный конден­сор, 4 — стеклянная пластинка, отражающая свет, 5 — длинно­фокусная линза и 6 — плоская пластинка, образующие воздушную прослойку, 7 — микроскоп для наблюдения колец и промера их диа­метра

картина, наблюдаемая в монохроматическом свете; в белом свете наблюдается система цветных колец, постепенно пере­ходящих друг в друга. По мере удаления от центрального темного пятна цветные полосы становятся все уже и беле­соватее благодаря перекрытию цветов, пока, наконец, не исчезают всякие следы интерференционной картины.

На основании изложенного выше нетрудно понять, по­чему интерференционная картина имеет в данном случае вид системы концентрических колец. Места равной толщины в воздушной прослойке, которые соответствуют местам с одинаковой разностью хода световых волн, имеют форму окружностей. По этим окружностям и располагаются места равной интенсивности в интерференционной картине.

Удобное расположение приборов, позволяющее наблю­дать и промерять кольца Ньютона, изображено на рис. 267. На столике микроскопа с небольшим увеличением рас­положено плоское стекло, сложенное с линзой малой кривизны. Наблюдение ведется через микроскоп по направле­нию, перпендикулярному к плоскости стекла. Для того чтобы освещающий свет также падал перпендикулярно к плоскос­ти стекла, заставляют свет источника отражаться от стек­лянной пластинки, поставлен­ной под углом 45° к оси ми­кроскопа. Таким образом, ин­терференционная картина рас­сматривается сквозь эту стек­лянную пластинку. Практиче­ски пластинка не мешает наб­людению колец, ибо сквозь нее проходит вполне достаточ­но света. Для усиления осве­щения можно применять кон­денсор. Источником света слу­жит горелка, пламя которой окрашено парами натрия (мо­нохроматический свет), или лампочка накаливания, кото­рую можно прикрывать цвет­ными светофильтрами.

127. Определение длины световой волны с помощью колец Ньютона.

Для того чтобы использовать интер­ференционные явления, в частности кольца Ньютона для измерения дли­ны волны, надо подробнее рассмот­реть условия образования максиму­мов и минимумов света.

При падении света на пленку или тонкую пластинку часть света

проходит сквозь нее, а часть отражается. Предположим, что монохрома­тический свет длины волны падает на пластинку перпендикулярно к ее поверхности. Будем рассматривать малый участок пластинки, считая его плоскопараллельным. На рис. 268 изображен ход лучей в пластин-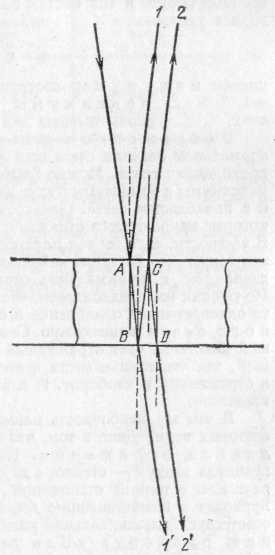



Рис. 268. Ход отраженных и про­ходящих лучей при двукратном отражении в пленке

ке, причем для наглядности лучи изображены не вполне перпендику­лярными к ней. В отраженном свете имеем луч 1, отраженный от верхней поверхности пластинки и луч 2, отраженный от нижней по­верхности. В проходящем — луч 1', прямо прошедший через пластинку и луч 2', отразившийся по одному разу от нижней и от верх­ней поверхностей *).

Рассмотрим сначала проходящие лучи. Лучи 1' и 2' обладают разностью хода, так как первый прошел через нашу пленку один раз, а второй — три раза. Образовавшаяся разность хода при нормальном падении света есть AB+BC+CD—АВ=ВС+CD=2h, где h— толщина пластинки. Если эта разность хода равна целому числу волн, т. е. четному числу полуволн, то лучи усили­вают друг друга; если же разность хода равна нечетному числу полуволн, то лучи взаимно ослабляются. Итак, максимумы и миниму­мы получаются в тех местах пластинки, толщина которых hудовлет­воряет условию



причем минимумы соответствуют нечетному значению n=1, 3, 5, ..., максимумы соответствуют четному значению n=2, 4, ... Таковы выводы для проходящего света.

В отраженном свете разность хода между лучами 1 и 2 при нормальном падении света есть AB+BC=2h, т. е. такая же, как и для проходящего света. Можно было бы думать, что и в отраженном свете максимумы и минимумы будут на тех же местах пластинки, что и в проходящем свете. Однако это означало бы, что места пластинки, которые меньше всего отражают света, меньше всего и пропускают его. В частности, если бы вся пластинка имела одну и ту же толщину и при­том такую, что 2h равно нечетному числу полуволн, то такая пластинка давала бы и минимальное отражение и минимальное пропускание. Но так как мы предполагаем, что пластинка не поглощает света, то одновременное ослабление и отраженного, и пропущен­ного света невозможно. Само собой разумеется, что в непоглощающей пластинке свет отраженный должен дополнять свет прошед­ший, так что темные места в проходящем свете соответствуют светлым в отраженном и наоборот. И действительно, опыт подтверждает это за­ключение.

В чем же ошибочность нашего расчета интерференции отраженных световых волн? Дело в том, что мы не учли различия в ус­ловиях отражения. Некоторые из отражений имеют место на границах воздух — стекло, а другие на границах стекло — воздух (если речь идет о тонкой стеклянной пластинке в воздухе). Это различие приводит к возникновению дополнительной разности фаз, которая со­ответствует дополнительной разности хода, равной /2.Поэтому пол­ная разность хода для лучей, отраженных от верх­ней и нижней поверхностей пластинки толщиной h, равняется 2h+/2. Места минимумов соответствуют условию



где m— нечетное число; места максимумов — четным значениям m. Следовательно, максимумы и минимумы получаются в тех местах пла-

*) Как в проходящем, так и в отраженном свете имеются еще и лучи, испытавшие многократное отражение. Но они настолько слабее первых двух, что их можно не принимать в расчет.

станки, толщина которых hудовлетворяет условию



причем (m—1) обозначено через n. Минимумы соответствуют четным значениям n=0, 2, 4, ..., максимумы соответствуют нечетным значениям n=1, 3, 5, ...

Сопоставим результаты, полученные для определения положения максимумов и минимумов в проходящем и отраженном свете. Поло­жения максимумов и минимумов соответствуют толщине пленки, опре­деляемой из условия: 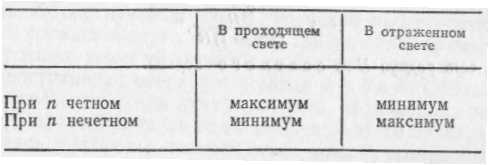, причем:



Таким образом, области максимумов в проходящем свете соответ­ствуют областям минимумов в отраженном и наоборот — в согласии о опытом и в высказанными выше соображениями.

Применительно к кольцам Ньютона, которые обычно наблюдаются в отраженном свете (§ 126), получаем, что места максимумов со­ответствуют нечетным значениям n=1, 3, 5, ..., а места минимумов — четным n=0, 2, 4, ... Центральный (нулевой n=0) минимум имеет вид темного кружка, следующее пер-

мое темное кольцо соответствует

n=2, второе n=4 и т. д. Вообще но­мер N темного кольца связан с чис­лом я соотношением N=n/2.Номер N светлого кольца выражается че­рез nформулой N=(n+1)/2.

Вместо определения толщины hтого места воздушной прослойки, которое соответствует кольцу номе­ра N, удобнее измерять диаметр или радиус соответствующего кольца. Из рис. 269 следует: R²=(R—h)²+r²и, следовательно, толщина прослойки hсвязана с радиусом кольца rи радиусом линзы Rсоот­ношением



Для опытов с кольцами Ньютона пользуются линзами о очень боль­шим радиусом R(несколько метров). Поэтому можно пренебречь вели­чиной ft по сравнению с 2Rи упростить последнее соотношение, запи­сав: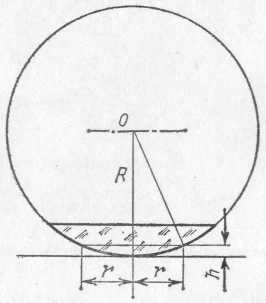





Рис. 269. К расчету радиусов колец Ньютона

Итак, для определения длины волны с помощью колец Ньютона имеем



Если измеряются радиусы темных колец, то номер кольца N=n/2. В таком случае длина волны выразится формулой



где r_N есть радиус N-готемного кольца.

Проводя измерения радиусов светлых колец, мы должны иметь в виду, что N={n+1)/2.В соответствии с этим получаем соотношение



где r_Nесть радиус N-ro светлого кольца.

ДИФРАКЦИЯ СВЕТА