Экзамен по Шарову (Оптика 30-66). 30. Природа света
 Скачать 2.91 Mb. Скачать 2.91 Mb.
|
|
§ 90. Применения формулы тонкой линзы. Действительные и мнимые изображения. Предположим, что светящаяся точка S, лежащая на главной оси линзы, удаляется от линзы на очень большое расстояние. В этом случае лучи, падающие на линзу, будут стремиться стать параллельными ее главной оси. Мы видели в §88, что после преломления в линзе эти лучи соберутся в фокусе F' линзы. В формуле (89.6) при удалении источника на очень большое расстояние величина На стремится к нулю, и мы получаем т. е. можно сказать, что фокус F' есть изображение «бесконечно удаленной» точки. Примером практически бесконечно удаленного источника может служить любое небесное тело. Следовательно, изображения звезд, Солнца и т. д. будут находиться в фокусе линзы. Достаточно далекие от линзы земные источники света также дают изображение в ее фокусе. *) Стигма значит по-гречески точка, стигматический — точечный, частица «а» впереди слова — знак отрицания. Астигматический значит неточечный Предположим теперь, что изображение некоторой точки удалено на очень большое расстояние, т. е. из линзы выходит пучок световых лучей, параллельных главной оси. В этом случае, как мы видели в § 88, источник должен находиться в переднем фокусе линзы F(рис. 196). Этот вывод следует и из формулы (89.6). Действительно, полагая, что изображение находится в бесконечности, получаем 1/а'=0; при этом расстояние источника от линзы равно фокусному расстоянию: а=f=f'. Различные линзы отличаются одна от другой расположением центров образующих их сферических поверхностей, 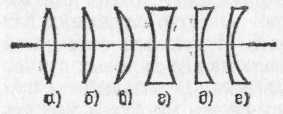 Рис. 198. Различные типы линз. Если материал линз преломляет сильнее, чем окружающая среда, то типы а, б, в — собирающие; типы г, д, е — рассеивающие их радиусами и показателями преломления вещества, из которого сделаны линзы. На рис. 198 представлены шесть основных типов линз. Если параллельные лучи после преломления в линзе сходятся, действительно пересекаясь в некоторой точке, лежащей по другую сторону линзы, то линза называется собирающей или положительной (рис. 199, а). Если же 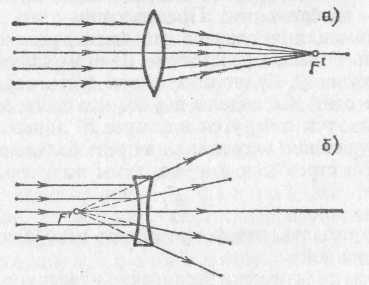 Рис. 199. Действительный фокус собирающей линзы (а) и мнимый фокус рассеивающей линзы (б) параллельные лучи после преломления в линзе становятся расходящимися (рис. 199, б),то линза называется рассеивающей или отрицательной. В случае рассеивающей линзы в фокусе пересекаются не преломленные лучи, а их воображаемые продолжения; при этом фокус лежит с той же стороны от линзы, с которой падает на линзу параллельный пучок лучей. Фокусы в этом случае называются мнимыми (рис. 199, б). Обычно материал линзы преломляет сильнее, чем окружающая среда (например, стеклянная линза в воздухе). Тогда собирающими линзами являются линзы, утолщающиеся от краев к середине,— двояковыпуклая и плосковыпуклая линзы и положительный мениск (вогнуто-выпуклая линза; рис. 198, а—в).Рассеивающими линзами являются линзы, становящиеся тоньше к середине: двояковогнутая, плосковогнутая линзы и отрицательный мениск 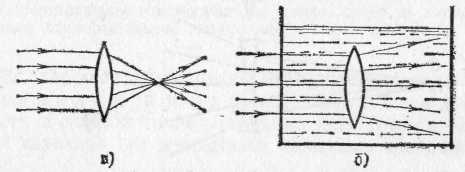 Рис. 200. Двояковыпуклые линзы: а) стеклянная в воздухе — собирающая; б) воздушная в воде — рассеивающая (выпукло-вогнутая линза; 198, г — д). Если материал линзы преломляет слабее, чем окружающая среда, т. е. относительный показатель преломления n<1,то, наоборот, линзы а, б, в (рис. 198) будут рассеивающими, а линзы г, д, е — собирающими. Такие линзы можно получить, например, образовав в воде двумя часовыми стеклами, склеенными воском, воздушную полость соответствующей формы (рис. 200). Перейдем к рассмотрению светящихся точек, находящихся на конечном расстоянии от линзы. Будем всегда считать источники расположенными слева от линзы. Что касается изображений, то в зависимости от вида линзы и положения источника относительно нее изображение S' может находиться как справа, так и слева от линзы. Если изображение лежит справа от линзы, то это означает, что оно образовано сходящимся пучком лучей (рис. 201, а),т. е. лучей, которые действительно проходят через точку S'. Изображение в этом случае называется действительным. Оно может быть получено на экране, фотопластинке и т. п. Восстановив ход лучей, приведших к образованию изображения, мы можем всегда найти местоположение источника, хотя практически это обычно связано с некоторыми трудностями. Предположим теперь, что изображение лежит слева от линзы, т. е. с той же стороны от нее, как и источник. Это означает, что пучок лучей, расходящихся от источника, после преломления в линзе становится еще более расходящимся, и в точке S' пересекаются лишь воображаемые продолжения преломленных лучей (рис. 201, б). Изображение в этом случае называется мнимым. 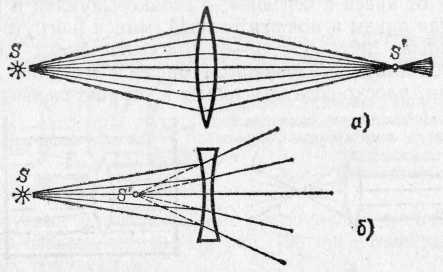 Рис. 201. Источник и действительное изображение лежат с разных сторон от линзы (а); мнимое изображение находится с той же стороны от линзы, что и источник (б) Укоренившийся в оптике термин «мнимое изображение» может привести к некоторым недоразумениям. В действительности ничего «мнимого» в этом случае, конечно, нет. Особенностью мнимых изображений является то, что их нельзя получить непосредственно на экране, фотопластинке и т. п. Например, если поместить в точке S' (рис. 201, б)очень маленький экран, не мешающий попаданию основной части лучей на линзу, то мы не получим на нем светящейся точки. Однако расходящийся пучок лучей, воображаемые продолжения которых пересекаются в мнимом изображении, сам по себе не имеет ничего «мнимого». Этот пучок можно превратить в сходящийся пучок, если на пути его поставить надлежащим образом выбранную собирающую линзу. Тогда на экране или фотопластинке мы будем иметь реальное изображение S" светящейся точки S (рис. 202), которое в то же время можно рассматривать как изображение «мнимой точки» S'. Роль подобной собирающей линзы выполняет также глаз человека; на светочувствительной оболочке глаза — сетчатке — собираются расходящиеся от источников света лучи. Пучок расходящихся лучей, исходят ли они от реального точечного источника S или от его мнимого изображения S', может быть собран оптической системой глаза в одну точку на сетчатке. В повседневной жизни наблюдатель приобретает привычку автоматически восстанавливать ход лучей, давших изображение на сетчатке, и определять местоположение источника. Когда в глаз попадает расходящийся пучок лучей (с вершиной в S'),изображенный на 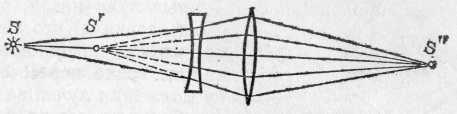 Рис. 202. Превращение расходящегося пучка лучей в сходящийся с помощью вспомогательной собирающей линзы (например, глаза) рис. 202, то, «восстанавливая» место, откуда вышли эти лучи, мы видим в точке S' источник, хотя в действительности в данной точке источника нет. Этот-то воображаемый источник мы и называем «мнимым» изображением точки S. Пользуясь формулой (89.6), нетрудно проследить, как меняется положение изображения по мере перемещения источника вдоль главной оптической оси (см. упражнения 31, 32 в конце этой главы), 42. Плоские и сферические зеркала. Изображение точечного источника и протяженного объекта в плоском зеркале. Изображение точечного источника в сферическом зеркале. Мы переходим теперь к задаче нахождения изображений при отражении света от различного типа зеркал. Законы образования изображений светящихся точек при отражении в зеркале и при преломлении в линзе во многом аналогичны. Эта аналогия, конечно, не случайна; она обусловлена тем, что формально, как мы видели в гл. IX, закон отражения является частным случаем закона преломления (при n=—1). Наиболее просто решается поставленная нами задача для отражения световых лучей от плоского зеркала. Вместе с тем отражение света от плоского зеркала представляет собой наиболее простой и общеизвестный случай образования мнимых изображений, рассмотренных в предыдущем параграфе. Пусть пучок лучей от точечного источника S (рис, 203) падает на плоское зеркало (металлическое зеркало, поверхность воды и т. д.). Проследим, что произойдет с этим конусом лучей, имеющим вершину в точке S. Возьмем два произвольных луча SAи SB. Каждый из них отразится по закону отражения, и угол каждого из них с нормалью останется после отражения неизменным. Следовательно, останется неизменным и угол между лучами после отражения. Этот угол между отраженными лучами можно изобразить на рисунке, продолжив отраженные лучи назад, за плоскость зеркала, что показано на чертеже штриховыми линиями. Точка пересечения S' продолжения лучей за зеркалом будет лежать на той же нормали к зеркалу, что и точка S, и на том же расстоянии от плоскости зеркала, в чем легко убедиться из равенства треугольников SAOи S'AOили SBOи S'BO. Ввиду того что рассмотренные лучи SAи SBбыли совершенно произвольными, мы вправе установленные для них результаты отражения от плоского зеркала распространить на весь световой пучок. Следовательно, мы можем утверждать, что при отражении от плоского зеркала пучок световых лучей, исходящих из одной точки, превращается в световой пучок, в котором продолжения всех световых лучей снова пересекаются, в одной и той же точке. В результате наблюдателю, помещенному на пути отраженных лучей, они будут казаться пересекающимися в точке S', и эта точка будет мнимым изображением точки S. Изображение будет мнимым в указанном выше смысле: никаких лучей в точке S' за зеркалом нет, но точка S' является вершиной пучка лучей, повернутого после отражения от зеркала. Рассмотрение мнимого изображения светящейся точки в плоском зеркале и сделанные выводы о положении этого изображения «за зеркалом» позволяют легко найти также изображение протяженного объекта в плоском зеркале. Пусть перед зеркалом находится прямолинейный светящийся отрезок АВ (рис. 204, а). Выполняя по найденному рецепту построение точек A' и В' и соединяя их прямой, мы получим изображение всех точек отрезка. 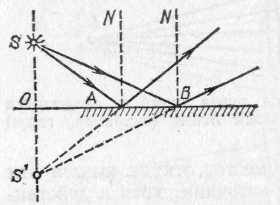 Рис. 203. Образование мнимого изображения точки в плоском зеркале Это вытекает из элементарных геометрических соображений. Так как отрезок АВ был выбран совершенно произвольно, то точно так же можно построить изображение любого 'предмета. При этом из параллельности между собой всех  Рис. 204. а) Образование мнимого изображения прямолинейного отрезка в плоском зеркале. 6) Наблюдателю кажется, что свеча горит в бутылке с водой, расположенной за стеклянной пластинкой там, где находится мнимое изображение свечи в этой пластинке нормалей к зеркалу ясно, что размеры мнимого изображения в плоском зеркале равны размерам предмета, поставленного перед зеркалом. В решении, найденном для случая отражения световых пучков от плоского зеркала, необходимо подчеркнуть, что каждая точка светящегося объекта изобразится в плоском зеркале также в виде точки (т. е. стигматически). Переходим теперь к рассмотрению сферических зеркал. На рис. 205 изображено сечение AРВ вогнутого сферического зеркала радиуса R; С — центр сферы. Средняя точка имеющейся части сферической поверхности называется полюсом зеркала Р. Нормаль к зеркалу, проходящая через центр зеркала и через его полюс, называется главной типической осью зеркала. Нормали к зеркалу, проведенные в других точках его поверхности и также, конечно, проходящие через центр зеркала С, носят название побочных оптических осей. Одна из них (МС) показана на рис. 205. Все 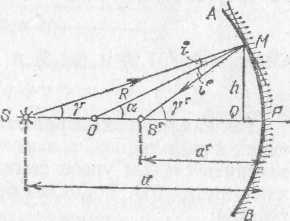 Рис. 205. Отражение от сферического зеркала луча SM, выходящего из точки S на оси нормали к сферической поверхности, конечно, равноправны, и выделение главной оптической оси среди побочных не является существенным *). Диаметр окружности, ограничивающей сферическое зеркало, носит название отверстия зеркала. Все дальнейшее есть упрощенное повторение сказанного в §§ 88, 89 относительно линз. Пусть точечный источник света S расположен на главной оси зеркала на расстоянии SP=aот полюса. Так же, как и в случае линз, рассмотрим луч SM, принадлежащий к узкому пучку, т. е. образующий с осью малый угол у и падающий на зеркало в точке М на высоте hнад осью, так что hмало по сравнению с а и с радиусом зеркала R. Отраженный луч пересечет ось в точке S' на расстоянии S'Р=а' от полюса. Угол, образуемый отраженным лучом с осью, обозначим '. Он также будет мал. Очевидно, СМ есть перпендикуляр к поверхности зеркала в точке падения, i— угол падения, i' — угол отражения. По закону отражения Обозначим буквой угол, образуемый радиусом СМ с осью. Из треугольника SMCимеем из треугольника CMS' Складывая (91.2) и (91.3) и учитывая, что i=i', находим Так как мы рассматриваем узкий пучок лучей, прилегающих к главной оси, т. е. углы ,'и малы, то мы можем заменить синусы углов самими углами и пренебречь длиной отрезка PQ. Тогда мы будем иметь приближенные равенства: Подставляя полученные равенства в уравнение (91.4) и сокращая на общий множитель h, находим *) В линзах главная оптическая ось существенно отличается от побочных тем, что она есть единственная ось, проходящая через центры обеих сферических поверхностей, ограничивающих линзу. То, что высота h, равно как и угол , не входят в окончательный результат, означает, что любой луч, выходящий из точки S (и принадлежащий к достаточно узкому пучку), после отражения пройдет через точку S' на расстоянии а' от полюса. Таким образом, точка S' есть изображение точки S. Мы видим, что при отражении в сферическом зеркале изображением точечного источника является снова точка. Как и в случае линзы, точка S, в которой расположен источник, и точка S', в которой находится изображение, сопряжены между собой, т. е., поместив источник в точку S', мы получим изображение в точке S (следствие закона обратимости световых лучей, см. § 82). Полученная нами формула (91.6) является основной формулой сферического зеркала. Легко доказать, что для выпуклого сферического зеркала формула (91.6) остается в силе. 43. Построение изображения в зеркалах. Фокус и фокусное расстояние сферического зеркала. Найдем положение фокуса Fсферического зеркала, т. е. точки, в которой пересекутся после отражения в подобном зеркале лучи, параллельные его главной оси. Как мы знаем, для получения параллельного пучка лучей источник нужно удалить весьма далеко, т. е. [положить в формуле (91.6) 1/а=0. В этом случае a'=fесть фокусное расстояние зеркала. Для величины фокусного расстояния, пользуясь формулой (91.6), находим Соединяя формулы (91.6) и (92.1), получим формулу зеркала в виде т. e. в виде, аналогичном формуле (89.6) тонкой линзы. В случае вогнутого зеркала фокус расположен на середине расстояния между полюсом и центром сле- 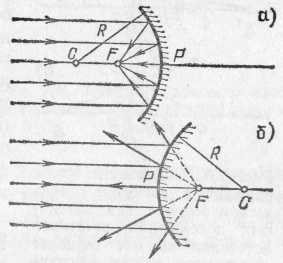 Рис. 206. Фокусы сферических зеркал: а) вогнутое зеркало; б) выпуклое зеркало. (Лучи показаны падающими на значительную часть сферических зеркал. Их следует представлять себе пересекающими зеркало на малой высоте от оси, т. е. захватывающими малую часть зеркала.) ва от полюса (рис. 206, а); в случае выпуклого зеркала фокус расположен на расстоянии R/2 справа от полюса, т .е. является мнимым (рис. 206, б). Пользуясь тем, что источник и его изображение находятся в сопряженных между собой точках, мы можем сразу сделать вывод, что если точечный источник света находится в фокусе зеркала, то его изображение находится в бесконечности, т. е. из зеркала выходит параллельный пучок лучей. Это условие служит основой для получения при помощи вогнутых зеркал параллельных световых пучков, точнее, пучков, близких к параллельным. О применении этого условия к устройству прожекторов мы уже говорили в гл. VIII *). Заметим, что при рассмотрении свойств сферического зеркала, как и в случае линзы, мы предполагали, во-первых, что используется очень узкий пучок лучей, прилегающих к оси зеркала, и, во-вторых, что применяется точечный источник света. Оба эти требования, конечно, вполне строго выполнены быть не могут. Вопрос о том, насколько существенны отступления от этих требований, в каждой конкретной задаче должен решаться особо. 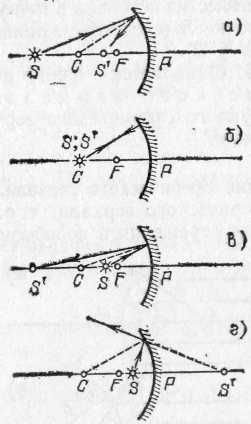 Рис. 207. Образование изображения в вогнутом сферическом зеркале при различных положениях точечного источника на оси зеркала: о) источник между центром и бесконечностью; б) в центре; в) между центром и фокусом; г) между фокусом и зеркалом |
